اندازه لبگ در نظریه اندازه | به زبان ساده

یکی از مفاهیم اصلی در ریاضیات مدرن و امروزی، «اندازه» (Measure) و در پس آن «نظریه اندازه» (Measure Theory) است. در نظریه اندازه، انتگرال، مشتق و دیگر مفاهیم اولیه حساب دیفرانسیل و انتگرال، توسعه یافته و برای توابع مجموعه‌ای (Set Functions) مجدد تعریف شدند. تعاریف جدید البته با قضیه‌های قبلی در حسابان نیز مطابقت داشته ولی امکان به کارگیری آن‌ها را در فضاهای دیگر، مانند «فضای باناخ» (Banach Space) و «فضای هیلبرت» (Hilbert Space)، فراهم می‌آورد. در این نوشتار به یکی از شیوه‌های کاربردی و البته محبوب تعیین اندازه برای مجموعه‌ها به نام اندازه لبگ در نظریه اندازه می‌پردازیم. البته به کارگیری «اندازه لبگ» (Lebesgue Measure) در بسیاری از قضیه‌ها و مفاهیم دیگر حسابان نیز به کار گرفته می‌شود که نشان از اهمیت تعریف این اندازه دارد.

به منظور آشنایی بیشتر با مفاهیم اولیه در نظریه اندازه بهتر است نوشتارهایی دیگر مجله فرادرس مانند نظریه اندازه در ریاضیات — مفاهیم و کاربردها و فضای متریک و نامساوی مثلثی — به زبان ساده را مطالعه کنید. همچنین خواندن مطالب قضیه تفکیک لبگ در نظریه اندازه — به زبان ساده و تجزیه هان و کاربردهای آن — به زبان ساده نیز خالی از لطف نیست.

اندازه لبگ در نظریه اندازه

در نظریه اندازه که شاخه‌ای از ریاضیات مدرن محسوب می‌شود، اندازه لبگ که توسط ریاضیدان فرانسوی، «هنری لبگ» (Henry Lebesgue) معرفی شده، یک روش استاندارد برای اندازه‌گیری روی مجموعه‌ها در «فضای اقلیدسی» (Euclidean Space) با $$n$$ بُعد، محسوب می‌شود. هنری لبگ، اندازه مورد نظرش را در سال ۱۹۰۱ معرفی و طی مقالاتی مرتبط با انتگرال لبگ کرد. در پایان‌نامه دکتری خود نیز از هر دو مفهوم بهره گرفت و در سال ۱۹۰۲ در مقطع دکتری، فارغ‌التحصیل شد.

در فضای اقلیدسی، در حالتی که ابعاد $$n=1$$ باشد، این اندازه با طول و زمانی که $$n=2$$ باشد، اندازه لبگ به مانند اندازه سطح عمل می‌کند. همچنین برای $$n=3$$ در فضای اقلیدسی، اندازه لبگ همان حجم در این فضا تلقی می‌شود. معمولا در زمانی که $$n$$ بزرگتر از ۲ باشد واژه حجم را برای اندازه لبگ در فضای اقلیدسی به کار می‌برند.

نکته: مجموعه‌هایی که اندازه لبگ روی آن‌ها قابل اجرا یا محاسبه است، مجموعه‌های «اندازه‌پذیر لبگ» (Lebesgue-measurable) یا «لبگ-اندازه‌پذیر» نامیده می‌شوند.

اهمیت اندازه لبگ در آنالیز حقیقی است که در آنجا، «انتگرال لبگ» (Lebesgue Integration) تعریف و به کار برده می‌شود. اندازه لبگ برای مجموعه $$E$$ را معمولا به صورت $$\lambda(E)$$ نشان می‌دهند.

تعریف اندازه لبگ

فرض کنید که مجموعه $$E$$ که زیر مجموعه‌ای از اعداد حقیقی است را به صورت یک فاصله مانند $$I=[a,b]$$ نشان دهیم (البته این فاصله می‌تواند به صورت $$I=(a,b)$$ نیز باشد). در این صورت «اندازه خارجی لبگ» (Lebesgue outer measure) با نماد $$\lambda^*$$، به شکل زیر حاصل می‌شود.

$$\large {\displaystyle \lambda ^{*}(E) = \operatorname {inf} \left\{\sum _{k = 1}^{\infty }\ell (I_{k}):{(I_{k})_{k\in \mathbb {N} }}{\text{ is a sequence of open intervals with }}E\subseteq \bigcup _{k=1}^{\infty }I_{k}\right\}}$$

رابطه بالا نشان می‌دهد که اگر $$E$$ زیر مجموعه‌ای از همه فاصله‌های باز در اعداد حقیقی باشد، آنگاه اندازه خارجی لبگ برابر است بزرگترین کران پایین (Inf) مجموع طول این فاصله‌ها. اندازه لبگ روی سیگما-میدان لبگ قابل تعریف است. این سیگما میدان از مجموعه‌هایی مثل $$E$$ تشکیل شده است که در شرط زیر صدق کنند.

$$\large \lambda^*(A) = \lambda^*(A \cap E) + \lambda^*(A \cap E^c) , \;\; A \subseteq R$$

توجه داشته باشید که مجموعه $$A$$ زیر مجموعه اعداد حقیقی در نظر گرفته شده است. به این ترتیب در سیگما-میدان لبگ، اندازه لبگ هر مجموعه با اندازه خارجی لبگ برابر خواهد شد.

$$\large \lambda(E) = \lambda^*(E)$$

مجموعه‌هایی که متعلق به سیگما-میدان لبگ نباشند، اندازه لبگ برایشان تعریف نشده و اندازه‌پذیر لبگ محسوب نمی‌شوند. توجه داشته باشید که چنین مجموعه‌ای وجود دارد. برای مثال می‌توان به «مجموعه ویتالی» (Vitali Sets) اشاره کرد. بنابراین سیگما میدان لبگ باید حتما شامل مجموعه توانی (Power Set) اعداد حقیقی ($$R$$) باشد.

بهتر است مفهوم اندازه لبگ و نقش آن را در ریاضیات بازتر کنیم.

مفهوم اندازه لبگ

بخش اول تعریفی که در ابتدای متن بیان شد، نشان می‌دهد که زیر مجموعه $${ \displaystyle E}$$ از اعداد حقیقی با پوشش دادن مجموعه‌های فواصل باز، به اندازه خارجی خود کاهش می‌یابند. هر یک از این مجموعه فواصل مثل $${\displaystyle I}$$ مجموعه $$\displaystyle {E}$$ را تحت پوشش قرار می‌دهند، به این معنا که وقتی فواصل با یکدیگر جمع می‌شوند (اجتماع آن‌ها حاصل می‌آید)، کل مجموعه $${\displaystyle E}$$ را می‌سازند. طول کل هر کدام از پوشش‌ها می‌تواند بیش‌برآوردی از اندازه لبگ برای مجموعه $$E$$ باشد، زیرا $${\displaystyle E}$$ زیرمجموعه‌ای از فواصل است و بنابراین فواصل ممکن است شامل نقاطی باشند که در مجموعه $${\displaystyle E}$$ حضور ندارند.

فیلم آموزش فرایندهای تصادفی یا اتفاقی Stochastic Processes در فرادرس

کلیک کنید

اندازه بیرونی لبگ به عنوان بزرگترین کران پایین (inf) طولی از بین کلیه مجموعه‌های ممکن (فاصله‌های پوشش دهنده) است. به این ترتیب اندازه بیرونی لبگ همان طول کل فواصل یا مجموعه‌های بازه‌ای است که $$E$$ را به طور فشرده و بدون هیچ اشتراکی، می‌پوشاند.

چیزی که تا اینجا مشخص شد، اندازه بیرونی لبگ بود. این که آیا اندازه خارجی لبگ را می‌توان اندازه لبگ در نظر گرفت احتیاج به یک شرط اضافه دارد. این شرط با در نظر گرفتن زیر مجموعه‌های $${\displaystyle A}$$ از اعداد حقیقی و با استفاده از $${\displaystyle E}$$ به عنوان ابزاری برای افراز (Partitioning) یا تقسیم $${\displaystyle A}$$ به دو بخش یا مجموعه مورد بررسی قرار می‌گیرد. این بخش‌ به صورت زیر تعریف می‌شود.

بخشی از $${\displaystyle A}$$ که با $${\displaystyle E}$$ اشتراک دارد و باقی مجموعه $${\displaystyle A}$$ که عضوی در $${\displaystyle E}$$ ندارد که می‌توان آن را همان تفاضل مجموعه‌های $$A$$ و $$E$$ یعنی ($$A- E$$) در نظر گرفت. این دو بخش از مجموعه $${\displaystyle A}$$، مرتبط با اندازه بیرونی لبگ هستند. اگر برای هر زیرمجموعه از اعداد حقیقی مثل $${\displaystyle A}$$، بخش $${\displaystyle A-E}$$، اندازه بیرونی لبگ داشته باشد، آنگاه اندازه بیرونی $$E$$ همان اندازه لبگ برای $$E$$ خواهد بود.

خصوصیات اندازه لبگ

اندازه لبگ روی فضای $$n$$ بُعدی از اعداد حقیقی ($$R^n$$) دارای خواص زیر است:

1. اگر A حاصل «ضرب دکارتی» (Cartesian Product) فواصل $$I_1 \times I_2 \times \ldots \times I_n$$ باشد، آنگاه $$A$$ می‌تواند لبگ-اندازه‌پذیر بوده و اندازه آن برابر با $${\displaystyle \lambda (A) = | I_1 | \cdot | I_2 | \cdots | I_n |}$$ خواهد بود. توجه داشته باشید که در اینجا، $$| I |$$ بیانگر طول بازه $$I$$ است.
2. اگر مجموعه $$\displaystyle A$$ حاصل اجتماع مجموعه‌های شمارش‌پذیر جدا از هم و اندازه‌پذیر لبگ باشد، آنگاه $$A$$ نیز اندازه‌پذیر لبگ بوده و اندازه لبگ آن از طریق مجموع (یک دنباله نامتناهی) از اندازه‌های لبگ این مجموعه‌ها، قابل محاسبه است.
3. اگر مجموعه $$\displaystyle A$$ اندازه‌پذیر لبگ باشد، مکمل آن نیز اندازه‌پذیر لبگ خواهد بود.
4. اندازه لبگ برای هر مجموعه لبگ-اندازه‌پذیر، نامنفی است. یعنی برای هر مجموعه لبگ-اندازه‌پذیر $$A$$ داریم $$\lambda(A) \geq 0$$.
5. اگر $$\displaystyle A , B$$، دو مجموعه اندازه پذیر لبگ باشند و همچنین مجموعه $$A$$ زیر مجموعه $$B$$ باشد، آنگاه اندازه لبگ $$A$$ نیز کوچکتر یا مساوی با اندازه لبگ مجموعه $$B$$ خواهد بود. به این معنی که $$\displaystyle A \subset B \rightarrow \lambda (A) \leq \lambda(B)$$. این خاصیت با توجه به خصوصیات ۲ و ۳ و ۴، حاصل می‌شود.
6. اجتماع و اشتراک تعداد مشخصی از مجموعه‌های لبگ-اندازه‌پذیر، باز هم لبگ-اندازه‌پذیر خواهد بود. توجه داشته باشید که این رابطه را نمی‌توان از خاصیت‌های 2 و 3 نتیجه گرفت، زیرا می‌توان خانواده‌ای از مجموعه‌های جدا از هم پیدا کرد که تحت عمل متمم‌گیری و اجتماع قابل شمارش، بسته بوده ولی تحت اجتماع شمارش‌پذیر بسته نباشد. برای مثال می‌توانید کلاس تشکیل شده از مجموعه‌های $${\displaystyle \{\emptyset ، \{ 1،2،3،4 \} ، \{1،2 \} ، \{3،4 \} ، \{1،3 \} ، \{2،4 \} \} \ }$$ را در نظر بگیرید.
7. اگر $$A$$ زیرمجموعه باز یا بسته از $$R^n$$ (یا حتی مجموعه بورل) باشد، می‌توان نتیجه گرفت که $$A$$، اندازه‌پذیر لبگ است.
8. اگر $$A$$ مجموعه‌ای با اندازه لبگ باشد، با توجه به تعریف اندازه لبگ می‌توان آن را یک مجموعه «تقریبا باز» (Approximately Open) یا «تقریبا بسته» (Approximately Close) در نظر گرفت.
9. یک مجموعه با اندازه لبگ را می‌توان بین یک مجموعه باز و یک مجموعه بسته، «فشرده» (Squeeze) کرد. این ویژگی معمولا به عنوان تعریف جایگزین برای اندازه لبگ مورد استفاده قرار می‌گیرد. به طور دقیق‌تر، $${\displaystyle E \subset \mathbb {R}}$$، لبگ-اندازه‌پذیر است اگر و فقط اگر برای هر $${\displaystyle \varepsilon> 0}$$، یک مجموعه باز مثل $${\displaystyle G}$$  و یک مجموعه بسته $${\displaystyle F}$$ وجود داشته باشند به گونه‌ای که $${\displaystyle F\subset E\subset G}$$ و $${\displaystyle \lambda (G\setminus F)<\varepsilon }$$.
10. اندازه لبگ، هم به صورت «محلی متناهی» (Locally Finite) و هم یک «اندازه داخلی» (Inner Measure) است، بنابراین یک «اندازه رادون» (Radon Measure) محسوب می‌شود.
11. اندازه لبگ روی مجموعه‌های باز و ناتهی کاملاً مثبت است، بنابراین تکیه‌گاه یا دامنه این اندازه همه $$R^n$$ خواهد بود.
12. اگر $$A$$، مجموعه‌ای با اندازه لبگ برابر با صفر ($$\lambda(A) = 0$$) یا یک «مجموعه صفر» (Null Set) باشد، آنگاه هر زیر مجموعه از A نیز یک مجموعه صفر (با اندازه لبگ برابر با صفر) خواهد بود. همچنین می‌توان گفت که هر زیر مجموعه از $$A$$، اندازه‌پذیر لبگ است.
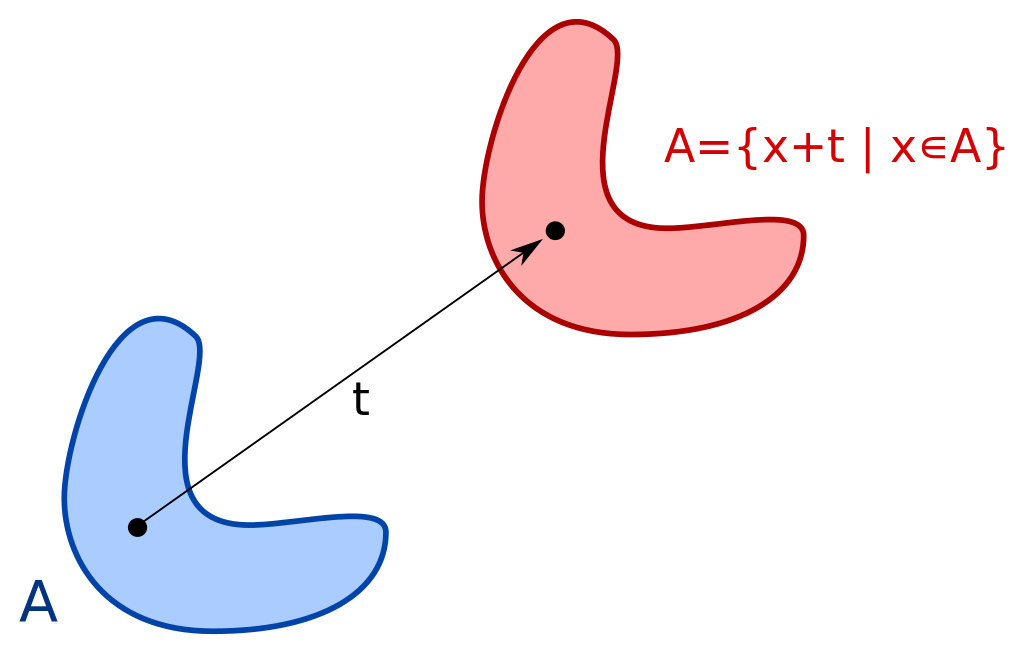
13. اگر مجموعه $$A$$، اندازه‌پذیر لبگ باشد و $$x$$ نیز عضوی از فضای $$n$$ بعدی اعداد حقیقی باشد ($$R^n$$)، آنگاه ترجمه $$A$$ توسط $$x$$، که به صورت $$A + x = {a + x: a ∈ A}$$ مشخص می‌شود، اندازه‌پذیر لبگ بوده و اندازه این ترجمه با اندازه $$A$$ برابر خواهد بود. به این ترتیب خواهیم داشت: $$\lambda(A+x) = \lambda(A)$$.
14. اگر مجموعه $$A$$ اندازه‌پذیر لبگ باشد و $$\delta$$ نیز عضوی از اعداد حقیقی، با فرض $${\displaystyle \delta> 0}$$، «انبساط» (dilation) یا توسیع $$\displaystyle A$$ توسط $$\displaystyle \delta$$ به شکل $$\displaystyle \delta A$$ مشخص شده و داریم $${\displaystyle \delta A=\{\delta x:x\in A\}}$$، بطوریکه $$\delta A$$، اندازه‌پذیر لبگ بوده و اندازه آن برابر است با $$\delta^n \lambda(A)$$.
15. به طور کلی، اگر $$T$$، یک تبدیل خطی و $$A$$ نیز زیر مجموعه لبگ-اندازه‌پذیر از $$R^n$$ باشد، آنگاه $$T(A)$$ نیز اندازه‌پذیر لبگ بوده و داریم $$\lambda(T(A)) = |\det(T)|\lambda(A)$$.

همه موارد فوق را به صورت خلاصه می‌توان به شرح زیر مشخص کرد.

مجموعه‌های اندازه‌پذیر لبگ، یک سیگما-میدان ($$\sigma \text{-Field}$$) را تشکیل می‌دهند که شامل همه حاصل ضرب‌های فواصل است و $$\lambda$$ یک اندازه کامل یکتا و ناوردا نسبت به ترجمه است. بطوری که:

$$\large {\displaystyle \lambda ([0,1] \times [0,1] \times \cdots \times [0,1]) = 1}$$

نکته: توجه داشته باشید که اندازه لبگ، یک اندازه با خاصیت سیگما-متناهی ($$\sigma\text{- finite}$$) است.

مجموعه صفر در اندازه لبگ

زیر مجموعه‌ای از $$R^n$$ مثل $$A$$، یک «مجموعه صفر» (Null Set) است، اگر برای هر $$\epsilon >0$$، بتوان $$A$$ را با تعداد زیادی از حاصل‌ضرب‌های فاصله‌ها پوشش (Covered) داد که حجم کل آن‌ها، حداکثر $$\epsilon$$ باشد. طبق اندازه لبگ، تمام مجموعه‌های شمارش‌پذیر، مجموعه صفر (Null Set) هستند (البته برحسب اندازه لبگ).

اگر زیر مجموعه ای از $$R^n$$ دارای «بُعد هاسدورف» (Hausdorff Dimension) کمتر از n باشد، یک مجموعه صفر با توجه به اندازه لبگ با بُعد $$n$$ حاصل می شود. در اینجا بُعد هاسدورف، نسبت به «فضای متریک اقلیدسی» (Euclidean Metric Space) روی $$R^n$$ در نظر گرفته شده است. از طرف دیگر، یک مجموعه ممکن است دارای ابعاد توپولوژیکی کمتر از $$n$$ بوده ولی دارای اندازه لبگ مثبت باشد.

برای آنکه نشان دهیم مجموعه $$A$$، لبگ-اندازه‌پذیر است، می‌توان هدف را پیدا کردن مجموعه‌ای بهتر مانند $$B$$ در نظر گرفت که اختلاف $$A$$ و $$B$$ فقط در یک مجموعه صفر باشد. به این ترتیب با توجه به تفاضل متقارن $$(A-B) \cup (B-A) = \text{Null set}$$. بنابراین اگر $$B$$، یک مجموعه متشکل از اجتماع و اشتراک متناهی از مجموعه‌های دیگر باشد، آنگاه $$A$$ نیز اندازه-پذیر لبگ خواهد بود.

ساختار اندازه لبگ

ساختار مدرن برای اندازه لبگ، برگرفته از کاربرد قضیه «توسیع کاراتئودُری» (Caratheodory's Extension Theorem) است. نحوه عملکرد به شرح زیر است.

• با در نظر گرفتن $$n \in N$$ به شکل ثابت،  یک جعبه در $$R^n$$ را به صورت زیر تشکیل می‌دهیم که در آن $$a_i \leq b_i$$ بوده و نماد حاصل‌ضرب ($$\prod$$) نشانگر «ضرب دکارتی» (Cartesian Product) است.

$$\large B=\prod_{i=1}^n [a_i,b_i] \, ,$$

• حجم چنین جعبه‌ای، به صورت زیر تعریف می‌شود.

$$\large\operatorname{vol}(B)=\prod_{i=1}^n (b_i-a_i) \,$$

• برای هر زیرمجموعه از $$R^n$$ مثل $$A$$، می‌توان ضرب خارجی $$\lambda^*(A)$$ را به شکل زیر تعریف کرد. که در آن $$C$$، مجموعه‌ای شمارش‌پذیر از جعبه‌ها است که اجتماع آن‌ها مجموعه $$A$$ را می‌پوشاند.

$$\large {\displaystyle \lambda ^{*}(A)=\inf \left\{\sum _{B\in {\mathcal {C}}}\operatorname {vol} (B):{\mathcal {C}}\right\}.}$$

• مجموعه $$A$$ را اندازه‌پذیر لبگ می‌نامیم اگر برای هر زیر مجموعه‌ای مثل $$S$$ از $$R^n$$ رابطه زیر برقرار باشد.

$$\large \lambda^*(S) = \lambda^*(S \cap A) + \lambda^*(S \setminus A) \,$$

مجموعه‌های اندازه‌پذیر لبگ معرفی شده یک سیگما میدان تشکیل داده و اندازه لبگ برای مجموعه $$A$$ به صورت $$\lambda(A) = \lambda^*(A)$$ برای هر مجموعه اندازه‌پذیر لبگ، تعریف می‌شود.

وجود مجموعه‌هایی که لبگ-اندازه‌پذیر نیستند، پیامد یک اصل بدیهی در نظری مجموعه است که به «اصل انتخاب» (Axiom of Choice) شهرت دارد و نسبت به اصول دیگر در نظریه مجموعه‌ها، بسیار متفاوت است.

«قضیه ویتالی» (Vitali Theorem) که از اصل انتخاب نتیجه می‌شود، نشان می‌دهد که زیر مجموعه‌های اعداد حقیقی ($$R$$)، وجود دارند که اندازه‌پذیر لبگ نیستند. با فرض اصل موضوع انتخاب، مجموعه‌های اندازه ناپذیر لبگ، پدید می‌آیند که خواص تعجب‌آوری مانند «پارادوکس باناخ-تارکسی» (Banach-Tarski Paradox) را پدید می‌آورند.

در سال 1970، «روبرت سولووی» (Robert M. Solovay) نشان داد كه وجود مجموعه‌هایی اندازه‌ناپذیر لبگ، در چارچوب نظریه مجموعه «زرملو-فرانکل» (Zermelo-Fraenkel) بدون در نظر گرفتن اصل انتخاب امکان‌پذیر نیست.

مثال‌هایی از اندازه لبگ

هر فاصله باز یا بسته $$[a, b]$$ از اعداد حقیقی اندازه‌پذیر لبگ است. اندازه چنین بازه‌هایی برابر با طول آن بازه یعنی $$b - a$$ خواهد بود. این مقدار با اندازه لبگ برای فاصله باز $$(a, b)$$ نیز یکسان است، زیرا تفاوت بین دو مجموعه فقط شامل نقاط انتهایی یعنی $$a$$ و $$b$$ است که اندازه لبگ برای این نقطه‌ها برابر با صفر است. در حقیقت مجموعه‌های شمارش‌پذیر دارای اندازه لبگ صفر هستند.

فیلم آموزش مبانی آنالیز ریاضی – جامع و کاربردی در فرادرس

کلیک کنید

هر حاصل ضرب دکارتی تشکیل شده از فواصل $$[a, b]$$ و $$[c, d]$$ اندازه‌پذیر لبگ است و اندازه لبگ آن برابر است با حاصل ضرب $$(b - a)$$ در $$(d - c)$$، یعنی مساحت مستطیل مربوطه این بازه‌ها همان اندازه لبگ خواهد بود.

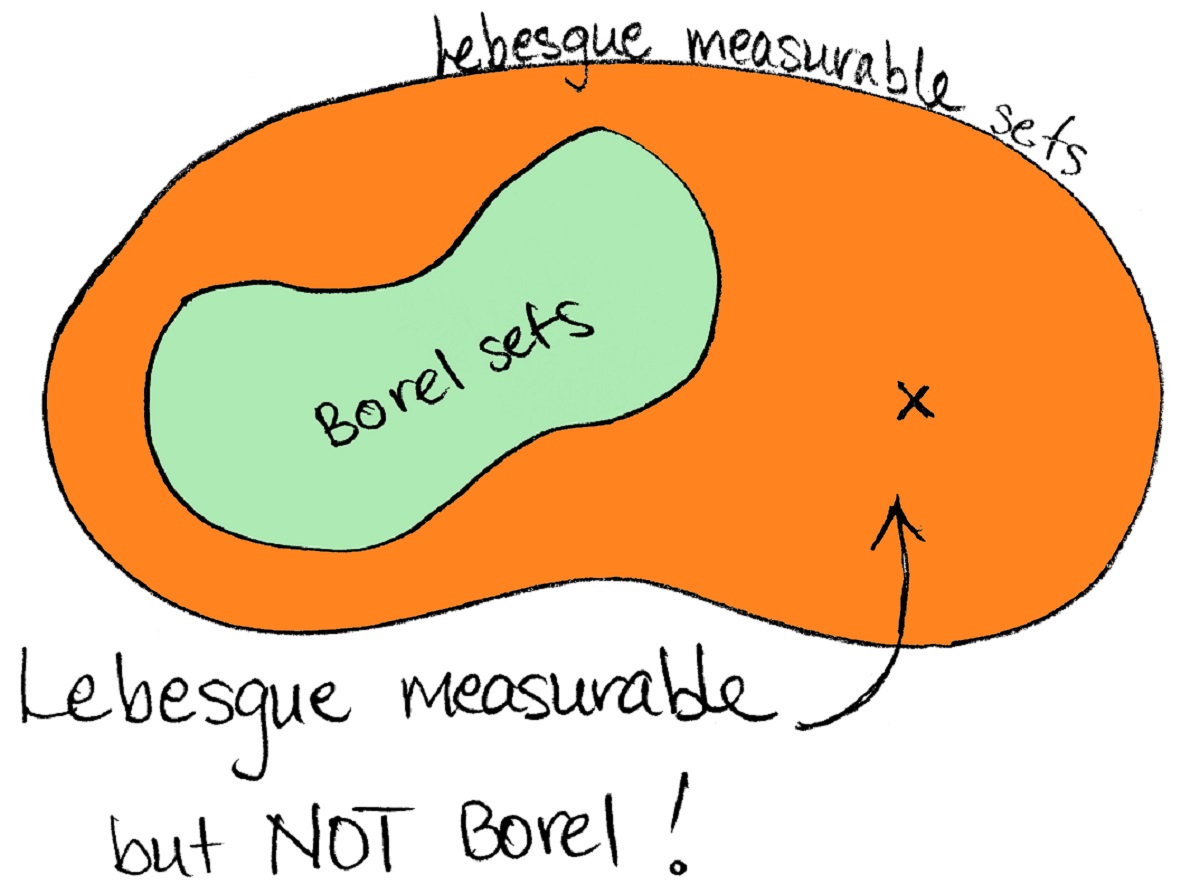
علاوه بر این، هر مجموعه بورل، اندازه‌پذیر لبگ است. با این حال، مجموعه‌هایی اندازه‌پذیر لبگ وجود دارند که مجموعه‌های بورل نیستند.

هر مجموعه شمارش‌پذیر از اعداد حقیقی، دارای اندازه لبگ صفر است. به طور خاص، اندازه لبگ مجموعه اعداد جبری (طبیعی یا صحیح) صفر خواهد بود. حتی اگر این مجموعه در R، «چگال» (Dense) باشد.

«مجموعه کانتور» (Cantor Set) و مجموعه «اعداد لیوویل» (Liouville Numbers) نمونه‌هایی از مجموعه‌های غیر قابل شمارش هستند که اندازه لبگ برابر با صفر دارند.

«مجموعه‌های ویتالی» (Vitali sets) نمونه‌هایی از مجموعه‌هایی هستند که با توجه به اندازه لبگ، اندازه‌پذیر نیستند. وجود آنها متکی به «اصل انتخاب» (Axiom of Choice) است.

«منحنی‌های اسگود» (Osgood Curves) منحنی های مسطح و ساده‌ای هستند که اندازه لبگ روی آن‌ها مثبت است. چنین منحنی‌هایی را می‌توان به کمی تغییرات روی منحنی‌های پیانو (Peano Curves) ایجاد کرد. منحنی اژدها (Dragon Curve) نمونه غیرمعمول در این زمینه است.

هر خطی در $${\displaystyle \mathbb {R}^{n}}$$، برای $${\displaystyle n \geq 2}$$، دارای اندازه لبگ صفر است. به طور کلی، هر صفحه چند بُعدی در فضای محیط خود دارای اندازه لبگ صفر است.

ارتباط اندازه لبگ با اندازه‌های دیگر

«اندازه بورل» (Borel measure) با «اندازه لبگ» (Lebesgue Measure) در مجموعه‌هایی که برای هر دو آن‌ها اندازه‌پذیر باشند، مقدار یکسانی دارد. البته باید توجه داشت که تعداد مجموعه‌های اندازه‌پذیر لبگ بسیار بیشتر از مجموعه‌ها اندازه‌پذیر بورل است. اندازه بورل در حقیقت یک «ترجمه ناوردا» (Invariant Translation) است، ولی «کامل» (Complete) نیست.

فیلم مجموعه آموزش آمار و احتمالات – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

«اندازه هار» (Haar Measure) را می‌توان در هر گروه فشره محلی تعریف کرد. چنین اندازه‌ای، تعمیم اندازه لبگ در نظر گرفته می‌شود. «اندازه هاسدروف» (Hausdorff Measure)، نیز یک تعمیم روی اندازه لبگ خواهد بود. بطوری که برای تعیین اندازه زیر مجموعه‌های فضای $$R^n$$ مناسب که در ابعاد کوچکتر از $$n$$ هستند، به کار می‌رود. برای مثال، سطوح یا منحنی‌ها فضای سه بُعدی، همچنین «فراکتال‌ها» (Fractal)، اندازه‌پذیر هاسدورف هستند.

خلاصه و جمع‌بندی

در این نوشتار با اندازه لبگ در ریاضیات آشنا شدیم. همچنین خصوصیات و اصطلاحاتی که برای مجموعه‌های اندازه‌پذیر لبگ وجود دارد نیز مورد بحث قرار گرفت. با توجه به نزدیکی نظریه احتمال و نظریه اندازه، این حوزه از ریاضیات بخصوص برای کسانی که با آمار و احتمالات سروکار دارند، جالب بوده و مبانی نظریه احتمال را برایشان بوسیله نظریه اندازه در ریاضیات روشن‌تر می‌کند. از طرفی اندازه لبگ با انتگرال لبگ نیز در رابطه است. همین موضوع می‌تواند مشوقی برای آشنایی بیشتر با این اندازه پر کاربرد در ریاضیات باشد.