اصل آرگومان — از صفر تا صد

۱۴۹۸ بازدید

آخرین به‌روزرسانی: ۱۳ اردیبهشت ۱۴۰۲

زمان مطالعه: ۱۷ دقیقه

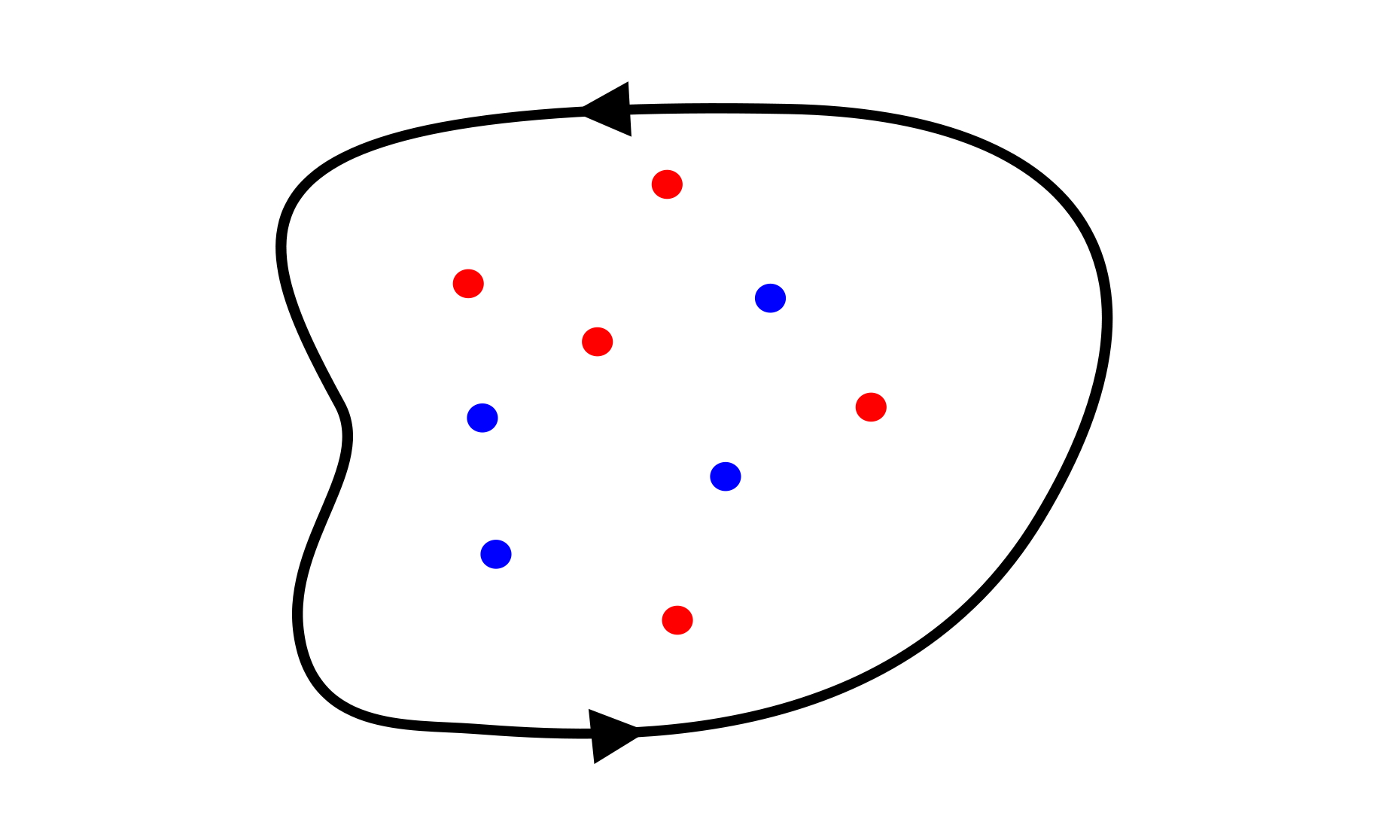
اصل آرگومان نتیجه قضیه مانده‌ها است. این قضیه تعداد دور یک منحنی را با تعداد صفرها و قطب‌های درون آن مرتبط می‌کند. اصل آرگومان کاربردهای زیادی دارد و در مواقعی که بخواهیم مکان صفرها و قطب‌ها را بدانیم، بسیار کارساز خواهد بود.

فهرست مطالب این نوشته

اصل آرگومان

برای بیان اصل آرگومان، ابتدا چند فرض را در نظر می‌گیریم:

$$ \gamma $$ یک منحنی بسته ساده است و در جهت خلاف عقربه‌های ساعت (پادساعتگرد) چرخیده است.
$$ f ( z ) $$ درون $$ \gamma $$ تحلیلی است، به جز (احتمالاً) تعداد محدودی قطب درون (و نه روی) $$ \gamma$$ و تعداد محدودی صفر درون (و نه روی) $$ \gamma$$.
فرض می‌کنیم $$ p _ 1 $$، ... و $$ p _ m $$ قطب‌های تابع $$ f $$ درون منحنی $$ \gamma $$ هستند.
فرض می‌کنیم $$ z _ 1 $$، ... و $$ z _ n $$ صفرهای تابع $$ f $$ درون منحنی $$ \gamma $$ هستند.
$$ \operatorname {mult} \left ( z _ { k } \right ) $$ را به عنوان تعداد صفرها در $$ z _ k $$ و $$ \operatorname {mult} \left ( p _ { k } \right ) $$ را به عنوان تعداد قطب‌ها در $$ p _ k $$ در نظر می‌گیریم.

ابتدا یک قضیه را بیان می‌کنیم که منجر به اصل آرگومان می‌شود.

فیلم آموزش ریاضی مهندسی در فرادرس

کلیک کنید

قضیه ۱: با توجه به فرضیات بالا، داریم:

$$ \large \int _ { \gamma } \frac { f ^ { \prime } ( z ) }{ f ( z ) } d z = 2 \pi i \left ( \sum \operatorname {mult} \left ( z _ { k } \right ) - \sum \operatorname {mult} \left ( p _ { k } \right ) \right ) $$

اثبات: برای اثبات این قضیه لازم است قطب‌ها و باقیمانده‌های $$ f' ( z )/ f ( z ) $$ را بدانیم. با در نظر گرفتن این موضوع، فرض کنید $$ f ( z ) $$ یک صفر مرتبه $$ m $$ در $$ z _ 0 $$ داشته باشد. سری تیلور $$ f ( z ) $$ حول $$ z _ 0 $$ به صورت زیر است:

$$ \large f ( z ) = ( z - z _ 0 ) ^ m g ( z ) $$

که در آن، $$ g ( z ) $$ یک تابع تحلیلی است و در همسایگی کوچک $$ z _ 0 $$ هیچگاه صفر نمی‌شود. در نتیجه، داریم:

$$ \large \begin {aligned}
\frac { f ^ { \prime } ( z ) } { f ( z ) } & = \frac { m \left ( z - z _ { 0 } \right ) ^ { m - 1 } g ( z ) + \left ( z -z _ { 0 } \right ) ^ { m } g ^ { \prime } ( z ) } { \left ( z -z _ { 0 } \right ) ^ { m } g ( z ) } \\
& = \frac { m } { z - z _ { 0 } } + \frac { g ^ { \prime }( z ) } { g ( z ) }
\end {aligned} $$

از آنجا که $$ g ( z ) $$ هیچگاه صفر نمی‌شود، $$ g' ( z ) / g ( z ) $$ در همسایگی $$ z _ 0 $$ تحلیلی است. این یعنی $$ z _ 0 $$ یک قطب ساده برای $$ f' (z ) / f ( z ) $$ است و داریم:

$$ \large \operatorname {Res} \left ( \frac { f ^ { \prime } ( z ) } { f ( z ) } , z _ { 0 } \right ) = m = \operatorname {mult} \left ( z _ { 0 } \right ) .$$

به طور مشابه، اگر $$ z _ 0 $$ قطبی از مرتبه $$ m $$ باشد، آنگاه سری لوران $$ f ( z ) $$ حول $$ z _ 0 $$ به شکل زیر است:‌

$$ \large f ( z ) = ( z - z _ 0 ) ^ { - m } g ( z ) $$

که در آن، $$ g ( z ) $$ تحلیلی است و در همسایگی کوچک $$ z _ 0 $$ هیچگاه صفر نمی‌شود. بنابراین:

$$ \large \begin {aligned}
\frac { f ^ { \prime } ( z ) } { f ( z ) } & = - \frac { m \left ( z - z _ { 0 } \right ) ^ { - m - 1 } g ( z ) + \left ( z - z _ { 0 } \right ) ^ { - m } g ^ { \prime } ( z ) } { \left ( z -z _ { 0 } \right ) ^ { - m } g ( z ) } \\
& = - \frac { m } { z - z _ { 0 } } + \frac { g ^ { \prime }( z ) } { g ( z ) }
\end {aligned} $$

مجدداً $$ z _ 0 $$ یک قطب ساده برای $$ f' ( z ) / f ( z ) $$ است و داریم:

$$ \large \operatorname {Res} \left ( \frac { f ^ { \prime } ( z ) }{ f ( z ) } , z _ { 0 } \right ) = - m = - \operatorname {mult} \left ( z _ { 0 } \right ) $$

بنابراین، طبق قضیه مانده‌ها، خواهیم داشت:

$$ \large \int _ { \gamma } \frac { f ^ { \prime } ( z ) } { f ( z ) } d z
= 2 \pi i \left ( \sum \operatorname {mult} \left ( z _ { k } \right ) - \sum \operatorname {mult} \left ( p _ { k } \right ) \right ) $$

تعریف: $$ Z _ { f , \gamma} $$ را به عنوان مجموع تعداد صفرهای $$ f $$ درون $$ \gamma $$ تعریف می‌کنیم. به طور مشابه $$ P _ { f , \gamma} $$ را مجموع تعداد قطب‌های $$ f $$ درون $$ \gamma $$ می‌نامیم. بنابراین، طبق قضیه ۱، داریم:

$$ \large \int _ { \gamma } \frac { f ^ { \prime } } { f } d z = 2 \pi i \left ( Z _ { f , \gamma } - P _ { f , \gamma } \right ) \quad \quad \quad ( 1 ) $$

تعریف: تعداد دور را با فرمول کوشی بیان می‌کنیم. اگر $$ \gamma $$ یک منحنی بسته باشد، آنگاه تعداد (یا شاخص) دور حول $$ z _ 0 $$ به صورت زیر تعریف می‌شود:

$$ \large \operatorname {nd} \left ( \gamma , z _ { 0 } \right ) = \frac { 1 } { 2 \pi i } \int _ { \gamma } \frac { 1 } { z - z _ { 0 } } d z $$

تصویر منحنی‌ها ($$ \Large f \circ \gamma $$)

یکی از نمادگذاری‌های اساسی در این آموزش، تصویر یک منحنی به منحنی دیگر است. یعنی، اگر $$ z = \gamma ( t) $$ یک منحنی و $$ w = f ( z ) $$ یک تابع باشد، آنگاه $$ w = f \circ \gamma ( t) = f (\gamma ( t)) $$ یک منحنی دیگر است. در این حالت، می‌گوییم $$ f $$ منحنی $$ \gamma $$ را به $$ f \circ \gamma $$ تصویر می‌کند. این موضوع در اصل آرگومان بسیار مهم است. به همین دلیل، برای یادگیری بهتر آن، چند مثال را بررسی می‌کنیم.

مثال ۱: $$ \gamma ( t) = e ^ { i t } $$ را با $$ 0 \le t \le 2 \pi $$ (دایره واحد) در نظر بگیرید. همچنین $$ f ( z ) = z ^ 2 $$ است. منحنی $$ f \circ \gamma $$ را توصیف کنید.

حل: واضح است که وقتی $$ t $$ از $$ 0 $$ تا $$ 2 \pi $$ تغییر می‌کند، $$ f \circ \gamma ( t) = e ^ { 2 i t } $$ دو بار دایره واحد را می‌پیماید.

مثال ۲: $$ \gamma ( t) = i t $$ را با $$ -\infty < t < \infty $$ (محور $$ y $$) در نظر بگیرید. با فرض $$ f( z ) = 1 / ( z + 1 ) $$، منحنی $$ f \circ \gamma $$ را توصیف کنید.

حل: $$ f ( z ) $$ یک تبدیل خطی کسری است و خط $$ \gamma $$ را به دایره گذرنده از مبدأ با مرکز $$ 1 / 2 $$ تصویر می‌کند. با بررسی چند نقطه، داریم:

$$ \large f ( - i ) = \frac { 1 } { - i + 1 } = \frac { 1 + i } { 2 } , \quad f ( 0 ) = 1 , \quad f ( i ) = \frac { 1 } { i + 1 } = \frac { 1 - i } { 2 } , \quad f ( \infty ) = 0 $$

می‌بینیم که وقتی $$ t $$ از $$ - \infty $$ تا $$ \infty $$ می‌رود، دایره در جهت عقربه‌های ساعت پیموده می‌شود.

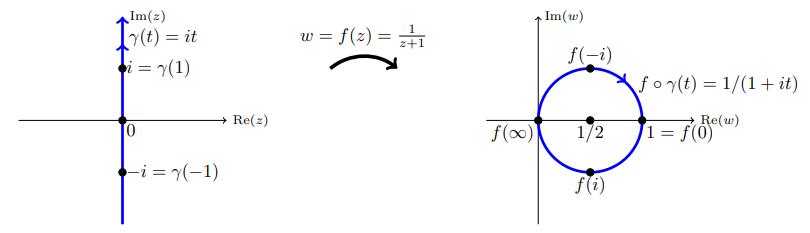
شکل ۱:‌ منحنی $$ z = \gamma ( t) = i t $$ به $$ w = f \circ \gamma ( t) = 1 / ( i t + 1 ) $$ تصویر شده است.

اصل آرگومان

با در نظر گرفتن مطالبی که تا اینجا ارائه کردیم، اکنون اصل آرگومان را در قالب یک قضیه بیان می‌کنیم.

قضیه ۲ (اصل آرگومان): طبق فرضیات و نمادگذاری‌های بالا، برای $$ f $$ و $$ \gamma $$ داریم:

$$ \large \int _ { \gamma } \frac { f ^ { \prime } ( z ) } { f ( z ) } d z = 2 \pi i \operatorname {Ind} ( f \circ \gamma , 0 ) = 2 \pi i \left ( Z _ { f , \gamma } - P _ { f , \gamma } \right ) \quad \quad ( 2 ) $$

اثبات: طبق قضیه ۱، داریم:

$$ \large \int _ { \gamma } \frac { f ^ { \prime } ( z ) } { f ( z ) } d z = 2 \pi i \left ( Z _ { f , \gamma } - P _ { f , \gamma } \right ) $$

بنابراین، لازم است نشان دهیم انتگرال نیز برابر تعداد دور داده شده است. این کار به سادگی با تغییر متغیر $$ w = f ( z ) $$ قابل انجام است. با این تغییر متغیر، کانتور $$ z = \gamma ( T) $$ به $$ w = f \circ \gamma ( t) $$ تبدیل شده و $$ d w = f' ( z ) d z $$ است. بنابراین:

$$ \large \int _ { \gamma } \frac { f ^ { \prime } ( z ) } { f ( z ) } d z = \int _ { f \circ \gamma } \frac { d w } { w } = 2 \pi i \operatorname {Ind} ( f \circ \gamma , 0 ) $$

تساوی آخر معادله بالا از تعریف تعداد دور به دست آمده است.

توجه کنید که طبق فرض، $$ \gamma $$ از صفرهای $$ f $$ عبور نمی‌کند، بنابراین، $$ w = f (\gamma ( t )) $$ هیچگاه صفر نخواهد شد و $$ 1 / w $$ در انتگرال مشکلی ایجاد نخواهد کرد.

اکنون یک نتیجه ساده برای اصل آرگومان بیان می‌کنیم که در ادامه مفید خواهد بود.

نتیجه: با فرض اینکه $$ f \circ \gamma $$ از $$ - 1 $$ عبور نکند، یعنی هیچ صفری از $$ 1 + f ( z ) $$ روی $$ \gamma $$ نباشد، داریم:

$$ \large \int _ { \gamma } \frac { f ^ { \prime } } { f + 1 } = 2 \pi i \operatorname {Ind} ( f \circ \gamma , - 1 ) = 2 \pi i \left ( Z _ { 1 + f , \gamma } - P _ { f , \gamma } \right ) \quad ( 3 ) $$

اثبات: با اعمال اصل آرگومان به معادله (۲) برای تابع $$ 1 + f ( z ) $$، داریم:

$$ \large \int _ { \gamma } \frac { ( 1 + f ) ^ { \prime } ( z ) } { 1 + f ( z ) } d z = 2 \pi i \operatorname {Ind} ( 1 + f \circ \gamma , 0 ) = 2 \pi i \left ( Z _ { 1 + f , \gamma } - P _ { 1 + f , \gamma } \right ) $$

اکنون می‌توانیم هر یک از جملات این معادله را با جملا متناظر در معادله (۳) مقایسه کنیم:

$$ \int _ { \gamma} \frac { ( 1 + f ) ^ { \prime } ( z ) } { 1 + f ( z ) } d z = \int _ { \gamma } \frac { f ^ { \prime } ( z ) }{ 1 + f ( z ) } d z $$ زیرا $$ ( 1 + f )' = f' $$
$$ \operatorname {Ind} ( 1 + f \circ \gamma , 0 ) = \operatorname {Ind} ( f \circ \gamma , - 1 ) $$ ($$ 1 + f $$ حول $$ 0$$ می‌چرخد، یعنی $$ f $$ حول $$ - 1$$ می‌چرخد).
$$ Z _ { 1 + f , \gamma } = Z _ { 1 + f , \gamma } $$ (مشابه در هر دو معادله)‌
$$ P _ { 1 + f , \gamma } = P _ { f , \gamma } $$ (قطب‌های $$ f $$، قطب‌های $$ 1 + f $$ هستند).

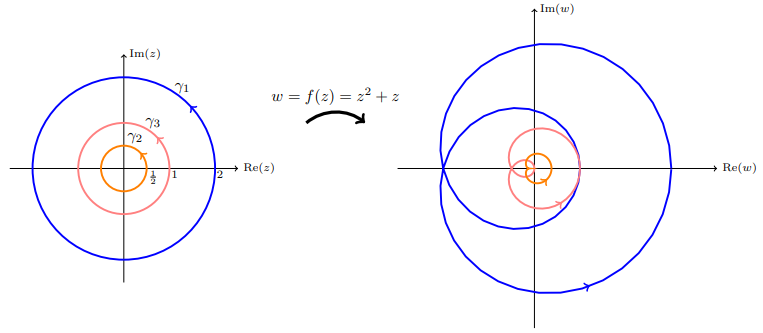
مثال ۳: با در نظر گرفتن $$ f ( z ) = z ^ 2 + z $$، تعداد دورهای $$ f \circ \gamma $$ را حول $$ 0 $$ برای هر یک از منحنی‌های زیر به دست آورید.

(الف) $$ \gamma _ 1 $$ = دایره‌ای به شعاع $$2$$.
(ب) $$ \gamma _ 2 $$ = دایره‌ای به شعاع $$1/2$$.
(پ) $$ \gamma _ 3 $$ = دایره‌ای به شعاع $$1$$.

حل: $$ f ( z ) $$ دو صفر در $$ 0 $$ و $$ - 1 $$ دارد و قطب ندارد. بنابراین، $$ f $$ در $$ \gamma _ 1 $$ قطبی ندارد و دارای دو صفر است. اصل آرگومان بیان می‌کند که $$ \mathrm{Ind}(f \circ \gamma _ 1 , 0 ) = Z _ { f , \gamma _ 1 } - P _ { f , \gamma _ 1 } = 2 $$. به طور مشابه، $$ f $$ در $$ \gamma _ 2 $$ قطبی ندارد و تنها دارای یک صفر است. بنابراین، $$ \mathrm{Ind}(f \circ \gamma _ 2, 0 ) = Z _ { f , \gamma _ 2 } - P _ { f , \gamma _ 2 } = 1-0=1 $$. برای $$ \gamma _ 3 $$، یک صفر $$ f $$ روی منحنی قرار دارد، یعنی $$ f ( - 1 ) = 0 $$، بنابراین، نمی‌توان از اصل آرگومان استفاده کرد. تصویر $$ \gamma _ 3 $$ در شکل زیر نشان داده شده است که از صفر می‌گذرد.

شکل ۲: تصویر سه دایره مختلف با $$ f ( z ) = z ^ 2 + z$$.

قضیه روشه

در این بخش،‌ قضیه روشه (Rouché's Theorem) را بیان می‌کنیم.

فیلم آموزش ریاضی مهندسی – مرور و حل سوالات کنکور دکتری در فرادرس

کلیک کنید

قضیه (قضیه روشه): فرضیات زیر را در نظر بگیرید:

$$ \gamma $$ یک منحنی بسته ساده است.
$$ f $$ و $$ h $$ توابعی تحلیلی روی $$ \gamma $$ و درون آن هستند، جز در تعداد محدودی قطب.
قطبی از $$ f $$ و $$ h $$ روی $$ \gamma $$ نیست.
نامساوی $$ | h | < | f | $$ روی $$ \gamma $$ برقرار است.

آنگاه:

$$ \large \begin {array} { c }
\text { Ind } ( f \circ \gamma , 0 ) = \operatorname {Ind} ( ( f + h ) \circ \gamma , 0 ) \\
\end {array} $$

یعنی:

$$ \large Z _ { f , \gamma } - P _ { f , \gamma } = Z _ { f + h , \gamma } - P _ { f + h , \gamma } \quad \quad ( 4 ) $$

اثبات: برای استفاده از اصل آرگومان باید تابعی داشته باشیم که صفر و قطبی روی $$ \gamma $$ نداشته باشد. بنابراین، ابتدا نشان می‌دهیم که این موضوع برای $$ f $$، $$ f + h $$ و $$ ( f + h ) / f $$ صحیح است. آرگومان به صورت زیر تغییر می‌کند:

صفرها: با توجه به $$ 0 \le |h|< | f | $$ روی $$ \gamma $$، بنابراین، $$ f $$ صفری روی $$ \gamma $$ ندارد. همچنین، $$ f + h $$ صفری روی $$ \gamma $$ ندارد، زیرا مقدار $$ h $$ هیچگاه به اندازه کافی بزرگ نخواهد بود که $$ f $$ را حذف کند. از آنجا که $$ f $$ و $$ f + h $$ صفر ندارند، $$ ( f + h ) / f $$ نیز صفر ندارد.
قطب‌ها: طبق فرض، $$ f $$ و $$ h $$ روی $$ \gamma $$ قطبی ندارند، بنابراین، $$ f + h $$ نیز روی $$ \gamma $$ قطبی نخواهد داشت. از آنجا که $$ f $$ روی $$ \gamma $$ صفری ندارد، $$ (f+ h ) / f $$ نیز روی آن قطبی نخواهد داشت.

اکنون می‌توانیم اصل آرگومان را به $$ f $$ و $$ f + h $$ اعمال کنیم:

$$ \large \begin {array} { c }
\frac { 1 } { 2 \pi i } \int _ { \gamma } \frac { f ^ { \prime } } { f } d z = \operatorname {Ind} ( f \circ \gamma , 0 ) = Z _ { f , \gamma } - P _ { f , \gamma } \quad \quad ( 5 ) \\
\frac { 1 } { 2 \pi i } \int _ { \gamma } \frac { ( f + h ) ^ { \prime } } { f + h } d z = \operatorname {Ind} ( ( f + h ) \circ \gamma , 0 ) = Z _ { f + h , \gamma } - P _ { f + h , \gamma} \quad ( 6 )
\end {array} $$

در ادامه، طبق فرض $$ \left | \frac { h } { f } \right | < 1 $$، می‌توان گفت $$ \left ( \frac { h } { f } \right ) \circ \gamma $$ درون دایره واحد است. این بدین معنی است که $$ 1+ \frac { h } { f } = \frac { f + h } { f } $$، منحنی $$ \gamma $$ را به درون یک دیسک واحد با مرکز $$ 1 $$ تصویر می‌کند. در نتیجه:

$$ \large \operatorname {Ind} \left ( \left ( \frac { f + h } { f} \right ) \circ \gamma , 0 \right ) = 0 $$

تابع $$ g = \frac { f + h } { f } $$ را در نظر می‌گیریم. معادله بالا می‌گوید $$ \mathrm {Ind} ( g \circ \gamma , 0 ) = 0 $$ است. بنابراین، $$ \int _ \gamma \frac {g'}{g} d z = 0 $$ (در بالا نشان دادیم که $$ g $$ صفر یا قطبی روی $$ \gamma $$ ندارد).

اکنون، به سادگی داریم: $$ \frac {g'} { g } = \frac {(f+h)'}{f + h } - \frac {f'}{f} $$. بنابراین، خواهیم داشت:

$$ \large \begin {align*} \operatorname {Ind} ( g \circ \gamma , 0 ) & = \int _ { \gamma } \frac { g ^ { \prime } } { g } d z = \int _ { \gamma } \frac { ( f + h ) ^ { \prime } } { f + h } d z - \int _ { \gamma } \frac { f ^ { \prime } } { f } d z = 0 \\ & \Rightarrow \operatorname {Ind} ( ( f + h ) \circ \gamma , 0 ) = \operatorname {Ind} ( f \circ \gamma , 0 ) \end {align*} $$

حال، طبق معادله‌های (۵) و (۶)، $$ Z _ { f , \gamma } - P _ { f , \gamma} = Z _ { f + h , \gamma } - P _ { f + h , \gamma } $$ و این یعنی ثبات قضیه روشه کامل شده است.

نتیجه: طبق فرضیات مشابه، اگر $$ h $$ و $$ f $$ تحلیلی (بدون قطب) باشند، آنگاه:

$$ \large Z _ { f , \gamma } = Z _ { f + h , \gamma } $$

اثبات: از آنجا که توابع تحلیلی هستند، هر دو مقدار $$ P _ { f , \gamma } $$ و $$ P _ { f + h , \gamma } $$ برابر با صفر خواهند بود. بنابراین، معادله (۴) نشان می‌دهد که $$ Z _ f = Z _ { f + h } $$.

$$ h $$ را به عنوان یک آشفتگی کوچک برای $$ f $$ در نظر می‌گیریم.

مثال ۴: نشان دهید همه پنج صفر $$ z ^ 5 + 3 z + 1 $$ درون منحنی $$ C _ 2 : |z| = 2 $$ هستند.

حل: فرض می‌کنیم $$ f ( z ) = z ^ 5 $$ و $$ h ( z ) = 3 z + 1 $$. واضح است که هر پنج ریشه $$ f $$ (در واقع یک ریشه با ۵ بار تکرار) درون $$ C _ 2 $$ قرار دارند. همچنین، واضح است که روی $$ f $$ نامساوی $$ | h | < 7 < 32 = |f| $$ را داریم. نتیجه قضیه روشه بیان می‌کند که هر ۵ ریشه $$ f + h = z ^ 5 + 3 z + 1 $$ باید درون منحنی باشند.

مثال ۵: نشان دهید $$ z + 3 + 2 e ^ z $$ یک ریشه در سمت چپ صفحه مختلط دارد.

حل: فرض کنید $$ f ( z ) = z + 3 $$ و $$ h ( z ) = 2 e ^ z $$. کانتور از $$ - i R $$ تا $$ i R $$ را در طول محور $$ y $$ و سپس نیم‌دایره سمت چپ به شعاع $$ R $$ را که از $$ - i R $$ بر می‌گردد در نظر بگیرید. کانتور $$ C _ 1 + C _ R $$ در شکل زیر نشان داده شده است.

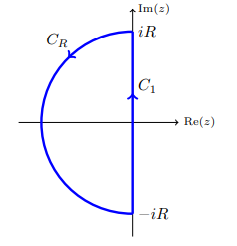
برای به کار بردن نتیجه قضیه روشه باید (برای $$ R $$ بزرگ) نامساوی $$ | h | < | f | $$ را روی $$ C _ 1 + C _ R $$ بررسی کنیم. روی $$ C _ 1 $$، داریم:‌ $$ z = i y $$. در نتیجه:

$$ \large | f ( z ) | = | 3 + i y | \geq 3 , \quad | h ( z ) | = 2 \left | \mathrm { e } ^ { i y } \right | = 2 $$

بنابراین، روی $$ C _ 1 $$، داریم: $$ | h | < | f | $$.

روی $$ C _ R $$، داریم: $$ z = x + i y $$ که $$ x < 0 $$ و $$ | z | = R $$ است. در نتیجه، برای $$ R $$ بزرگ، $$ | f ( z ) | > R - 3 $$ است و از آنجا که $$ x < 0 $$ است، $$ | h ( z ) | = 2 | e ^ { x + i y } | = 2 e ^ x < 2 $$. بنابراین، روی $$ C _ R $$، داریم: $$ | h | < | f | $$.

تنها صفر $$ f $$ در $$ z = - 3 $$ است که درون کانتور قرار دارد. بنابراین، طبق نتیجه‌گیری قضیه روشه، $$ f + h $$ تعداد مشابهی ریشه با $$ f $$ درون کانتور دارد که این تعداد ۱ است. اگر $$ R $$ به بینهاست میل کند، می‌بینیم که $$ f + g $$ تنها یک ریشه در کل نیم‌صفحه دارد.

اثبات قضیه اساسی جبر

قضیه روشه را می‌توان برای اثبات قضیه اساسی جبر نیز به کار برد. بدین منظور، فرض کنید عبارتِ

$$ \large P ( z ) = z ^ n + a _ { n - 1 } z ^ { n - 1 } + \ldots + a _ 0 $$

یک چندجمله‌ای مرتبه $$ n $$ باشد. همچنین فرض کنید $$ f ( z ) = z ^ n $$ و $$ h = P - f $$. عدد $$ R $$ را به گونه‌ای انتخاب می‌کنیم که $$ R > \max ( 1 , n | a _ { n - 1 } | , \ldots , n | a _ 0 | ) $$. در نتیجه، روی $$ | z | = R$$، داریم:

$$ \large | h | \leq \left | a _ { n - 1 } \right | R ^ { n - 1 } + \left | a _ { n - 2 } \right | R ^ { n - 2 } + \ldots + \left | a _ { 0 } \right | \leq \frac { R } { n } R ^ { n - 1 } + \frac { R }{ n } R ^ { n - 2 } + \ldots + \frac { R } { n } < R ^ { n } $$

روی $$ | z | = R $$، داریم: $$ | f ( z ) | = R ^ n $$. بنابراین، نشان دادیم که روی منحنی $$ | h | < | f | $$ است. در نتیجه، طبق نتیجه قضیه روشه، $$ f + h $$ و $$ f $$ تعداد مشابهی صفر درون $$ | z | = R $$ دارند. از آنجا که می‌دانیم $$ f $$ دقیقاً $$ n $$ صفر درون منحنی دارد، برای $$ f + h $$ نیز چنین است. اکنون $$ R $$ را به بینهایت میل می‌دهیم. بنابراین، نشان دادیم که دقیقاً $$ n $$ صفر درون کل صفحه وجود دارد.

نکته: این اثبات یک محدوده برای صفرها ارائه می‌دهد که اندازه همه آن‌ها کوچک‌تر یا مساوی $$ \max ( 1 , n | a _ { n - 1 }| , \ldots , n | a _ 0 | ) $$ است.

اگر این مطلب برای شما مفید بوده است، آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

بر اساس رای ۶ نفر

آیا این مطلب برای شما مفید بود؟

اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.

ثبت نظر

منابع:

Complex Analysis with Applications

سید سراج حمیدی (+)

سید سراج حمیدی دانش‌آموخته مهندسی برق است و به ریاضیات و زبان و ادبیات فارسی علاقه دارد. او آموزش‌های مهندسی برق، ریاضیات و ادبیات مجله فرادرس را می‌نویسد.