پیشتر در وبلاگ فرادرس مفاهیم مربوط به آونگ ساده را توضیح دادیم. بنابراین در این مطلب قصد داریم تا نحوه بدست آوردن معادله دیفرانسیل حاکم بر آونگ مرکب را توضیح داده و یکی از پاسخهای آن را در حالت نوسانی خاصی بدست آوریم. البته پیشنهاد میشود قبل از مطالعه این مطلب، مطالب معادلات دیفرانسیل ، ارتعاشات چند درجه آزادی ، آونگ ساده و معادله اویلر لاگرانژ را مطالعه فرمایید.
آونگ مرکب چیست؟
آونگ مرکب و یا به تعبیری آونگ ترکیبی به سیستمی با دو درجه آزادی گفته میشود. این آونگ از دو رابط و دو جرم تشکیل شده و نوسان هریک از دو جرم روی جرم دوم تاثیرگذار است.
بدون شک نحوه حرکت آونگ مرکب یکی از رفتارهای فیزیکی جالب در طبیعت محسوب میشود که در این مطلب این رفتار را با استفاده از ابزار ریاضیات توضیح خواهیم داد.
در حالتی که آونگ ساده به میزانی اندک از حالت تعادلش منحرف شود، پاسخ معادله حرکتِ آن به صورت ترکیبی از ترمهای سینوسی و کسینوسی بدست خواهد آمد.
آونگ مرکب نسبت به آونگ ساده به کلی دارای رفتاری متفاوت است. در مواردی که دامنه نوسانات آونگ اندک باشد، سیستم پدیده ضربان یا Beat را از خودش نشان میدهد. همچنین گفتنی است که مشخصههای نوسانی یک آونگ مرکب با گذشت زمان ناپایدار میشود.
در ادامه مدلی ریاضیاتی را در مورد نوسان آونگ ارائه خواهیم داد و پاسخ آن را نیز در شرایط مختلف مورد بررسی قرار میدهیم.
معادلات لاگرانژ
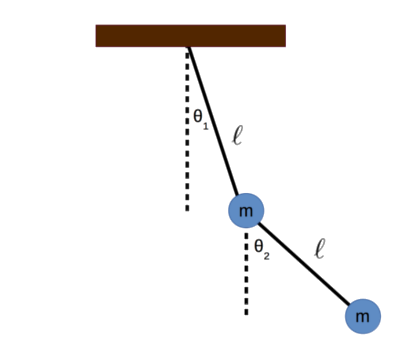
معادلات حاکم بر یک آونگ مرکب را میتوان به دو صورت بدست آورد. در روش اول قادر خواهیم بود با استفاده از قوانین نیوتن عمل کرده و معادلات حاکم بر آونگ را بدست آوریم. در روش دوم نیز میتوان با استفاده از مفهوم انرژی، معادله اویلر لاگرانژ را نوشته و شکل دیفرانسیلی معادلات را بدست آوریم. مدلی ساده شده از یک آونگ مرکب با دو جرم متفاوت در شکل زیر نشان داده شده است.
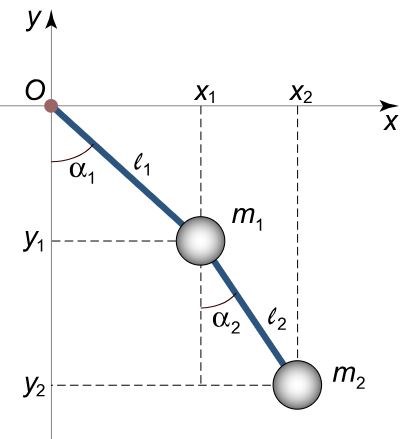
توجه داشته باشید که میلههای رابط، بدون جرم در نظر گرفته شدهاند. همچنین طول آنها نیز برابر با l 1 , l 2 \large l_1 , l _ 2 l 1 , l 2
x 1 = l 1 sin α 1 , x 2 = l 1 sin α 1 + l 2 sin α 2 , y 1 = – l 1 cos α 1 , y 2 = – l 1 cos α 1 – l 2 cos α 2 \large \begin {align*} { { x _ 1 } = { l _ 1 } \sin { \alpha _1 } , \; \; } \kern-0.3pt{{x_2} = {l_1}\sin {\alpha _1} + {l_2}\sin {\alpha _2},\;\;} \kern-0.3pt { { y _1 } = – { l _ 1 } \cos{\alpha _1},\;\;}\kern-0.3pt{{y_2} = – { l _ 1 } \cos{\alpha _1} – { l _ 2 } \cos { \alpha _ 2 } } \end {align*} x 1 = l 1 sin α 1 , x 2 = l 1 sin α 1 + l 2 sin α 2 , y 1 = – l 1 cos α 1 , y 2 = – l 1 cos α 1 – l 2 cos α 2
انرژیهای پتانسیل و جنبشی آونگ که به ترتیب با T , V \large \begin {align*} T , V \end {align*} T , V
T = m 1 v 1 2 2 + m 2 v 2 2 2 = m 1 ( x ˙ 1 2 + y ˙ 1 2 ) 2 + m 2 ( x ˙ 2 2 + y ˙ 2 2 ) 2 , V = m 1 g y 1 + m 2 g y 2 \large {{T = \frac { { { m _1 } v_1^ 2 } } {2} + \frac{{{m_2} v _ 2 ^ 2 } } { 2} } = {\frac{{{m_1}\left( {\dot x_1^2 + \dot y_1 ^ 2 } \right ) } } { 2 } } + { \frac { { { m _2 } \left ( {\dot x_2^2 + \dot y_2^2} \right)}}{2},\;\;}}\kern-0.3pt { { V = { m _ 1 } g { y _ 1 } + { m _ 2 } g { y _ 2 } }} T = 2 m 1 v 1 2 + 2 m 2 v 2 2 = 2 m 1 ( x ˙ 1 2 + y ˙ 1 2 ) + 2 m 2 ( x ˙ 2 2 + y ˙ 2 2 ) , V = m 1 g y 1 + m 2 g y 2
بنابراین لاگرانژین را میتوان به صورت زیر بدست آورد:
L = T – V = T 1 + T 2 – ( V 1 + V 2 ) = m 1 2 ( x ˙ 1 2 + y ˙ 1 2 ) + m 2 2 ( x ˙ 2 2 + y ˙ 2 2 ) − m 1 g y 1 – m 2 g y 2 \large \begin {align*} { L = T – V } & = { {T_1} + {T_2} – \left( { { V _ 1 } + {V_2}} \right) } \\ & = { \frac { { { m _ 1 } } } { 2 } \left ( {\dot x _ 1 ^ 2 + \dot y_1 ^ 2 } \right ) } + { \frac { { { m _2 } } }{ 2} \left( {\dot x_2^2 + \dot y_2^2} \right) }-{ { m _1 } g { y _ 1 } – { m _ 2 } g { y _ 2 } } \end {align*} L = T – V = T 1 + T 2 – ( V 1 + V 2 ) = 2 m 1 ( x ˙ 1 2 + y ˙ 1 2 ) + 2 m 2 ( x ˙ 2 2 + y ˙ 2 2 ) − m 1 g y 1 – m 2 g y 2
با مشتقگیری از کمیتها مولفههای سرعت افقی و عمودی به صورت زیر بدست میآیند.
y ˙ 1 = l 1 sin α 1 ⋅ α ˙ 1 , y ˙ 2 = l 1 sin α 1 ⋅ α ˙ 1 + l 2 sin α 2 ⋅ α ˙ 2 . \large \begin {align*} { { { \dot y } _ 1 } = { l _ 1 } \sin { \alpha _1 } \cdot { { \dot \alpha } _ 1 } ,\;\;}\kern-0.3pt {{{{\dot y}_2} = { l _ 1 } \sin { \alpha _1 } \cdot { { \dot \alpha }_1} }+{ {l_2}\sin{\alpha _2} \cdot {{\dot \alpha }_2}.}} \end {align*} y ˙ 1 = l 1 sin α 1 ⋅ α ˙ 1 , y ˙ 2 = l 1 sin α 1 ⋅ α ˙ 1 + l 2 sin α 2 ⋅ α ˙ 2 .
نهایتا انرژیهای جنبشی دو جرم برابر میشوند با:
T 1 = m 1 2 ( x ˙ 1 2 + y ˙ 1 2 ) = m 1 2 ( l 1 2 α ˙ 1 2 cos 2 α 1 + l 1 2 α ˙ 1 2 sin 2 α 1 ) = m 1 2 l 1 2 α ˙ 1 2 T 2 = m 2 2 ( x ˙ 2 2 + y ˙ 2 2 ) = m 2 2 [ ( l 1 α ˙ 1 cos α 1 + l 2 α ˙ 2 cos α 2 ) 2 + ( l 1 α ˙ 1 sin α 1 + l 2 α ˙ 2 sin α 2 ) 2 ] = m 2 2 [ l 1 2 α ˙ 1 2 cos 2 α 1 + l 2 2 α ˙ 2 2 cos 2 α 2 + 2 l 1 l 2 α ˙ 1 α ˙ 2 cos α 1 cos α 2 + l 1 2 α ˙ 1 2 sin 2 α 1 + l 2 2 α ˙ 2 2 sin 2 α 2 + 2 l 1 l 2 α ˙ 1 α ˙ 2 sin α 1 sin α 2 ] = m 2 2 [ l 1 2 α ˙ 1 2 + l 2 2 α ˙ 2 2 + 2 l 1 l 2 α ˙ 1 α ˙ 2 cos ( α 1 – α 2 ) ] \large \begin {align*} { T _ 1 } = \frac{{{m_1}}}{2}\left( {\dot x_1^2 + \dot y_1^2} \right) & = {{\frac{{{m_1}}}{2}\left( {l_1^2\dot \alpha _1^2{{\cos }^2}{\alpha _1} }\right.}+{\left.{ l_1^2\dot \alpha _1^2{\sin^2}{\alpha _1}} \right) }} \\ & = {\frac { { { m _ 1 } } } {2 } l_1^2\dot \alpha _1 ^ 2 } & \\\\ { T _ 2 } = \frac{{{m_2}}}{2}\left( {\dot x_2^2 + \dot y_2^2} \right) & = \frac{{{m_2}}}{2} \left [ {{{\left ( { { l_ 1 } { { \dot \alpha }_1}\cos {\alpha _1} + {l_2}{{\dot \alpha }_2} \cos {\alpha _2}} \right)}^2} } \right.+ \\ & \left.{ {{\left( {{l_1}{{\dot \alpha }_1}\sin{\alpha _1} + {l_2}{{\dot \alpha }_2}\sin{\alpha _2}} \right)}^2}} \right] \\ & = {\frac{{{m_2}}}{2}\Big[ {l_1^2\dot \alpha _1^2{{\cos }^2}{\alpha _1} } + {l_2^2\dot \alpha _2^2{{\cos }^2}{\alpha _2}} }+{ 2{l_1}{l_2}{\dot \alpha _1}{\dot \alpha _2}\cos {\alpha _1}\cos {\alpha _2} } \\ & +{ l_1^2\dot \alpha _1^2{\sin^2}{\alpha _1} } + { {l_2^2\dot \alpha _2^2{\sin^2}{\alpha _2} }+{ 2{l_1}{l_2}{{\dot \alpha }_1}{{\dot \alpha }_2} \sin { \alpha _1} \sin{\alpha _2}} \Big] } \\ & = {\frac{{{m_2}}}{2}\Big[ {l_1^2\dot \alpha _1^2 + l_2^2\dot \alpha _2^2 }+{ 2{l_1}{l_2}{{\dot \alpha }_1}{{\dot \alpha }_2}\cos \left( {{\alpha _1} – {\alpha _2}} \right)} \Big] } \end {align*} T 1 = 2 m 1 ( x ˙ 1 2 + y ˙ 1 2 ) T 2 = 2 m 2 ( x ˙ 2 2 + y ˙ 2 2 ) = 2 m 1 ( l 1 2 α ˙ 1 2 cos 2 α 1 + l 1 2 α ˙ 1 2 sin 2 α 1 ) = 2 m 1 l 1 2 α ˙ 1 2 = 2 m 2 [ ( l 1 α ˙ 1 cos α 1 + l 2 α ˙ 2 cos α 2 ) 2 + ( l 1 α ˙ 1 sin α 1 + l 2 α ˙ 2 sin α 2 ) 2 ] = 2 m 2 [ l 1 2 α ˙ 1 2 cos 2 α 1 + l 2 2 α ˙ 2 2 cos 2 α 2 + 2 l 1 l 2 α ˙ 1 α ˙ 2 cos α 1 cos α 2 + l 1 2 α ˙ 1 2 sin 2 α 1 + l 2 2 α ˙ 2 2 sin 2 α 2 + 2 l 1 l 2 α ˙ 1 α ˙ 2 sin α 1 sin α 2 ] = 2 m 2 [ l 1 2 α ˙ 1 2 + l 2 2 α ˙ 2 2 + 2 l 1 l 2 α ˙ 1 α ˙ 2 cos ( α 1 – α 2 ) ]
به همین صورت انرژیهای پتانسیل دو جرم نیز به صورت زیر بدست میآیند.
V 1 = m 1 g y 1 = – m 1 g l 1 cos α 1 \large \begin {align*} { { V _ 1 } = { m _ 1 } g {y _ 1 } } = { – { m _ 1 } g { l _1 } \cos { \alpha _1} } \end {align*} V 1 = m 1 g y 1 = – m 1 g l 1 cos α 1
V 2 = m 2 g y 2 = – m 2 g ( l 1 cos α 1 + l 2 cos α 2 ) \large \begin {align*} { { V _ 2 } = { m _ 2} g { y_ 2 } }={ – { m _ 2 } g \Big( {{l_1}\cos {\alpha _1} }+{ {l_2}\cos {\alpha _2}} \Big) } \end {align*} V 2 = m 2 g y 2 = – m 2 g ( l 1 cos α 1 + l 2 cos α 2 )
نهایتا با بدست آمدن انرژیها، لاگرانژین نیز به صورت زیر بدست میآید.
L = T – V = T 1 + T 2 – ( V 1 + V 2 ) = ( m 1 2 + m 2 2 ) l 1 2 α ˙ 1 2 + m 2 2 l 2 2 α ˙ 2 2 + m 2 l 1 l 2 α ˙ 1 α ˙ 2 cos ( α 1 – α 2 ) + ( m 1 + m 2 ) g l 1 cos α 1 + m 2 g l 2 cos α 2 . \large \begin {align*} {L = T – V }={ {T_1} + {T_2} – \left( {{V_1} + {V_2}} \right) } & = {\left( {\frac{{{m_1}}}{2} + \frac{{{m_2}}}{2}} \right)l_1^2\dot \alpha _1^2 } \\ & + {\frac{{{m_2}}}{2}l_2^2\dot \alpha _2^2 } \\ & + {{m_2}{l_1}{l_2}{\dot \alpha _1}{\dot \alpha _2}\cos \left( {{\alpha _1} – {\alpha _2}} \right) } \\ & + {\left( {{m_1} + {m_2}} \right)g{l_1}\cos {\alpha _1} } \\ & + {{m_2}g{l_2}\cos {\alpha _2}.} \end {align*} L = T – V = T 1 + T 2 – ( V 1 + V 2 ) = ( 2 m 1 + 2 m 2 ) l 1 2 α ˙ 1 2 + 2 m 2 l 2 2 α ˙ 2 2 + m 2 l 1 l 2 α ˙ 1 α ˙ 2 cos ( α 1 – α 2 ) + ( m 1 + m 2 ) g l 1 cos α 1 + m 2 g l 2 cos α 2 .
پیشتر معادله اویلر لاگرانژ را به صورت زیر معرفی کردیم.
d d t ∂ L ∂ α ˙ i – ∂ L ∂ α i = 0 , i = 1 , 2. \large \begin {align*} { \frac { d } { { d t } } \frac { { \partial L}}{{\partial {{\dot \alpha } _ i} } } – \frac { { \partial L} } { { \partial {\alpha _i}}} = 0,\;\;}\kern-0.3pt{i = 1,2.} \end {align*} d t d ∂ α ˙ i ∂ L – ∂ α i ∂ L = 0 , i = 1 , 2.
المانهای موجود در رابطه فوق برابرند با:
∂ L ∂ α ˙ 1 = ( m 1 + m 2 ) l 1 2 α ˙ 1 + m 2 l 1 l 2 α ˙ 2 cos ( α 1 – α 2 ) , \large \begin {align*} {\frac{{\partial L}}{{\partial {{\dot \alpha }_1}}} \text{ = }}\kern0pt{ \left( {{m_1} + {m_2}} \right)l_1^2{{\dot \alpha }_1} }+{ {m_2}{l_1}{l_2}{{\dot \alpha }_2}\cos \left( {{\alpha _1} – {\alpha _2}} \right),} \end {align*} ∂ α ˙ 1 ∂ L = ( m 1 + m 2 ) l 1 2 α ˙ 1 + m 2 l 1 l 2 α ˙ 2 cos ( α 1 – α 2 ) , معادله ۱
∂ L ∂ α 1 = – m 2 l 1 l 2 α ˙ 1 α ˙ 2 sin ( α 1 – α 2 ) – ( m 1 + m 2 ) g l 1 sin α 1 \large \begin {align*} {\frac{{\partial L}}{{\partial {\alpha _1}}} \text{ = }}\kern0pt{ – {m_2}{l_1}{l_2}{{\dot \alpha }_1}{{\dot \alpha }_2}\sin\left( {{\alpha _1} – {\alpha _2}} \right) } – {\left( {{m_1} + {m_2}} \right)g{l_1}\sin{\alpha _1} } \end {align*} ∂ α 1 ∂ L = – m 2 l 1 l 2 α ˙ 1 α ˙ 2 sin ( α 1 – α 2 ) – ( m 1 + m 2 ) g l 1 sin α 1 معادله ۲
∂ L ∂ α ˙ 2 = m 2 l 2 2 α ˙ 2 + m 2 l 1 l 2 α ˙ 2 cos ( α 1 – α 2 ) \large \begin {align*} {\frac{{\partial L}}{{\partial {{\dot \alpha }_2}}} \text{ = }}\kern0pt{ {m_2}l_2^2{{\dot \alpha }_2} }+{ {m_2}{l_1}{l_2}{{\dot \alpha }_2}\cos \left( {{\alpha _1} – {\alpha _2}} \right) } \end {align*} ∂ α ˙ 2 ∂ L = m 2 l 2 2 α ˙ 2 + m 2 l 1 l 2 α ˙ 2 cos ( α 1 – α 2 ) معادله ۳
∂ L ∂ α 2 = m 2 l 1 l 2 α ˙ 1 α ˙ 2 sin ( α 1 − α 2 ) − m 2 g l 2 sin α 2 \large \begin {align*} {\frac { { \partial L}}{{\partial {\alpha _2}}} \text{ = }}\kern0pt{ {m_2}{l_1}{l_2}{{\dot \alpha } _ 1 } { { \dot \alpha }_2}\sin\left( {{\alpha _1} } - { {\alpha _2}} \right) }-{ {m_2}g{l_2}\sin{\alpha _2}} \end {align*} ∂ α 2 ∂ L = m 2 l 1 l 2 α ˙ 1 α ˙ 2 sin ( α 1 − α 2 ) − m 2 g l 2 sin α 2 معادله ۴
حال با توجه به معادلات ۱و۲، معادله اول اویلر لاگرانژ را میتوان به صورت زیر بیان کرد:
d d t [ ( m 1 + m 2 ) l 1 2 α ˙ 1 + m 2 l 1 l 2 α ˙ 2 cos ( α 1 − α 2 ) ] + m 2 l 1 l 2 α ˙ 1 α ˙ 2 sin ( α 1 − α 2 ) + ( m 1 + m 2 ) g l 1 sin α 1 = 0 ⇒ ( m 1 + m 2 ) l 1 2 α ¨ 1 + m 2 l 1 l 2 α ¨ 2 cos ( α 1 − α 2 ) + m 2 l 1 l 2 α ˙ 2 2 sin ( α 1 − α 2 ) + ( m 1 + m 2 ) g l 1 sin α 1 = 0 \large \begin{aligned} &\frac{d}{d t}\left[\left(m_{1}+m_{2}\right) l_{1}^{2} \dot{\alpha}_{1}+m_{2} l_{1} l_{2} \dot{\alpha}_{2} \cos \left(\alpha_{1}-\alpha_{2}\right)\right] \\ &+m_{2} l_{1} l_{2} \dot{\alpha}_{1} \dot{\alpha}_{2} \sin \left(\alpha_{1}-\alpha_{2}\right)+\left(m_{1}+m_{2}\right) g l_{1} \sin \alpha_{1}=0 \\ &\Rightarrow\left(m_{1}+m_{2}\right) l_{1}^{2} \ddot{\alpha}_{1}+m_{2} l_{1} l_{2} \ddot{\alpha}_{2} \cos \left(\alpha_{1}-\alpha_{2}\right) \\ &+m_{2} l_{1} l_{2} \dot{\alpha}_{2}^{2} \sin \left(\alpha_{1}-\alpha_{2}\right)+\left(m_{1}+m_{2}\right) g l_{1} \sin \alpha_{1}=0 \end{aligned} d t d [ ( m 1 + m 2 ) l 1 2 α ˙ 1 + m 2 l 1 l 2 α ˙ 2 cos ( α 1 − α 2 ) ] + m 2 l 1 l 2 α ˙ 1 α ˙ 2 sin ( α 1 − α 2 ) + ( m 1 + m 2 ) g l 1 sin α 1 = 0 ⇒ ( m 1 + m 2 ) l 1 2 α ¨ 1 + m 2 l 1 l 2 α ¨ 2 cos ( α 1 − α 2 ) + m 2 l 1 l 2 α ˙ 2 2 sin ( α 1 − α 2 ) + ( m 1 + m 2 ) g l 1 sin α 1 = 0
با حذف l 1 ≠ 0 \large \begin {align*} {l_1} \ne 0 \end {align*} l 1 = 0
\begin{aligned}
به طور مشابه معادلات ۳ و ۴، معادله دوم اویلر لاگرانژ را به صورت زیر نتیجه میدهند.
d d t [ m 2 l 2 2 α ˙ 2 + m 2 l 1 l 2 α ˙ 1 cos ( α 1 − α 2 ) ] − m 2 l 1 l 2 α ˙ 1 α ˙ 2 sin ( α 1 − α 2 ) + m 2 g l 2 sin α 2 = 0 ⇒ m 2 l 2 2 α ¨ 2 + m 2 l 1 l 2 α ¨ 1 cos ( α 1 − α 2 ) − m 2 l 1 l 2 α ˙ 1 2 sin ( α 1 − α 2 ) + m 2 g l 2 sin α 2 = 0. \large \begin{aligned} &\frac{d}{d t}\left[m_{2} l_{2}^{2} \dot{\alpha}_{2}+m_{2} l_{1} l_{2} \dot{\alpha}_{1} \cos \left(\alpha_{1}-\alpha_{2}\right)\right] \\ &-m_{2} l_{1} l_{2} \dot{\alpha}_{1} \dot{\alpha}_{2} \sin \left(\alpha_{1}-\alpha_{2}\right)+m_{2} g l_{2} \sin \alpha_{2}=0 \\ &\Rightarrow m_{2} l_{2}^{2} \ddot{\alpha}_{2}+m_{2} l_{1} l_{2} \ddot{\alpha}_{1} \cos \left(\alpha_{1}-\alpha_{2}\right)-m_{2} l_{1} l_{2} \dot{\alpha}_{1}^{2} \sin \left(\alpha_{1}-\alpha_{2}\right) \\ &+m_{2} g l_{2} \sin \alpha_{2}=0 . \end{aligned} d t d [ m 2 l 2 2 α ˙ 2 + m 2 l 1 l 2 α ˙ 1 cos ( α 1 − α 2 ) ] − m 2 l 1 l 2 α ˙ 1 α ˙ 2 sin ( α 1 − α 2 ) + m 2 g l 2 sin α 2 = 0 ⇒ m 2 l 2 2 α ¨ 2 + m 2 l 1 l 2 α ¨ 1 cos ( α 1 − α 2 ) − m 2 l 1 l 2 α ˙ 1 2 sin ( α 1 − α 2 ) + m 2 g l 2 sin α 2 = 0.
با حذف m 2 l 2 ≠ 0 \large \begin {align*} { m _ 2 } { l _2 } \ne 0 \end {align*} m 2 l 2 = 0
l 2 α ¨ 2 + l 1 α ¨ 1 cos ( α 1 − α 2 ) − l 1 α ˙ 1 2 sin ( α 1 − α 2 ) + g sin α 2 = 0 \large l_{2} \ddot{\alpha}_{2}+l_{1} \ddot{\alpha}_{1} \cos \left(\alpha_{1}-\alpha_{2}\right)-l_{1} \dot{\alpha}_{1}^{2} \sin \left(\alpha_{1}-\alpha_{2}\right)+g \sin \alpha_{2}=0 l 2 α ¨ 2 + l 1 α ¨ 1 cos ( α 1 − α 2 ) − l 1 α ˙ 1 2 sin ( α 1 − α 2 ) + g sin α 2 = 0
بنابراین دستگاه معادلات دیفرانسیلی که توصیف کننده سیستم است، به صورت زیر بدست میآید.
( m 1 + m 2 ) l 1 α ¨ 1 + m 2 l 2 α ¨ 2 cos ( α 1 − α 2 ) + m 2 l 2 α ˙ 2 2 sin ( α 1 − α 2 ) + ( m 1 + m 2 ) g sin α 1 = 0 l 2 α ¨ 2 + l 1 α ¨ 1 cos ( α 1 − α 2 ) − l 1 α ˙ 1 2 sin ( α 1 − α 2 ) + g sin α 2 = 0 \large \begin{aligned} &\left(m_{1}+m_{2}\right) l_{1} \ddot{\alpha}_{1}+m_{2} l_{2} \ddot{\alpha}_{2} \cos \left(\alpha_{1}-\alpha_{2}\right) \\ &+m_{2} l_{2} \dot{\alpha}_{2}^{2} \sin \left(\alpha_{1}-\alpha_{2}\right)+\left(m_{1}+m_{2}\right) g \sin \alpha_{1}=0 \\ &l_{2} \ddot{\alpha}_{2}+l_{1} \ddot{\alpha}_{1} \cos \left(\alpha_{1}-\alpha_{2}\right)-l_{1} \dot{\alpha}_{1}^{2} \sin \left(\alpha_{1}-\alpha_{2}\right)+g \sin \alpha_{2}=0 \end{aligned} ( m 1 + m 2 ) l 1 α ¨ 1 + m 2 l 2 α ¨ 2 cos ( α 1 − α 2 ) + m 2 l 2 α ˙ 2 2 sin ( α 1 − α 2 ) + ( m 1 + m 2 ) g sin α 1 = 0 l 2 α ¨ 2 + l 1 α ¨ 1 cos ( α 1 − α 2 ) − l 1 α ˙ 1 2 sin ( α 1 − α 2 ) + g sin α 2 = 0
در ادامه دستگاه معادلات بدست آمده در بالا را برای حالتی خاص حل خواهیم کرد. این حالت زمانی است که زاویههای نوسان دو جرم، اندک باشند.
نوسان اندک آونگ مرکب
فرض کنید زوایای α 1 ( t ) , α 2 ( t ) \large \begin {align*} {\alpha _1}\left( t \right) \ , \ {\alpha _2}\left( t \right) \end {align*} α 1 ( t ) , α 2 ( t )
L = T – V = ( m 1 2 + m 2 2 ) l 1 2 α ˙ 1 2 + m 2 2 l 2 2 α ˙ 2 2 + m 2 l 1 l 2 α ˙ 1 α ˙ 2 cos ( α 1 – α 2 ) + ( m 1 + m 2 ) g l 1 cos α 1 + m 2 g l 2 cos α 2 \large \begin {align*} {L = T – V } & = {\left( {\frac{{{m_1}}}{2} + \frac { {{ m _2 } } } { 2 } } \right)l_1 ^ 2 \dot \alpha _1^2 } \\ & + {\frac{{{m_2}}}{2}l_2^2\dot \alpha _2^2 } \\ & + {{m_2}{l_1}{l_2}{\dot \alpha _1}{\dot \alpha _2}\cos \left( {{\alpha _1} – {\alpha _2}} \right) } \\ & + {\left( {{m_1} + {m_2}} \right ) g{ l _ 1 } \cos {\alpha _1} } \\ & + {{m_2}g{l_2}\cos {\alpha _2} } \end {align*} L = T – V = ( 2 m 1 + 2 m 2 ) l 1 2 α ˙ 1 2 + 2 m 2 l 2 2 α ˙ 2 2 + m 2 l 1 l 2 α ˙ 1 α ˙ 2 cos ( α 1 – α 2 ) + ( m 1 + m 2 ) g l 1 cos α 1 + m 2 g l 2 cos α 2 معادله ۵
با استفاده از بسط مک لورن، نسبتهای مثلثاتی را میتوان به صورت زیر بازنویسی کرد.
cos α 1 ≈ 1 – α 1 2 2 , cos α 2 ≈ 1 – α 2 2 2 , cos ( α 1 – α 2 ) ≈ 1 – ( α 1 – α 2 ) 2 2 ≈ 1 \large \begin {align*} {\cos {\alpha _1} \approx 1 – \frac{{\alpha _1^2}}{2},\;\;}\kern-0.3pt {\cos {\alpha _2} \approx 1 – \frac{{\alpha _2 ^ 2 } } { 2 } ,\;\;} \\ \kern-0.3pt {{\cos \left( {{\alpha _1} – {\alpha _2}} \right) }\approx{ 1 – \frac{{{{\left( {{\alpha _1} – {\alpha _2}} \right ) }^ 2 } }} { 2 } }\approx{ 1 }} \end {align*} cos α 1 ≈ 1– 2 α 1 2 , cos α 2 ≈ 1– 2 α 2 2 , cos ( α 1 – α 2 ) ≈ 1– 2 ( α 1 – α 2 ) 2 ≈ 1
با استفاده از بسطهای فوق، معادله ۵ نیز به صورت زیر قابل بیان است.
L = T – V = ( m 1 2 + m 2 2 ) l 1 2 α ˙ 1 2 + m 2 2 l 2 2 α ˙ 2 2 + m 2 l 1 l 2 α ˙ 1 α ˙ 2 – ( m 1 2 + m 2 2 ) g l 1 α 1 2 + m 2 2 g l 2 α 2 2 \large \begin {align*} {L = T – V } = {\left( {\frac{{{m_1}}}{2} + \frac{{{m_2}}}{2}} \right)l_1^2\dot \alpha _1^2 }+{ \frac{{{m_2}}}{2}l_2^2\dot \alpha _2^2 } & + { { m _ 2 } { l _ 1} { l_2}{\dot \alpha _1}{\dot \alpha _2} } \\ & – {\left( {\frac{{{m_1}}}{2} + \frac{{{m_2}}}{2}} \right)g{l_1}\alpha _1^2 } \\ & + {\frac{{{m_2}}}{2}g{l_2}\alpha _2 ^ 2 } \end {align*} L = T – V = ( 2 m 1 + 2 m 2 ) l 1 2 α ˙ 1 2 + 2 m 2 l 2 2 α ˙ 2 2 + m 2 l 1 l 2 α ˙ 1 α ˙ 2 – ( 2 m 1 + 2 m 2 ) g l 1 α 1 2 + 2 m 2 g l 2 α 2 2
تا این جا لاگرانژینِ L به ازای مقادیری کوچک از α 1 , α 2 \large \begin {align*} \alpha _ 1 , \alpha _ 2 \end {align*} α 1 , α 2
d d t ∂ L ∂ α ˙ 1 – ∂ L ∂ α 1 = 0 , d d t ∂ L ∂ α ˙ 2 – ∂ L ∂ α 2 = 0. \large \begin {align*} {\frac{d}{{dt}}\frac{{\partial L}}{{\partial {{\dot \alpha }_1}}} – \frac{{\partial L}}{{\partial {\alpha _1}}} = 0 \ \ \ , \ \ \;\;}\kern-0.3pt {\frac{d}{{dt}}\frac{{\partial L}}{{\partial {{\dot \alpha }_2}}} – \frac{{\partial L}}{{\partial {\alpha _2}}} = 0.} \end {align*} d t d ∂ α ˙ 1 ∂ L – ∂ α 1 ∂ L = 0 , d t d ∂ α ˙ 2 ∂ L – ∂ α 2 ∂ L = 0.
بنابراین مشتقات جزئی، نسبت به کمیتهای α 1 , α 2 \large \begin {align*} \alpha _ 1 , \alpha _ 2 \end {align*} α 1 , α 2
∂ L ∂ α ˙ 1 = ( m 1 + m 2 ) l 1 2 α ˙ 1 + m 2 l 1 l 2 α ˙ 2 , \large \begin {align*} { \frac { { \partial L} }{ {\partial {{\dot \alpha }_1}}} = \left( {{m_1} + {m_2}} \right)l_1^2{{\dot \alpha }_1} }+{ {m_2}{l_1}{l_2}{{\dot \alpha }_2},} \end {align*} ∂ α ˙ 1 ∂ L = ( m 1 + m 2 ) l 1 2 α ˙ 1 + m 2 l 1 l 2 α ˙ 2 ,
∂ L ∂ α 1 = – ( m 1 + m 2 ) g l 1 α 1 , \large \begin {align*} \frac{{\partial L}}{{\partial {\alpha _1}}} = – \left( {{m_1} + {m_2}} \right)g{l_1}{\alpha _1}, \end {align*} ∂ α 1 ∂ L = – ( m 1 + m 2 ) g l 1 α 1 ,
∂ L ∂ α ˙ 2 = m 2 l 2 2 α ˙ 2 + m 2 l 1 l 2 α ˙ 1 , \large \begin {align*} {\frac{{\partial L}}{{\partial {{\dot \alpha }_2}}} = {m_2}l_2^2{{\dot \alpha }_2} }+{ {m_2}{l_1}{l_2}{{\dot \alpha }_1},} \end {align*} ∂ α ˙ 2 ∂ L = m 2 l 2 2 α ˙ 2 + m 2 l 1 l 2 α ˙ 1 ,
∂ L ∂ α 2 = – m 2 g l 2 α 2 \large \frac { { \partial L } } { { \partial { \alpha _ 2 } } } = – {m_2 } g { l _ 2}{\alpha _2} ∂ α 2 ∂ L = – m 2 g l 2 α 2
نهایتا دو معادله دیفرانسیل به صورت زیر بدست میآیند.
d d t [ ( m 1 + m 2 ) l 1 2 α ˙ 1 + m 2 l 1 l 2 α ˙ 2 ] + ( m 1 + m 2 ) g l 1 α 1 = 0 \large {\frac{d}{{dt}}\left[ {\left( {{m_1} + {m_2}} \right)l_1^2{{\dot \alpha }_1} }\right.}+{\left.{ {m_2}{l_1}{l_2}{{\dot \alpha }_2}} \right] }+{ \left( {{m_1} + {m_2}} \right)g{l_1}{\alpha _1} }={ 0 } d t d [ ( m 1 + m 2 ) l 1 2 α ˙ 1 + m 2 l 1 l 2 α ˙ 2 ] + ( m 1 + m 2 ) g l 1 α 1 = 0
d d t [ m 2 l 2 2 α ˙ 2 + m 2 l 1 l 2 α ˙ 1 ] + m 2 g l 2 α 2 = 0 \large {\frac{d}{{dt}}\left[ { { m _ 2}l_2^2{{\dot \alpha }_2} + {m_2}{l_1}{l_2}{{\dot \alpha }_1}} \right] }+{ {m_2}g{l_2}{\alpha _2} }={ 0 } d t d [ m 2 l 2 2 α ˙ 2 + m 2 l 1 l 2 α ˙ 1 ] + m 2 g l 2 α 2 = 0
با محاسبه مشتقات فوق دو معادله دیفرانسیل به صورت زیر حاصل میشوند.
( m 1 + m 2 ) l 1 2 α ¨ 1 + m 2 l 1 l 2 α ¨ 2 + ( m 1 + m 2 ) g l 1 α 1 = 0 \large {\left( {{m_1} + {m_2}} \right)l_1^2{{\ddot \alpha }_1} }+{ {m_2}{l_1}{l_2}{{\ddot \alpha }_2} }+{ \left( {{m_1} + {m_2}} \right)g{l_1}{\alpha _1} }={ 0 } ( m 1 + m 2 ) l 1 2 α ¨ 1 + m 2 l 1 l 2 α ¨ 2 + ( m 1 + m 2 ) g l 1 α 1 = 0
m 2 l 1 l 2 α ¨ 1 + m 2 l 2 2 α ¨ 2 + m 2 g l 2 α 2 = 0 \large {{m_2}{l_1}{l_2}{{\ddot \alpha }_1} + {m_2}l_2^2 { { \ddot \alpha }_2} }+{ {m_2}g{l_2}{\alpha _2} }={ 0 } m 2 l 1 l 2 α ¨ 1 + m 2 l 2 2 α ¨ 2 + m 2 g l 2 α 2 = 0
معادلات فوق را میتوان در قالب معادلهای ماتریسی، بیان کرد. بدین منظور در ابتدا ماتریسهای α , M , K \large \alpha , M , K α , M , K
$$ \large {\boldsymbol{\alpha} \left( t \right) = \left[ {\begin{array}{*{20}{c}}<br />
{ { \alpha _1}\left( t \right)}\\<br />
{ { \alpha _2}\left( t \right ) }<br />
\end{array}} \right],\;\;}\kern-0.3pt<br />
{M = \left[ {\begin{array}{*{20}{c}}<br />
{\left( {{m_1} + {m_2}} \right)l_1^2}&{{m_2}{l_1}{l_2}}\\<br />
{{m_2}{l_1}{l_2}}&{{m_2}l_2^2}<br />
\end{array}} \right],\;\;}\kern-0.3pt<br />
{K = \left[ {\begin{array}{*{20}{c}}<br />
{\left( {{m_1} + {m_2}} \right)g{l_1}}&0\\<br />
0&{{m_2}g{l_2}}<br />
\end{array}} \right],\;\;}\kern0pt<br />
{\mathbf{0} = \left[ {\begin{array}{*{20}{c}}<br />
0 \\<br />
0<br />
\end {array}} \right] }$$
با استفاده از ماتریسهای تعریف شده در بالا، سیستم معادلات به صورت زیر در میآیند.
M α ¨ + K α = 0 \large M\boldsymbol{\ddot \alpha} + K\boldsymbol{\alpha} = \mathbf{0} M α ¨ + K α = 0
در مطلب ارتعاشات بیان شد که معادلهای به صورت فوق، توصیف کننده ارتعاش یک جسم است؛ اما در این جا پاسخ دستگاه فوق، دو فرکانس مشخصه را به ما میدهد که به آن مودهای نرمال گفته میشود.
مودهای نرمال، بخش حقیقی توابع برداری زیر هستند.
$$ \large {\boldsymbol{\alpha} \left( t \right) = \left[ {\begin{array}{*{20}{c}}<br />
{{\alpha _1}\left( t \right)}\\<br />
{{\alpha _2}\left( t \right)}<br />
\end{array}} \right] }<br />
= {\text{Re}\left( {\left[ {\begin{array}{*{20}{c}}<br />
{{\mathbf{H}_1}}\\<br />
{{\mathbf{H}_2}}<br />
\end{array}} \right]{e^{i\omega t}}} \right) } $$
در عبارت فوق H 1 \large {\mathbf { H }_1} H 1 H 2 \large {\mathbf { H }_2} H 2 بردارهای ویژه و ω \large \omega ω ω 1 , 2 \large \omega _ { 1 , 2 } ω 1 , 2
det ( K – ω 2 M ) = 0 \large \det \left( {K – { \omega ^ 2 } M } \right ) = 0 det ( K – ω 2 M ) = 0
در مورد آونگ مرکب با قرار دادن ماتریسها در رابطه فوق، معادله به صورت زیر بدست میآید.
( m 1 + m 2 ) g 2 − ω 2 ( m 1 + m 2 ) ( l 1 + l 2 ) g + ω 4 m 1 l 1 l 2 = 0 \large { \left ( { { m _1 } + { m _ 2 } } \right) { g ^ 2 } } - { {\omega ^2}\left( {{m_1} + {m_2}} \right)\left( {{l_1} + { l _ 2 } } \right ) g }+{ { \omega ^4}{m_1}{l_1}{l_2} = 0 } ( m 1 + m 2 ) g 2 − ω 2 ( m 1 + m 2 ) ( l 1 + l 2 ) g + ω 4 m 1 l 1 l 2 = 0
همانطور که در بالا نیز مشاهده میشود، معادله بدست آمده از درجه ۴ بوده و یافتن پاسخ آن در حالت کلی مشکل خواهد بود. بدین منظور حالتی را در نظر میگیریم که طول دو رابط با هم برابر باشد (l 1 = l 2 = l \large { l _1 } = { l _ 2 } = l l 1 = l 2 = l
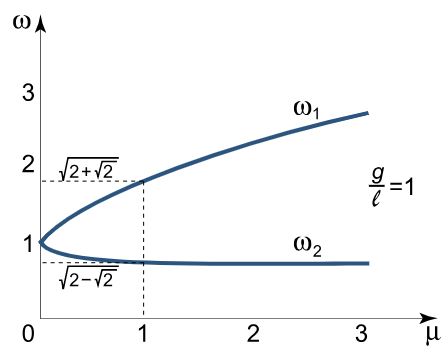
ω 1 , 2 2 = = g l [ 1 + μ ± ( 1 + μ ) μ ] , where μ = m 2 m 1 \large { \omega _{1,2} ^ 2 \text{ = }}\kern0pt = {\frac{g}{l}\left[ {1 + \mu \pm \sqrt {\left( {1 + \mu } \right)\mu } } \right],\;\;}\kern-0.3pt{\text{where}\;\;\mu = \frac{{{m_2}}}{{{m_1}}} } ω 1 , 2 2 = = l g [ 1 + μ ± ( 1 + μ ) μ ] , where μ = m 1 m 2
نمودار زیر مقادیر فرکانسهای نرمال را بر حسب مقادیر مختلف μ = m 2 m 1 \large \mu = \frac { m _ 2 } { m _ 1 } μ = m 1 m 2
همانطور که از نمودار فوق نیز بر میآید، مقادیر فرکانس تنها به نسبت جرمها وابسته است. برای حالتی که دو جرم برابر باشند، فرکانسها برابرند با:
ω 1 , 2 = g l 2 ± 2 \large { \omega _ { 1 ,2 } } = \sqrt {\frac{g}{l}} \sqrt {2 \pm \sqrt 2 } ω 1 , 2 = l g 2 ± 2
با معلوم شدن مقادیر فرکانسهای ویژه در مرحله بعدی باید بردارهای ویژه H 1 , H 2 \large H _ 1 , H _ 2 H 1 , H 2 بردار ویژه را مطالعه فرمایید).
( K – ω 2 M ) H = 0 \large \left( { K – { \omega ^ 2 } M } \right)\mathbf{H} = \mathbf{0} ( K – ω 2 M ) H = 0
در ابتدا بردار ویژه H 1 = ( H 11 , H 21 ) T \large { \mathbf{ H } _ 1 } = { \left ( { { H _{ 11 } } , { H _ {2 1 } } } \right) ^ T } H 1 = ( H 11 , H 21 ) T ترانهاده ماتریس است. در این صورت معادله فوق را میتوان برای H 1 \large H _ 1 H 1
با ضرب سطر اول در بردار ویژه، معادله زیر بدست میآید.
( 1 + μ ) ( g – ω 1 2 l ) H 11 − ω 1 2 μ l H 21 = 0 \large { \left ( { 1 + \mu } \right ) \left ( { g – \omega _ 1 ^2l} \right){H_{11}} }-{ \omega _1^2\mu l{H_{21}} = 0 } ( 1 + μ ) ( g – ω 1 2 l ) H 11 − ω 1 2 μ l H 21 = 0
بنابراین نسبت مولفههای بردار ویژه H 1 \large {\mathbf{H}_1} H 1
$$ \large \require{cancel}<br />
\Rightarrow { \frac { { { H _ {21}} }} { { {H _ {11}}}} \text{ = }}\kern0pt{ – \frac{{\left( {1 + \mu } \right)\left[ {\mu + \sqrt {\left( {1 + \mu } \right)\mu } } \right]}}{{\mu \left[ {1 + \mu + \sqrt {\left( {1 + \mu } \right)\mu } } \right]}} }<br />
= { – \sqrt {\frac{{1 + \mu }}{\mu }} } $$
با بدست آمدن نسبت مقادیر ویژه، بردار ویژه H 1 \large {\mathbf{H}_1} H 1
$$ \large {{\mathbf{H}_1} = \left[ {\begin{array}{*{20}{c}}<br />
{{H_{11}}}\\<br />
{{H_{21}}}<br />
\end{array}} \right] }={ \left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
{ – \sqrt {\frac{{1 + \mu }}{\mu }} }<br />
\end{array}} \right] } $$
با استفاده از همین روش بردار ویژه H 2 = ( H 12 , H 22 ) T \large {\mathbf{H}_2} = {\left( {{H_{12}},{H_{22}}} \right)^T} H 2 = ( H 12 , H 22 ) T
$$ \large {{\mathbf{H}_2} = \left[ {\begin{array}{*{20}{c}}<br />
{{H_{12}}}\\<br />
{{H_{22}}}<br />
\end{array}} \right] }={ \left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
{ \sqrt {\frac{{1 + \mu }}{\mu }} }<br />
\end{array}} \right] } $$
با بدست آمدن بردارهای ویژه معادله عمومی ماتریسی به صورت زیر بدست میآید.
$$ \large {\boldsymbol{\alpha} \left( t \right) = \left[ {\begin{array}{*{20}{c}}<br />
{{\alpha _1}\left( t \right)}\\<br />
{{\alpha _2}\left( t \right)}<br />
\end{array}} \right] }<br />
= {\text{Re}\left( {\left[ {\begin{array}{*{20}{c}}<br />
{{\mathbf{H}_1}}\\<br />
{{\mathbf{H}_2}}<br />
\end{array}} \right]{e^{i\omega t}}} \right) }<br />
= {{C_1}\left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
{ – \sqrt {\frac{{1 + \mu }}{\mu }} }<br />
\end{array}} \right]\cos \left( {{\omega _1}t + {\varphi _1}} \right) }<br />
+ {{C_2}\left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
{\sqrt {\frac{{1 + \mu }}{\mu }} }<br />
\end{array}} \right]\cos \left( {{\omega _2}t + {\varphi _2}} \right) } $$
در رابطه فوق C 1 , C 2 , φ 1 , φ 2 \large C _ 1 , C _ 2 , \varphi _ 1 , \varphi _ 2 C 1 , C 2 , φ 1 , φ 2
α 1 ( t = 0 ) = 0 , α 2 ( t = 0 ) = π 6 , α ˙ 1 ( t = 0 ) = 0 , α ˙ 2 ( t = 0 ) = 0 \large \alpha _ 1 (t=0) = 0 , \alpha _ 2 (t=0) = \frac {\pi}{6} , \dot {\alpha} _ 1 (t=0) = 0 , \dot {\alpha} _ 2 (t=0) = 0 α 1 ( t = 0 ) = 0 , α 2 ( t = 0 ) = 6 π , α ˙ 1 ( t = 0 ) = 0 , α ˙ 2 ( t = 0 ) = 0
با توجه به فرض فوق مقادیر φ 1 = φ 2 = 0 \large {\varphi _1} = {\varphi _2} = 0 φ 1 = φ 2 = 0 C 1 , C 2 \large C _ 1 , C _ 2 C 1 , C 2
{ α 1 ( 0 ) = C 1 + C 2 = 0 α 2 ( 0 ) = – C 1 1 + μ μ + C 2 1 + μ μ = π 6 ⇒ C 1 = – C 2 , ⇒ 2 C 2 1 + μ μ = π 6 ⇒ C 2 = π 12 μ 1 + μ ⇒ C 1 = – π 12 μ 1 + μ \large \begin {align*} {\left\{ \begin{array}{l} {\alpha _1}\left( 0 \right) = {C_1} + {C_2} = 0\\ {{\alpha _2}\left( 0 \right) = – {C_1}\sqrt {\frac{{1 + \mu }}{\mu }} }+{ {C_2}\sqrt {\frac{{1 + \mu }}{\mu }} }={ \frac{\pi }{6}} \end{array} \right. \;\;} & \Rightarrow {{C_1} = – {C_2},\;\;} \\ & \Rightarrow {2{C_2}\sqrt {\frac{{1 + \mu }}{\mu }} = \frac{\pi }{6} \;\;} \\ & \Rightarrow {{C_2} = \frac{\pi }{{12}}\sqrt {\frac{\mu }{{1 + \mu }}}\;\;} \\ & \Rightarrow {{C_1} = – \frac{\pi }{{12}}\sqrt {\frac{\mu }{{1 + \mu }}}} \end {align*} ⎩ ⎨ ⎧ α 1 ( 0 ) = C 1 + C 2 = 0 α 2 ( 0 ) = – C 1 μ 1 + μ + C 2 μ 1 + μ = 6 π ⇒ C 1 = – C 2 , ⇒ 2 C 2 μ 1 + μ = 6 π ⇒ C 2 = 12 π 1 + μ μ ⇒ C 1 = – 12 π 1 + μ μ
با بدست آمدن ثابتهای فوق، معادلات مربوط به α 1 ( t ) , α 2 ( t ) \large \begin {align*} \alpha _ 1 (t) , \alpha _ 2 (t) \end {align*} α 1 ( t ) , α 2 ( t )
α 1 ( t ) = – π 12 μ 1 + μ cos ( ω 1 t ) + π 12 μ 1 + μ cos ( ω 2 t ) α 2 ( t ) = π 12 cos ( ω 1 t ) + π 12 cos ( ω 2 t ) \large \begin{gather*} {{\alpha _1}\left( t \right) = \ } \kern0pt { – \frac{\pi }{{12}}\sqrt {\frac{\mu }{{1 + \mu }}} \cos \left( {{\omega _1}t} \right) } + {\frac{\pi }{{12}}\sqrt {\frac{\mu }{{1 + \mu }}} \cos \left( {{\omega _2}t} \right) } \\\\ {{\alpha _2}\left( t \right) \text{ = }}\kern0pt{ \frac{\pi }{{12}}\cos \left( {{\omega _1}t} \right) }+{ \frac{\pi }{{12}}\cos \left( {{\omega _2}t} \right)} \end {gather*} α 1 ( t ) = – 12 π 1 + μ μ cos ( ω 1 t ) + 12 π 1 + μ μ cos ( ω 2 t ) α 2 ( t ) = 12 π cos ( ω 1 t ) + 12 π cos ( ω 2 t )
همچنین فرکانسهای زاویهای به صورت زیر بدست میآیند.
ω 1 , 2 = g l ⋅ 1 + μ ± ( 1 + μ ) μ \large \begin{gather*} {{\omega _{1,2}} = \sqrt {\frac{g}{l}} \cdot}\kern0pt{ \sqrt {1 + \mu \pm \sqrt {\left( {1 + \mu } \right)\mu } }} \end {gather*} ω 1 , 2 = l g ⋅ 1 + μ ± ( 1 + μ ) μ
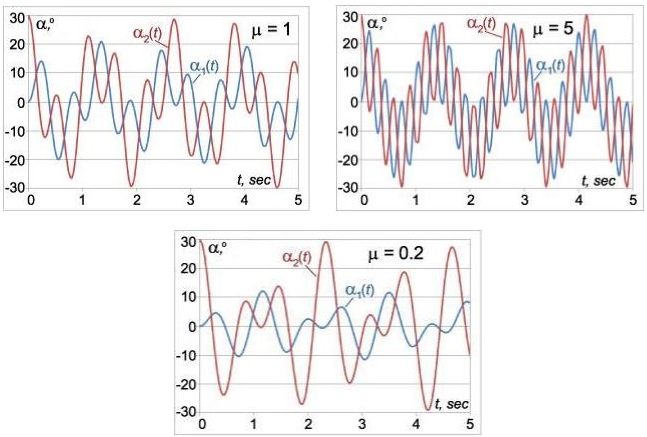
توجه داشته باشید که زوایای α \large \alpha α μ 1 = 0.2 , μ 2 = 1 , μ 3 = 5 \large \mu_1 = 0.2 , \mu _ 2 = 1 , \mu _ 3 = 5 μ 1 = 0.2 , μ 2 = 1 , μ 3 = 5 l = l 1 = l 2 = 0.25 m \large l = { l _ 1 } = { l _ 2 } = 0.25\,\text{m} l = l 1 = l 2 = 0.25 m g = 9.8 m s 2 \large g = 9.8{\large\frac{\text{m}}{{{\text{s}^2}}}\normalsize} g = 9.8 s 2 m
همانطور که از نمودارها نیز میتوان دید، دو جرم به صورت ضربانی نوسان میکنند. در حقیقت انرژی به صورت دورهای بین دو جرم منتقل میشود. زمانی که یکی از جرمها میایستد، جرم دوم با بیشترین دامنه نوسان میکند. پس از گذشت مدت زمانی مشخص، شرایط عکس شده و همین روند با گذشت زمان تکرار میشود. انیمیشن زیر نحوه نوسان دو جرم را با گذشت زمان نشان میدهد.
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز به شما پیشنهاد میشوند:
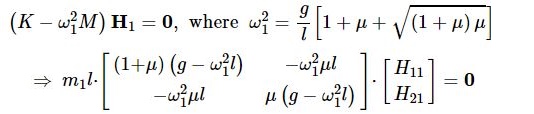













سلام
در ادامه عبارت: “حال با توجه به معادلات ۱و۲، معادله اول اویلر لاگرانژ را میتوان به صورت زیر بیان کرد:…”
اشتباها معادلات 3 و 4 جایگذاری شده اند و مجددا هم در ادامه متن تکرار شده اند.
سلام و روز شما به خیر؛
متن ویرایش و تصحیح شد.
از همراهی شما با مجله فرادرس خرسندیم.