یافتن ریشه معادله – به زبان ساده

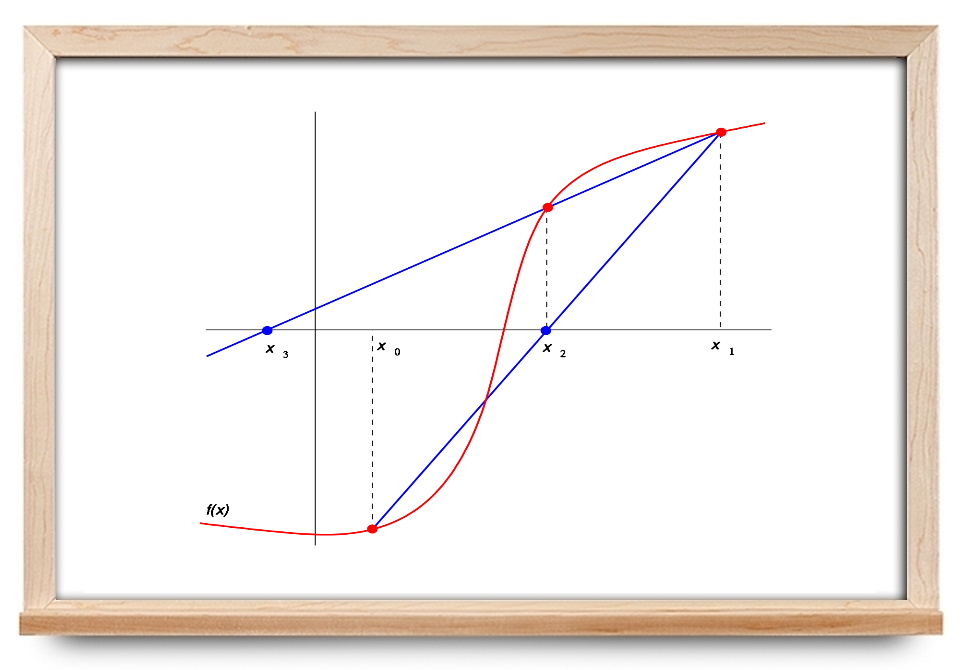
در این آموزش، با روش عددی یافتن ریشه معادله آشنا می‌شویم. می‌خواهیم معادله‌ای به فرم $$f ( x ) = 0$$ را حل کنیم. بدین منظور از روش سکانت یا وتری (Secant Method) استفاده می‌کنیم. در ادامه، روش سکانت به طور خلاصه توضیح داده شده است.

یافتن ریشه معادله

همان‌طور که گفتیم، از روش سکانت یا وتری استفاده می‌کنیم. با داشتن مقادیر اولیه $$x _ 0$$ و $$x _ 1$$، معادله خط گذرنده از نقاط $$( x _ 1 , f ( x _ 1 ))$$ و $$( x _ 2 , f ( x _ 2 ))$$ را به صورت زیر می‌نویسیم:

$$\large y = \frac { f ( x _ 2 ) - f ( x _ 1 ) } { x _ 2 - x _ 1 } ( x - x _ 2 ) + f ( x _ 2 ) .$$

ریشه این تابع خطی، مقداری از $$x$$ است که به ازای آن، $$y = 0$$ است:

$$\large x = x _ 2 - f ( x _ 2 ) \frac { x _ 2 - x _ 1 } { f ( x _ 2 ) - f ( x _ 1 ) } .$$

در ادامه، از مقدار جدید $$x$$ به عنوان $$x _ 3$$ استفاده کرده و روال را به جای $$x _ 1$$ و $$x _2$$، با $$x _ 2$$ و $$x _ 3$$ تکرار می‌کنیم. این کار را تا جایی ادامه می‌دهیم که به دقت مناسبی برسیم و اختلاف بین $$x _{n-1}$$ و $$x _ n$$ به مقدار بسیار کوچکی میل کند:

$$\large \begin {align} x _ 3 & = x _ 2 - f ( x _ 2 ) \frac { x _ 2 - x _ 1 } { f ( x _ 2 ) - f ( x _ 1 ) } , \\[6pt] x _ 4 & = x _ 3 - f ( x _ 3 ) \frac { x _ 3 - x _ 2 } { f ( x _ 3 ) - f ( x _ 2 ) } , \\[6pt] & \, \, \, \vdots \\[6pt] x _ n & = x _ { n - 1 } - f ( x _ { n - 1 } ) \frac { x _ { n - 1 } - x _ { n - 2 } } { f ( x _ { n - 1 } ) - f ( x _ { n - 2 } ) } . \end {align}$$

به طور خلاصه می‌توان گفت که روش سکانت با رابطه بازگشتی زیر تعریف می‌شود:

$$\large \begin {align*} x _ n & = x _ { n - 1 } - f ( x _ { n - 1 } ) \frac { x _ { n - 1 } - x _ { n - 2 } } { f ( x _ { n - 1 } ) - f ( x _ { n - 2 } ) } \\ & = \frac { x _ { n - 2 } f ( x _ { n - 1 } ) - x _ { n - 1 } f ( x _ { n - 2 } ) } { f ( x _ { n - 1 } ) - f ( x _ { n - 2 } ) } . \end {align*}$$

همان‌طور که از این رابطه بازگشتی می‌بینیم، روش سکانت به دو مقدار اولیه $$x _ 1$$ و $$x _ 2$$ نیاز دارد و این مقادیر باید به گونه‌ای انتخاب شوند که نزدیک ریشه باشند.

پیاده‌سازی یافتن ریشه معادله در زبان‌های برنامه‌نویسی مختلف

در ادامه،‌ برنامه یافتن ریشه معادله در زبان‌های برنامه‌نویسی مختلف ارائه شده است.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی در فرادرس

کلیک کنید

Input : equation = x3 + x - 1 
        x1 = 0, x2 = 1, E = 0.0001
Output : Root of the given equation = 0.682326
         No. of iteration=5

برنامه یافتن ریشه معادله در ++C

برنامه یافتن ریشه معادله در Java

برنامه یافتن ریشه معادله در Python

برنامه یافتن ریشه معادله در #C

برنامه یافتن ریشه معادله در PHP

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های محاسبات عددی
• آموزش محاسبات عددی با MATLAB
• مجموعه آموزش‌های دروس ریاضیات
• آموزش ریاضی پایه دانشگاهی
• روش نیوتن — به زبان ساده
• روش دو بخشی — به زبان ساده
• جذر یا محاسبه ریشه دوم عدد — به زبان ساده

^^