گرماسنجی روبشی تفاضلی (DSC) | به زبان ساده
گرماسنجی روبشی تفاضلی (DSC)، نوعی از گرماسنجی فشار ثابت به شمار میآید که برای آزمایشهای معمول در داروسازی و علم مواد کاربرد دارد. از روش گرماسنجی روبشی تفاضلی همچنین بمنظور مطالعه تغییرات شیمیایی همچون اتصال عرضی (کراسلینک) پلیمرها، ذوب و «تاشدگی پروتئینها» (Protein Folding) و گرمای جذب یا آزاده شده حین فرآیند مورد استفاده قرار میگیرد. از نام «تفاضلی» (Differential) به این دلیل استفاده میشود که گرمای ایجاد شده بر اساس یک مقدار مرجع مورد سنجش قرار میگیرد و کلمه «روبشی» (Scanning)، به تغییر دمای نمونه اشاره دارد که به طور معمول، این دما به طور خطی با زمان تغییر میکند.
مقدمه
گرماسنجی روبشی تفاضلی نوع خاصی از گرماسنجی به شمار میآید که شامل ماده نمونه و ماده مرجع باشد که هرکدام در ظروفی مجزا قرار دارند. ظرف مرجع، تنها شامل حلال (مانند آب) است درحالیکه در ظرف نمونه، مقادیر معادل از همان حلال به علاوه ماده مورد نظر برای محاسبه $$\Delta H $$ وجود دارد. $$\Delta H $$ حلال در هر دو ظرف ثابت خواهد بود بنابراین، هر اختلافی بین این دو مقدار به حضور ماده مورد سنجش مربوط میشود.
هر محفظه به طور جداگانه گرم خواهد شد و این گرم شدن به گونهای است که دما در هر دو ظرف یکسان باشد. برای این منظور از ترموکوپل بهره میگیرند. در حقیقت، دمای هر ظرف به طور پیوسته رصد میشود و اگر اختلاف دمایی مشاهده شود، برای جبران آن، ظرف با دمای کمتر، حرارت داده خواهد شد. نرخ این حرارت نسبت به دما به صورت نمودار رسم میشود.
به طور مثال، اگر هدف آزمایش، تعیین $$\Delta H $$ در فرآیند «واسرشتن» (Denaturation) پروتئین باشد، در محفظه مرجع میتوان 100 میلیلیتر آب و در محفظه نمونه میتوان علاوه بر 100 ملیلیتر آب، 1 میلیگرم هم پروتئین داشت. بنابراین، آب در تعیین $$\Delta H $$ به یک میزان در هر دو ظرف دخیل است و اختلاف موجود، تنها به حضور پروتئین مرتبط میشود.
روابط در گرماسنجی روبشی تفاضلی
در این بخش، به توصیف گرماسنجی روبشی تفاضلی و روابط آن به زبان ساده خواهیم پرداخت. رابطه زیر، تغییرات دمایی را به تغییرات آنتالپی مرتبط میکند:
$$\begin {equation} d H = \int _ { T _ {i}}^ { T _ {f}} n C_ {p} d t \end {equation}$$
- $$dH$$: نرخ تغییر آنتالپی
- $$C_P$$: ظرفیت حرارتی مولی گرماسنج (کالریمتر)
- $$dT$$: نرخ تغییر دما
- $$n$$: تعداد مول ماده
با انتگرالگیری از رابطه فوق، به رابطه زیر خواهیم رسید:
$$\begin {equation} \Delta H = n C _{p} \Delta T \end {equation}$$
ترموگرامهای تفاضلی
خروجی حاصل از روش گرماسنجی روبشی تفاضلی به صورت نموداری همچون تصویر زیر و موسوم به «ترموگرام تفاضلی» (Differential Thermogram) است. این نمودار به صورت جریان حرارتی در مقابل دما رسم میشود. آنالیز داده در این روش، به شدت به این فرض بستگی دارد که دما در نمونه و مرجع، یکسان نگاه داشته شوند.
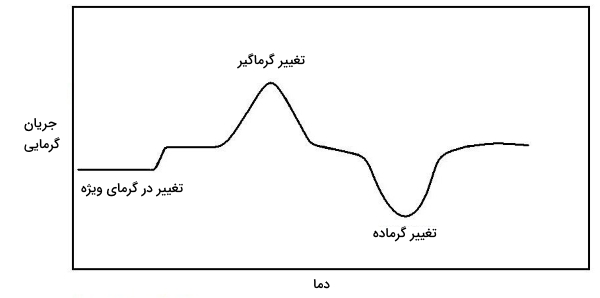
نمودار بالا تغییرات در المنت حرارتی را به هنگام افزایش دمای دو ظرف نشان میدهد. تغییر در «گرمای ویژه» (Specific Heat)، سبب تغییری کوچک در المنت حرارتی خواهد شد که بسته به نوع فرآیند، این تغییر میتواند مثبت یا منفی باشد. وجود یک واکنش گرماگیر سبب افزایش توان در المنت حرارتی خواهد شد چراکه به گرمای بیشتری برای پیشبرد واکنش و حفظ دما نیاز داریم. زمانی که یک واکنش گرماده داشته باشیم، روندی عکس روند بالا را شاهد هستیم چراکه در این خصوص، به توان کمتری از المنت برای تثبیت دما نیاز داریم. در ادامه سعی میکنیم به توصیف دقیقتری از روش گرماسنجی روبشی تفاضلی بپردازیم.
دستگاه گرماسنج روبشی تفاضلی
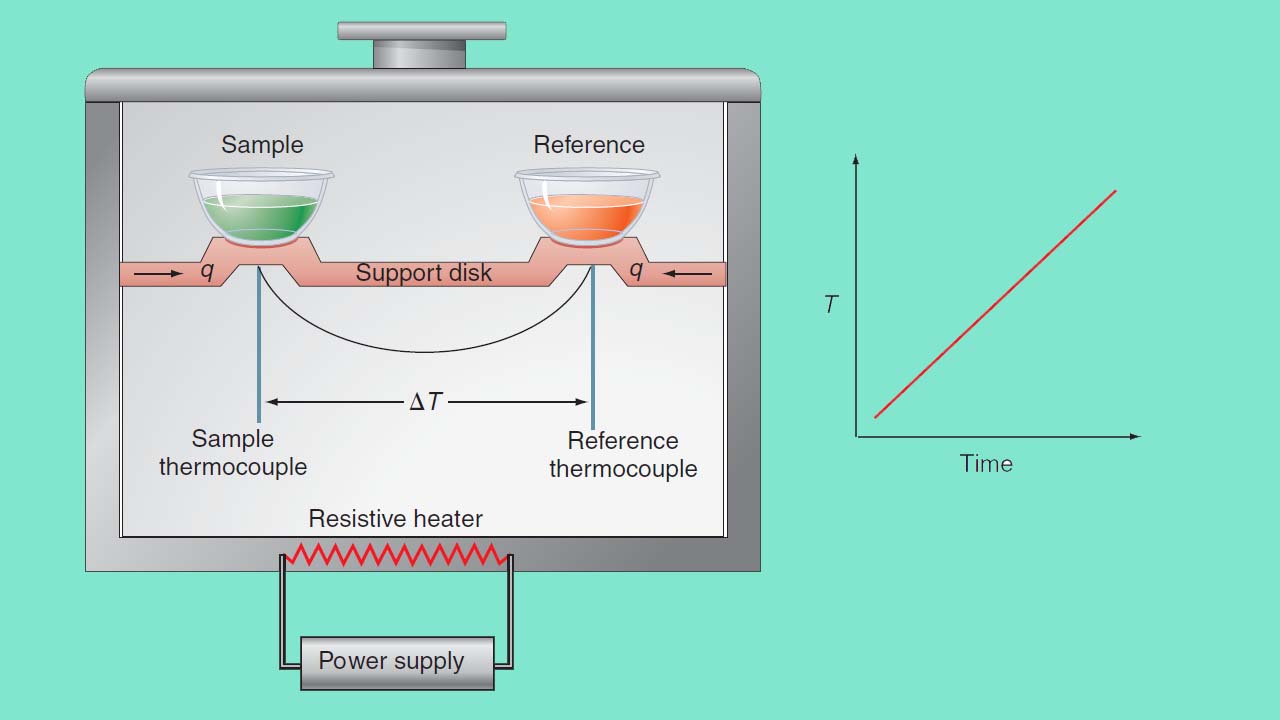
در تصویر زیر، نمایی کلی از یک دستگاه گرماسنج روبشی تفاضلی را مشاهده میکنید. این دستگاه شامل یک محفظه سنگین و عایق به همراه کلاهک است که به کمک یک گرمکن، تا دمای $$T_E$$ گرم میشود.
مواد نمونه و مرجع توسط یک پایه هادی گرما نگهداشته شدهاند. دمای نمونه و مرجع توسط یک ترموکوپل اندازهگیری میشود. در عمل و به طور معمول، مرجع شامل ظرفی خالی است.
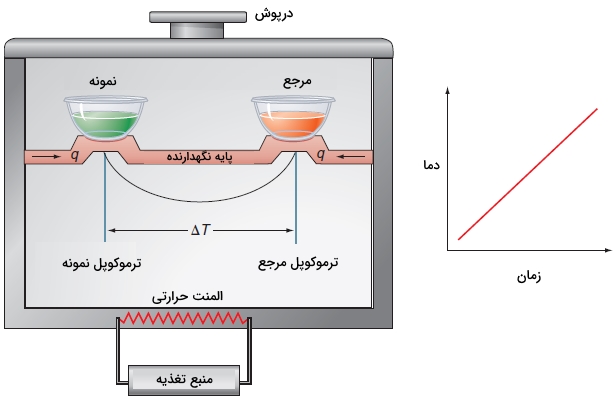
همانطور که گفته شد، دمای محفظه ($$T_E$$) به کمک یک منبع تغذیه، به صورت خطی نسبت به زمان افزایش پیدا میکند. گرما از طریق محفظه به کمک پایه هادی به نمونه میرسد. این جریان گرمایی به دلایل گرادیان ایجاد شده توسط گرمکن بوجود میآید. از آنجایی که نمونه و مرجع، هردو در یک فاصله از دیواره محفظه قرار دارند، جریان حرارت به طور یکسان به هر دو میرسد. ماده مرجع به گونهای انتخاب میشود که نقطه ذوب آن در دامنه ذوب نمونه قرار نداشته باشد. برای درک سادهتر گرماسنجی روبشی تفاضلی از یک مدل ساده تکبعدی همچون تصویر زیر برای جریان حرارت استفاده میکنیم.
جریان الکتریکی به کمک گرمکن، سبب افزایش دمای محفظه گرماسنج به دمایی بالاتر از دمای نمونه و مرجع خواهد شد که به ترتیب با نمادهای $$T_S$$ و $$T_R$$ نشان داده میشوند. جریان گرما به ازای واحد زمان را برای نمونه و مرجع به ترتیب با $$\Phi_{E S}$$ و $$\Phi_{E R}$$ نشان میدهند و واحد آنها به طور معمول با $$\mathrm{J} \mathrm{g}^{-1} s^{-1}$$ تعریف میشود.
فرض کنید فرآیندی همچون ذوب، در نمونه اتفاق بیافتد اما در مرجع، ذوبی نداشته باشیم. جریان حرارت به ازای واحد زمان دراین فرآیند را با $$\Phi(t)$$ نشان میدهیم. این عبارت، به دما وابسته است چراکه در مثال ذوب، جریان حرارت از شروع تغییر فاز تا زمان تبدیل کامل نمونه به مایع، ادامه دارد. این جریان گرمای اضافی، دمای نمونه را به میزان $$d T_{S}$$ تغییر میدهد که به دنبال آن، $$T_{E}-T_{S}$$ و $$\Phi_{E S}$$ تغییر میکنند. در طول آزمایش گرماسنجی روبشی تفاضلی مقدار $$\begin {equation} \Delta T (t) = T_ {S} (t) - T _ { R }( t ) \end {equation}$$ اندازهگیری میشود. تغییر جریان حرارت ناشی از این فرآیند را میتوان به صورت رابطه ریاضی زیر بیان کرد که در این رابطه، $$C_S$$، ظرفیت حرارتی فشار ثابت نمونه است:
$$\begin {equation} C _ { S } \frac { d T_ { S } ( t) } {d t} = \Phi _ {E S} ( t ) - \Phi ( t ) \end {equation}$$
رابطه بالا، دمای نمونه را به حرارت تولیدی ناشی از فرآیند مرتبط میکند. اگر فرآیند، گرماده باشد، $$\begin{equation}\Phi(t)<0\end{equation}$$ و اگر گرماگیر باشد، $$\begin{equation}\Phi(t)>0\end{equation}$$ خواهد بود. رابطه بالا را دوباره به گونهای مینویسیم که به طور صریح شامل تابع $$\Delta T(t)$$ باشد.
$$C _ {S} \frac {d T _{ R} (t)} {d t} +C _{S} \frac {d \Delta T ( t ) } {d t } = \Phi _ { E S } ( t ) - \Phi (t)$$
رابطه متناظر برای مرجع که در آن فقط انتقال حرارت داشته باشیم، به صورت زیر خواهد بود:
$$C _ { R } \frac {d T _ { R } ( t ) } { d t } = \Phi _ { E R } ( t )$$

هدف اصلی در روش گرماسنجی روبشی تفاضلی اندازهگیری اختلاف شار حرارتی بین نمونه و مرجع است. در نتیجه با کم کردن دو رابطه بالا از یکدیگر، به رابطه زیر خواهیم رسید:
$$\Phi _ { E S } ( t ) - \Phi _ { E R } ( t ) = \left ( C _ { S } -C _ {R } \right) \frac {d T _{ R} ( t ) } { d t }+ C _ {S} \frac { d \Delta T ( t) } {d t } + \Phi ( t )$$
مقادیر $$Phi _ { E S }$$ و $$Phi _ { E R }$$ به طور مستقیم با اختلاف دمای $$T_{E}-T_{S}$$ و $$T_{E}-T_{R}$$ و به طور معکوس با مقاومت حرارتی $$(R_{\text {thermal}})$$ بین محفظه، نمونه و مرجع مرتبط است. مقاومت حرارتی، خاصیتی ذاتی در یک گرماسنج به شمار میآید و به کمک کالیبره کردن دستگاه میتوان مقدار آنرا بدست آورد. با توجه به توضیحات داده شده خواهیم داشت:
$$\begin {equation} \Phi _ { E S } = \frac {T _ {E} - T _ { S }}{ R _{\text {thermal}}} \\
\Phi _ {E R} = \frac { T _ { E }-T _ { R } } {R _ {\text {thermal}}} \end {equation}$$
در نتیجه به رابطه زیر خواهیم رسید:
$$\begin {equation} \Phi (t) = -\frac {\Delta T ( t ) } {R _ {\text {thermal}}} - \left ( C _ { S} - C_ {R} \right) \frac {d T _ {R }( t)} {d t } - C_ {S} \frac {d \Delta T ( t)} {d t } \end {equation}$$
رابطه بالا، جریان گرمای تولیدی به ازای واحد جرم $$(\Phi(t))$$ را به کمیت اندازهگیری شده $$\Delta T(t)$$ مرتبط میکند. در بیشتر موارد، $$T_R$$ به طور خطی با زمان افزایش پیدا میکند.
$$\begin {equation} T _ { R} ( t) = T_ {0} + \alpha t \end {equation}$$
بناراین، رابطه $$(\Phi(t))$$ به صورت زیر ساده خواهد شد:
$$\begin {equation} \Phi ( t) = - \frac { \Delta T ( t ) } {R _ {\text {thermal}}} - \alpha \left ( C _ { S } - C _ {R} \right ) - C _ { S } \frac { d \Delta T ( t ) } {d t } \end {equation}$$
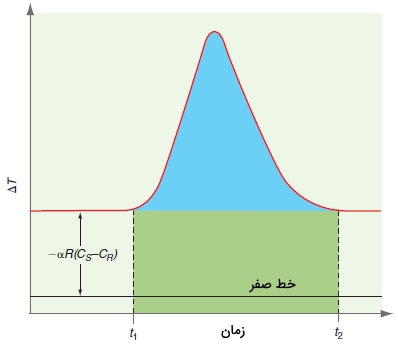
همانطور که در رابطه بالا مشاهده میکنید، $$\Delta T ( t )$$، به طور مستقیم با $$(\Phi(t))$$ مرتبط نشده است. عبارت دوم در رابطه بالا به دلیل نامساوی بودن ظرفیتهای حرارتی نمونه و مرجع ایجاد شده است. علاوه بر این، ظرفیت حرارتی نمونه با تغییر فاز، تغییر خواهد کرد. عبارت سوم در رابطه بالا با $$d \Delta T(t) / d t$$ متناسب است که شامل اثر گسترده شده $$\Delta T ( t )$$ نسبت به $$(\Phi(t))$$ و جابجا کردن آن به زمانهای طولانیتر است. نمایی از یک اسکن گرماسنجی روبشی تفاضلی را در تصویر قبل دیدیم.
با توجه به روابط مطرح شده، از آنجایی که $$\begin {equation} C _ { R } \alpha = \Phi _ {E R }( t ) \end {equation}$$ است و همچنین با توجه به تناسب $$\Delta T$$، نمودار $$C_R$$ بر حسب زمان، شکلی همانند تصویر بالا خواهد داشت. رابطه مشابهی را نیز میتوان برای «نمونه» (Sample) نوشت. در نتیجه خواهیم داشت:
$$\begin {equation} \Phi _ {E S} - \Phi _ {E R} = \alpha \left ( C _ { S } - C _ {R} \right) \end {equation}$$
هدف آزمایش گرماسنجی روبشی تفاضلی، تعیین میزان گرمای جذب یا آزاد شده در طول فرآیند به ازای واحد جرم است و از رابطه زیر بدست میآید:
$$\begin {equation} \begin {aligned}
q _ {P} & = \Delta H = \int _ {t _{1}} ^ { t_ {2}} \Phi (t) d t \\
&=- \frac{1} {R _{\text {thermal}}} \int_ {t _{1}} ^ {t _ {2}} \Delta T (t) d t - \frac {1} {R _{ \text {thermal }}} \int _ { t _ { 1}} ^ {t _ {2} } \left (-\alpha \left (C _ { S} - C_ {R} \right) \right ) d t
\end {aligned} \end {equation}$$
تفسیر نمودارهای گرماسنجی روبشی تفاضلی
تفسیر نمودارهای گرماسنجی روبشی تفاضلی باید همچون نمودارهای زیر انجام شود. در دمای ذوب، آنتالپی به شدت افزایش پیدا میکند (نمودار شماره ۱). ظرفیت حرارتی، مشتق آنتالپی نسبت به دما است که همچون نمودار ۲ در تصویر زیر دیده میشود. ظرفیت حرارتی در مایعات، بیشتر از جامدات ذکر میشود و شکل نمودار آن، همچون نمودار شماره 4 در تصویر زیر خواهد بود و دو دلیل برای بوجود آمدن این نمودار ذکر میشود. گرما به هنگام گذر از حالت ذوب، توسط نمونه جذب میشود اما دمای آن تغییر نمیکند.
با این وجود، دمای ظرف (بوته) نمونه به هنگام انتقال گرما به نمونه، افزایش پیدا میکند. بنابراین، ظرفیت حرارتی ظاهری، اگر هیچ مقاومتی در برابر جریان گرما در گرماسنج وجود نداشته باشد، نموداری شبیه به نمودار شماره ۳ خواهد داشت اما مقاومت حرارتی، موجب گسترده شدن نمودار شماره ۳ و جابجایی آن به دمای بالاتر در نمودار ۴ خواهد شد.
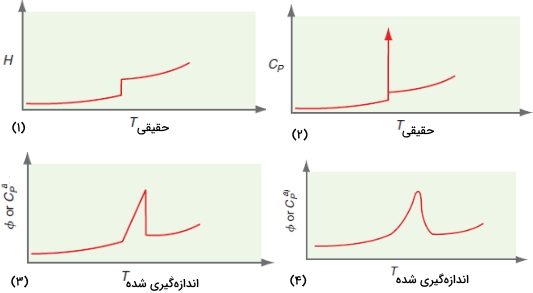
به طور مشخص، وابستگی دمایی ظرفیت حرارتی ظاهری حاصل از اسکن DSC متفاوت از وابستگی دمایی ظرفیت حرارتی حقیقی است. برای بدست آوردن ظرفیت حرارتی به طور دقیق باید از روشهای «دکانولوشن» (Deconvolution) بهره گرفت. از آنجایی که گرمای جذب یا آزاد شده در طول فرآیند به ازای واحد جرم، متناسب با مساحت زیر نمودار اسکن DSC است، این مقدار، نسبت به ظرفیت حرارتی، کمتر دچار «اغتشاش» (Distortion) ناشی از دستگاه میشود.
گرماسنجی روبشی تفاضلی روشی مستقیم برای تعیین انرژیهای حاصل از تبدیلات کانفورماسیونی درشتمولکولهای زیستی به شمار میآید که در فهم فعالیتهای زیستی این مولکولها، اهمیت بسیاری دارد. به طور ویژه، از DSC بمنظور تعیین بازه دمایی تغییرات کانفورماسیونی پروتئینها به همراه فرآیند «واسرشتن» (Denaturation) استفاده میشود.