فرادرس
رگرسیون خطی در پایتون — کدها و برنامه‌ها (بخش دوم)
در دیگر نوشتارهای مجله فرادرس، مفهوم رگرسیون خطی و همچنین نحوه محاسبات آن را خوانده‌اید. در این نوشتار قرار است با کدهای پایتون برای رگرسیون خطی، تکنیک رگرسیون خطی را در حالت ساده و چندگانه در این زبان برنامه‌نویسی و کتابخانه‌های آن اجرا کنیم. این آموزش در دو بخش که در زیر ذکر شده‌اند، ارائه می‌شود:
- بخش اول: در این قسمت، مباحث اولیه و اساسی مربوط به رگرسیون خطی آورده شده و فرمول‌های مرتبط نیز ارائه می‌شوند.
- بخش دوم: کدها و برنامه‌هایی که برای مدل‌سازی رگرسیون خطی ساده و چندگانه در پایتون لازم است در این قسمت ارائه می‌شوند.
برای آشنایی بیشتر با مفاهیم اولیه در رگرسیون خطی، نوشتارهای رگرسیون خطی — مفهوم و محاسبات به زبان ساده، رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده را بخوانید. همچنین خواندن مطلب هم خطی در مدل رگرسیونی — به زبان ساده نیز خالی از لطف نیست.
کدهای پایتون برای رگرسیون خطی
به منظور پیاده‌سازی «رگرسیون خطی ساده» (Simple Linear Regression) و «رگرسیون چندگانه» (Multiple Regression) و بررسی فرضیات آن به یک مجموعه داده احتیاج داریم که در قسمت اول این نوشتار، به بررسی آن می‌پردازیم.
در مجموعه داده‌ای که مربوط به 1030 مشاهده از مقاوت فشاری کامل (Complete Compressive Strength) یک ترکیب از مواد اولیه مختلف است، هشت متغیر توصیفی مطابق با فهرست زیر قرار دارد.
- سیمان (Cement)، برحسب کیلوگرم در مخلوط یک متر مکعب.
- سربار کوره بلند (Blast Furnace Slag)، برحسب کیلوگرم در مخلوط یک متر مکعب.
- خاکستر (Fly Ash)، برحسب کیلوگرم در مخلوط یک متر مکعب.
- آب (Water)، برحسب کیلوگرم در مخلوط یک متر مکعب.
- پلاستیزایر (Superplasticizer)، برحسب کیلوگرم در مخلوط یک متر مکعب.
- ماسه درشت دانه (Coarse Aggregate)، برحسب کیلوگرم در مخلوط یک متر مکعب.
- ماسه ریز دانه (Fine Aggregate)، برحسب کیلوگرم در مخلوط یک متر مکعب.
- طول عمر (Age) برحسب روز که در محدوده ۱ تا ۳۶۵ قرار دارد.
این مجموعه داده‌ها را می‌توانید با نام Concrete_Data.csv از اینجا با قالب فشرده دریافت کنید. در تصویر زیر نمونه‌ای از داده‌های این فایل را در اکسل مشاهده می‌کنید.
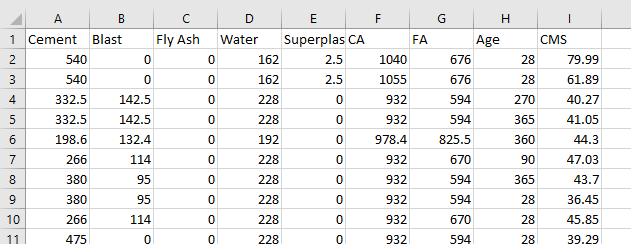
کدهای پایتون برای اجرای رگرسیون خطی
برای انجام تحلیل رگرسیونی روی مجموعه داده Concrete_Data.csv به کتابخانه‌های numpy, pandas, matplotlib احتیاج داریم. بارگذاری و فراخوانی این کتابخانه‌ها در کد زیر صورت گرفته است.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv("Concrete_Data.csv")
x = data.iloc[:,0:8]
y = data.iloc[:,8:]
فرض بر این است که فایل داده، در محل پیش‌فرض (Working Directory) پایتون قرار دارد. در غیر اینصورت باید مسیر دسترسی به این فایل را نیز در تابع pd.read_csv مشخص کنید. به این ترتیب متغیرهای توصیفی (مستقل) در متغیر x و مقادیر متغیر وابسته در y ثبت می‌شوند.
تفکیک داده‌ها به دو بخش آموزشی و آزمایشی
در این قسمت، مشاهدات را به دو گروه آموزشی (Training Set) و آزمایشی (Test Set) تقسیم می‌کنیم. این کار توسط کتابخانه sklearn صورت می‌گیرد.
from sklearn.cross_validation import train_test_split x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.2,random_state = 100)
همانطور که مشخص است ۸۰٪ از داده‌ها برای بخش آموزش و ۲۰٪ برای آزمایش در نظر گرفته شده‌اند.
رگرسیون خطی با کتابخانه sklearn
به کمک کتابخانه sklearn و کلاس LinearRegression، محاسبات مربوط به مدل رگرسیونی در متغیر lm ثبت می‌شود. نتیجه مقادیر برازش شده توسط مدل نیز برای داده‌های آموزشی محاسبه می‌شود.
from sklearn.linear_model import LinearRegression lm = LinearRegression() lm = lm.fit(x_train,y_train) #lm.fit(input,output)
خروجی با فراخوانی ـlm.coef به صورت زیر ظاهر می‌شود.
lm.coef_
array([[ 0.12415357, 0.10366839, 0.093371 , -0.13429401, 0.28804259,
0.02065756, 0.02563037, 0.11461733]])
همانطور که مشخص است، هر یک از این مقادیر به ترتیب، ضرایب متغیرهای توصیفی X1 تا X8 هستند. به منظور ثبت این متغیرها در یک چارچوب داده (DataFrame) از دستور زیر کمک می‌گیرم.
coefficients = pd.concat([pd.DataFrame(x_train.columns),pd.DataFrame(np.transpose(lm.coef_))], axis = 1)
نتیجه به صورت زیرخواهد بود.
0 Cement 0.124154 1 Blast 0.103668 2 Fly Ash 0.093371 3 Water -0.134294 4 Superplasticizer 0.288043 5 CA 0.020658 6 FA 0.025630 7 Age 0.114617
برای نمایش مقدار عرض از مبدا یا میانگین کل نیز از کد زیر استفاده می‌کنیم.
lm.intercept_ array([-34.273527])
به این ترتیب مدل رگرسیونی چندگانه مطابق با خروجی‌های ایجاد شده، شکل می‌گیرد. بر این اساس می‌توان مقادیر پیش‌بینی شده را هم نمایش داد و باقی‌مانده یا خطاها را هم محاسبه کرد.
y_pred = lm.predict(x_test) y_error = y_test - y_pred
برای محاسبه ضریب تعیین یا $$R^2$$ نیز که ابزاری برای سنجش کارایی مدل است، از دستورات زیر استفاده می‌کنیم.
from sklearn.metrics import r2_score r2_score(y_test,y_pred)
این طور به نظر می‌رسد که مقدار $$R^2$$ مناسب است و مدل به خوبی شکل گرفته است زیرا مقدار ضریب تعیین بزرگتر از ۰٫۶ است.
0.62252008774048395
رگرسیون خطی با کتابخانه statmodels
در این قسمت با استفاده از کلاس OLS، مدل رگرسیون خطی چندگانه را روی داده‌های y_train و x_train برازش می‌دهیم.
import statsmodels.api as sma X_train = sma.add_constant(x_train) ## let's add an intercept (beta_0) to our model X_test = sma.add_constant(x_test) import statsmodels.formula.api as sm lm2 = sm.OLS(y_train,X_train).fit()
نکته: متاسفانه در مدلی که توسط sm.OLS تولید می‌شود، عرض از مبدا یا مقدار میانگین کل در مدل بطور خودکار وجود ندارد و باید این گزینه را توسط sm.add_constant درخواست کنیم.
خلاصه مدل حاصل توسط دستور summary به دست می‌آید. خروجی را در ادامه می‌بینید.
lm2.summary()
"""
OLS Regression Results
==============================================================================
Dep. Variable: CMS R-squared: 0.613
Model: OLS Adj. R-squared: 0.609
Method: Least Squares F-statistic: 161.0
Date: Wed, 03 Jan 2018 Prob (F-statistic): 4.37e-162
Time: 21:29:10 Log-Likelihood: -3090.4
No. Observations: 824 AIC: 6199.
Df Residuals: 815 BIC: 6241.
Df Model: 8
Covariance Type: nonrobust
====================================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------------
const -34.2735 29.931 -1.145 0.253 -93.025 24.478
Cement 0.1242 0.010 13.054 0.000 0.105 0.143
Blast 0.1037 0.011 9.229 0.000 0.082 0.126
Fly Ash 0.0934 0.014 6.687 0.000 0.066 0.121
Water -0.1343 0.046 -2.947 0.003 -0.224 -0.045
Superplasticizer 0.2880 0.102 2.810 0.005 0.087 0.489
CA 0.0207 0.011 1.966 0.050 2.79e-05 0.041
FA 0.0256 0.012 2.131 0.033 0.002 0.049
Age 0.1146 0.006 19.064 0.000 0.103 0.126
==============================================================================
Omnibus: 3.757 Durbin-Watson: 2.033
Prob(Omnibus): 0.153 Jarque-Bera (JB): 3.762
Skew: -0.165 Prob(JB): 0.152
Kurtosis: 2.974 Cond. No. 1.07e+05
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.07e+05. This might indicate that there are
strong multicollinearity or other numerical problems.
"""
همانطور که مشاهده می‌کنید، خروجی ایجاد شده توسط دستور summary، بسیار مفصل است و مباحث مربوط به وجود هم‌خطی و نرمال بودن باقی‌مانده‌ها، توسط آزمون‌های «دوربین واتسون» (Durbin-Warson) و «جارک برا» (Jarque-Bera) صورت گرفته است که مشخص است فرض نرمال بودن با توجه به بزرگ بودن مقدار احتمال $$(Prob(JB)= 0.152)$$ رد نمی‌شود.
مشخص است که نتایج حاصل از دستور summary در اینجا با نتایج حاصل از مدلی که توسط lm از کتابخانه sklearn تولید شده، اندکی متفاوت است که ناشی از خطای محاسباتی است. زیرا مقادیر پیش‌بینی در هر دو مدل یکسان است.
در قسمتی از خروجی، یک جدول تحلیل واریانس (ANOVA) را مشاهده می‌کنید که به ضرایب و همچنین مقدار احتمال برای معنی‌داری هر یک از ضرایب مدل رگرسیونی پرداخته است. به غیر از عرض از مبدا (Constant) که دارای مقدار احتمال بزرگتر از ۵٪ است، بقیه متغیرها می‌توانند در مدل حضور داشته باشند. از طرفی بزرگ بودن مقدار F-statistic و همینطور کوچک بودن مقدار احتمال (Prob F-statistic) نشان از مناسب بودن مدل است.
در انتها نیز به منظور برآورد مقادیر متغیر وابسته از کد زیر کمک می‌گیریم.
y_pred2 = lm2.predict(X_test)
نکته: مقادیر برآورد شده در y_pred2 و y_pred برابر هستند ولی با استفاده از دو روش متفاوت بدست آمده‌اند.
ارزیابی صحت مدل رگرسیون خطی با پایتون
همانطور که در قسمت اول این نوشتار خواندید، ارزیابی مناسب بودن مدل می‌تواند توسط ضریب تعیین صورت گیرد. در این قسمت با استفاده از $$R^2$$ و $$R_{Adj.}^2$$ مدل را ارزیابی می‌کنیم.
در ادامه بدون هیچ تابعی و به کمک فرمول‌هایی که در بخش اول این نوشتارها مشاهده کرده‌اید، این شاخص‌ها را محاسبه می‌کنیم.
import numpy as np y_test = pd.to_numeric(y_test.CMS, errors='coerce') RSS = np.sum((y_pred2 - y_test)**2) y_mean = np.mean(y_test) TSS = np.sum((y_test - y_mean)**2) R2 = 1 - RSS/TSS R2 n=X_test.shape[0] p=X_test.shape[1] - 1 adj_rsquared = 1 - (1 - R2) * ((n - 1)/(n-p-1)) adj_rsquared
نتیجه اجرا برای مدل تولید شده توسط statsmodels به صورت زیر است:
$$\large R^2 = 0.6225 , \;\;\;\; R^2_{Adj.} = 0.60719$$
از آنجایی که ضریب تعیین و حتی ضریب تعیین تعدیل شده برای مدل بزرگتر از ۰٫۶ است، مدل مناسب به نظر می‌رسد.
شناسایی داده‌های دورافتاده (Outlier)
یکی از شرایط اجرای مدل رگرسیونی، نداشتن داده‌های پرت در میان مجموعه داده است. بنابراین باید داده‌ها را از جهت نداشتن چنین مشاهداتی مورد بررسی قرار دهیم. برای انجام این کار، ابتدا مقادیر استاندارد شده باقی‌مانده‌ها (Studentize Residuals) را محاسبه می‌کنیم. این کار به کمک تابع get_influence صورت می‌گیرد و نتیجه در متغیر resid_student ثبت می‌شود.
influence = lm2.get_influence() resid_student = influence.resid_studentized_external
با ترکیب مجموعه آموزشی و باقی‌مانده‌ها، جدولی به صورت زیر خواهیم داشت.
Cement Blast Fly Ash Water Superplasticizer CA FA Age \ 0 540.0 0.0 0.0 162.0 2.5 1040.0 676.0 28.0 1 540.0 0.0 0.0 162.0 2.5 1055.0 676.0 28.0 2 332.5 142.5 0.0 228.0 0.0 932.0 594.0 270.0 3 332.5 142.5 0.0 228.0 0.0 932.0 594.0 365.0 4 198.6 132.4 0.0 192.0 0.0 978.4 825.5 360.0 Studentized Residuals 0 1.559672 1 -0.917354 2 1.057443 3 0.637504 4 -1.170290
این خروجی توسط دستور زیر حاصل شده است که در آن مقادیر و بقای‌مانده‌ها را برای ۵ مشاهده اول در جدول بالا می‌بینید.
resid = pd.concat([x_train,pd.Series(resid_student,name = "Studentized Residuals")],axis = 1) resid.head()
نکته: برآورد باقی‌مانده استاندارد شده (Studentize Residuals)، برحسب واریانس برآورده شده برای متغیر وابسته و یک ضریب اصلاح است. که به صورت زیر محاسبه می‌شود:
$$\large {\displaystyle t_{i}={{\widehat {\varepsilon \,}}_{i} \over {\widehat {\sigma }}{\sqrt {1-h_{ii}\ }}}}$$
که $$h_{ii}$$ عناصر قطر اصلی ماتریس$$X(X^TX)^{-1}X^T$$ هستند. اگر مقدار باقی‌مانده استاندارد شده (Studentize Residuals) بزرگتر از ۳ یا کوچکتر از ۳- باشد، آن مشاهده را مقدار دور افتاده در نظر می‌گیریم. در نتیجه به نظر می‌رسد که مشاهده شماره 649، مقدار دورافتاده است.
Cement Blast Fly Ash Water Superplasticizer CA FA Age \
649 166.8 250.2 0.0 203.5 0.0 975.6 692.6 3.0
Studentized Residuals
649 3.161183
خروجی بالا به کمک دستور زیر بدست آمده است. توجه داشته باشید که شماره مشاهده مورد نظر در متغیر ind ذخیره شده است.
resid.loc[np.absolute(resid["Studentized Residuals"]) > 3,:] ind = resid.loc[np.absolute(resid["Studentized Residuals"]) > 3,:].index ind Int64Index([649], dtype='int64')
به منظور خارج کردن این مشاهده در مدل رگرسیونی از دستورات زیر استفاده می‌کنیم. تابع drop به این منظور در کد زیر گنجانده شده است.
y_train.drop(ind,axis = 0,inplace = True) x_train.drop(ind,axis = 0,inplace = True) #Interept column is not there X_train.drop(ind,axis = 0,inplace = True) #Intercept column is there
شناسایی هم‌خطی چندگانه و اصلاح آن
در ادامه شاخص VIF یا همان عامل یا «فاکتور تورم واریانس» (Variance Inflation Factor) را بدست می‌آوریم تا مشخص کنیم که آیا مدل دچار مشکل هم‌خطی است یا خیر. در حقیقیت می‌خواهیم بدانیم چه ترکیبی از متغیرها توصیفی با یکدیگر وابستگی خطی دارند.
from statsmodels.stats.outliers_influence import variance_inflation_factor [variance_inflation_factor(x_train.values, j) for j in range(x_train.shape[1])]
مقادیر حاصل از محاسبه VIF برای هر یک از متغیرها در ادامه دیده می‌شود.
[15.477582601956859, 3.2696650121931814, 4.1293255012993439, 82.210084751631086, 5.21853674386234, 85.866945489015535, 71.816336942930675, 1.6861600968467656]
معمولا اگر متغیری دارای VIF بزرگتر از ۵ باشد، آن را از مدل خارج می‌کنیم. بنابراین کدهای زیر به منظور شناسایی این امر و خارج کردن چنین متغیری از مدل به کار گرفته می‌شوند. در اینجا thresh، ملاک خروج متغیر از مدل است که همان مقدار ۵ را دارد.
def calculate_vif(x):
thresh = 5.0
output = pd.DataFrame()
k = x.shape[1]
vif = [variance_inflation_factor(x.values, j) for j in range(x.shape[1])]
for i in range(1,k):
print("Iteration no.")
print(i)
print(vif)
a = np.argmax(vif)
print("Max VIF is for variable no.:")
print(a)
if vif[a] <= thresh :
break
if i == 1 :
output = x.drop(x.columns[a], axis = 1)
vif = [variance_inflation_factor(output.values, j) for j in range(output.shape[1])]
elif i > 1 :
output = output.drop(output.columns[a],axis = 1)
vif = [variance_inflation_factor(output.values, j) for j in range(output.shape[1])]
return(output)
به این ترتیب متغیرهای چهارم (Water)، ششم و هفتم یعنی ماسه درشت (Coarse Aggregate) و ریز دانه (Fine Aggregate) از متغیرهای مدل خارج می‌شوند.
train_out.head()
با این کار، مجموعه داده‌ها به صورت زیر در خواهند آمد.
Cement Blast Fly Ash Superplasticizer Age 337 275.1 0.0 121.4 9.9 56 384 516.0 0.0 0.0 8.2 28 805 393.0 0.0 0.0 0.0 90 682 183.9 122.6 0.0 0.0 28 329 246.8 0.0 125.1 12.0 3
نکته: شماره‌هایی که در ستون اول این جدول مشاهده می‌کنید، شماره ردیف مشاهدات مربوط به مجموعه آموزشی هستند.
خارج کردن این متغیرها توسط کد زیر صورت گرفته است.
x_test.head() x_test.drop(["Water","CA","FA"],axis = 1,inplace = True) x_test.head()
در ادامه لیستی از مقادیر مجموعه آزمایشی با خروج متغیرهایی که باعث هم‌خطی شده بودند، دیده می‌شود.
Cement Blast Fly Ash Superplasticizer Age 173 318.8 212.5 0.0 14.3 91 134 362.6 189.0 0.0 11.6 28 822 322.0 0.0 0.0 0.0 28 264 212.0 0.0 124.8 7.8 3 479 446.0 24.0 79.0 11.6 7
حال به بررسی مدل رگرسیونی پس از خارج کردن این مقادیر می‌پردازیم.
import statsmodels.api as sma import statsmodels.formula.api as sm train_out = sma.add_constant(train_out) ## let's add an intercept (beta_0) to our model x_test.drop(["Water","CA","FA"],axis = 1,inplace = True) X_test = sma.add_constant(x_test) lm2 = sm.OLS(y_train,train_out).fit() lm2.summary()
همانطور که مشاهده می‌کنید تعداد اعضای مجموعه آموزشی از ۸۲۴ مشاهده به ۸۲۳ مشاهده رسیده زیرا یکی از اعضا که نقطه دورافتاده بود، از داده‌ها خارج شده است. همچنین درجه آزادی مدل (Df Model) که برابر با تعداد متغیرهای توصیفی است از ۸ به ۵ رسیده است که حاصل خارج کردن متغیرهایی است که مشکل هم‌خطی داشتند.
"""
OLS Regression Results
==============================================================================
Dep. Variable: CMS R-squared: 0.570
Model: OLS Adj. R-squared: 0.567
Method: Least Squares F-statistic: 216.3
Date: Wed, 10 Jan 2018 Prob (F-statistic): 6.88e-147
Time: 15:14:59 Log-Likelihood: -3128.8
No. Observations: 823 AIC: 6270.
Df Residuals: 817 BIC: 6298.
Df Model: 5
Covariance Type: nonrobust
====================================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------------
const -11.1119 1.915 -5.803 0.000 -14.871 -7.353
Cement 0.1031 0.005 20.941 0.000 0.093 0.113
Blast 0.0721 0.006 12.622 0.000 0.061 0.083
Fly Ash 0.0614 0.009 6.749 0.000 0.044 0.079
Superplasticizer 0.7519 0.077 9.739 0.000 0.600 0.903
Age 0.1021 0.006 16.582 0.000 0.090 0.114
==============================================================================
Omnibus: 0.870 Durbin-Watson: 2.090
Prob(Omnibus): 0.647 Jarque-Bera (JB): 0.945
Skew: 0.039 Prob(JB): 0.623
Kurtosis: 2.853 Cond. No. 1.59e+03
==============================================================================
همانطور که مشاهده می‌کنید، مقدار ضریب R-squared و Adj. R-squared نسبت به حالتی که همه متغیرها وجود داشتند کاهش داشته ولی این کاهش برای Adj. R-squared کمتر است. همین اختلاف زیاد بین دو شاخص در دو حالت گواهی دیگر بر وجود مشکل هم‌خطی است.
بررسی نرمال بودن باقی‌مانده‌ها
آماره‌های دوربین واستون (Durbin-Watson) با مقدار ۲٫۰۹۰ و همچنین آزمون جارک برا (Jarque-Bera) با مقدار ۰٫۹۴۵ کوچک هستند و فرض نرمال بودن باقی‌مانده‌ها را تایید می‌کنند.
نکته: برای آزمون نرمال بودن باقی‌مانده‌ها می‌توانید از آزمون «شاپیرو ویلک» (Shapiro-Wilk's test) نیز استفاده کنید. کد مربوط به اجرای این آزمون در ادامه آورده شده است.
from scipy import stats stats.shapiro(lm2.resid)
همانطور که مشاهده می‌کنید، آماره شاپیرو کوچک و مقدار احتمال آن که برابر با 0٫626988 است، بزرگتر از 0٫05 است در نتیجه فرض صفر که نرمال بودن باقی‌مانده‌ها است رد نخواهد شد.
(0.9983407258987427, 0.6269884705543518)
آزمون هم‌واریانسی (Homoscedasticity)
آزمون گلدفلد کوانت (Goldfeld-Quandt Test)، آخرین گام برای ارزیابی نتایج مدل رگرسیونی است. فرض صفر این آزمون، ثابت بودن واریانس و وجود هم‌واریانسی است. این امر به این معنی است که واریانس متغیر وابسته تحت تاثیر متغیرهای توصیفی نبوده و در نتیجه ثابت خواهد بود.
import statsmodels.stats.api as sms from statsmodels.compat import lzip name = ['F statistic', 'p-value'] test = sms.het_goldfeldquandt(lm2.resid, lm2.model.exog) lzip(name, test)
نتبجه اجرای این دستورات، نشانگر آن است که مقدار آماره F کوچک (0٫9903) و مقدار احتمال (p value=0٫539) است در نتیجه فرض هم‌واریانسی برای این مدل رد نمی‌شود. در اینجا هم باز هم صحت مدل مورد ارزیابی قرار می‌گیرد.
[('F statistic', 0.9903), ('p-value', 0.539)]
خلاصه و جمع‌بندی
رگرسیون یک تکنیک آماری است که در یادگیری ماشین و دادهکاوی به کار می‌رود. به همین علت کسانی که در علم داده مشغول فعالیت هستند، لازم است که بر این روش آماری مسلط شوند. در این نوشتار با جنبه‌های مختلف رگرسیون خطی در پایتون و نحوه پیاده‌سازی آن آشنا شدیم و از کتابخانه‌های مختلف آن برای حل مسائل رگرسیون خطی ساده و چندگانه کمک گرفتیم. در این بین نحوه ارزیابی صحت مدل نیز ارائه شده و مورد بحث قرار گرفت.
اگر مطلب بالا برای شما مفید بوده است، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش های آمار و احتمالات
- آموزش همبستگی و رگرسیون خطی در SPSS
- مجموعه آموزش‌های داده کاوی و یادگیری ماشین
- رگرسیون کمترین زاویه (LAR Regression) — به زبان ساده
- رگرسیون خطی — مفهوم و محاسبات به زبان ساده
- تحلیل واریانس (Anova) — مفاهیم و کاربردها
^^
مثل همیشه دکتر ری بد خوب بود.
در قسمت تفکیک داده ها، می بایست cross_validation با ساب ماژول model_selection جایگزین شود زیرا cross_validation منسوخ شده است!
مرسی عالی بود
بسیار عالی و مفید بود