رگرسیون خطی در پایتون — مفاهیم اساسی (بخش اول)
در دیگر نوشتارهای مجله فرادرس با مفهوم رگرسیون خطی و همچنین نحوه محاسبات آن آشنا شدهاید. ولی در مجموعه نوشتارهایی با عنوان رگرسیون خطی در پایتون ، قرار است با رگرسیون خطی ساده و چندگانه آشنا شده و شیوه انجام محاسبات مربوطه را با کدهای پایتون فرا بگیریم. مقالات یاد شده در دو بخش ارائه میشوند:
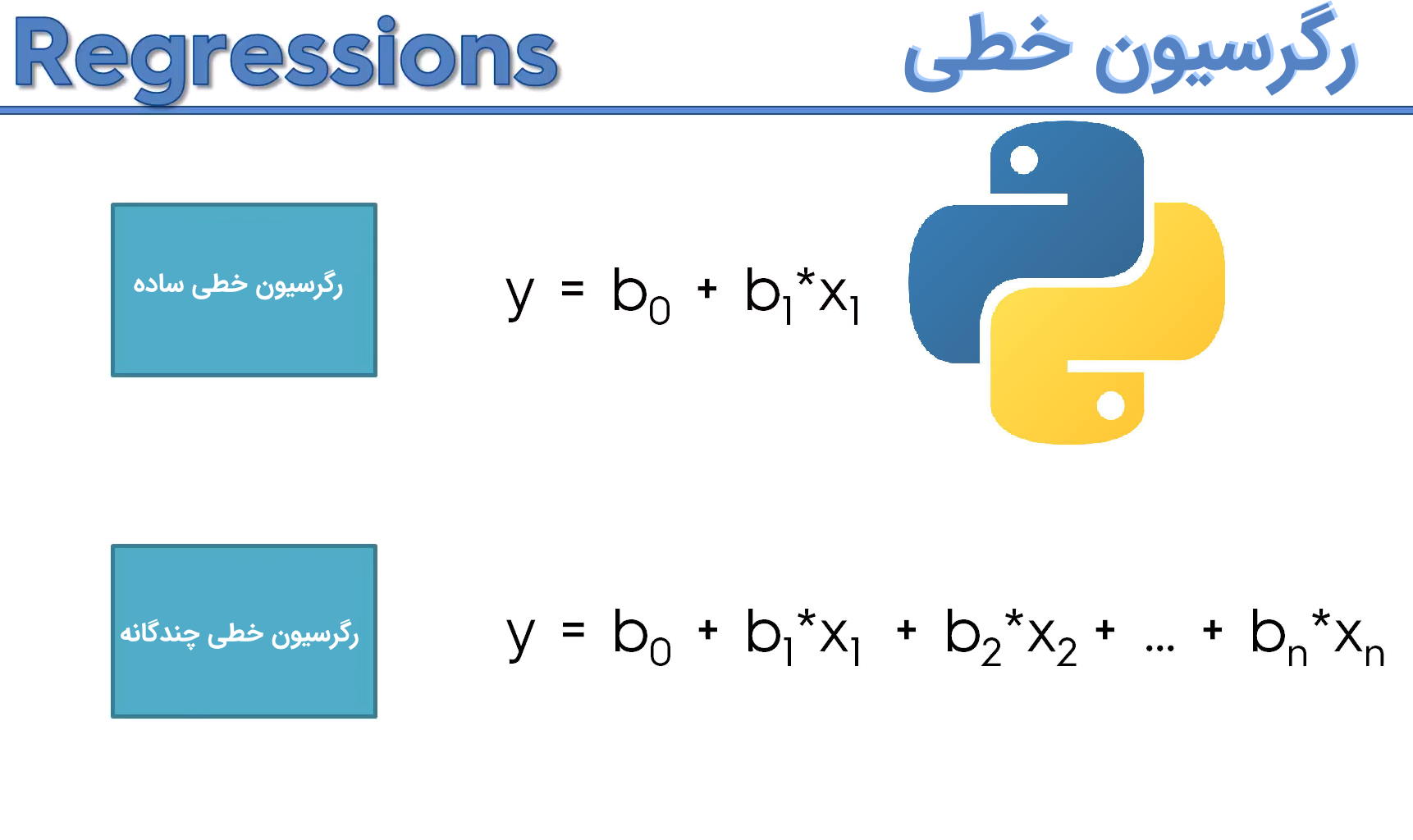
- بخش اول: در این قسمت، مباحث اولیه و اساسی مربوط به رگرسیون خطی آورده شده و فرمولهای مرتبط نیز ارائه میگردند.
- بخش دوم: کدها و برنامههایی که برای مدلسازی رگرسیون خطی ساده و چندگانه در پایتون لازم است در بخش دوم ارائه میشود.
برای آشنایی بیشتر با مفاهیم اولیه در رگرسیون خطی، نوشتارهای رگرسیون خطی — مفهوم و محاسبات به زبان ساده، رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده را بخوانید. همچنین خواندن مطلب هم خطی در مدل رگرسیونی — به زبان ساده نیز خالی از لطف نیست.
رگرسیون خطی در پایتون
«رگرسیون خطی» (Linear Regression) به عنوان یک تکنیک در یادگیری نظارت شده آماری (Statistical Supervised Machine Learning) شناخته میشود که براساس یک تابع از خطای مدل، پارامترهای آن بوسیله مشاهدات، برآورد میشود. به این ترتیب به کمک مدل پدیده آمده، میتوانیم مقدار متغیر وابسته را برحسب مقادیر متغیرهای مستقل، با تقریب مناسبی، پیشبینی کنیم.
ارتباط بین متغیر وابسته و مستقل براساس پارامترهایی است که یک مدل خطی را میسازند. در اینجا فرض بر این است که هر دو دسته متغیرهای مستقل و وابسته، از نوع کمی و عددی با مقادیر پیوسته هستند.
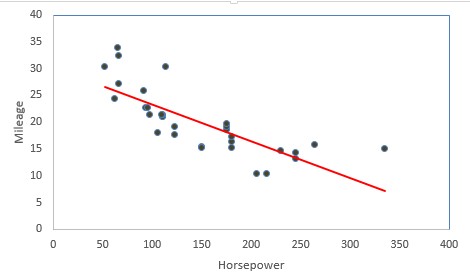
در تصویر زیر رابطه بین قدرت موتور (Horsepower) و مسافت طی شده با یک گالن سوخت (Mileage) دیده میشود. نقطههای آبی رنگ مربوط به اندازهها قدرت موتور و مسافت طی شده چندین خودرو مختلف است. محور افقی در این نمودار، قدرت موتور و محور عمودی مسافت را نشان میدهد.
همانطور که مشاهده میکنید خط قرمز رنگ میتواند به عنوان یک تابع خطی، ارتباط بین متغیر قدرت موتور به عنوان متغیر مستقل را با مسافت طی شده به عنوان متغیر وابسته نشان دهد. هر چه قدرت موتور افزایش مییابد، مصرف خودرو بیشتر شده و با یک گالن سوخت، مسافت کمتری را طی میکند. در نتیجه میتوان گفت که این رابطه، یک ارتباط معکوس بین این دو متغیر را مشخص میکند به این معنی که با افزایش یکی، دیگری کاهش مییابد.
اساس کار در رگرسیون خطی، کمینهسازی مجموع مربعات خطا است. در نتیجه معادله خطی که کمترین میزان مربعات خطا را داشته باشد، بهترین گزینه برای نمایش مدل ارتباطی بین متغیرهای مستقل و وابسته است. یادآوری میکنیم که در اینجا منظور از مدل خطی، رابطه خطی بین پارامترهای مدل است ولی ممکن است در رگرسیون خطی، متغیر وابسته با مربع متغیر مستقل دارای رابطه باشد که به این ترتیب رابطه بین این دو خطی نیست.
مثالهای زیر مسائلی هستند که توسط رابطههای رگرسیونی قابل مدلسازی هستند.
- برآورد قیمت خانه (Y) به عنوان متغیر وابسته براساس متغیرهای مستقل مساحت (X1)، تعداد اتاق خواب (X2) و نزدیکی به مراکز خرید (X3).
- برآورد مسافت طی شده برای خودروها (Y) برحسب متغیرهای مستقل اندازه محور (X1)، قدرت موتور (X2)، تعداد سیلندر (X3) و نوع سیستم دنده (X4).
- تعیین هزینههای درمان (Y) برحسب عوامل مختلف مانند سن (X1)، وزن (X2)، سابقه بیماری (X3) و ...
تفاوت بین رگرسیون خطی ساده و چندگانه
یک مدل رگرسیون خطی ساده، توسط معادله یک خط بیان میشود. همانطور که میدانید، فرم یک خط در مختصات دکارتی به صورت زیر نوشته میشود.
$$\large y=a+bx$$
که در آن $$a$$، عرض از مبدا و $$b$$ شیب خط نامیده میشود. در مدل «رگرسیون خطی ساده» (Simple Linear Regression) نیز به همین ترتیب است، به این معنی که $$a$$ میانگین کل با در نظر گرفتن مقدار صفر برای متغیر مستقل است و $$b$$ نیز ضریب متغیر مستقل نامیده میشود.
بنابراین مدل رگرسیون خطی ساده را به شکل زیر مینویسند.
$$\large Y=b_0+b_1X+\epsilon$$
و هدف در اینجا برآورد کردن پارامترهای $$b_0$$ و $$b_1$$ است. واضح است که $$b_0$$ نقش $$a$$ و $$b_1$$ نیز نقش $$b$$ را در معادله خط ایفا میکنند. از طرفی توجه داشته باشید که $$\epsilon$$ نیز میزان خطا در نظر گرفته شده که دارای توزیع نرمال با میانگین صفر و واریانس $$\sigma^2$$ است.
در «رگرسیون خطی چندگانه» (Multiple Linear Regression)، تعداد متغیرهای مستقل که گاهی آنها را «متغیرها توصیفی» (Explanatory Variables) نیز مینامند بیش از یکی است در نتیجه به جای معادله یک خط، با معادله یک صفحه در فضای $$p$$ بُعدی مواجه هستیم. به این ترتیب به دنباله معادله صفحهای هستیم که دارای کمترین مجموع مربعات خطا نسبت به صفحات دیگر باشد. همانطور که میبینید در اینجا هم اصل کمترین مربعات خطا (Principle of Least Squares) صادق است. در کل چنین، مدل رگرسیونی که برمبنای کمترین مربعات خطا بنا نهاده شده، مدل رگرسیون عادی (Ordinary Least Square) یا OLS مینامیم.
نکته: در بیشتر مدلهای رگرسیون خطی، هدف کمینهسازی مجموع مربعات خطا است. ولی گاهی به جای تابع زیان مربع (Square Loss Function) در تکنیکهای دیگر رگرسیونی از توابع زیان دیگر مانند «قدر مطلق خطا» (Absolute Difference) استفاده میکنند.
مدل رگرسیون خطی چندگانه برحسب متغیرهای توصیفی $$X_1$$ تا $$X_k$$ به صورت زیر نوشته میشود.
$$\large Y=\beta_0+\beta_1X_1+\beta_2X_2+\ldots+\beta_kX_k+\epsilon$$
فرضیات مدل رگرسیونی
فهرست زیر به معرفی فرضیههای میپردازد که در مدل رگرسیون خطی باید وجود داشته باشند. چنانچه این فرضیهها در مدل ارائه شده، وجود نداشته باشند، نمیتوان پیشبینیهای مناسبی توسط آن بدست آورد.
- باید یک رابطه خطی قوی بین متغیر وابسته و مستقل وجود داشته باشد تا مدل رگرسیون خطی، قادر به پیشبینی با خطای کم باشد.
- نمونهها در مدل رگرسیونی باید مستقل از یکدیگر باشند.
- جمله خطا در مدل رگرسیونی، دارای توزیع نرمال با میانگین صفر است.
- همخطی (Colinearity) یا همخطی چندگانه (Multicolinearity) در مدل رگرسیونی وجود نداشته باشد.
- جمله خطا، همتوزیع و مستقل باشند، بطوری که «خودهمبستگی» (Autocorrelation) بین مقادیر خطا وجود نداشته باشد.
- جمله خطا باید دارای واریانس ثابت باشد. یعنی با افزایش نمونهها یا متغیرهای توصیفی، واریانس متغیر پاسخ تغییر نکند. این ویژگی به نام «همواریانسی» (Homoscedastic) شناخته میشود. در صورتی که این ویژگی در مدل رگرسیونی وجود نداشته باشد با مشکل «ناهمواریانسی» (Heteroscedasticity) مواجه هستیم. به این ترتیب مدلی مناسب است که جمله خطای آن همواریانس باشند.
- نقاط پرت (Outlier) در مشاهدات نباید وجود داشته باشند. وجود چنین نقاطی، باعث برآورد ناصحیح و اریب پارامترهای مدل خواهد شد. در نتیجه پیشبینیها توسط مدل با دقت نامناسب رخ خواهند داد.
اندازهگیری کارایی مدل رگرسیونی
انتظار این است که تغییراتی که در متغیر وابسته وجود دارد توسط مدل رگرسیونی پیشبینی شود. سهمی که مدل رگرسیونی از تغییرات متغیر وابسته دارد را با مربع آر (R square) میشناسند.
به مربع آر، «ضریب تعیین» (Coefficient of determination) نیز میگویند. این شاخص را بوسیله رابطه زیر محاسبه میکنند.
$$\large R^2 = \dfrac{\sum y_i^2-\sum ei^2}{\sum y_i^2}=1-\dfrac{\sum e_i^2}{\sum y_i^2}$$
مقدار $$R^2$$ در بازه $$[0,1]$$ تغییر میکند. اگر برازش به درستی و کامل صورت گرفته باشد و مجموع مقدار خطا (جمله $$\epsilon$$) صفر باشد، مقدار $$R^2$$ دقیقا یک خواهد بود. به این ترتیب اگر $$R^2$$، صفر باشد بدترین حالت ممکن رخ داده و جمله خطا توانسته است همه تغییرات متغیر وابسته را در خود جای دهد در نتیجه مدل رگرسیونی هیچگونه توفیقی در برآورد صحیح مشاهدات نداشته است.
برای مثال اگر $$R^2=0.912$$ باشد به این معنی است که حدود ۹۲ درصد تغییرات متغیر $$Y$$ توسط مدل رگرسیونی قابل توصیف است. به بیان دیگر، ۹۲ درصد تغییرات متغیر وابسته توسط متغیر مستقل، بیان میشود.
البته نمیتوان کاملا به ضریب یا شاخص $$R^2$$ نیز اطمینان کرد زیرا با افزایش متغیرهای مستقل، به طور وضوح میزان شاخص $$R^2$$ افزایش مییابد در حالیکه ممکن است مدل بهتری با اضافه شدن متغیرهای جدید بوجود نیاید.
به همین دلیل معیارهای دیگری نیز برای مناسب بودن مدل رگرسیونی ایجاد شده است. برای مثال ضریب $$R^2$$ تعدیل شده (Adjusted R Square) که برحسب تعداد پارامترها، محاسبه میشود نیز به کار میآید. ضریب $$R^2$$ تعدیل شده به شکل زیر محاسبه میشود.
$$\large R_{Adj.}^2 = 1- \dfrac{e_i^2}{\sum y_i^2} \left( \dfrac{n-1}{n-k-1}\right)$$
یا به صورت معادل به شکل
$$\large R_{Adj.}^2 =1-(1-R^2)\left(\dfrac{n-1}{n-k-1}\right)$$
رابطه ۲
قابل محاسبه است. واضح است که در آن $$k$$ تعداد پارامترها، بدون در نظر گرفتن مقدار ثابت یا عرض از مبدا است.
نکته: با توجه به اصلاحی که روی $$R^2$$ صورت گرفته است، میتوان مشاهده کرد که همیشه مقدار $$R_{Adj.}^2$$ کوچکتر یا مساوی $$R^2$$ خواهد بود. تساوی زمانی رخ میدهد که $$k=0$$ باشد یعنی در مدل فقط عرض از مبدا وجود داشته باشد.
از طرفی با افزایش تعداد پارامترهای مدل، مقدار $$k$$ زیاد شده و باعث میشود که مخرج کوچکتر شود. بطور کلی ورود یک متغیر جدید باعث افزایش مقدار $$R^2$$ میشود پس با افزایش تعداد متغیرها، عبارت سمت راست رابطه ۲، بزرگ میشود. در نتیجه وقتی حاصل ضرب آنها از ۱ کم میشوند، مقدار ضریب تعدیل شده کمتر از زمانی است که این متغیر جدید به مدل اضافه نشده است.
با توجه به رابطه ۲، اگر سهم متغیر جدید در تغییر $$R^2$$ زیاد نباشد، ممکن است ضریب تعدیل شده کاهش نیز داشته باشد در نتیجه از ضریب تعدیل شده میتوان برای سنجش کارایی مدل استفاده کرد و به این ترتیب سهمی از تغییرات متغیر وابسته که توسط مدل توصیف میشود به شکل بهتری نشان داده میشود.
نکته: به عنوان یک قانون کلی میتوان در مورد ضریب $$R^2$$ تعدیل شده گفت که اگر ورود یک متغیر جدید در مدل باعث افزایش $$R^2_{Adj.}$$ شود، بهتر است آن متغیر را در مدل حفظ کرد در غیر اینصورت بهتر است آن را از مدل حذف کنیم.
بررسی صحت فرضیات مدل رگرسیونی
همانطور که اشاره کردیم، برآورد پارامترهای مدل رگرسیون، همراه با شرایطی است که پس از ایجاد مدل، باید صحت آنها بررسی شود. در ادامه این فرضیهها و نحوه بررسی صحت آنها را مرور میکنیم.
بررسی نرمال بودن خطاها
هر چند هنگامی که برآورد پارامترهای مدل رگرسیونی صورت میگیرد، هیچ صحبتی از توزیع نرمال به میان نمیآید ولی نرمال نبودن خطاها ممکن است باعث شود که کمترین مربعات خطا بواسطه عملیات محاسباتی، حاصل نشود. برای مثال هنگامی که پارامترها بدست میآیند، برای اینکه آزمون کنیم کدام یک از پارامترها (یا متغیرها) معنیدار هستند، از آزمون T استفاده میکنیم. در حالیکه اگر فرض نرمال بودن خطاها در نظر گرفته نشود، نمیتوانیم از این آزمون برای معنیداری پارامترها استفاده کنیم زیرا به نوعی آزمون T وابسته به توزیع نرمال است.
از طرفی در جدول تحلیل واریانس برای معنیداری مدل رگرسیونی از آزمون F هم استفاده میشود که بدون شرط نرمال بودن باقیماندهها، نمیتوان از آن کمک گرفت.
برای صحت بررسی نرمال بودن باقیماندهها روشهای تصویری و همچنین آزمونهای آماری مختلف وجود دارد که برای آشنایی با آنها میتوانید نوشتار آزمون نرمال بودن داده (Normality Test) — پیاده سازی در پایتون را مطالعه کنید. در اینجا به بعضی از این شیوهها اشاره خواهیم کرد.
نمودار چندک-چندک (Q-Q plot) و همچنین آزمونهایی نظیر شاپیرو ویلک، یا آزمون اندرسون دارلینگ برای انجام این امر مناسب هستند. به این ترتیب میتوانیم تشخیص دهیم که باقیماندههای حاصل از مدل رگرسیونی دارای توزیع نرمال هستند یا خیر. در صورتی که فرض نرمال بودن آنها رد شود، مدل رگرسیونی دارای اعتبار نخواهد بود و نمیتوان از آن برای پیشبینی مقادیر جدید متغیر وابسته، استفاده کرد.
از طرفی، فرض صفر بودن میانگین مقادیر خطا نیز وجود دارد که باعث میشود، توزیع نرمال برای آنها با پارامترهای صفر و $$\sigma^2$$ در نظر گرفته شود. مقادیر خطا برای هر نقطه ممکن است مقداری مثبت یا منفی باشد. میانگین صفر برای خطاها (باقیماندهها) به این معنی است که برآیند مقادیر خطا، صفر است. پس مقادیر مثبت، مقادیر منفی را خنثی میکنند و در نتیجه مجموع مقادیر خطا همیشه صفر است. در غیر اینصورت، اریبی (Biased) در برآوردها پیش میآید و مقادیر پیشبینی شده در اکثر موارد، بزرگتر یا کوچکتر از مقادیر واقعی خواهند بود.
مسئله همخطی
فرض کنید ستونهای ماتریس مقادیر متغیرهای توصیفی (X)ها، با یکدیگر همبستگی داشته باشند. در این صورت ممکن است یک ستون به صورت یک رابطه خطی با ستون دیگر نوشته شود. در این حالت ماتریس $$X'X$$ معکوسپذیر نبوده و دترمینان آن صفر است.
چنین وضعیتی مشکل همخطی (Colinearity) یا همخطی چندگانه (Multicolinearity) نامیده میشود. بطور کلی اگر رابطه کاملا خطی نیز بین متغیرهای توصیفی برقرار نباشد، باز هم وجود همبستگی بین آنها باعث افزایش واریانس برآوردگرها خواهد شد و ممکن است بعضی از متغیرها از مدل حذف شوند در حالیکه از لحاظ آماری، در آزمون فرض، معنیدار (Significant) هستند.
تشخیص همخطی، به شیوههای مختلفی صورت میگیرد که در ادامه به بعضی از آنها اشاره خواهیم کرد.
- رسم نمودار نقطهای (Scatter Plot): با رسم نمودار نقطهای، به صورت دو به دو بین متغیرهای توصیفی، وجود همبستگی یا رابطه خطی بینشان مشخص میشود. در چنین مواقعی رسم نمودار نقطهای به صورت ماتریسی صورت میگیرد تا همزمان برای همه متغیرهای توصیفی، نمودارها ظاهر شوند.
- محاسبه ضریب همبستگی (Correlation): محاسبه ماتریس ضریب همبستگی بین زوج متغیرهای توصیفی، راهنمایی برای تشخیص همخطی یا همخطی چندگانه است. اگر مقدار ضریب همبستگی بین متغیرهای توصیفی، نزدیک به 1 یا ۱- باشد، مشکل همخطی وجود دارد و برای رفع آن باید از روشهای تجزیه به مولفههای اصلی (PCA) استفاده کرد.
- محاسبه عامل تورم واریانس (Variance Inflation Factor): محاسبه این عامل، براساس مدل رگرسیونی ساخته شده، صورت میگیرد. ابتدا براساس همه متغیرها توصیفی، مدل ساخته میشود و سپس عامل تورم واریانس (VIF) برای هر متغیر محاسبه میشود. این شاخص نشان میدهد که حضور یک متغیر در مدل چقدر باعث افزایش واریانس برآوردگرها خواهد شد. هر چه این مقدار برای متغیری بیشتر باشد، همبستگی آن با متغیرها دیگر در مدل بزرگتر خواهد بود.
نکته: گاهی برای نشان دادن مشکل همخطی، از معکوس VIF نیز استفاده میکنند که به آن «اندازه تحمل» (Tolerance) میگویند. در این حالت کوچک بودن اندازه تحمل برای هر متغیر نشان از وابستگی آن با دیگر متغیرها خواهد بود.
مشکل ناهمواریانسی
به منظور شناسایی مشکل ناهمواریانسی (Heteroscedasticity)، میتوان به دو شیوه تصویری و آزمون فرض متکی بود.
- روش تصویری: پس از اجرای مدل رگرسیون و بدست آوردن مقادیر برازش شده برای متغیر وابسته ($$\hat{Y_i}$$) و همچنین مقادیر خطا ($$e_i$$)، آنها را روی یک نمودار نقطهای (Scatter) در محور مختصات دکارتی ترسیم میکنیم بطوری که مقادیر برآورد شده متغیر وابسته روی محور افقی و باقیماندهها یا خطاها روی محور عمودی باشند. اگر روند تغییرات مقادیر خطا، به صورت یک قیف افقی درآید بطوری که ابتدای قیف برای مقادیر کوچک $$Y_i$$ و قسمت بزرگتر قیف در انتها قرار داشته باشد، مسئله ناهمواریانسی وجود دارد. این امر نشان میدهد که با افزایش مقادیر $$y$$، واریانس باقیماندهها نیز در حال افزایش است.

- آزمون گلدفلد کوانت (Goldfeld-Quandt Test): در این آزمون، فرض بر این است که همواریانسی برای واریانس باقیماندهها (خطا) یا متغیر وابسته وجود دارد. در صورتی که ناهمواریانس وجود داشته باشد، همبستگی مثبت و زیادی بین متغیر وابسته و بعضی از متغیرهای توصیفی (X)ها دیده خواهد شد. همچنین نرمال بودن خطا نیز از پیشفرضهای این آزمون است. آماره آزمون گلدفلد کوانت، دارای توزیع F بوده و فرض صفر که بیانگر همواریانسی جمله خطا است رد میشود، اگر مقدار احتمال کوچکتر از $$\alpha=0.05$$ باشد. در این صورت با مشکل ناهمواریانسی مواجه هستیم.
معممولا برای رفع این مشکل، باید متغیرهای توصیفی یا مدل رگرسیونی را تغییر داد و مثلا به جای استفاده از متغیر Y، از لگاریتم یا جذر آن استفاده کرد. این تبدیل ممکن است باعث بوجود آمدن همواریانسی در مدل رگرسیونی شود.
خلاصه و جمعبندی
رگرسیون به عنوان یک تکنیک آماری، در یادگیری ماشین و دادهکاوی به کار میرود. به همین علت کسانی که در علم داده مشغول فعالیت هستند، لازم است که این روش آماری را به طور کامل فرا بگیرند. در سلسله نوشتارهای با عنوان رگرسیون خطی در پایتون با جنبههای مختلف این نوع مدل و همچنین نحوه پیادهسازی آن در پایتون آشنا شده و از کتابخانههای مختلف آن برای حل مسائل رگرسیون خطی ساده و چندگانه کمک خواهیم گرفت. در این بین نحوه ارزیابی مدل و صحت مدل ارائه شده نیز مورد بحث قرار خواهد گرفت.
در بخش اول با مفاهیم اولیه و اساسی در مورد مدلسازی رگرسیونی صحبت کردیم و همچنین فرضیاتی را که هنگام مدلسازی باید به آن پایبند باشیم، معرفی کردیم. در نوشتار بعدی به کدنویسی در پایتون و استفاده از کتابخانههای آن برای انجام محاسبات و برآورد پارامترهای مدل رگرسیونی خواهیم پرداخت و کدهای پایتون مربوط به تحلیل آنها را نیز فرا میگیریم.
برای مطالعه قسمت دوم این مطلب روی لینک زیر کلیک کنید:
اگر مطلب بالا برای شما مفید بوده است، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های آمار و احتمالات
- آموزش همبستگی و رگرسیون خطی در SPSS
- مجموعه آموزشهای داده کاوی و یادگیری ماشین
- رگرسیون کمترین زاویه (LAR Regression) — به زبان ساده
- رگرسیون خطی — مفهوم و محاسبات به زبان ساده
- تحلیل واریانس (Anova) — مفاهیم و کاربردها
^^










