پخش بار نیوتن رافسون — به زبان ساده

پخش بار، یکی از مباحث مهم در مطالعه سیستم‌های قدرت است که در آموزش‌های پیشین مجله فرادرس، مفاهیم و معادلات مربوط به آن را معرفی کردیم. همچنین با روش پخش بار گوس سایدل آشنا شدیم. الگوریتم نیوتن رافسون، متداول‌ترین الگوریتم تکراری برای حل مسئله پخش بار است. در این آموزش، پخش بار نیوتن رافسون را معرفی خواهیم کرد. پیشنهاد می‌کنیم قبل خواندن روش «پخش بار نیوتن رافسون»، آموزش «پخش بار در سیستم قدرت — مفاهیم و معادلات» را مطالعه کنید. برای آشنایی با برنامه‌نویسی پخش بار نیوتن رافسون به این لینک [+] مراجعه کنید.

قبل از آنکه درباره روش پخش بار نیوتن رافسون (Newton-Raphson Power Flow) یا NRLF بحث کنیم، ابتدا کاربرد روش نیوتن رافسون پایه را برای حل مجموعه معادلات جبری غیرخطی بیان می‌کنیم.

استخراج روش نیوتن-رافسون با استفاده از سری تیلور

یک تابع غیرخطی را که مشتق پذیر باشد، می‌توان با یک چندجمله‌ای از سری تیلور تقریب زد. تابع غیرخطی $$f (x)$$ را در نظر بگیرید. بسط تیلور این تابع حول نقطه $$x _0$$ به صورت زیر است:

$$\large f ( x ) \approx f ( x _ 0 ) + ( x - x _ 0 ) \frac { \partial f ( x _ 0 ) } { \partial x } + \frac { 1 } { 2 } ( x - x _ 0 ) ^{ 2 } \frac { \partial ^ { 2 } f ( x _ 0 ) } { \partial x ^ { 2 } } + \cdots \,\,\,\,\, (1)$$

فیلم آموزش دینامیک سیستم های قدرت 1 در فرادرس

کلیک کنید

وقتی فقط دو جمله اول بسط بالا را در نظر بگیریم، می‌گوییم $$f(x)$$ به صورت خطی تقریب زده شده است. اگر مشتق دوم را نیز نگه داریم، می‌گوییم تقریب مربعی است.

مثال ۱

تقریب خطی تابع زیر را در نقطه داده شده و با استفاده از سری تیلور تعیین کنید. تابع اصلی و تقریب خطی آن را در بازه $$-1 \leq x \leq 6$$ رسم کرده و نتایج را با هم مقایسه کنید.

$$\large f ( x ) = 4 x ^ { 2 } + 3, \,\,\,\,\, x _0 = 4$$

حل: تابع و مشتق ان در نقطه داده شده برابرند با:

$$\large \begin {align*} f ( x _ 0 ) & = 6 7 \\ \frac { \partial f ( x _ 0 ) } { \partial x } & = 8 x _ 0 = 3 2 \end {align*}$$

بنابراین، تقریب بسط تیلور خطی به صورت زیر است:

$$\large f ( x ) \approx 6 7 + ( x - 4 ) \times 3 2 \approx 3 2 x - 61$$

شکل ۱، تابع اصلی و تقریب خطی آن را نشان می‌دهد. همان‌طور که می‌بینیم، تقریب حول $$x _0$$ مناسب است؛ اما اگر از این نقطه دور شویم، فاصله تابع اصلی و تقریب خطی آن بیشتر می‌شود. نتیجه تقریب را می‌توان با جملات شامل مشتقات بالاتر بهبود داد.

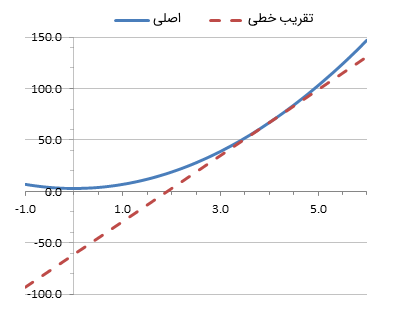
در مثال بالا، چگونگی تقریب معادله غیرخطی و محاسبه مقدار تابع در یک نقطه معین را بررسی کردیم. به طریق مشابه می‌توان از تقریب‌های خطی سری تیلور برای محاسبه جواب معادله غیرخطی و تعیین مقدار $$x$$ در معادله $$f (x )$$ استفاده کرد. در معادله (۱)، اگر از مشتق مرتبه دوم و بالاتر از آن صرف‌نظر کنیم، معادله به صورت زیر در می‌آید:

$$\large \begin {align*} f ( x ) & = f ( x _ 0 ) + ( x - x _ 0 ) \frac { \partial f ( x _ 0 ) } { \partial x } \\ f ( x ) - f ( x _ 0 ) & = ( x - x _ 0 ) \frac { \partial f ( x _ 0 ) } { \partial x } \end {align*}$$

$$\large x = x _ 0 + \left [ \frac { \partial f ( x _ 0 ) } { \partial x } \right ] ^ { - 1 } \left [ f ( x ) - f ( x _ 0 ) \right] \,\,\,\,\, (2)$$

در مثال ۱ دیدیم که نتیجه تابع تقریب خطی فقط در نزدیکی نقطه $$x _0$$ به نتیجه واقعی نزدیک است. به طریق مشابه، جواب $$x_0$$ بدون تخمین اولیه صحیح، از جواب واقعی دور خواهد بود. بنابراین، برای آنکه تخمین جواب، نزدیک به مقدار واقعی آن باشد، بعد از تخمین مقدار $$x$$ بر اساس حدس اولیه $$x _0$$، تابع را دوباره حول نقطه $$x$$ خطی می‌کنیم. این فرایند را تا جایی ادامه می‌دهیم که اختلاف بین تخمین فعلی و مقدار تخمینی قبلی، کمتر از یک مقدار مشخص از پیش تعیین شده باشد. این روش تکرار، «روش نیوتن-رافسون» (Newton-Raphson Method) نامیده می‌شود. معادله (۳) نیز به نام معادله نیوتن-رافسون شناخته می‌شود:

$$\large x _ { k + 1 } = x _ { k } + \left [ \frac { \partial f ( x _ k ) } { \partial x } \right ] ^ { - 1 } \left [ f ( x ) - f ( x _ k ) \right] \,\,\,\,\, (3)$$

که در آن، $$k=0, 1, 2, \cdots$$ عدد تکرار فعلی است.

مثال ۲

مقدار $$x$$ را با استفاده از روش نیوتن-رافسون به گونه‌ای محاسبه کنید که رابطه $$f (x ) = 103$$ برای تابع مثال قبل برقرار باشد. حدس اولیه را $$x _0 =-1$$ در نظر بگیرید.

حل: تابع و مشتق اول آن به صورت زیر هستند:‌

$$\large \begin {align*} f ( x ) & = 4 x _ { k } ^ { 2 } + 3 = 103 \\ \frac {\partial f ( x ) } { \partial x } & = 8 x \end {align*}$$

بنابراین، معادله نیوتن-رافسون به صورت زیر در خواهد آمد:‌

$$\large x _ { k + 1 } = x _ { k } + \frac { ( 1 0 3 - 4 x ^ { 2 } - 3 ) } { 8 x _ k }$$

با شروع از $$k = 0$$، می‌توانیم جواب $$x$$ را برای $$k+1$$ تخمین بزنیم. فرض می‌کنید خطای مورد نظر $$(x_{k+1} - x_k) \lt 0.00001$$ باشد.

مقادیر هشت تکرار اول به صورت زیر هستند:

$$\large \begin {align*} x _ 0 & = -1 \\ x _ 1 & = - 1 3 \\ x _ 2 & = - 7.46154 \\ x _ 3 & = - 5.40603 \\ x _ 4 & = - 5.01525 \\ x _ 5 & = - 5.00002 \\ x _ 6 & = - 5.00000 \\ x _ 7 & = - 5.00000 \end {align*}$$

همان‌طور که می‌بینیم، جواب بعد از تکرار $$k = 5$$ به مقدار $$x = -5.00$$ همگرا می‌شود و اختلاف آن با نتیجه حاصل از دو تکرار بعدی، کمتر از مقدار تلورانسی است که در نظر گرفته‌ایم. درستی جواب را می‌توان با قرار دادن آن در تابع تحقیق کرد.

عموماً معادلات غیرخطی چند جواب دارند و روش نیوتن-رافسون جوابی را به دست خواهد داد که به حدس اولیه نزدیک باشد. برای به دست آوردن سایر جواب‌ها باید مقدار اولیه را تغییر داد.

در مثال اخیر، اگر مقدار حدس اولیه را به $$x _ 0 = 1$$ تغییر دهیم، جواب با تکرارهای مشابهی همگرا خواهد شد، اما جهت آن مخالف بوده و جواب دوم $$x = 5$$‌ را نتیجه خواهد داد. وقتی حدس اولیه به جواب نزدیک باشد، روش نیوتن-رافسون به سرعت همگرا خواهد شد. البته در برخی شرایط، این روش واگرا شده یا اطلاعات صحیحی را از وجود جواب ارائه نمی‌کند. در مثال بالا، اگر $$f (x ) = 0$$ باشد، روش نیوتن-رافسون همگرا نمی‌شود.

از روش نیوتن-رافسون معمولاً برای یافتن ریشه یک تابع، یعنی حل معادله به شکل $$f (x ) =0$$ استفاده می‌شود. بنابراین، معادله (۳) را می‌توان به صورت زیر نوشت:

$$\large x _ { k + 1 } = x _ { k } - \left [ \frac { \partial f ( x _ k ) } { \partial x } \right ] ^ { - 1 } f ( x _ k )$$

روش نیوتن-رافسون چند بعدی

در بخش قبلی، از روش نیوتن-رافسون برای یافتن ریشه معادله $$f(x)$$ استفاده کردیم. حال فرض کنید بخواهیم مجموعه‌ای از $$n$$ معادله را به فرم $$\boldsymbol{F}(\boldsymbol{x})$$ حل کنیم.

فیلم آموزش بررسی سیستم‌ های قدرت ۱ – مرور و حل سوالات آزمون های استخدامی در فرادرس

کلیک کنید

در این صورت، معادله (۴) به فرم ماتریسی زیر در می‌آید:

$$\large \boldsymbol{ x } _ { k + 1 } = \boldsymbol { x } _ { k } - [ J ] ^ { - 1 } \boldsymbol { F } ( \boldsymbol { x } _ { k } )$$

فیلم آموزش بررسی سیستم های قدرت ۱ – مرور و حل تمرین در فرادرس

کلیک کنید

که در آن، $$\boldsymbol{x}$$ بردار $$n \times 1$$ ریشه‌های مجموعه توابع $$\boldsymbol{F}$$ است. ماتریسِ

$$\large [ J ] = \begin {bmatrix} \frac { \partial F _ 1 } { \partial x _ 1 } & \cdots & \frac { \partial F _ 1 } { \partial x _ n } \\ \vdots & \ddots & \vdots \\ \frac { \partial F _ m } { \partial x _ 1 } & \cdots & \frac { \partial F _ m } { \partial x _ n } \end {bmatrix}$$

یک ماتریس ژاکوبی $$n \times n$$ است.

پخش بار نیوتن رافسون

روش نیوتن-رافسون برای محاسبه بردار اندازه ولتاژ شین و زاویه آن‌ها به کار می‌رود:

$$\large \boldsymbol { x } = \begin {bmatrix} \boldsymbol { \delta } \\ \boldsymbol { | V | } \end {bmatrix}$$

در اینجا ذکر چند نکته لازم است:

1. ولتاژ‌ و زاویه شین مرجع، مشخص است و بنابراین، در بردار $$\boldsymbol{x}$$ وجود نخواهد داشت.
2. اندازه ولتاژ‌ باس‌های PV مشخص است و بنابراین، در $$\boldsymbol{|V|}$$ وجود ندارند. تنها، اندازه ولتاژ‌ شین‌های PQ در بردار وجود دارد.
3. زاویه $$\boldsymbol{\delta}$$ برای همه شین‌های PQ و PV در بردار $$\boldsymbol{x}$$ وجود خواهد داشت.

بنابراین، بردار $$\boldsymbol{x}$$، یک بردار $$m \times 1$$ است، که در آن:

$$\large m = 2 n _ { P Q } + n _ { P V }$$

جمله $$n_{PQ}$$ تعاداد شین‌های PQ و $$n_{PV}$$ تعداد شین‌های PV است.

دقت کنید که باید ابتدا شین‌های PQ و سپس شین‌های PV در بردار قرار گیرند.

الگوریتم پایه

معادله اساسی روش نیوتن-رافسون به صورت زیر است:

$$\large \begin {bmatrix} \boldsymbol { \delta } _ { k + 1 } \\ \boldsymbol { | V | } _ { k + 1 } \end {bmatrix} = \begin {bmatrix} \boldsymbol { \delta } _ { k } \\ \boldsymbol { | V | } _ { k } \end {bmatrix} - [ J ] ^ { - 1} \begin {bmatrix} \Delta \boldsymbol { P } _ { k } \\ \Delta \boldsymbol { Q } _ { k } \end {bmatrix}$$

که در آن، پارامترها به صورت زیر هستند:

• $$\boldsymbol{\delta}_{k}$$ بردار زاویه ولتاژ‌ شین‌ها در تکرار $$k$$اُم
• $$\boldsymbol{|V|}_{k}$$ بردار اندازه ولتاژ شین‌ها در تکرار $$k$$اُم
• $$\Delta \boldsymbol { P } _ { k } = \boldsymbol { P } _ { s p e c } - \boldsymbol { P } _ { c a l c } ( \boldsymbol { \delta } _ { k } , \boldsymbol { | V | } _ { k } )$$ بردار اختلاف توان اکتیو تزریقی تعیین شده و محاسبه شده (با استفاده از اندازه ولتاژ‌ شین‌ها و زاویه آن‌ها در تکرار $$k$$اُم)
• $$\Delta \boldsymbol { Q } _ { k } = \boldsymbol { Q } _ { s p e c } - \boldsymbol { Q } _ { c a l c } ( \boldsymbol { \delta } _ { k } , \boldsymbol { | V | } _ { k } )$$ بردار اختلاف توان راکتیو تزریقی تعیین شده و محاسبه شده (با استفاده از اندازه ولتاژ‌ شین‌ها و زاویه آن‌ها در تکرار $$k$$اُم)

ماتریس ژاکوبی

طبق قرارداد، ماتریسی ژاکوبی به فرم ماتریس تقسیم شده زیر تشکیل می‌شود:

$$\large [ J ] = \left [ \begin {matrix} \frac { \partial \boldsymbol { P } } { \partial \boldsymbol { \delta } } & | & \frac { \partial \boldsymbol { P } } { \partial \boldsymbol { V } } \\ ---- & | & ---- \\ \frac { \partial \boldsymbol { Q} } { \partial \boldsymbol { \delta } } & | & \frac { \partial \boldsymbol { Q } } { \partial \boldsymbol { V } } \end {matrix} \right]$$

که در آن، مثلاً‌ زیرماتریس $$\frac { \partial \boldsymbol { P } } { \partial \boldsymbol { \delta } }$$ به صورت زیر است:

$$\large \frac { \partial \boldsymbol { P } } { \partial \boldsymbol { \delta } } = \left [ \begin {matrix} \frac { \partial P _ { 1 } } { \partial \delta _ { 1 } } & \frac { \partial P _ { 1 } } { \partial \delta _ { 2 } } & \cdots & \frac { \partial P _ { 1 } } { \partial \delta _ { n } } \\ \frac { \partial P _ { 2 } } { \partial \delta _ { 1 } } & \ddots & & \vdots \\ \vdots & & \ddots & \vdots \\ \frac { \partial P _ { m } } { \partial \delta _ { 1 } } & \cdots & \cdots & \frac { \partial P _ { m } } { \partial \delta _ { n } } \end {matrix} \right ]$$

سه ماتریس دیگر نیز مشابه ماتریس بالا محاسبه می‌شوند.

چهار زیرماتریس اعدادی شامل اعدای حقیقی هستند که مطابق زیر محاسبه می‌شوند:

(الف) زیرماتریس $$\large \frac { \partial \boldsymbol { P } } { \partial \boldsymbol { \delta } }$$:

$$\large \begin {align*} \frac { \partial P _ { i } } { \partial \delta _ { i } } & = \sum _ { k = 1 , k \neq i } ^ { n } | V _ { i } | | V _ { k } | \left [ B _ { i k } \cos ( \delta _ { i } - \delta _ { k } ) - G _ { i k } \sin ( \delta _ { i } - \delta _ { k } ) \right ] \\ & = - Q _ { i } - B _ { i i } V _ { i } ^ { 2 } \\ \frac { \partial P _ { i } } { \partial \delta _ { k } } & = | V _ { i } | | V _ { k } | \left [ G _ { i k } \sin ( \delta _ { i } - \delta _ { k } ) - B _ { i k } \cos ( \delta _ { i } - \delta _ { k } ) \right ] \end {align*}$$

(ب) زیرماتریس $$\large \frac { \partial \boldsymbol { Q } } { \partial \boldsymbol { \delta } }$$:

$$\large \begin {align*} \frac { \partial Q _ { i } } { \partial \delta _ { i } } & = \sum _ { k = 1 , k \neq i } ^ { n } | V _ { i } | | V _ { k } | \left [ G _ { i k } \cos ( \delta _ { i } - \delta _ { k } ) + B _ { i k } \sin ( \delta _ { i } - \delta _ { k } ) \right ] \\ & = P _ { i } - G _ { i i } V _ { i } ^ { 2 } \\ \frac { \partial Q _ { i } } { \partial \delta _ { k } } & = - | V _ { i } | | V _ { k } | \left [ G _ { i k } \cos ( \delta _ { i } - \delta _ { k } ) + B _ { i k } \sin ( \delta _ { i } - \delta _ { k } ) \right ] \end {align*}$$

(ج) زیرماتریس $$\large \frac { \partial \boldsymbol { P } } { \partial \boldsymbol { | V | } }$$:

$$\large \begin {align*} V _ { i } \frac { \partial P _ { i } } { \partial | V _ { i } |} & = \sum _ { k = 1 , k \neq i } ^ { n } | V _ { i } | | V _ { k } | \left [ G _ { i k } \cos ( \delta _ { i } - \delta _ { k } ) + B _ { i k } \sin ( \delta _ { i } - \delta _ { k } ) \right ] + 2 G _ { i i } | V _ { i } | ^ { 2 } \\ & = P _ { i } + G _ { i i } V _ { i } ^ { 2 } \\ V _ { k } \frac { \partial P _ { i } } { \partial | V _ { k } | } & = | V _ { i } | | V _ { k } | \left [ G _ { i k } \cos ( \delta _ { i } - \delta _ { k } ) + B _ { i k } \sin ( \delta _ { i } - \delta _ { k } ) \right ] \end {align*}$$

(د) زیرماتریس $$\large \frac { \partial \boldsymbol { Q } } { \partial \boldsymbol { | V | } }$$:

$$\large \begin {align*} V _ { i } \frac { \partial Q _ { i } } { \partial | V _ { i } |} & = \sum _ { k = 1 , k \neq i } ^ { n } | V _ { i } | | V _ { k } | \left [ G _ { i k } \sin ( \delta _ { i } - \delta _ { k } ) - B _ { i k } \cos ( \delta _ { i } - \delta _ { k } ) \right] - 2 B _ { i i } | V _ { i } | ^ { 2 } \\ & = Q _ { i } - B _ { i i } V _ { i } ^ { 2 } \\ V _ { k } \frac { \partial Q _ { i } } { \partial | V _ { k } | } & = | V _ { i } | | V _ { k } | \left [ G _ { i k } \sin ( \delta _ { i } - \delta _ { k } ) - B _ { i k } \cos ( \delta _ { i } - \delta _ { k } ) \right] \end {align*}$$

بدحالت بودن

اگر ماتریس ژاکوبی بدحالت باشد، مسئله پخش بار بدحالت (Ill-Conditioned) نامیده می‌شود. این موضوع به این دلیل است که در الگوریتم نیوتن-رافسون، هر تکرار به فرم خطی زیر است:

$$\large [ J ] \Delta \boldsymbol { x } = - \Delta \boldsymbol { S }$$

که در آن، پارامترها به صورت زیر هستند:

• $$[J]$$ ماتریس ژاکوبی پخش بار
• $$\Delta \boldsymbol { x } = \begin {bmatrix} \boldsymbol { \delta } _ { k + 1} \\ \boldsymbol { | V | } _ { k + 1 } \end {bmatrix} - \begin {bmatrix} \boldsymbol { \delta } _ { k } \\ \boldsymbol { | V | } _ { k } \end{bmatrix}$$ بردار تصحیح اندازه و زاویه ولتاژ
• $$\Delta \boldsymbol { S } = \begin {bmatrix} \Delta \boldsymbol { P } _ { k } \\ \Delta \boldsymbol { Q } _ { k } \end {bmatrix}$$ بردار اختلاف مربوط به توان اکتیو و توان راکتیو است.

بنابراین، اگر ماتریس ژاکوبی بدحالت باشد، جواب پخش بار سیستم، ناپایدار یا واگرا خواهد بود.

مشخصه‌های اصلی که سبب بدحالت شدن مسئله پخش بار می‌شوند، به شرح زیر هستند:

• سیستم زیر بار زیاد (یعنی مسئله پایداری ولتاژ که در آن، سیستم به نقطه دماغه منحنی PV می‌رسد)
• خط‌های با نسبت $$R/X$$ بالا
• سیستم بزرگ با خطوط شعاعی زیاد
• انتخاب اشتباه شین مرجع

ویژگی‌های روش نیوتن-رافسون

بدون شک، الگوریتم نیوتن-رافسون، به دلیل ویژگی‌هایی که دارد، پراستفاده‌ترین روش پخش بار است:

• ویژگی همگرایی و دقت: الگوریتم نیوتن-رافسون همگرایی مربعی دارد و در اغلب سیستم‌های عملی، پس از ۵ تکرار و با دقت بالایی به جواب می‌رسد.
• سرعت: با استفاده از تکنیک‌های عددی می‌توان محاسبات مربوط به الگوریتم نیوتن-رافسون را نسبت به محاسبات دیگر، مؤثرتر کرد.
• قابلیت اطمینان: این الگوریتم بسیار قابل اطمینان بوده و قادر است سیستم‌های زیر بار زیاد را که نزدیک افت ولتاژ کار می‌کنند، حل کند.
• انعطاف‌پذیری: الگوریتم نیوتن-رافسون پایه را می‌توان برای تغییر تپ ترانسفورماتورها، ادوات FACTS و سایر تجهیزات راکتیو، سیستم‌های DC، ترانسفورماتورهای شیفت فاز و... گسترش داد.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• آموزش نرم‌ افزار DIgSILENT برای آنالیز و شبیه سازی سیستم های قدرت
• پایداری سیستم قدرت — به زبان ساده
• آشنایی با ترانسفورماتورها — مجموعه مقالات جامع وبلاگ فرادرس

^^