منحنی ROC در SPSS — راهنمای کاربردی

یکی از فنون ارزیابی نتایج حاصل از طبقهبندی (Categorized)، استفاده از منحنی ROC است. در تحلیل ROC، یک متغیر با دو مقدار وجود دارد که هر یک از آنها نشانگر تعلق مشاهدات به دسته یا گروه خاصی هستند. به این ترتیب یک «دستهبندی باینری» (Binary Classification) صورت میگیرد. از آنجایی که قانون تعلق مشاهدات جدید به هر یک از گروهها، بواسطه مثالهایی از مشاهدات قبلی ایجاد میشود، «ردهبندی» (Classification) را یک روش «یادگیری ماشین نظارتی» (Supervised Machine Learning) در نظر میگیرند. در این نوشتار به بررسی نحوه ارزیابی ردهبندی با استفاده از منحنی ROC در SPSS خواهیم پرداخت.
به منظور آشنایی بیشتر با اصطلاحات و نحوه ترسیم منحنی ROC، بهتر است نوشتارهای منحنی ROC و کاربردهای آن — به زبان ساده و ماتریس درهم ریختگی (Confusion Matrix) — از صفر تا صد را مطالعه کنید. همچنین خواندن مطالب روش های متن کاوی — راهنمای کاربردی و دسته بند بیز ساده (Naive Bayes Classifiers) — مفاهیم اولیه و کاربردها نیز خالی از لطف نیست.
منحنی ROC در SPSS
منحنی ROC یا به عبارتی منحنی «مشخصه عملکرد سیستم» (Receiver Operating Characteristics)، ابزاری برای نمایش دقت و کارایی یک تکنیک ردهبندی یا دستهبندی است. نحوه ارزیابی در منحنی مشخصه عملکرد، به شیوهای است که براساس نمونههایی که دسته یا ردههای آنها مشخص است، اقدام کرده و نتیجه دستهبندی الگوریتم ردهبندی را با دسته یا «ردههای واقعی» (Golden Standard) مقایسه میکند.
تعداد حالاتی که تشخیص رده به درستی یا نادرستی صورت گرفته، مبنایی برای محاسبه نواحی مختلف در منحنی ROC است. شیوه ترسیم و شاخصهای محاسباتی در منحنی ROC را میتوانید در اینجا مطالعه کنید. در این متن قرار است به کمک مثالهایی در محیط نرمافزار محاسبات آماری SPSS، چنین منحنی را ترسیم کنیم. به منظور ایجاد انگیزه بیشتر با استفاده از مثالهایی به نحوه تفسیر و استفاده از منحنی مشخصه عملکرد میپردازیم، در این بین رسم منحنی ROC در SPSS را فرا گرفته و تفسیر خروجیهای حاصل را مشخص میکنیم.
مثال ۱: منحنی ROC در SPSS و کاربرد آن در پزشکی
یک آزمایشگاه داروسازی در تلاش است تا یک روش سریع را برای تشخیص عفونت یا بیماری HIV ایجاد کند. تأخیر در به دست آوردن نتایج حاصل از آزمایشهای سنتی و قدیمی، باعث کاهش اثربخشی آنها میشود زیرا بسیاری از بیماران به منظور دریافت نتیجه آزمایش مراجعه نمیکنند در نتیجه زمان پاسخدهی در پیگیری بیماری بسیار مهم است.
در اینجا هدف، ایجاد آزمون پزشکی خاصی است که نتایج را در 10 تا 15 دقیقه ارائه داده و به اندازه تستهای جاری، دقیق باشد. شرکتی ادعا میکند یک برگه آزمایشی ساخته است که با استفاده از سطوح مختلف رنگ قرمز، تشخیص عفونت HIV را میسر ساخته. هر چه رنگ قرمز این برگه، پر رنگتر باشد، احتمال ابتلا به بیماری HIV بیشتر است. واضح است که این روش تشخیصی، بسیار سریع بوده و با سرعت نتیجه را اعلام میکند. سوال این است که آیا واقعا این روش، دارای دقت مناسب و قابل مقایسه با روش آزمایشهای قدیمیتر نیز هست؟
در اینجا ترسیم منحنی ROC میتواند ملاکی برای ارزیابی عملکرد و نمایش صحت روش آزمایش جدید باشد. به این منظور شرکت تولید کننده کیت تشخیصی، دست به انجام آزمایشی با ۲۰۰۰ نمونه از افراد واجد شرایط میزند. نیمی از این افراد پاک و نیم دیگر نیز براساس نتیجه آزمایش اصلی (روش قدیمی و زمان بر) HIV آنها مثبت بوده است.
فایل اطلاعاتی مربوط به نتیجه آزمایش جدید و قدیم برای این افراد در فایلهای آموزشی SPSS وجود دارد. کافی است از مسیر زیر به این فایل دسترسی پیدا کنید. البته فرض بر این است که نرمافزار SPSS در درایو C کامپیوتر شما نصب شده باشد.
C:\Program File\IBM\SPSS\Statistics\26\sample\English\hivassay.sav
اگر امکان دسترسی به این فایل از طریق پوشه SPSS فراهم نیست، میتوانید فایل hivassay.sav را با قالب فشرده از اینجا دریافت کرده و پس از خارج کردن از فشردگی، در برنامه SPSS باز کرده و مورد استفاده قرار دهید. در تصویر ۲، نمونهای از اطلاعات مربوط به این فایل داده را مشاهده میکنید.
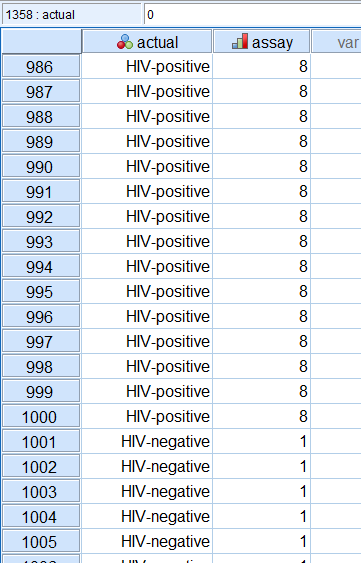
همانطور که در تصویر ۲، مشاهده میکنید، براساس متغیر actual، هزار نفر اول براساس آزمایش اولیه، بیمار تشخیص داده شده و هزار نفر دوم آزمایش آنها منفی بوده و بیمار تشخیص داده نشدهاند. در ستون دوم یعنی assay اما، نتایج آزمایش جدید شرکت تولید کننده کیت تشخیصی، مورد توجه بوده و براساس درجههای رنگ قرمز، مقادیری از ۱ تا ۸ حاصل شده است. قرار است پزشکان به کمک منحنی ROC نقطه برش (Cutoff) برای تشخیص بیمار بودن افراد را با در نظر گرفته درجه رنگ قرمز مشخص کنند. به این ترتیب آستانه مقدار شدت رنگ قرمز توسط منحنی ROC تعیین کننده تشخیص HIV-Positive برای پزشکان خواهد شد.
مراحل زیر برای ایجاد یا رسم منحنی ROC در SPSS را برای این فایل داده طی خواهیم کرد.
- مسیر زیر را برای ظاهر کردن پنجره گفتگوی ROC Curve طی کنید.
Analyze > Classify > ROC Curve...
- تنظیمات را مطابق با تصویر ۳ یا جدول ۱ انجام دهید.
- دکمه OK را کلیک کنید تا در خروجی، منحنی ROC و شاخصهای آماری درخواستی ظاهر شوند.
به منظور رسم نمودار برای مجموعه داده hivassay، با انتخاب دستورات گفته شده، پنجرهای ظاهر شده که تنظیم پارامترهای آن را مانند تصویر ۳ اجرا میکنیم. واضح است که متغیر مورد بررسی همان assay با برچسب Assay Result بوده و متغیری که باید به عنوان وضعیت جاری و استاندارد در نظر گرفته شود، نیز Actual با برچسب Actual state است. نحوه قرارگیری هر یک از این متغیرها در تصویر ۳ دیده میشود.
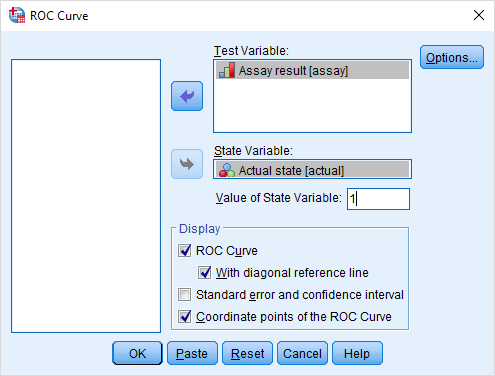
جدول ۱، به معرفی پارامترهای پنجره گفتگوی رسم منحنی ROC در SPSS پرداخته است.
جدول ۱: گزینه و پارامترهای رسم منحنی ROC در SPSS
| گزینه | عملکرد | شرح |
| Test Variable | متغیر مورد آزمایش | متغیری که قرار است مقدار آستانه برایش در ردهبندی مشخص شود. |
| State Variable | متغیر وضعیت | متغیری که وضعیت موجود و استاندارد را با توجه به دو مقدار ۰ یا ۱ مشخص کرده است. |
| Value of State Variable | مقدار مطلوب متغیر وضعیت | مقداری که به واسطه آن، گروه مورد نظر توسط متغیر وضعیت مشخص میشود. |
| ROC Curve | منحنی ROC | انتخاب این گزینه باعث ترسیم منحنی ROC میشود. |
| With diagonal reference line | رسم منحنی ROC به همراه خط قطری | نمایش خط قطری ناحیه مطلوب و نامطلوب را در منحنی ROC از یکدیگر جدا میکند. |
| Standard error and confidence interval | نمایش خطای استاندارد و فاصله اطمینان در منحنی ROC | |
| Coordinate points of the ROC Curve | نمایش جدول مختصات نقاط مربوط به مشاهدات در منحنی ROC | جدول حاصل مختصات هر نقطه از مشاهدات را برحسب حساسیت و ویژگی نمایش میدهد. |
البته دکمه Options در پنجره مربوط به تصویر ۳، تنظیمات بیشتری را هم فراهم میآورد که توضیحات مربوط به آنها در انتهای متن قرار دارد.
نکته: اگر میخواهید در محیط دستوری Syntax، فرمان رسم منحنی ROC در SPSS را صادر کنید، قطعه کد زیر مناسب است.
1ROC assay BY actual (1)
2 /PLOT=CURVE(REFERENCE)
3 /PRINT=SE COORDINATES
4 /CRITERIA=CUTOFF(INCLUDE) TESTPOS(LARGE) DISTRIBUTION(FREE) CI(95)
5 /MISSING=EXCLUDE.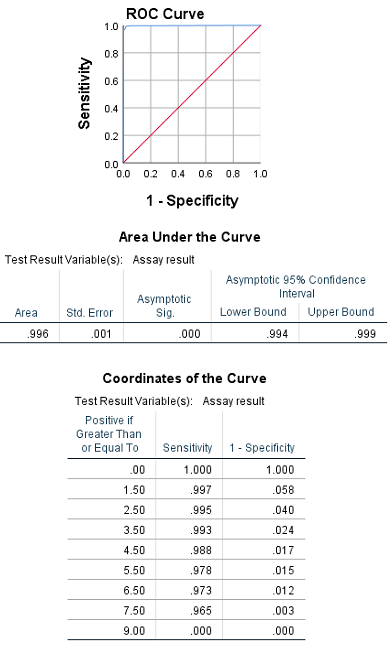
همانطور که مشخص است، ابتدا منحنی ROC رسم شده و در جدول بعدی نیز ناحیه زیر منحنی ROC به نام AUC مشخص شده. همچنین «انحراف استاندارد خطا» (Std. Error)، «مقدار احتمال مجانبی» (.Asymptotic Sig) یا همان p-value و «فاصله اطمینان مجانبی» (Asymptotic 95% Confidence Interval) را مشاهده میکنید. در انتها نیز جدول مربوط به نقطههای ترسیم شده در منحنی ROC را مشاهده میکنید.
همانطور که مشخص است مقدار «حساسیت» (Sensitivity) که محور عمودی و (ویژگی) و محور افقی را تشکیل میدهند به ترتیب در بازه و تغییر میکنند، پس بهتر است برای نمایش بهتر منحنی ROC، محورها را بر اساس این مقادیر محدود کنیم.
به این منظور ابتدا روی منحنی دوبار کلیک کرده تا به محیط ویرایش نمودار SPSS وارد شویم. گامهای زیر را به منظور نمایش بهتر نمودار ROC بر خواهیم داشت.
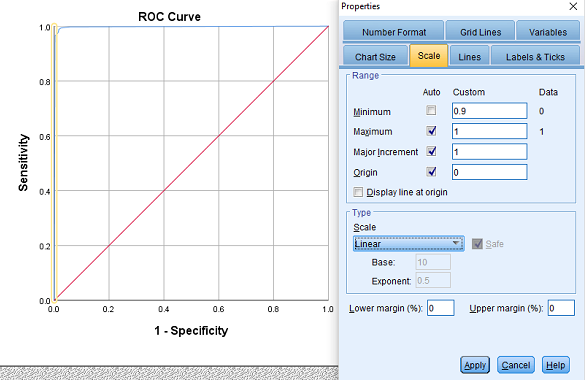
- روی محور عمودی در نمودار کلیک کرده و از پنجره Properties، برگه Scale را انتخاب و مقیاس را برای حداقل (Minimum) مقدار، 0.9 در نظر گرفته و دکمه Apply را کلیک میکنیم. پنجره تنظیمات مربوط به محورها در تصویر ۵ دیده میشود.
- روی محور افقی در نمودار کلیک کرده و برگه Scale را انتخاب و مقیاس را برای حداکثر (Maximum) مقدار، 0.06 در نظر میگیریم. با فشردن دکمه Apply این مقدار را ثبت میکنیم.
- با بستن پنجره Chart Editor، نموداری ثبت شده در پنجره خروجی مطابق با مقیاسهای شما در خواهد آمد.
در تصویر ۶، نتیجه انجام مراحل قبل را مشاهده میکنید.
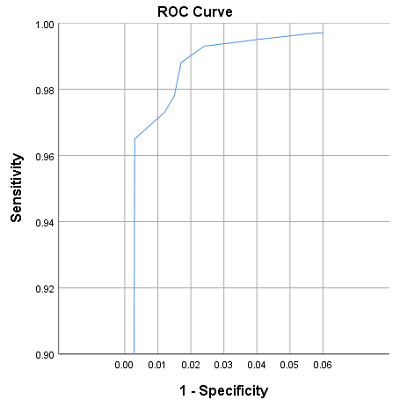
نکته: به علت تغییر مقیاس در منحنی مربوط به تصویر ۵، خط قطری، دیده نمیشود.
تفسیر منحنی ROC در SPSS برای «مثال ۱»
«مساحت زیر منحنی» (Area Under the Curve) یا به اختصار (AUC)، نشان میدهد که نتیجه سنجش برای یک مورد مثبت که البته به طور تصادفی انتخاب شده است، با چه احتمالی نتیجه را برای یک مورد منفی به طور تصادفی افزایش میدهد. از طرفی، مقدار p-value یا همان «سطح با معنایی» (.Sig) کمتر از 0.05 است، به این معنی که استفاده از روش آزمایش جدید نسبت به انتخاب تصادفی بهتر عمل کرده است.
در حالی که ناحیه زیر منحنی، یک شاخص آماری مفید از صحت سنجش و ارزیابی محسوب میشود، باید بتوان ملاک خاصی را انتخاب کرد که با استفاده از آن نمونههای آزمایش شده (با روش جدید) را به دو رستهها (بیمار و سالم) طبقه بندی کرد. به منظور بررسی نقاط برش یا آستانه، جدول «مختصات منحنی» (Coordinate of the Curve) را در تصویر ۴، مشاهده کنید.
در این جدول میزان «حساسیت» و «ویژگی - 1» برای هر برش احتمالی برای طبقهبندی مثبت (بیمار بودن با کد ۱) گزارش شده است. در اینجا «حساسیت» بر اساس کسر زیر محاسبه محاسبه میشود.
- صورت کسر: تعداد افرادی که HIV مثبت داشتهاند (با توجه به روش قدیمی و قطعی)
- مخرج کسر: تعداد افرادی که با توجه به بزرگتر بودن مقدار نتیجه آزمایش از مقدار ستون اول (...Positive) در آزمایش جدید، بیمار تشخیص داده شدهاند. مقادیر ستون اول به عنوان Cutoff فرض شدهاند.
از طرفی «ویژگی - ۱» () نیز به شکل یک کسر با صورت و مخرجی که در زیر مشاهده میکنید، در نظر گرفته میشود.
- صورت کسر: تعداد افرادی با HIV منفی براساس روش قدیمی و قطعی
- مخرج کسر: تعداد افرادی که با توجه به بزرگتر بودن مقدار نتیجه آزمایش از سطح آستانه (Cutoff) بیمار تلقی شدهاند.
نقطه برش صفر، معادل با فرض کردن آن است که طبق آزمایش جدید، همه HIV-positive هستند. همچنین نقطه برش 9.0 نیز بیانگر HIV-negative بودن افراد است. واضح است که این دو نقطه برش، غیرکاربردی هستند. هدف پیدا کردن مقدار در بین این دو است که نشانگر بیشتر بودن حساسیت و ویژگی باشند. در حقیقت به دنباله نقطهای هستیم که علاوه بر بزرگترین مقدار روی محور عمودی، کمترین مقدار روی محور افقی را هم دارا باشد.
برای مثال نقطه برش 5.5 را در نظر بگیرید. با در نظر گرفتن این مقدار آستانه، مقادیر ۶، ۷ و ۸ در نتیجه آزمایش جدید، بیانگر نتیجه مثبت آزمایش یعنی بیمار بودن فرد خواهد بود. براساس این آستانه، میزان «حساسیت» برابر با 0.978 بوده و مقدار «ویژگی - ۱» نیز 0.015 است. در نتیجه شیوه آزمایش جدید، در 97.8 درصد از مواقع آزمایش فرد بیمار را به درستی تشخیص داده است و در 1.5 درصد از موارد نیز کسی که بیمار نیست را به غلط، بیمار تعیین کرده است.
حال مقدار آستانه را برای نتیجه آزمایش جدید و طبقهبندی افراد به دو گروه بیمار و سالم، 2.5 فرض میکنیم. به این ترتیب با احتمال 99.5 درصد، تشخص صحیح صورت گرفته و فرد بیمار توسط آزمایش شناسایی شده است. از طرفی خطای این روش تشخیصی برای کسانی که بیمار نیستند برابر با 4 درصد است. یعنی فرد سالم با احتمال چهار صدم، در گروه بیماران طبقهبندی میشود.
انتخاب نقطه برش یا آستانه، با توجه به مقدار حساسیت و ویژگی آزمایش صورت میگیرد. توجه داشته باشید که مقادیر موجود در این جدول فقط راهنمایی برای تعیین آستانه محسوب میشود زیرا حاوی مقادیری مانند تخمین خطای برآورد نیست. بنابراین هیچ تضمینی برای تشخیص دقیق «حساسیت» یا «ویژگی» برای نقطه برش تعیین شده، در جدول وجود ندارد.
مثال ۲: منحنی ROC در SPSS و کاربرد آن در علوم بانکی
یکی از نیازهای بانک، شناسایی مشتریان است که به موقع وامهای خود را پس میدهند. اگر بانک بتواند روشی برای ردهبندی مشتریان ابداع کند که به کمک آن تشخیص دهد یک مشتری با چه خصوصیاتی، به عنوان مشتری خوب ردهبندی میشود، قادر است، برای جذب مشتریان جدید، از همان خصوصیات بهره گرفته و تقریبا مطمئن باشد که آنها، در پرداخت وامها، بانک را دچار مشکل نمیکنند. رسم منحنی ROC برای نمایش و ارزیابی نتیجه به کارگیری «الگوریتم ردهبندی» (Classification Algorithm) یکی از تکنیکهای مقایسه این گونه الگوریتمها خواهد بود.
فرض کنید یک بانک معروف، با در نظر گرفتن یک جایزه، برنامهنویسان و «تحلیلگران داده» (Data Scientist) را تشویق به ابداع الگوریتم تشخیص مشتری خوب کرده است. در این بین سه روش یا الگوریتم قابل استفاده تشخیص داده شدهاند. بانک میخواهد کارایی این سه روش را بسنجد. به این منظور برای ارزیابی آنها، از منحنی ROC استفاده کرده است.
ما هم به همین صورت برای نشان دادن دقت و صحت عملکرد سه الگوریتم ردهبندی، از منحنی ROC در SPSS براساس یک فایل داده آموزشی به نام bankloan.sav استفاده میکنیم. دسترسی به این فایل درست به مانند مثال قبل صورت میگیرد. در تصویر 7، نمونهای از مشاهدات مربوط به این فایل را مشاهده میکنید.
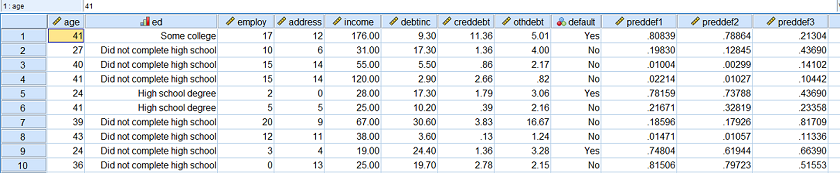
همانطور که در تصویر ۷ مشاهده میکنید، ۱۲ متغیر معرفی شدهاند که سه متغیر آخر، نتیجه اجرای سه الگوریتم متفاوت برای تشخیص مشتریان بانک است. وضعیت مشتری نسبت به وام دریافتی (واقعیت) در متغیر default ثبت شده است. واضح است که الگوریتمها براساس هشت متغیر اول (age, ed, employ, address, income, debtinc, creddebt, othdebt) به عنوان متغیر پیشگو و متغیر نهم (default) به عنوان متغیر وابسته عمل کردهاند و نتیجه ردهبندی یا امتیاز ردهبندی برای سه الگوریتم نیز در سه متغیر آخر قرار گرفتهاند. به نوعی میتوان این مقادیر را احتمال قرارگیری مشتری در گروه مشتری خوب قلمداد کرد.
نکته: اگر امکان دسترسی به این فایل از طریق مسیر گفته شده مقدور نباشد، میتوانید فایل bankloan.sav را با قالب فشرده از اینجا دریافت کنید. به یاد داشته باشید که برای استفاده از این فایل، ابتدا آن را از حالت فشرده (zip) خارج کرده، سپس در SPSS بارگذاری کنید.
برای تشخیص الگوریتم برتر از بین سه الگوریتم معرفی شده، منحنی ROC را برایشان ترسیم میکنیم. به این منظور، تنظیمات مربوط به پارامترهای دستور رسم منحنی ROC در SPSS را مطابق با تصویر ۸ انجام میدهیم. همانطور که میبینید سه متغیر preddef2 ،preddef1 و preddef3 به عنوان متغیرهای آزمون (Test Variable) به کار رفته و State Variable نیز همان وضعیت جاری مشتریان یعنی متغیر default با برچسب Previously Defaulted تعیین شده است.
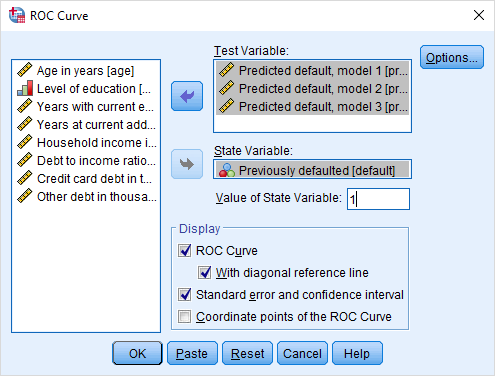
واضح است که طبقه یا دستهای که به دنبال مدلسازی آن هستیم، مقدار ۱ است که نشانگر وضعیت نامطلوب (default=1) مشتری در بازپرداخت وام است. به همین دلیل پارامتر Value of State Variable را برابر با ۱ قرار دادهایم.
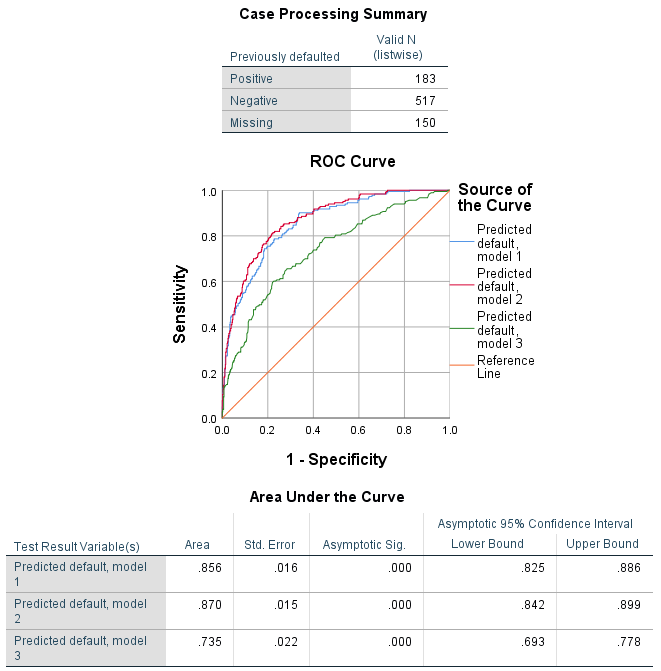
واضح است که سه منحنی به رنگهای قرمز، آبی و سبز در نمودار دیده میشوند که هر یک نماینده یکی از مدلهای ایجاد شده توسط متغیرهای preddef2 ، preddef1 و preddef3 هستند. معرفی هر یک از این متغیرها در بخش راهنمای نمودار در سمت راست منحنی دیده میشود.
تفسیر منحنی ROC در SPSS برای «مثال 2»
با توجه به فاصلهای که هر یک از این نمودارها با «خط قطری» (diagonal line) دارند، مشخص میشود که هر سه مدل، نسبت به انتخاب تصادفی، اولویت دارند. از طرفی با توجه به پوشش منحنی مربوط به مدل سوم (preddef3) توسط دو مدل دیگر، توجیهی برای استفاده از آن دیده نمیشود زیرا هم از لحاظ حساسیت و هم ویژگی، از دو مدل دیگر قابلیت کمتری دارد.
همچنین با در نظر گرفتن جدول انتهایی که مربوط به سطح زیر منحنی یا AUC است، مشخص میشود که برای هر سه مدل، سطح معنیداری مجانبی کمتر از 0.05 است. پس باز هم مشخص است که نسبت به حالت تصادفی، هر سه مدل در پیشبینی رفتار مشتری تفاوت معنیداری دارند.
از فواصل اطمینان (Confident Interval) در سطح ٪95 به صورت مجانبی، میبینید که مدل 3 نسبت به دو مورد دیگر به 0.5 که همان حدس تصادفی است نزدیکتر است. مدلهای 1 و 2 تقریباً قابل تشخیص نیستند، بنابراین مدلی به نظر مناسبتر میرسد که به متغیرها ورودی کمتری احتیاج دارد. به این ترتیب با ترسیم منحنی ROC در SPSS برای مقایسه سه مدل ردهبندی مختلف، استفاده کرده و این منحنی نمایش بصری بسیار خوبی از عملکرد مدلها ارائه میدهد.
نکته: در اینجا جدول «مختصات منحنی» (Coordinate of the Curve) چندان مفید به نظر نمیرسد، زیرا متغیرهای نتیجه آزمون متنوع و مقادیر زیادی دارند، بنابراین جدولی بسیار طولانی و ناخوشایند، حاصل خواهد شد.
با استفاده از جدول طبقهبندی، میتوان حساسیت و ویژگی را برای یک مقدار آستانه محاسبه کرد. البته در این مثال، آستانهها در منحنی ROC مشخص شده و قابل مشاهدهاند. به این ترتیب ROC Curve یک نمایش بصری از این کلیه نقاط برش در یک طرح واحد فراهم میکند که بسیار زیباتر و قدرتمندتر از جداول محسوب میشود.
تنظیمات مربوط به نحوه رسم منحنی ROC در SPSS
اگر برای ترسیم منحنی ROC، احتیاج به تنظیمات بیشتری دارید، بهتر است در پنجره اصلی، دکمه Options را کلیک کنید تا امکاناتی که در SPSS برای این منحنی در نظر گرفته شده، مطابق با تصویر ۱۰، ظاهر شوند.
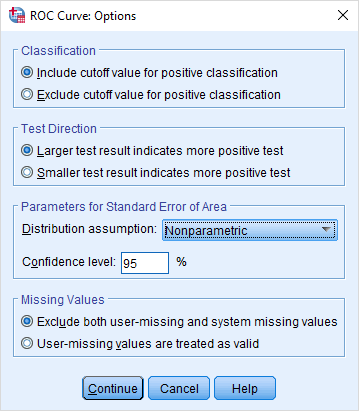
این تنظیمات در چهار بخش، تفکیک شدهاند. بخش اول مربوط به ردهبندی (Classification) مشاهدات با توجه به نقطه برش یا آستانه است. بخش دوم نیز جهت پاسخ آزمون (Test Direction) را مشخص میکند. برای تعیین توزیع آماری پارامترها و تعیین خطای استاندارد ناحیه زیر منحنی (Parameters for Standard Error of Area) نیز بخش سوم به کار میآید. بخش انتهایی و چهارم هم دادههای گمشده (Missing Values) در تحلیل را مدیریت میکند.
هر یک از امکانات و تنظیمات بخشهای ذکر شده در ادامه معرفی و توضیح داده میشوند.
- ردهبندی (Classification):
- با انتخاب گزینه Include cutoff value for positive classification، مقدار آستانه یا برش در گروه مثبت در نظر گرفته میشود.
- گزینه دوم یا ...Exclude cutoff value مقدار آستانه را در گروه مثبت، ردهبندی نمیکند.
- جهت آزمون (Test Direction): به کمک این گزینه جهت متغیر عددی را در رابطه با نتیجه رده مثبت، تعیین میکنید.
- با انتخاب گزینه Larger test result indicated more positive test، مشخص میکنید که مقادیر بزرگتر برای نتیجه آزمون، موید مثبت بودن بیشتر خواهد بود. این موضوع، در ستون اول جدول مختصات منحنی نیز به شکل (Positive if Greater Than or Equal To) نوشته شده است.
- گزینه دوم ...Smaller test به منزله کوچک بودن مقادیر نتایج آزمون با مثبت بودن بیشتر است. اگر این گزینه فعال شود، متن مربوط به ستون اول جدول (Coordinate of the Curve) تغییر خواهد کرد و به صورت (Positive if Less Than or Equal To) نمایش داده میشود.
- پارامترهای خطای استاندارد ناحیه زیر منحنی: این گزینه به شما امکان میدهد، روش تخمین خطای استاندارد ناحیه زیر منحنی را مشخص کنید.
- توزیع آماری میتواند یکی از حالتهای «ناپارامتری» (Nonparametric) یا «توزیع نمایی دو منفی» (Binegative Exponential) باشد.
- میزان یا سطح اطمینان برای «فاصله اطمینان» (Confidence Interval) دو طرفه AUC توسط گزینه Confidence level در این پنجره صورت گرفته و مقادیر آن از 0.0٪ تا 100.0٪ قابل تعیین هستند. مقدار پیش فرض 95٪ در نظر گرفته شده است.
- مشاهدات گمشده (Missing Values): تنظیمات معرفی شده در این بخش به کاربر امکان میدهد، نحوه برخورد با مقادیر از دست رفته یا گمشده (Missing Value) را مشخص کند.
- انتخاب گزینه Exclude both user-missing and system missing values، باعث میشود که منحنی ROC، مقادیر گمشده از نوع کاربر و سیستمی را به کار نبرد.
- با انتخاب User-missing values are treated as valid، مقادیر گمشده سیستمی در تحلیل حذف شده و فقط مقادیر گمشده که توسط کاربر تعیین شدهاند به عنوان دسته یا گروههای ردهبندی عمل کرده و در محاسبات معتبر هستند.
پس از انجام تنظیمات، با فشردن دکمه Continue به پنجره اصلی باز خواهید گشت و با کلیک روی دکمه OK در پنجره ROC Curve، رسم نمودار و جدولها در خروجی، صورت خواهد گرفت.
خلاصه و جمعبندی
در این نوشتار به بررسی نحوه تفسیر و توصیف نتایج حاصل از منحنی ROC در SPSS پرداختیم. همانطور که دیدید به کمک دو مثال، نحوه به کارگیری چنین نموداری را مشخص کردیم. در مثال اول به بررسی یک روش تشخیص پزشکی پرداختیم که در آن براساس منحنی ROC، مقدار آستانه یا نقطه برش را برای یک متغیر طبقهای با چند سطح، مشخص کردیم. در مثال دوم، در مورد نحوه طبقهبندی مشتریان بانک به دو گروه مشتریان خوب و بد براساس سه الگوریتم متفاوت دست به قضاوت زدیم. در اینجا نیز تفسیر منحنی ROC به انتخاب مدل مناسب با کمترین متغیرها و بهترین کارایی، کمک شایانی کرد.













بسيار عالي و كاربردي، ممنون از توضيحات خوبتان
سلام.
چقدر ساده و کامل و کاربردی بود.
بسیار سپاسگزارم
بسیارعالی. متشکر از آموزشهای سودمنددرزمینه آمار