رگرسیون لجستیک در پایتون – راهنمای گام به گام
یکی از تکنیکهای پیشرفته آماری که در «یادگیری ماشین» (Machine Learning) بسیار کاربرد دارد، «رگرسیون لجستیک» (Logistic Regression) است. در این روش رگرسیونی، «متغیر پاسخ» (Response Variable)، دارای دو مقدار یا دو طبقه است. معمولا این دو مقدار را با ۰ و ۱ نشان میدهند که ۰ بیانگر عدم حضور یک ویژگی خاص و ۱ نشانگر وجود آن ویژگی در مشاهده مورد نظر است.
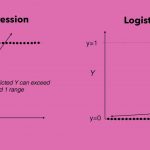
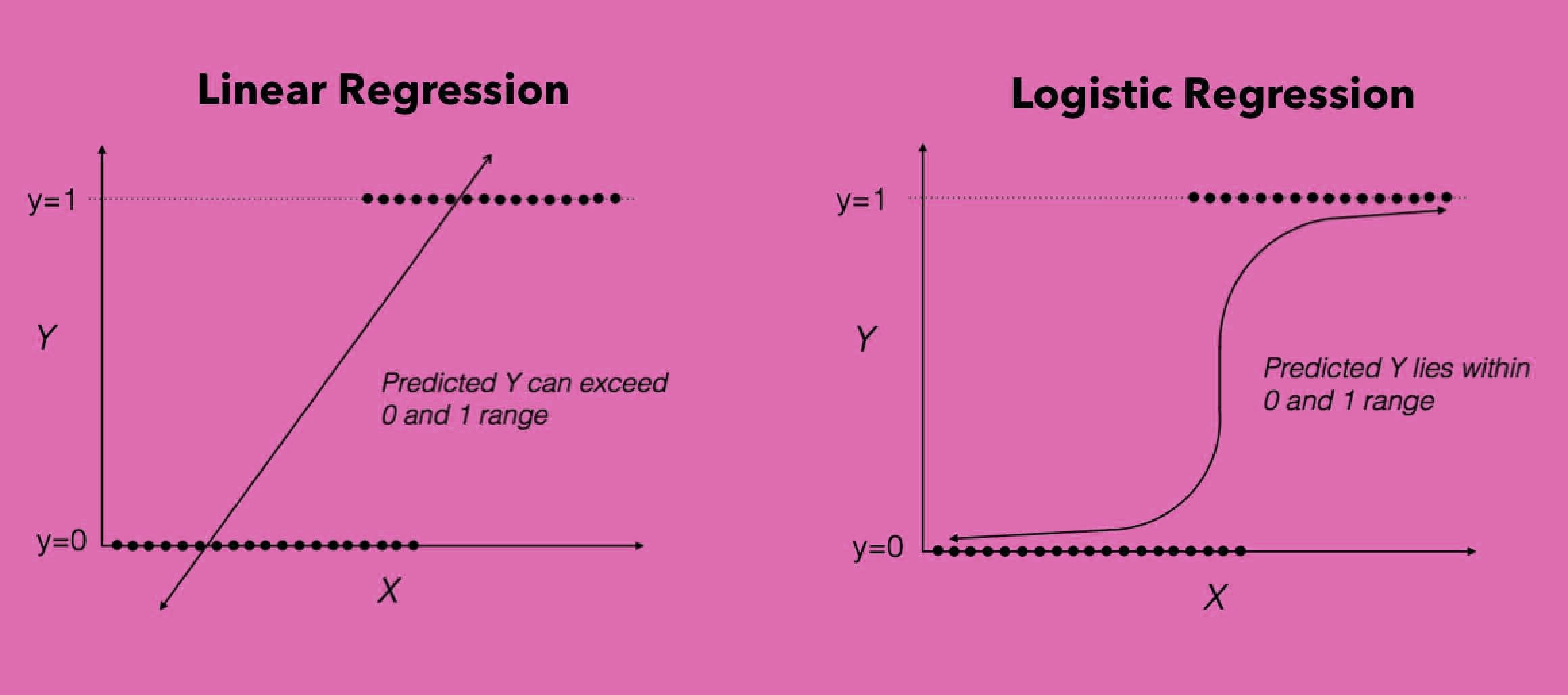
به این ترتیب اگر متغیر پاسخ را با Y و متغیر مستقل را با X نشان دهیم، رگرسیون لجستیک مقدار را محاسبه میکند که به معنی احتمال وجود ویژگی به شرط متغیر مستقل است. این احتمال یک تابع برحسب x است که به پیشبینی مقدار برچسب یک مشاهده برحسب مقدارهای متغیرهای مستقل میپردازد. این احتمال را گاهی درجه تعلق به گروه ۱ نیز مینامند.
در نتیجه رگرسیون لجستیک به عنوان ابزار «دستهبندی» (Classification) و تابع نیز یک «دستهبند» (Classifier) نامیده میشود. با ایجاد چنین مدلی، میتوان با اندازهگیری کردن متغیرهای مستقل برای یک مشاهده جدید درجه تعلق آن را به گروه ۱ پیشبینی کرد.
برای آشنایی بیشتر با مفاهیم و شیوه محاسبات رگرسیون لجستیک به مطلب رگرسیون لجستیک (Logistic Regression) — مفاهیم، کاربردها و محاسبات در SPSS مراجعه کنید. همچنین خواندن نوشتار رگرسیون خطی — مفهوم و محاسبات به زبان ساده نیز خالی از لطف نیست.
رگرسیون لجستیک در پایتون
از رگرسیون لجستیک برای تحلیل رابطه بین متغیرها بخصوص در زمینههای پزشکی، روانشناسی، علوم اجتماعی و تبلیغات بسیار کمک گرفته میشود. برای مثال بررسی و ایجاد مدل رابطه بین ویژگیهای مشتریان بانک به عنوان متغیرهای مستقل و پذیرش در باز کردن حساب سپرده طولانی مدت به عنوان متغیر پاسخ بوسیله رگرسیون لجستیک صورت میگیرد. مشخص است که متغیر پاسخ دارای دو سطح ۰ (عدم پذیرش) و ۱ (پذیرش) است. متغیرهای مستقل نیز میتوانند سن، شغل، وضعیت تاهل، میزان تحصیلات، تراز یا گردش حساب جاری و درآمد باشد.
در ادامه به بررسی یک مثال واقعی در این زمینه میپردازیم. دادههای مربوط به این مثال اطلاعات جمعآوری شده یک بانک در کشور پرتقال است. برای دریافت این دادهها میتواند به این اینجا مراجعه کنید. در این فایل اطلاعات 41188 مشتری با ۲۰ ویژگی متفاوت جمعآوری شده است. همچنین در ستون آخر مقدار متغیر y نیز به عنوان متغیر پاسخ ثبت شده.
برای شروع کار، ابتدا کتابخانههای مورد نیاز برای پایتون را بارگذاری میکنیم، سپس به بررسی دادهها میپردازیم.
در تصویر زیر بعضی از مشاهدات مربوط به این فایل اطلاعاتی دیده میشود. مشخص است که این دادهها با قالب CSV (جدا شده بوسیله کاما) ثبت شده است.
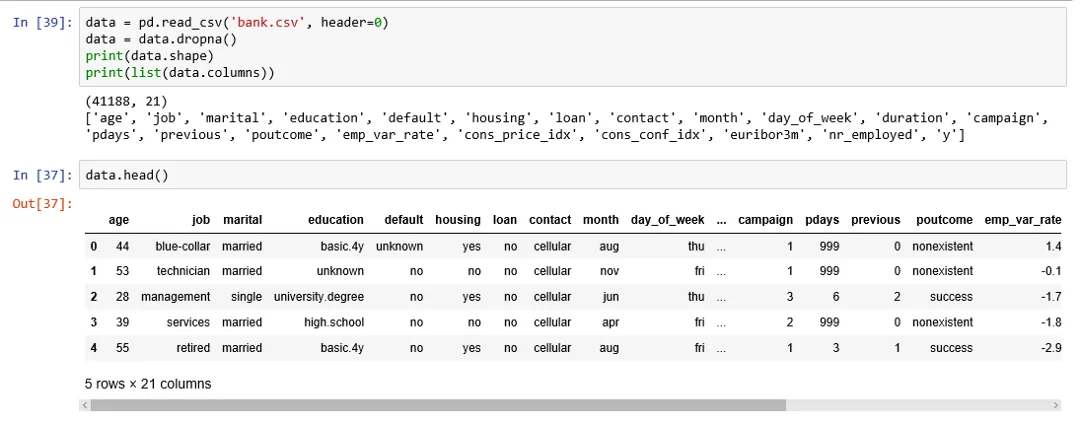
به منظور اجرای رگرسیون لجستیک، باید فرضیات زیر محقق شوند.
- دادههای متغیر پاسخ باید به صورت باینری (دو دویی) باشند.
- مقدار ۱ در متغیر پاسخ نشانگر مقدار مورد انتظار است. به این ترتیب رگرسیون لجستیک مقدار را برآورد میکند.
- برای ایجاد مدل مناسب باید از متغیرهایی که معنا دار و مرتبط با متغیر پاسخ هستند استفاده شود.
- متغیرهای مستقل، باید نسبت به یکدیگر مستقل باشند. وجود همخطی (Collinearity) بین متغیرهای مستقل، باعث میشود، مدل نامعتبر باشد.
- متغیرهای مستقل دارای رابطه خطی با لگاریتم بختها است.
- برای ایجاد مدل معتبر، حجم نمونه زیاد در رگرسیون لجستیک مورد نیاز است.
با توجه به فرضیات بالا دادههای مربوط به بانک را مورد بررسی قرار میدهیم. اطلاعات جمعآوری شده در فایل اطلاعاتی bank.csv مربوط به نتایج گزارشاتی است که تماسهای تلفنی بخش بازاریابی بانک با مشتریان داشته است. همچنین بعضی از متغیرها از بانک اطلاعات مشتریان استخراج شده است. در فایل اطلاعاتی bank.csv تعداد ۲۰ متغیر مستقل به همراه یک متغیر پاسخ با مقدارهای ۰ و ۱ ثبت شده است. مشخصات این متغیرها در ادامه مورد بررسی قرار گرفتهاند.
متغیرهای ورودی
| نام متغیر | شرح | توضیحات |
| age | سن مشتری | مقدار عددی |
| job | شغل مشتری | متغیر طبقهای با ۱۲ سطح |
| marital | وضعیت تاهل | متغیر طبقهای با ۴ سطح (مجرد- متاهل- طلاق و نامشخص) |
| education | تحصیلات | متغیر طبقهای با ۸ سطح |
| default | مشتری بد حساب | متغیر طبقهای با ۳ سطح (بله - خیر- نامشخص) |
| housing | دارای وام مسکن | متغیر طبقهای با ۳ سطح (بله - خیر- نامشخص) |
| loan | دارای وام بانکی | متغیر طبقهای با ۳ سطح (بله - خیر- نامشخص) |
| contact | نوع تماس با مشتری | متغیر طبقهای با ۲ سطح (تلفن- تلفن همراه) |
| month | ماه آخرین تماس | متغیر طبقهای با ۱۲ سطح (اسامی ماههای سال) |
| day_of_week | روز مربوط به آخرین تماس | متغیر طبقهای براساس ۵ روز کاری |
| duration | طول زمان مکالمه در آخرین تماس | عددی (اگر مقدار این متغیر برابر با ۰ باشد، مشخص است که مقدار y نیز ۰ است. در انتهای این مکالمه نیز مقدار y مشخص میشود که برابر با ۰ یا ۱ است. |
| campaign | تعداد تماسها با مشتری در این طرح | عددی (شامل آخرین مکالمه) |
| pdays | فاصله روزها بین تماس مربوط به دو طرح با مشتری | عددی (مقدار ۹۹۹ بیانگر عدم شرکت در طرح قبلی است) |
| previous | تعداد تماسهای طرح قبلی مشتری | عددی |
| poutcome | نتیجه طرخ قبلی برای مشتری | طبقهای با ۳ سطح (موفق- شکست- ناموجود) |
| emp.var.rate | نرخ تغییرات استخدامی | عددی |
| con.price.idx | شاخص ارزش مصرف | عددی |
| euribor3m | نرخ یورو در داخل بانک در دوره سه ماهه | عددی |
| nr.employed | تعداد کارکنان | عددی |
متغیر پاسخ نیز که با y نشان داده شده است، بیانگر اقدام مشتری در افتتاح حساب سپرده طولانی مدت، y=1 یا عدم تمایل به بازگشایی چنین حسابی، y=0 است. به نظر میرسد که سطحهای متغیر تحصیلات زیاد است، به منظور ایجاد مدل مناسب، بهتر است که این تعداد را کاهش دهیم. در زیر این سطوح دیده میشود.

با ادغام سطوح basic.4y, basic9y و basic6y و تبدیل آنها به سطح basic از تعداد سطوح متغیر تحصیل میکاهیم. کد زیر به این منظور نوشته شده است.
بعد از اجرای این دستورات متغیر تحصیلات (education) به صورت زیر در خواهد آمد.

حال به بررسی خصوصیات و ویژگیهای دادهها و متغیرهای مستقل و وابسته میپردازیم.
بررسی کاوشگرانه در دادهها
دستورات و توابع زیر به منظور ترسیم نمودار برای مقایسه تعداد مشتریانی که به طرح پاسخ مثبت (حساب سپرده طولانی مدت افتتاح کردهاند) و منفی دادهاند، اجرا شدهاند.
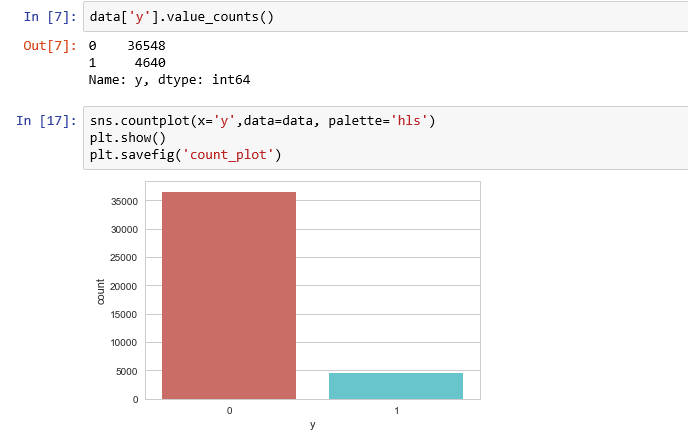
همانطور که مشخص است به نسبت کل مشتریان، تعداد کمی در طرح شرکت کردهاند. این نسبت برای کسانی که در طرح شرکت کردهاند برابر با ۱۱.۲۶۵ درصد و برای کسانی که در طرح شرکت نکردهاند، برابر با ۸۸.۷۳۵ درصد است. کد زیر به منظور محاسبه این درصدها نوشته شده است.
مشخص است که گروهها برحسب مقدار متغیر y متوازن نیستند. نسبت بخت در این حالت تقریبا برابر با 89 به ۱۱ است. نسبت بخت در این حالت از تقسیم تعداد مشتریان با y=0 به مشتریان با پاسخ y=1 بدست میآید. قبل از اینکه گروهها را متوازن کنیم اجازه دهید به دادهها با دقت بیشتری نگاه کنیم. تصویر زیر به بررسی و مقایسه میانگین متغیرهای عددی برای دو گروه y=0 و y=1 پرداخته است.

نتایج مقایسه میانگین دو گروه
با توجه به تغییراتی که میانگین متغیرها در بین این دو گروه دارد، نتایج زیر حاصل میشود.
- میانگین سن مشتریانی که حساب سپرده بلند مدت افتتاح کردهاند بیشتر از بقیه است. (تقریبا یک سال)
- متوسط طول زمان مکالمه برای کسانی که در طرح شرکت کردهاند بیشتر از کسانی است که انصراف دادهاند. البته این موضوع طبیعی است. زیرا کسانی که تمایل به افتتاح حساب دارند باید با کارمند بانک مشاوره بیشتری داشته باشند در نتیجه زمان مکالمه بیشتری نیز مورد احتیاج است.
- با کمال تعجب دیده میشود که متوسط تعداد تماسها برای کسانی که در طرح حساب سپرده بلند مدت شرکت کردهاند، کمتر از افرادی است که تمایل به طرح نداشتهاند. یعنی کسانی که دچار تعلل در تصمیم گیری هستند در نهایت نیز حساب سپرده بلند مدت افتتاح نمیکنند.
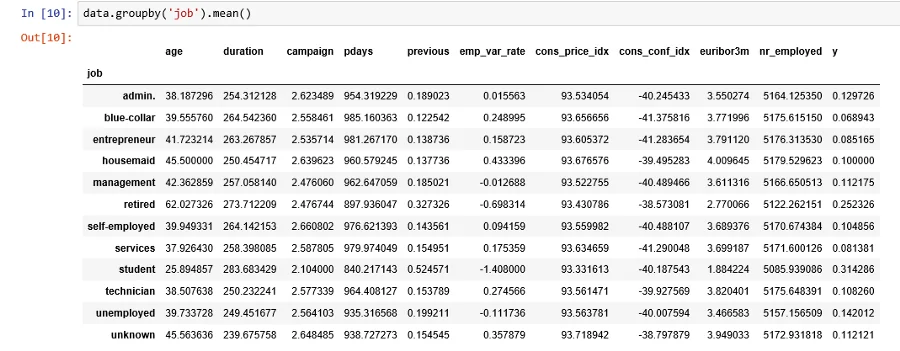
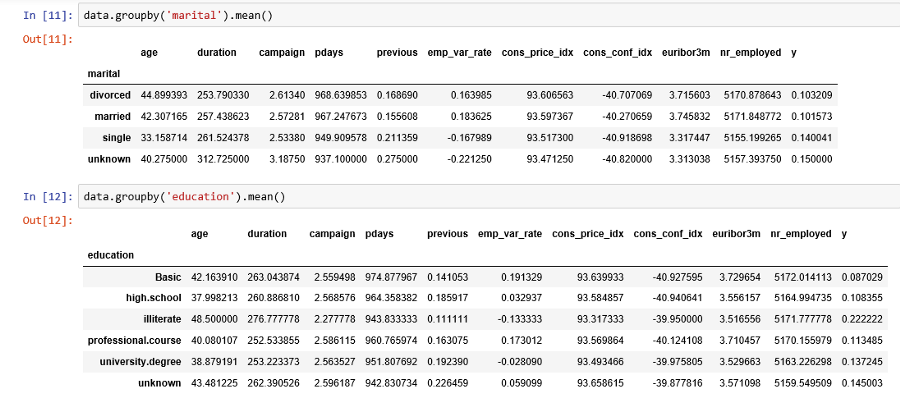
میانگین این متغیرها را نیز میتوان برای گروههایی که توسط متغیرهای طبقهای دیگر ایجاد میشوند، محاسبه کرد و نتایج جالبی گرفت.
تصویر سازی دادهها
با توجه به نقشی که شغل مشتری در انتخاب طرح حساب سپرده دارد، نمودار زیر ترسیم شده است. کد زیر به منظور تهیه این نمودار به کار رفته است.
نتیجه به صورت نمودار زیر خواهد بود.
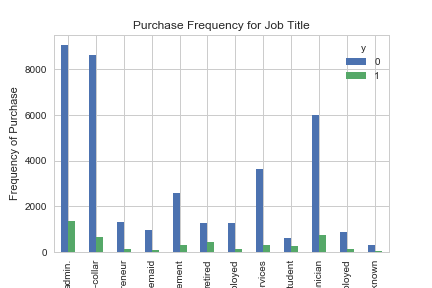
محور افقی نوع فعالیت مشتری (شغل) را نشان میدهد. محور عمودی نیز فراوانی را برای هر شغل بیان میکند. ستونهای آبی رنگ مربوط به مشتریانی است که در طرح شرکت نکردهاند و رنگ سبز مربوط به افرادی است که به افتتاح حساب سپرده بلند مدت اقدام کردهاند. بنابراین به نظر میرسد که نوع شغل افراد در انتخاب طرح موثر است. در ادامه به بررسی نقش متغیرهای طبقهای دیگر در شرکت مشتریان در طرح میپردازیم.
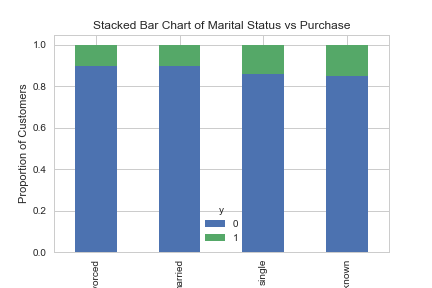
متغیر وضعیت تاهل
با توجه به نمودار ترسیم شده توسط کد بالا، مشخص است که وضعیت تاهل تاثیری برای شرکت در طرح در بین مشتریان ندارد. زیرا درصد کسانی که در طرح شرکت کردهاند با توجه به وضعیت تاهل تغییر چندانی ندارد.
حال به بررسی وضعیت تحصیلات میپردازیم. کد زیر به این منظور تهیه شده است.
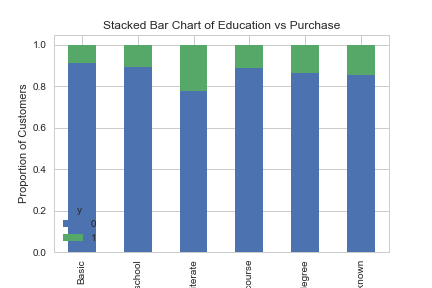
با توجه به تغییر محسوس در سطح تحصیلات برای دو گروه y=0 و y=1 به نظر میرسد که این متغیر میتواند به عنوان یک عامل در رگرسیون لجستیک در مدل به کار رود.
همین کار را برای دو متغیر day_of_week و month نیز انجام میدهیم. کدها و نمودارها به ترتیب به صورت زیر نوشته شدهاند.
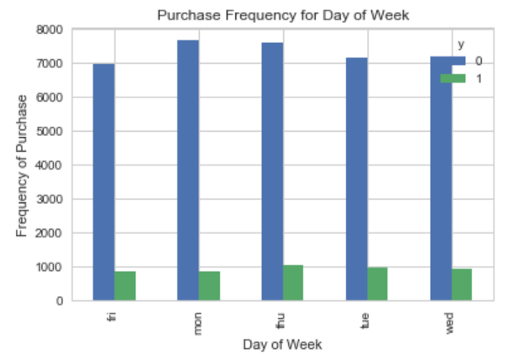
این نمودار به وضوح نشان میدهد که تغییر در روز تماس در هفته، تاثیری در نظر مشتری ندارد.
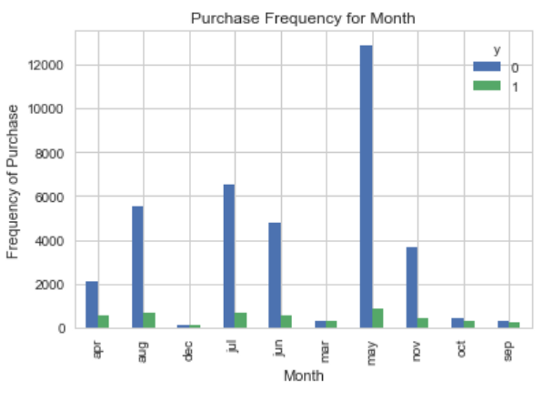
کاملا مشخص است که در ماههای مختلف، میزان مشارکت در طرح تغییر پیدا میکند. بنابراین متغیر Month نیز به عنوان متغیر موثر در تعیین شرکت مشتری در طرح در مدل به کار گرفته خواهد شد. برای مثال در ماههای «دسامبر» (Dec) و «مارچ» (Mar) تقریبا درصد این دو دسته برابر است. همچنین کد زیر به درک رابطه بین متغیر poutcome و متغیر وابسته کمک میکند. با توجه به سطوح متغیر مربوط به نتیجه شرکت مشتری در طرح قبلی، میتوان وضعیت او را در طرح جدید مورد بررسی قرار داد.
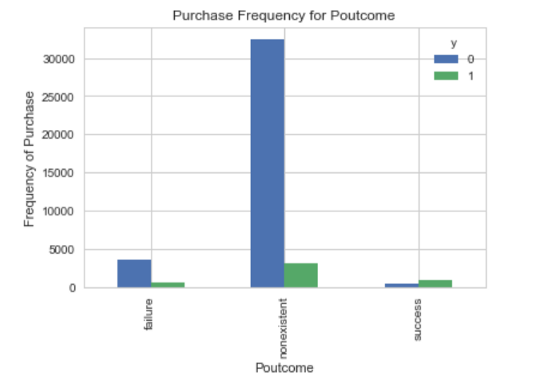
این نمودار نشان میدهد که اکثر کسانی که در طرح قبلی شرکت کردهاند در طرح جدید نیز مشارکت داشتهاند. در ادامه نیز با استفاده از کد زیر و رسم یک هیستوگرام، به بررسی سن مشتریان بانک پرداختهایم.
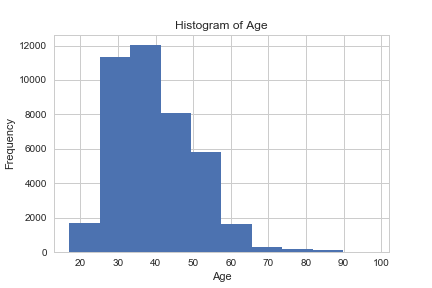
با بررسی این نمودار متوجه میشویم که بیشتر مشتریان بانک در رده سنی ۳۰ تا ۴۰ سال هستند. پس به نظر میرسد که سن نیز میتواند در پیشبینی متغیر پاسخ اهمیت داشته باشد.
ایجاد متغیرها مجازی
اگر در مدل رگرسیونی از متغیرهای طبقهای با بیش از دو سطح یا مقدار، استفاده میکنید، باید هر یک از آنها را به چندین متغیر مجازی با مقدارهای ۰ و ۱ تبدیل کنید.
کد زیر به این منظور نوشته شده است.
به این ترتیب دادههای نهایی و متغیرهایی که در مدل به کار خواهند رفت به صورت زیر خواهند بود.
خروجی این دستور به صورت زیر است.

بیش-نمونهگیری با استفاده از SMOTE
با توجه به اینکه تعداد اعضای دو گروه از مشاهدات با مقدارهای y=1 و y=0 یکسان نیستند، استنباط براساس آنها به راحتی امکان پذیر نیست. به این منظور با استفاده از بیش-نمونهگیری (Over-Sampling) و الگوریتم SMOTE نمونهگیری را انجام میدهیم. الگوریتم SMOTE به ایجاد توازن در نمونهها کمک میکند. الگوریتم SMOTE به صورت زیر عمل میکند.
- با ایجاد نمونههای مصنوعی از گروه اقلیت، حجم این گروه از جامعه را افزایش میدهد. در نتیجه تکرار نمونههای اولیه صورت نخواهد گرفت.
- براساس روش k-NN یا k نزدیکترین همسایه دادههای مشابه و تصادفی تولید میشود.
کدهای زیر به منظور اجرای این الگوریتم روی دادههای بانکی ایجاد شدهاند. این کار احتیاج به کتابخانه imblearn.over_sampling و تابع SMOTE دارد.
خروجی این دستورات ایجاد نمونههای متوازن شده در هر دو گروه است.

همانطور که دیده میشود، دادههای بیش-نمونهگیری فقط روی دادههای آموزشی صورت گرفته است و دادههای آزمایشی روی ایجاد این نمونه نقشی ندارند. به این ترتیب دادههای آزمایشی بر روی مدل تاثیری نخواهند گذاشت.
حذف ویژگیها بر اساس روش برگشتی (Recursive Feature Elimination)
حذف ویژگیهای با روش REF یا (Recursive Feature Elimination) به این شکل صورت میگیرد که براساس اضافه و کم کردن هر یک از ویژگیها، مدل ارزیابی شده و بهترین ویژگیها برای ایجاد مدل انتخاب میشود. به این ترتیب مدل با کمترین تعداد متغیر و بهترین کارایی بدست خواهد آمد. کدهای زیر به این منظور تهیه شدهاند.
این دستورات برای متغیرهای موجود با مشخص کردن False یا True لزوم وجود در مدل را نشان میدهد.

بنابراین ویژگیهای زیر برای ایجاد مدل مناسب تشخیص داده شدهاند. البته ضرورت وجود بعضی از این ویژگیها توسط نمودارهای قبلی مورد بررسی قرار گرفته بود.
“euribor3m”, “job_blue-collar”, “job_housemaid”, “marital_unknown”, “education_illiterate”, “default_no”, “default_unknown”, “contact_cellular”, “contact_telephone”, “month_apr”, “month_aug”, “month_dec”, “month_jul”, “month_jun”, “month_mar”, “month_may”, “month_nov”, “month_oct”, “poutcome_failure”, “poutcome_success”.
با استفاده از کدهای زیر این متغیرها انتخاب خواهند شد.
ایجاد مدل رگرسیون لجستیک
برای ایجاد مدل رگرسیون لجستیک از دستورات زیر در پایتون استفاده میکنیم. به این ترتیب وضعیت مشاهدات و احتمال تعلق به هر یک از گروهها مشخص میشود.
خروجی به صورت زیر دیده خواهد شد. مشخص است که مطابق با رگرسیون خطی برای هر یک از متغیرها در ستون Coef ضریب متغیر مشخص شده است. معیارهای ارزیابی مدل بوسیله پارامترهای AIC و BIC نشان داده شدهاند.
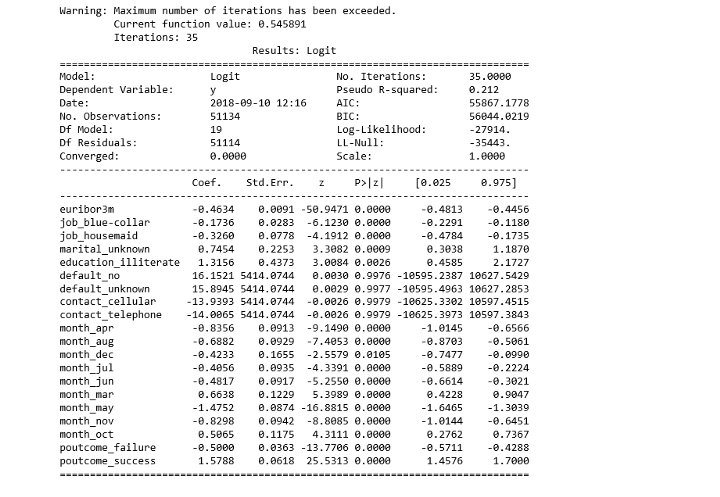
همچنین در ستون مشاهده میشود که مقدار احتمال یا p-value برای بیشتر متغیرها از 0.05 کمتر است به جز چهار متغیر default_no, default_unknown, contact_cellular و contact_telephone که در ادامه آنها را از مدل خارج میکنیم.
خروجی در این حالت به صورت زیر دیده خواهد شد.
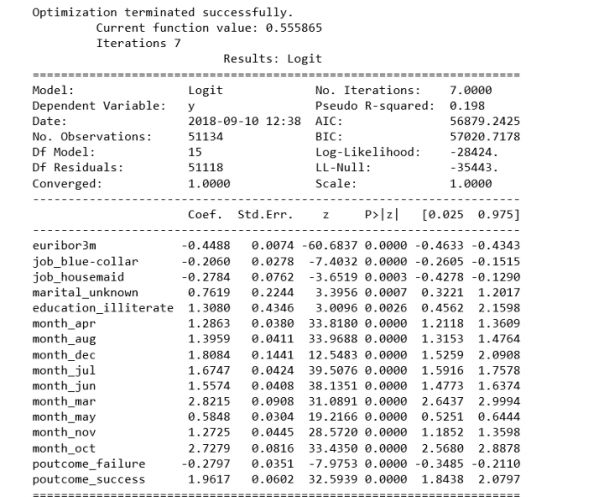
به این ترتیب با ۷ بار تکرار مدل به مقدار بهینه رسیده و برآورد ضرایب مدل بدست آمده است.
برازش دادهها براساس مدل رگرسیون لجستیک
حال به منظور بررسی مدل و اجرای نتایج حاصل از مدل روی دادههای آزمایشی از دستورات زیر استفاده میکنیم.
مشخص است که در کد نوشته شده ۳۰درصد دادهها به عنوان دادههای آزمایشی در نظر گرفته شده است.
دقت مدل حاصل را بوسیله کدهای زیر اندازهگیری میکنیم. نتیجه محاسبه برابر با 0.74 یا 74 درصد است. به این معنی که برای دادههای آزمایشی، مدل ۷۴٪ مواقع نتیجه درست را برای متغیر پاسخ y حدس زده است.
ماتریس درهم ریختگی (Confusion Matrix)
به منظور اندازهگیری کارایی مدل از معیارهای دیگری مانند «دقت» (Precision)، «صحت» (Recall) ، «اندازه F» و همچنین «تکیهگاه» (Support) نیز میتوان استفاده کرد. برای به کارگیری هر یک از این معیارهای بهتر است ابتدا با مفاهیم اولیه مرتبط با شیوه محاسبه آنها آشنا شویم.
- TP : نشانگر تعداد حالتهایی است که مقدار پیشبینی شده با مقدار واقعی برای متغیر پاسخ برابر با ۱ هستند.
- FP: بیانگر تعداد حالتهایی است که مقدار پیشبینی شده برای متغیر پاسخ، با مقدار واقعی برابر و با ۰ برابر هستند.
- FN: بیانگر تعداد حالتهایی است که مقدار پیشبینی برابر با 0 ولی مقدار واقعی برای متغیر پاسخ برابر با 1 است.
حال به معرفی شاخهای ارزیابی براساس این مشخصات میپردازیم.
معیار دقت: نسبت مقدار TP به حاصل جمع TP و FP، دقت را محاسبه میکند. به این ترتیب این معیار نشان میدهد با چه درصدی مدل به مشاهدهای که مقدار ۰ دارد برچسب ۱ نداده است.
معیار صحت: این معیار نشان میدهد که با چه درصدی، مشاهدات با مقدار واقعی ۱ برای متغیر پاسخ توسط مدل نیز مقدار ۱ را گرفتهاند.
اندازه F: از آنجایی که هر دو معیار دقت و صحت به صورت درصدی هستند. برای محاسبه میانگین آنها باید از میانگین همساز (Harmonic Mean) استفاده کرد. میانگین همساز وزنی با وزن بین این دو معیار به مقدار F یا اندازه F () مشهور است. در این حالت به وزن معیار صحت گفته میشود. اگر مقدار باشد، وزن هر دو معیار صحت و دقت در محاسبه اندازه F یکسان خواهد بود.
تکیهگاه: تعداد مشاهده مقدار ۱ و ۰ در مشاهدات، تکیهگاه را مشخص میکند. کد زیر به منظور استخراج این معیارها استفاده شده و خروجی به صورت زیر حاصل میشود.
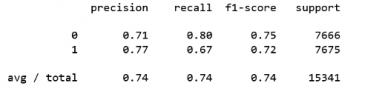
براساس سطر آخر این جدول مشخص است که 74٪ پیشبینیها توسط مدل درست بوده است.
منحنی ROC
روش دیگر برای نشان دادن حساسیت مدل استفاده از نمودار ROC یا نمودار Receiver Operating Characteristic است. در نمودار رسم شده، خطی که به صورت مقطع و قرمز رنگ ظاهر شده دسته بندی تصادفی مشتریان را نشان میدهد. یک مدل رگرسیون لجستیک باید نرخ TP بیشتری نسبت به مدل تصادفی داشته باشد. پس خط آبی رنگ باید دور از خط قرمز رنگ قرار گیرد. به این ترتیب با توجه به نمودار رسم شده صحت مدل رگرسیون لجستیک ایجاد شده مورد تایید قرار میگیرد.
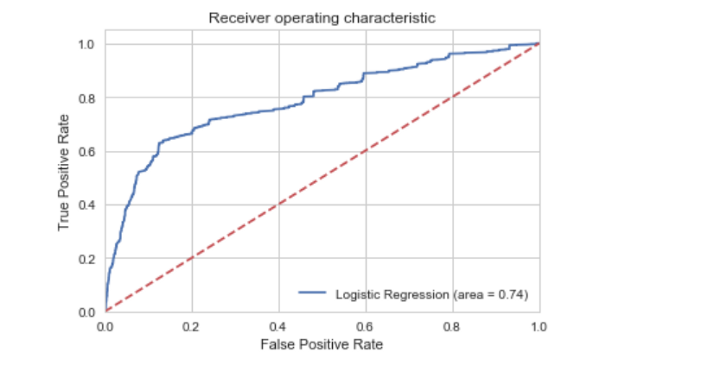
این نمودار توسط دستورات زیر ترسیم شده است.
تمام کدهای مربوط به این متن در (+) در قالب Jupyter notebook قابل دسترس است.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های SPSS
- مجموعه آموزش های داده کاوی یا Data Mining در متلب
- آموزش همبستگی و رگرسیون خطی در SPSS
- مجموعه آموزشهای یادگیری ماشین و بازشناسی الگو
- مجموعه آموزشهای نرمافزارهای آماری
- ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها
- مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری
^^












سلام
خب 74 درصد عدد پایینی هست، برای بهبودش باید چه کنیم؟
از مدل دیگه ای استفاده کنیم یا با تغییر بعضی پارامتر ها میشه همین مدل رو بهبود داد؟