ممان اینرسی استوانه تو پر،‌ توخالی و میله – به زبان ساده

لختی دورانی یا ممان اینرسی استوانه، کمیتی است که توزیع جرم اجسام استوانه‌ای شکل را حول یک محور مشخص نمایش می‌دهد. اگر استوانه‌ای را حول یک محور مشخص دوران دهیم، ذرات آن در برابر شتاب ناشی از دوران (شتاب زاویه‌ای) مقاومت می‌کنند. مقاومت استوانه در برابر شتاب زاویه‌ای، توسط ممان اینرسی استوانه نشان داده می‌شود. این کمیت، تابعی از جرم ذرات استوانه و فاصله آن‌ها تا محور دوران است. به این ترتیب، محاسبه ممان اینرسی استوانه با ضرب جرم ذرات تشکیل دهنده آن در مربع فاصله هر ذره تا محور دوران و جمع این حاصل‌ضرب‌ها انجام می‌گیرد. استوانه‌های توپر و توخالی، از شکل‌های پرکاربرد در حوزه‌های مهندسی و تولید قطعات هستند که از ممان اینرسی بالا بهره می‌برند. از این‌رو، بسیاری المان‌های تحت پیچش، به این شکل ساخته می‌شوند. در این مقاله، به معرفی فرمول ممان اینرسی استوانه توپر، توخالی و یکی از شکل‌های مرتبط با این استوانه، یعنی میله می‌پردازیم.

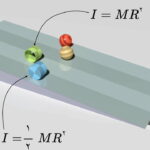
تعریف ممان اینرسی

«ممان اینرسی» (Moment of Inertia)، معیاری برای مقایسه مقاومت شکل‌های مختلف در برابر شتاب زاویه‌ای است. این کمیت، نحوه توزیع ذرات جسم حول یک محور مشخص را نمایش می‌دهد. به محور مذکور، محور دوران می‌گویند. ممان اینرسی با عناوین دیگری نظیر «ممان اینرسی جرمی» (Mass Moment of Inertia)، «جرم زاویه‌ای» (Angular Mass)، «گشتاور دوم جرم» (Second Moment of Mass) یا به طور دقیق‌تر، «لختی دورانی» (Rotational inertia) نیز شناخته می‌شود.

تصویر زیر، مفهوم ممان اینرسی در اجسام مختلف را نمایش می‌دهد. هرچه ممان اینرسی جسم کمتر باشد، شتاب‌زاویه‌ای آن بیشتر خواهد بود. بنابراین، جسم دارای ممان اینرسی کمتر، زودتر از دیگر اجسام به انتهای مسیر می‌رسد. همان‌طور که مشاهده می‌کنید، ممان اینرسی استوانه توخالی، از ممان اینرسی کره توخالی، استوانه توپر و کره توپر بیشتر است.

با توجه به تعریف ممان اینرسی، این کمیت از ضرب جرم هر یک از ذرات تشکیل‌دهنده جسم در فاصله آن ذرات تا محور دوران و جمع حاصل‌ضرب‌ها به دست می‌آید. به عبارت دیگر، اگر یک جسم، دارای n ذره، ممان اینرسی جسم برابر خواهد بود با:

$$
I = \sum _ { i = ۱ } ^ { i = n } m _ i r _ i ^ ۲
$$

• I: ممان اینرسی جسم
• m_i: جرم ذره i ام
• r_i: فاصله ذره i ام تا محور دوران
• n: تعداد ذرات جسم

این رابطه، فرمول گسسته ممان اینرسی است. فرمول پیوسته ممان اینرسی یا همان فرم دیفرانسیلی رابطه بالا، به صورت زیر نوشته می‌شود:

$$
I = \int r ^ ۲ d m
$$

همان‌طور که مشاهده می‌کنید، ممان اینرسی با مربع فاصله ذرات تا محور دوران نسبت مستقیم دارد. ممان اینرسی اغلب شکل‌های شناخته شده، معمولا حول محور گذرنده از مرکز جرم آن‌ها به دست می‌آید. با فاصله گرفتن از مرکز جرم، به مقدار ممان اینرسی افزوده می‌شود. در ادامه، تمام این نکات را برای یکی از شکل‌های معروف هندسی، یعنی استوانه، مورد بررسی قرار می‌دهیم.

ممان اینرسی استوانه چگونه بدست می آید ؟

«استوانه» (Cylinder)، یکی از شکل‌های معروف هندسی است که از گسترش دایره در بعد سوم ایجاد می‌شود.

تصویر زیر، شکل استوانه را نمایش می‌دهد. قاعده دایره‌ای و سطح منحنی، اجزای اصلی تشکیل‌دهنده استوانه هستند.

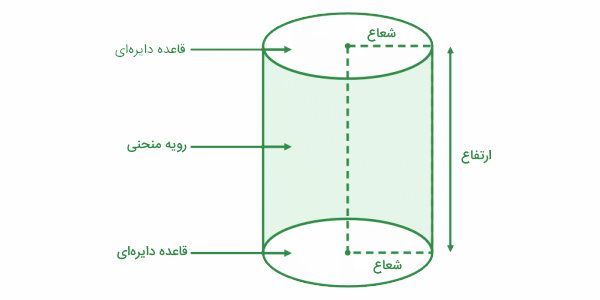
مرکز جرم استوانه، در میانه محور عبوری از مراکز قاعده‌ها قرار دارد. این محور، به عنوان محور مرکزی استوانه در نظر گرفته می‌شود و معمولا به منظور محاسبه ممان اینرسی مورد استفاده قرار می‌گیرد.

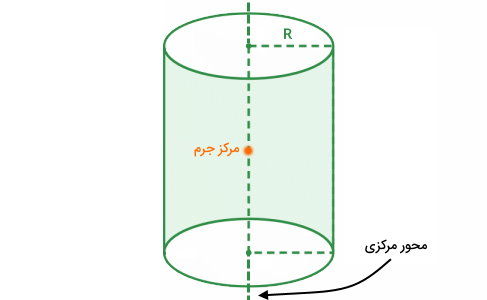
فرمول ممان اینرسی استوانه توپر به صورت زیر نوشته می‌شود:

$$ I = \frac { ۱ } { ۲ } M R ^ ۲ $$

• I: ممان اینرسی استوانه توپر
• M: جرم استوانه
• R: شعاع قاعده استوانه (شعاع دایره)

فرمول بالا، لختی دورانی استوانه حول محور مرکزی را نمایش می‌دهد. اگر محور دوران، موازی با محور مرکزی و بر روی سطح خارجی استوانه قرار داشته باشد، فرمول ممان اینرسی به شکل زیر درمی‌آید:

$$
I = \frac { ۳ } { ۲ } M R ^ ۲
$$

در اغلب موارد، محور گذرنده از مرکز قاعده‌های استوانه و مرکز جرم آن را منطبق بر محور z در دستگاه مختصات سه‌بعدی در نظر می‌گیرند. بنابراین، منظور از $$ I _ z $$، همان ممان اینرسی حول محور مرکزی است.

علامت ممان اینرسی استوانه چیست ؟

ممان اینرسی استوانه، با حرف انگلیسی I نمایش داده می‌شود. این حرف، ابتدای عبارت «Inertia»، به معنی اینرسی یا لختی است. در اکثر موارد، منظور از I، ممان اینرسی گذرنده از مرکز جرم شکل است. البته امکان استفاده از اندیس «cm» یا «CM» برای نشان دادن این ممان اینرسی (_Icm یا I_CM) نیز وجود دارد. این اندیس‌ها، ابتدای کلمات موجود در «Center Mass» به معنای «مرکز جرم» را نمایش می‌دهند. در برخی از موارد، ممان اینرسی حول محورهای معلوم را با اندیس این محورها مشخص می‌کنند. به عنوان مثال، ممان اینرسی حول محور z، با I_z نمایش داده می‌شود.

یکای ممان اینرسی استوانه چیست ؟

ممان اینرسی استوانه، از ضرب کمیت جرم در مربع کمیت طول به دست می‌آید. بنابراین، یکای آن در سیستم‌های مختلف، به صورت جرم در طول مربع بیان می‌شود. به عنوان مثال، یکای ممان اینرسی در سیستم SI، کیلوگرم در متر مربع (kg.m^۲) است.

کابرد ممان اینرسی استوانه چیست ؟

استوانه، یکی از شکل‌های پرکاربرد در علوم مختلف است. بسیاری از وسیله‌های مورد استفاده ما، به شکل استوانه‌ای بوده یا دارای قطعات استوانه‌ای شکل هستند.

با این وجود، ممان اینرسی استوانه، اغلب در تحلیل خمش و پیچش اجسام تحت تنش خمشی (نظیر تیرها و شفت‌های دارای مقطع دایره‌ای) کاربرد دارد. صنایع خودروسازی و کشتی‌سازی، از مهم‌ترین حوزه‌های به‌کارگیری مفهوم ممان اینرسی استوانه هستند؛ چراکه اغلب المان‌های تحت پیچش، به شکل استوانه ساخته می‌شوند.

مثال ۱: محاسبه ممان اینرسی استوانه حول محور z

یک استوانه توپر به جرم ۱۲۰۰ کیلوگرم، شعاع قاعده ۲ متر و ارتفاع ۷ متر را در نظر بگیرید.

• ممان اینرسی این استوانه توپر حول محور z چقدر است؟
• اگر ارتفاع استوانه را دو برابر کنیم، ممان اینرسی آن چه تغییری می‌کند؟

محور z، محوری است که از مرکز قاعده‌های استوانه و مرکز جرم آن عبور می‌کند. لختی دورانی استوانه حول این محور، توسط رابطه زیر به دست می‌آید:

$$ I = \frac { ۱ } { ۲ } M R ^ ۲ $$

• I: ممان اینرسی استوانه توپر
• M: جرم استوانه برابر با ۱۲۰۰ کیلوگرم
• R: شعاع قاعده استوانه برابر با ۲ متر

مقادیر پارامترهای معلوم را درون فرمول قرار می‌دهیم:

$$ I _ z = \frac { ۱ } { ۲ } \times ۱۲۰۰ \times ۲ ^ ۲ $$

$$ I _ z = \frac { ۱ } { ۲ } \times ۱۲۰۰ \times ۴ $$

$$ I _ z = ۱۲۰۰ \times ۲ $$

$$ I _ z = ۲۴۰۰ $$

در نتیجه، ممان اینرسی استوانه توپر حول محور z برابر با ۲۴۰۰ کیلوگرم در متر مربع است. اگر ارتفاع استوانه را دو برابر کنیم، هیچ تغییری در ممان اینرسی رخ نمی‌دهد؛ چراکه با توجه به فرمول، ارتفاع در تعیین این کمیت نقشی ندارد.

اثبات فرمول ممان اینرسی استوانه توپر

به منظور اثبات فرمول ممان اینرسی استوانه توپر، شکل زیر را در نظر بگیرید. این شکل، استوانه‌ای به شعاع R و ارتفاع L را نمایش می‌دهد. محور z، محور مرکزی استوانه است.

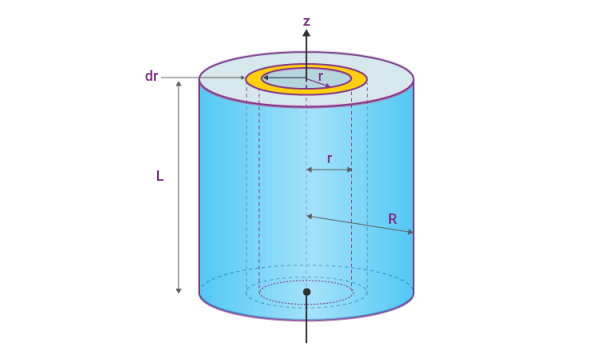
ابتدا استوانه توپر را به صورت مجموعه‌ای از استوانه‌های نازک در نظر می‌گیریم. هر استوانه، دارای ضخامت dr، ارتفاع L و شعاع r است.

با جمع ممان‌های اینرسی این استوانه‌های جدار نازک، به ممان اینرسی استوانه توپر می‌رسیم.

مرحله اول: نوشتن فرمول کلی ممان اینرسی

فرمول کلی ممان اینرسی به صورت زیر نوشته می‌شود:

$$
I = \int r ^ ۲ d m
$$

از هر دو طرف انتگرال بالا مشتق می‌گیریم:

$$ d I = r ^ ۲ d m $$

این رابطه، ممان اینرسی یک المان جزئی را نمایش می‌دهد. در اجسام استوانه‌ای، dI، بیانگر ممان اینرسی استوانه‌های نازک است. در این رابطه داریم:

• dI: ممان اینرسی المان جزئی استوانه
• r: شعاع داخلی مقطع المان
• dm: جرم هر یک از المان‌های استوانه

مرحله دوم: بازنویسی پارامترها بر حسب r

چگالی هر یک از المان‌های جزئی استوانه برابر است با:

$$ \rho = \frac { d m } { d V } $$

• ρ: چگالی استوانه
• dm: جرم المان جزئی
• dV: حجم المان جزئی

حجم یک المان استوانه‌ای، از ضرب مساحت مقطع در ارتفاع آن به دست می‌آید:

$$ d V = d A L $$

• dV: حجم المان جزئی
• dA: مساحت مقطع المان جزئی
• L: ارتفاع المان جزئی

ضخامت المان استوانه‌ای، برابر با dr است. با توجه به این موضوع، شعاع داخلی حلقه برابر با r و شعاع خارجی آن برابر با r+dr می‌شود. به این ترتیب، مساحت المان جزئی استوانه از رابطه زیر به دست می‌آید:

$$ d A = \pi ( r + d r ) ^ ۲ - \pi r ^ ۲ $$

$$
\begin {array} { l } d A = \pi ( r ^ { ۲ } + ۲ r d r + ( d r ) ^ { ۲ }) – \pi r ^ { ۲ } \end {array}
$$

dr^۲، مقدار بسیار کوچکی است. بنابراین، این عبارت را برابر با صفر قرار می‌دهیم. بنابراین، داریم:

$$
\begin {array} { l } d A = \pi r ^ { ۲ } + ۲ \pi r d r + \pi ( d r ) ^ { ۲ } – \pi r ^ { ۲ } \end {array}
$$

$$
\begin {array} { l } d A = ۲ \pi r d r + ۰ \end {array}
$$

$$
\begin {array} { l } d A = ۲ \pi r d r \end {array}
$$

مرحله سوم: جایگذاری پارامترها در فرمول کلی

در مرحله قبلی، رابطه dA را بر حسب r بازنویسی کردیم. معادل dA را درون رابطه dV قرار می‌دهیم:

$$
\begin {array} { l } d V = d A L = ۲ \pi r d r L \end {array}
$$

اکنون، از رابطه بالا برای بازنویسی dm بر حسب r استفاده می‌کنیم:

$$
d m = \rho d V = \rho (۲ \pi r dr L )
$$

با قرار عبارت‌های بالا در فرمول کلی ممان اینرسی المان جزئی استوانه، خواهیم داشت:

$$
\begin {array} { l } d I = r ^ { ۲ }( ۲\pi r d r ) L\rho \end {array}
$$

از دو طرف معادله انتگرال می‌گیریم:

$$
\int \begin {array} { l } d I = \int r ^ { ۲ }( ۲\pi r d r ) L\rho \end {array}
$$

$$
I = \int r ^ { ۲ }( ۲\pi r d r ) L\rho
$$

با گرفتن انتگرال در بازه ۰ تا R، ممان اینرسی استوانه به دست می‌آید:

$$
I = \int _ { ۰ } ^ { R } r ^ { ۲ }( ۲\pi r d r ) L\rho
$$

$$
I = ۲ \pi L \rho \int _ { ۰ } ^ { R } r ^ { ۳ } d r
$$

$$
I = ۲ \pi L \rho [ \frac { r ^ ۴ } { ۴ } ] _ { ۰ } ^ { R }
$$

$$
I = ۲ \pi L \rho [ \frac { R ^ ۴ } { ۴ } - \frac { ۰ ^ ۴ } { ۴ } ]
$$

$$
I = ۲ \pi L \rho [ \frac { R ^ ۴ } { ۴ } - ۰ ]
$$

$$
I = ۲ \pi L \rho \frac { R ^ ۴ } { ۴ }
$$

$$
I = \pi L \rho \frac { R ^ ۴ } { ۲ }
$$

$$
I = \frac { ۱ } { ۲ } \pi L \rho R ^ ۴
$$

مرحله چهارم: بازنویسی فرمول کلی بر حسب جرم و شعاع

فرمول به دست آمده برای ممان اینرسی استوانه در مرحله قبل، بر حسب ارتفاع، چگالی و شعاع بود. در این مرحله، قصد داریم این فرمول را تا حد ممکن ساده کنیم.

به این منظور، رابطه چگالی استوانه را می‌نویسیم:

$$ \rho = \frac { M } { V } $$

• ρ: چگالی استوانه
• M: جرم استوانه
• V: حجم استوانه

حجم استوانه از رابطه زیر به دست می‌آید:

$$ V = \pi R ^ ۲ L $$

این رابطه را درون رابطه چگالی قرار می‌دهیم:

$$ \rho = \frac { M } { \pi R ^ ۲ L } $$

با قرار دادن فرم بازنویسی شده چگالی در رابطه ممان اینرسی، خواهیم داشت:

$$
I = \frac { ۱ } { ۲ } \pi L \frac { M } { \pi R ^ ۲ L } R ^ ۴
$$

$$
I = \frac { ۱ } { ۲ } \times \frac { \pi R ^ ۴ L M } { \pi R ^ ۲ L }
$$

$$
I = \frac { ۱ } { ۲ } M R ^ ۲
$$

به این ترتیب، فرمول ممان اینرسی استوانه اثبات می‌شود.

قضیه محور های موازی برای ممان اینرسی استوانه توپر

ممان اینرسی شکل‌های هندسی، معمولا حول محور گذرنده از مرکز جرم محاسبه می‌شود. در صورتی که محور دوران مورد نظر، موازی با محور مرکزی باشد، ممان اینرسی از رابطه زیر به دست می‌آید:

$$
I = I _ { c m } + M d ^ ۲
$$

• I: ممان اینرسی حول محور موازی با محور گذرنده از مرکز جرم
• I_cm: ممان اینرسی حول محور گذرنده از مرکز جرم
• M: جرم
• d: فاصله محور دوران با محور گذرنده از مرکز جرم

به این رابطه، «قضیه محورهای موازی» (Parallel Axis Theorem) می‌گویند. شکل زیر را در نظر بگیرید.

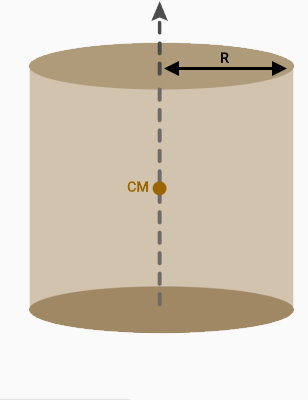
محور عبوری از نقطه CM، محور مرکزی استوانه را نمایش می‌دهد. ممان اینرسی استوانه حول این محور برابر است با:

$$ I _ { c m }= \frac { ۱ } { ۲ } M R ^ ۲ $$

• I_cm: ممان اینرسی حول محور گذرنده از مرکز جرم استوانه
• M: جرم استوانه
• R: شعاع قاعده استوانه

محوری موازی با محور مرکزی و در فاصله R از آن را در نظر بگیرید. این محور، بر روی سطح خارجی استوانه قرار دارد.

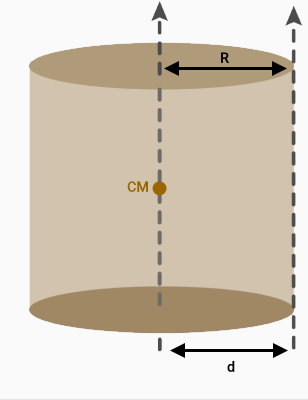
ممان اینرسی استوانه حول محور مذکور،به صورت زیر محاسبه می‌شود:

$$
I = I _ { c m } + M d ^ ۲
$$

$$ I = \frac { ۱ } { ۲ } M R ^ ۲ + M d ^ ۲ $$

به جای d، فاصله دو محور (R) را قرار می‌دهیم:

$$
I = \frac { ۱ } { ۲ } M R ^ ۲ + M R ^ ۲
$$

$$
I = \frac { M R ^ ۲ } { ۲ } + \frac { ۲ M R ^ ۲ } { ۲ }
$$

$$
I = \frac { M R ^ ۲ + ۲ M R ^ ۲ } { ۲ }
$$

$$
I = \frac { ۳ M R ^ ۲ } { ۲ }
$$

$$
I = \frac { ۳ } { ۲ } M R ^ ۲
$$

به این ترتیب، فرمول ممان اینرسی استوانه، حول محور منطبق بر روی ارتفاع در سطح خارجی آن به دست می‌آید. همان‌طور که مشاهده می‌کنید، مقدار این ممان اینرسی، بیشتر از ممان اینرسی حول محور مرکزی است. به طور دقیق، نسبت این دو برابر است با:

$$
\frac { I } { I _ { c m } } = \frac { \frac { ۳ } { ۲ } M R ^ ۲ } { \frac { ۱ } { ۲ } M R ^ ۲ }
$$

$$
\frac { I } { I _ { c m } } = \frac { \frac { ۳ } { ۲ }} { \frac { ۱ } { ۲ } }
$$

$$
\frac { I } { I _ { c m } } = ۳
$$

در نتیجه، تغییر موقعیت محور دوران از موقعیت مرکزی به سطح خارجی استوانه، ممان اینرسی سه برابر می‌شود.

مثال ۲: محاسبه ممان اینرسی استوانه توپر حول محور دلخواه

جرم یک استوانه توپر برابر با ۱۱۵ کیلوگرم و شعاع آن برابر با ۲۰ سانتی‌متر است. لختی دورانی استوانه حول محور موازی با محور z و در فاصله ۰/۳ متری از آن، چند برابر لختی دورانی استوانه حول محور مرکزی است؟

لختی دورانی حول محور موازی با محور مرکزی، از رابطه زیر به دست می‌آید:

$$
I = I _ { c m } + M d ^ ۲
$$

• I: ممان اینرسی حول محور موازی با محور گذرنده از مرکز جرم
• I_cm: ممان اینرسی حول محور گذرنده از مرکز جرم
• M: جرم
• d: فاصله محور دوران با محور گذرنده از مرکز جرم

برای تعیین I، به I_cm نیاز داریم. این پارامتر، همان ممان اینرسی استوانه حول محور z است که به صورت زیر محاسبه می‌شود:

$$ I _ z = \frac { ۱ } { ۲ } M R ^ ۲ $$

• I_z: ممان اینرسی استوانه توپر
• M: جرم استوانه برابر با ۱۱۵ کیلوگرم
• R: شعاع قاعده استوانه برابر با ۰/۲ متر (تبدیل واحد شعاع از سانتی‌متر به متر)

$$ I _ z = \frac { ۱ } { ۲ } \times ۱۱۵ \times ۰/۲ ^ ۲ $$

$$ I _ z = \frac { ۱ } { ۲ } \times ۱۱۵ \times ۰/۰۴ $$

$$ I _ z = ۱۱۵ \times ۰/۰۲ $$

$$ I _ z = ۲/۳ $$

بنابراین، ممان اینرسی حول محور z برابر با ۲/۳ کیلوگرم در متر مربع است. این مقدار را به همراه مقادیر پارامترهای دیگر درون رابطه I قرار می‌دهیم:

$$ I = ۲/۳ + ( ۱۱۵ \times ۰/۲ ^ ۲ ) $$

$$ I = ۲/۳ + ( ۱۱۵ \times ۰/۰۴ ) $$

$$ I = ۲/۳ + ۴/۶ $$

$$ I = ۶/۹ $$

اکنون، I را بر I_z تقسیم می‌کنیم:

$$ \frac { I } { I _ z } = \frac { ۶/۹I } { ۲/۳ } $$

$$ \frac { I } { I _ z } = ۳ $$

در نتیجه، لختی دورانی استوانه حول محور موازی با محور z و در فاصله ۰/۳ متری از آن، سه برابر لختی دورانی استوانه حول محور مرکزی است.

ممان اینرسی استوانه توپر حول محور عمودی

در بخش‌های قبلی، ممان اینرسی استوانه توپر حول محور گذرنده از مرکز جرم (محور عبوری از مرکز قاعده‌ها) را معرفی کردیم. در این بخش، به معرفی فرمول ممان اینرسی استوانه، حول محور عمود بر میانه ارتفاع می‌پردازیم.

این محور، از قطر مرکزی استوانه می‌گذرد. تصویر زیر، موقعیت قرارگیری محور عمود بر ارتفاع استوانه را نمایش می‌دهد.

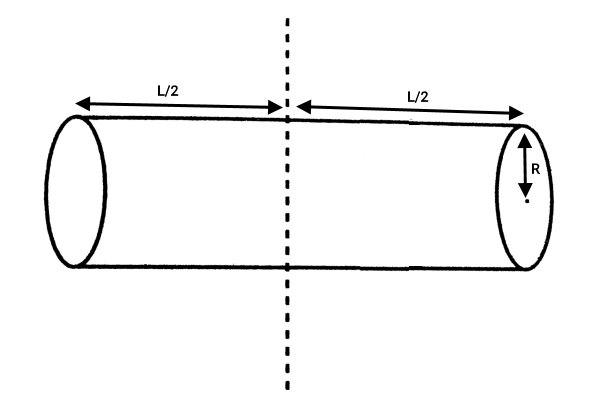
ممان اینرسی استوانه توپر حول محور عمودی گذرنده از قطر مرکزی از رابطه زیر به دست می‌آید:

$$ I = \frac { ۱ } { ۴ } M R ^ ۲ + \frac { ۱ } { ۱۲ } M L ^۲ $$

• I: ممان اینرسی استوانه توپر حول محور عمودی گذرنده از قطر مرکزی
• M: جرم استوانه
• R: شعاع قاعده استوانه
• L: ارتفاع استوانه

ممان اینرسی استوانه توپر حول محورهای عمودی گذرنده از قطرهای انتهایی (محورهای منطبق بر هر قاعده) نیز عبارت است از:

$$ I = \frac { ۱ } { ۴ } M R ^ ۲ + \frac { ۱ } { ۳ } M L ^۲ $$

• I: ممان اینرسی استوانه توپر حول محور عمودی گذرنده از قطر انتهایی

در ادامه، نحوه به دست آوردن این فرمول‌ها را آموزش خواهیم داد.

قضیه محورهای عمودی برای ممان اینرسی استوانه توپر

اگر جسمی، در دو جهت از سه جهت اصلی دستگاه محورهای مختصات سه‌بعدی، دارای تقارن باشد، می‌توان ممان اینرسی آن حول یک محور را بر حسب ممان اینرسی حول دو محور دیگر نوشت. به عنوان مثال، اگر جسمی در راستای محورهای x و y، متقارن باشد، ممان اینرسی آن حول محور z، به صورت زیر نوشته می‌شود:

$$ I _ z = I _ x + I _ y $$

این رابطه، با عنوان «قضیه محورهای عمود» (Perpendicular Axis Theorem) شناخته می‌شود. در ادامه، از این قضیه برای اثبات فرمول ممان اینرسی حول محور عمود بر ارتفاع استوانه استفاده می‌کنیم.

اثبات فرمول ممان اینرسی استوانه حول محور عمودی

استوانه زیر را در نظر بگیرید. ارتفاع این استوانه، در راستای محور z است. قاعده این استوانه نیز در صفحه x-y قرار دارد. نقطه CM، مرکز جرم استوانه را نمایش می‌دهد.

موقعیت این نقطه، بر روی میانه ارتفاع گذرنده از محور تقارن استوانه است.

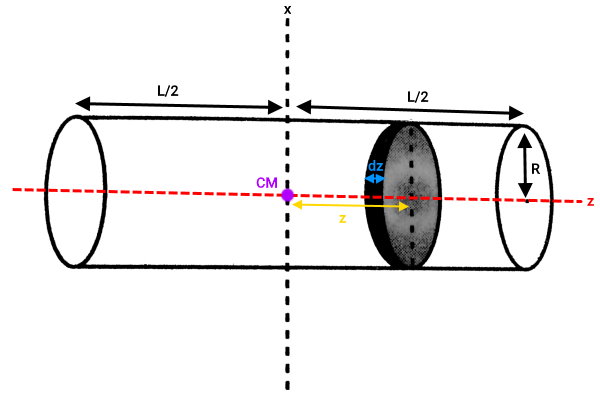
به منظور تعیین ممان اینرسی استوانه حول محور عمودی x، المان کوچکی از استوانه را مطابق با شکل بالا در نظر می‌گیریم. این المان، یک استوانه کوچک با ارتفاع جزئی (dz) است. ممان اینرسی استوانه حول محور x، از جمع ممان‌های اینرسی تمام المان‌های استوانه در بازه $$ - \frac { L } { ۲ } $$ تا $$ \frac { L } { ۲ } $$ به دست می‌آید. بر اساس قضیه محورهای عمودی داریم:

$$ I _ z = I _ x + I _ y $$

این قضیه برای المان جزئی استوانه، به صورت زیر نوشته می‌شود:

$$ d I _ z = d I _ x + d I _ y $$

به دلیل متقارن بودن مقطع استوانه در صفحه x-y (صفحه موازی با قاعده‌ها)، ممان اینرسی حول محورهای x و y، یکسان است. بنابراین، داریم:

$$ d I _ x = d I _ y $$

$$ d I _ z = d I _ x + d I _ x $$

$$ d I _ z = ۲ d I _ x $$

$$ d I _ x = \frac { ۱ } { ۲ } d I _ z $$

ممان اینرسی استوانه حول محور z برابر است با:

$$ I _ z = \frac { ۱ } { ۲ } M R ^ ۲ $$

فرم دیفرانسیلی این فرمول به صورت زیر نوشته می‌شود:

$$ d I _ z = \frac { ۱ } { ۲ } d m R ^ ۲ $$

به این ترتیب، dx برابر خواهد بود با:

$$ d I _ x = \frac { ۱ } { ۲ } d I _ z $$

$$ d I _ x = \frac { ۱ } { ۲ } \times \frac { ۱ } { ۲ } d m R ^ ۲ $$

$$
d I _ x = \frac { ۱ } { ۴ } d m R ^ ۲
$$

این رابطه، ممان اینرسی جزئی یکی از المان‌های عمودی استوانه (ممان اینرسی دیسک) حول محور گذرنده از مرکز آن را نمایش می‌دهد. برای به دست آوردن ممان اینرسی کل استوانه، باید ممان‌های اینرسی تمام المان‌ها را در راستای محور z با یکدیگر جمع کنیم. از آنجایی که این المان‌ها بر روی محور z قرار دارند، dm را بر حسب dz بازنویسی می‌کنیم. چگالی استوانه از رابطه زیر به دست می‌آید:

$$ \rho = \frac { M } { V } $$

توزیع جرم در حجم استوانه، یکنواخت است. بنابراین، چگالی یک المان از آن نیز به صورت زیر تعریف می‌شود:

$$ \rho = \frac { d m } { d V } $$

به این ترتیب، dm برابر است با:

$$ d m = \rho d V $$

dV، حجم یک المان جزئی از استوانه را نمایش می‌دهد. این حجم، از رابطه زیر به دست می‌آید:

$$ d V = A d z $$

A، مساحت سطح مقطع المان (مساحت دایره) و dz، ضخامت المان است. در رابطه dm، به جای ρ و dV، معادل آن‌ها را قرار می‌دهیم:

$$ d m = \frac { M } { V } \times A d z $$

حجم استوانه برابر با حاصل‌ضرب مساحت قاعده (A) در ارتفاع (L) است:

$$
d m = \frac { M } { A L } \times A d z
$$

$$
d m = \frac { M } { L } d z
$$

با قرار دادن dm در رابطه $$ d I _ x $$، خواهیم داشت:

$$
d I _ x = \frac { ۱ } { ۴ } \frac { M } { L } d z R ^ ۲
$$

اگر محور دوران المان از مرکز جرم استوانه عبور کند، ممان اینرسی آن از قضیه محورهای موازی به دست می‌آید. در اینجا، این قضیه به صورت زیر نوشته می‌شود:

$$ d I = d I _ x + d m d ^ ۲ $$

$$ d I _ x $$ و $$ d m $$ را در مراحل قبلی به دست آوردیم. d، فاصله بین محور مرکزی و محور موازی با آن است. این فاصله را با z نمایش می‌دهیم. به این ترتیب، داریم:

$$ d I = \frac { ۱ } { ۴ } \frac { M } { L } d z R ^ ۲ + \frac { M } { L } d z z ^ ۲ $$

$$
d I = \frac { M R ^ ۲ } { ۴ L } d z + \frac { M } { L } z ^ ۲ d z
$$

اکنون از دو طرف رابطه بالا انتگرال می‌گیریم. به دلیل فرض عبور محور دوران از مرکز جرم (میانه استوانه در طول $$ \frac { L } { ۲ } $$)، بازه انتگرال‌گیری، از $$ - \frac { L } { ۲ } $$ تا $$ \frac { L } { ۲ } $$ است.

$$
\int _ { - \frac { L } { ۲ } } ^ { \frac { L } { ۲ } } d I = \int _ { - \frac { L } { ۲ } } ^ { \frac { L } { ۲ } } \left ( \frac { M R ^ ۲ } { ۴ L } d z + \frac { M } { L } z ^ ۲ d z \right )
$$

$$
I = \int _ { - \frac { L } { ۲ } } ^ { \frac { L } { ۲ } } \frac { M R ^ ۲ } { ۴ L } d z + \int _ { - \frac { L } { ۲ } } ^ { \frac { L } { ۲ } } \frac { M } { L } z ^ ۲ d z
$$

$$ I = \frac { M R ^ ۲ } { ۴ L } \int _ { - \frac { L } { ۲ } } ^ { \frac { L } { ۲ } } d z + \frac { M } { L }\int _ { - \frac { L } { ۲ } } ^ { \frac { L } { ۲ } } z ^ ۲ d z $$

$$
I = \frac { M R ^ ۲ } { ۴ L } [ Z ] _ { - \frac { L } { ۲ } } ^ { \frac { L } { ۲ } } + \frac { M } { L } [ \frac { Z ^ ۳ }{ ۳ } ] _ { - \frac { L } { ۲ } } ^ { \frac { L } { ۲ } }
$$

$$
I = \frac { M R ^ ۲ } { ۴ L } \left [ \frac { L } { ۲ } - \left ( - \frac { L } { ۲ } \right ) \right ] + \frac { M } { ۳ L } \left [ \left ( \frac { L } { ۲ } \right ) ^ ۳ - \left ( - \frac { L } { ۲ } \right ) ^ ۳ \right ]
$$

$$
I = \frac { M R ^ ۲ } { ۴ L } ( L ) + \frac { M } { ۳ L } \left ( \frac { L ^ ۳ } { ۸ } + \frac { L ^ ۳ } { ۸ } \right )
$$

$$
I = \frac { M R ^ ۲ } { ۴ L } ( L ) + \frac { M } { ۳ L } \left ( \frac { ۲ L ^ ۳ } { ۸ } \right )
$$

$$
I = \frac { M R ^ ۲ } { ۴ L } ( L ) + \frac { M } { ۳ L } \left ( \frac { L ^ ۳ } { ۴ } \right )
$$

$$
I = \frac { M R ^ ۲ } { ۴ }+ \frac { M L ^ ۲} { ۱۲ }
$$

در نتیجه، فرمول ممان اینرسی استوانه حول محور عمود بر مرکز جرم اثبات می‌شود:

$$
I _ x = \frac { ۱ } { ۴ } M R ^ ۲ + \frac { ۱ } { ۱۲ } M L ^ ۲
$$

اگر محور دوران را به انتهای استوانه انتقال دهیم، بازه انتگرال‌گیری به ۰ تا L، تغییر می‌کند. در این صورت، ممان اینرسی استوانه حول محور عمودی گذرنده از قطرهای انتهایی از رابطه زیر به دست می‌آید:

$$
I _ x = \frac { ۱ } { ۴ } M R ^ ۲ + \frac { ۱ } { ۳ } M L ^ ۲
$$

ممان اینرسی استوانه توخالی

منظور از استوانه توخالی، استوانه‌ای است که اختلاف بین شعاع داخلی و شعاع خارجی آن، اجتناب‌ناپذیر باشد.

تصویر زیر، یک استوانه توخالی به طول L‌ و جرم M را نمایش می‌دهد.

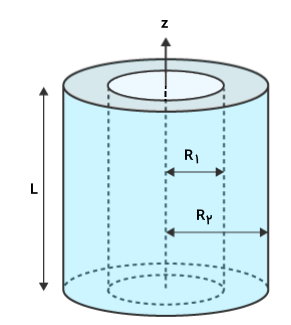
فرمول ممان اینرسی استوانه توخالی حول محور مرکزی به صورت زیر نوشته می‌شود:

$$ I = \frac { ۱ } { ۲ } M ( R _ ۲ ^ ۲ + R _ ۱ ^ ۲ ) $$

• I: ممان اینرسی استوانه توخالی حول محور مرکزی
• M: جرم استوانه توخالی
• R_۱: شعاع داخلی استوانه توخالی
• R_۲: شعاع خارجی استوانه توخالی

ممان اینرسی استوانه توخالی حول محور موازی با محور مرکزی و در یک فاصله مشخص از آن، توسط قضیه محورهای موازی به دست می‌آید.

اثبات فرمول ممان اینرسی استوانه توخالی

به منظور اثبات فرمول ممان اینرسی استوانه توخالی، یک المان کوچک را در راستای محور مرکزی در نظر می‌گیریم. این المان، یک استوانه جدار نازک با ضخامت مقطع dr، مساحت ۲πrdr و ارتفاع L است. جداره المان استوانه‌ای در فاصله r از محور مرکزی قرار دارد.

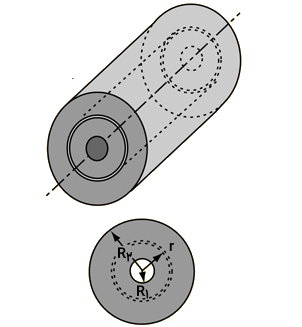
ممان اینرسی استوانه توخالی، از مجموع ممان‌های اینرسی تمام المان‌ها در بازه شعاع داخلی تا شعاع خارجی به دست می‌آید. بر اساس رابطه کلی ممان اینرسی داریم:

$$
I = \int r ^ ۲ d m
$$

اکنون، dm را بر حسب r بازنویسی می‌کنیم. چگالی استوانه توخالی توسط رابطه زیر محاسبه می‌شود:

$$ \rho = \frac { M } { V } $$

• ρ: چگالی استوانه توخالی
• M: جرم استوانه توخالی
• V: حجم استوانه توخالی

می‌دانیم که در اجسام یکنواخت، چگالی کل با چگالی هر یک از المان‌ها برابر است. بنابراین:

$$ \rho = \frac { d m } { d V } $$

• ρ: چگالی یک المان از استوانه توخالی
• dm: جرم یک المان از استوانه توخالی
• dV: حجم یک المان از استوانه توخالی

به این ترتیب، dm برابر است با:

$$ d m = \rho d V $$

حجم المان جزئی استوانه، از ضرب مساحت در ارتفاع آن به دست می‌آید:

$$ d V = ۲πrdr \times L $$

اکنون، معادل dV را درون رابطه dm قرار می‌دهیم:

$$ d m = \rho ۲ \pi r d r L $$

$$ d m = ۲ \pi \rho L r dr $$

پس از قرار دادن این رابطه در فرمول کلی ممان اینرسی، انتگرال را در بازه R_۱ تا R_۲ حل می‌کنیم:

$$
I = \int _ { R _ ۱ } ^ { R _ ۲ } r ^ ۲ ۲ \pi \rho L r dr
$$

$$
I = \int _ { R _ ۱ } ^ { R _ ۲ } r ^ ۳ ۲ \pi \rho L dr
$$

مقادیر ثابت را از انتگرال بیرون می‌کشیم:

$$
I = ۲ \pi \rho L \int _ { R _ ۱ } ^ { R _ ۲ } r ^ ۳ dr
$$

جواب انتگرال برابر است با:

$$
\int _ { R _ ۱ } ^ { R _ ۲ } r ^ ۳dr = \frac { ۱ } { ۴ } r ^ ۴
$$

$$
I = ۲ \pi \rho L \left [ \frac { ۱ } { ۴ } r ^ ۴ \right ] _ { R _ ۱ } ^ { R _ ۲ }
$$

$$
I = ۲ \pi \rho L \left ( \frac { ۱ } { ۴ } R _ ۲ ^ ۴ - \frac { ۱ } { ۴ } R _ ۱ ^ ۴ \right )
$$

از $$ \frac { ۱ } { ۴ } $$ فاکتور می‌گیریم:

$$
I = \frac { ۱ } { ۴ } \times ۲ \pi \rho L \left ( R _ ۲ ^ ۴ - R _ ۱ ^ ۴ \right )
$$

$$
I = \frac { ۱ } { ۲ } \pi \rho L \left ( R _ ۲ ^ ۴ - R _ ۱ ^ ۴ \right )
$$

برای ساده‌تر کردن رابطه بالا، چگالی را بر حسب پارامترهای دیگر بازنویسی می‌کنیم. چگالی استوانه توخالی، نسب جرم (M) به حجم (حاصل‌ضرب سطح مقطع در ارتفاع) است:

$$ \rho = \frac { M } { A L } $$

A، مساحت مقطع استوانه توخالی است که از رابطه زیر به دست می‌آید:

$$ A = \pi ( R _ ۲ ^ ۲ - R _ ۱ ^ ۲ ) $$

به این ترتیب داریم:

$$ \rho = \frac { M } { \pi ( R _ ۲ ^ ۲ - R _ ۱ ^ ۲ ) L } $$

این رابطه درون فرمول I قرار می‌دهیم:

$$
I = \frac { ۱ } { ۲ } \pi \left [ \frac { M } { \pi ( R _ ۲ ^ ۲ - R _ ۱ ^ ۲ ) L} \right ] L \left ( R _ ۲ ^ ۴ - R _ ۱ ^ ۴ \right )
$$

عبارت $$ \left ( R _ ۲ ^ ۴ - R _ ۱ ^ ۴ \right ) $$ را می‌توان به صورت زیر بازنویسی کرد:

$$
\left ( R _ ۲ ^ ۴ - R _ ۱ ^ ۴ \right ) = \left ( R _ ۲ ^ ۲ - R _ ۱ ^ ۲ \right )\left ( R _ ۲ ^ ۲ + R _ ۱ ^ ۲ \right )
$$

بنابراین:

$$
I = \frac { ۱ } { ۲ } \pi \left [ \frac { M } { \pi ( R _ ۲ ^ ۲ - R _ ۱ ^ ۲ ) L} \right ] L \left ( R _ ۲ ^ ۲ - R _ ۱ ^ ۲ \right )\left ( R _ ۲ ^ ۲ + R _ ۱ ^ ۲ \right )
$$

با ساده‌کردن عبارت‌ها، داریم:

$$
I = \frac { ۱ } { ۲ } M \left ( R _ ۲ ^ ۲ + R _ ۱ ^ ۲ \right )
$$

در نتیجه، فرمول ممان اینرسی استوانه توخالی حول محور مرکزی اثبات شد.

ممان اینرسی استوانه جدار نازک

«استوانه جدار نازک» (Thin Walled Cylinder)، یک استوانه توخالی است که دیواره آن، ضخامت بسیار کمی نسبت به شعاع آن دارد. به دلیل کوچک بودن ابعاد دیواره‌ این نوع استوانه، نمی‌توان شعاع داخلی برای آن تعریف کرد.

بنابراین، شعاع خارجی و شعاع خارجی استوانه جدار نازک، برابر با یکدیگر در نظر گرفته می‌شوند. تصویر زیر، یک استوانه جدار نازک به شعاع R و جرم M را نمایش می‌دهد.

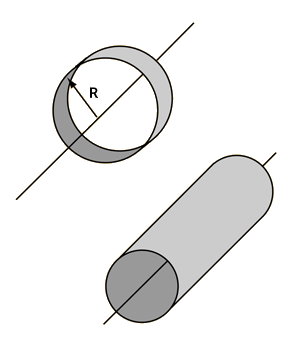
فرمول ممان اینرسی استوانه جدار نازک (استوانه‌ای با ضخامت دیواره کم) حول محور مرکزی، برابر است با:

$$ I = M R ^ ۲ $$

اثبات فرمول ممان اینرسی استوانه جدار نازک

روند اثبات فرمول لختی دورانی استوانه جدار نازک، تفاوت چندانی با روند اثبات فرمول لختی دورانی استوانه توپر و توخالی ندارد. تصویر زیر را در نظر بگیرید.

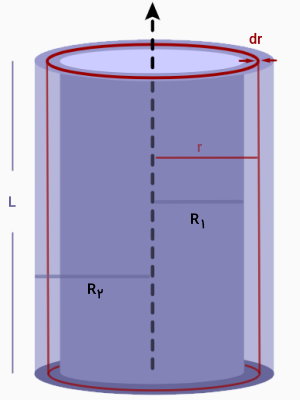
تصویر بالا، پارامترهای یک استوانه را نمایش می‌دهد. پارامترهای هندسی این استوانه عبارت هستند از:

• L: ارتفاع استوانه
• R_۱: شعاع داخلی استوانه
• R_۲: شعاع خارجی استوانه
• dr: ضخامت یک المان جزئی از استوانه (المان استوانه‌ای)
• r: فاصله عمودی المان المان جزئی تا محور دوران مرکزی (شعاع المان)

در بخش‌های قبلی دیدیم که برای یک استوانه توخالی با شعاع داخلی R_۱ و شعاع خارجی R_۲، ممان اینرسی از رابطه زیر به دست می‌آید:

$$
I = \frac { ۱ } { ۲ } M \left ( R _ ۲ ^ ۲ + R _ ۱ ^ ۲ \right )
$$

این رابطه را می‌توانیم به عنوان فرمول کلی ممان اینرسی تمام استوانه‌ها (توپر، توخالی و جدار نازک) در نظر بگیریم. در استوانه توپر، شعاع خارجی برابر با R_۱ و شعاع داخلی برابر با ۰ است.

$$ R _ ۱ = R $$

$$ R _ ۲ = ۰ $$

بنابراین، ممان اینرسی استوانه توپر (I_s) به صورت زیر نوشته می‌شود:

$$ I _ s = \frac { ۱ } { ۲ } M \left ( R _ ۲ ^ ۲ + R _ ۱ ^ ۲ \right ) $$

$$ I _ s = \frac { ۱ } { ۲ } M \left ( ۰ ^ ۲ + R ^ ۲ \right ) $$

$$ I _ s = \frac { ۱ } { ۲ } M \left ( ۰ + R ^ ۲ \right ) $$

$$ I _ s = \frac { ۱ } { ۲ } M R ^ ۲ $$

در استوانه جدار نازک، اختلاف بین شعاع خارجی و داخلی ناچیز است. از این‌رو می‌توان آن‌ها را برابر با یکدیگر در نظر گرفت:

$$ R _ ۱= R _ ۲ = R $$

به این ترتیب، ممان اینرسی استوانه جدار نازک (I_t) برابر است با:

$$ I _ t = \frac { ۱ } { ۲ } M \left ( R _ ۲ ^ ۲ + R _ ۱ ^ ۲ \right ) $$

$$ I _ t = \frac { ۱ } { ۲ } M \left ( R ^ ۲ + R ^ ۲ \right ) $$

$$ I _ t = \frac { ۱ } { ۲ } M \times ۲ R ^ ۲ $$

$$ I _ t = M R ^ ۲ $$

در نتیجه، فرمول لختی دورانی استوانه جدار نازک اثبات می‌شود.

ممان اینرسی میله چگونه بدست می آید ؟

میله، استوانه‌ای با شعاع نسبتا کم و ارتفاع نسبتا زیاد است. به عبارت دیگر، این جسم، یک استوانه کشیده است که می‌توان از ضخامت (شعاع) آن صرف‌نظر کرد. به همین دلیل، ممان اینرسی میله حول محور گذرنده از مرکز قاعده‌ها تعیین نمی‌شود.

برای این جسم، ممان اینرسی حول محورهای گذرنده از قطر مرکزی و قطرهای انتهایی مورد محاسبه قرار می‌گیرد. میله زیر را در نظر بگیرید. این تصویر، یک میله یکنواخت به طول L و جرم M را نمایش می‌دهد.

در مبحث لختی دورانی میله، معمولا دو محور از اهمیت بالایی برخوردار است. یکی از این محورها از مرکز جرم میله (میانه میله) عبور می‌کند و محور دیگر، بر انتهای میله مماس می‌شود.

ممان اینرسی میله حول محور مرکزی، از رابطه زیر به دست می‌آید:

$$ I _ { c m } = \frac { ۱ } { ۱۲ } M L ^ ۲ $$

• I_cm: ممان اینرسی میله حول محور مرکزی
• M: جرم میله
• L: طول میله

اگر محور دوران را به انتهای میله (مماس بر سطوح انتهایی) انتقال دهیم، فرمول ممان اینرسی میله به شکل زیر درمی‌آید:

$$ \frac { ۱ } { ۳ } M R ^ ۲ $$

اثبات فرمول ممان اینرسی میله

به منظور اثبات فرمول ممان اینرسی میله حول محور مرکزی، یک المان جزئی را در فاصله r از محور دوران در نظر می‌گیریم. جرم این المان، dm است. به این ترتیب، طول المان برابر با dr می‌شود.

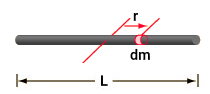
مطابق با رابطه کلی ممان اینرسی، داریم:

$$
I = \int r ^ ۲ d m
$$

برای حل انتگرال بالا، باید عبارت‌های آن را بر حسب r و dr بازنویسی کنیم. می‌دانیم که میله‌ای به طول L، دارای وزن M است. به دلیل یکنواخت بودن میله، نسبت وزن به طول آن، ثابت است. بنابراین:

$$ \frac { M } { L } = { d m } { d r } $$

$$ d m = \frac { M } { L } dr $$

به جای dm در انتگرال، معادل آن را قرار می‌دهیم:

$$
I = \int r ^ ۲ \frac { M } { L } dr
$$

با توجه به محل قرارگیری محور دوران (میانه میله)، بازه انتگرال‌گیری از $$ - \frac { L } { ۲ } $$ تا $$ \frac { L } { ۲ } $$ خواهد بود.

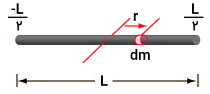
از این‌رو، داریم:

$$
I = \int _ { - \frac { L } { ۲ } } ^ { \frac { L } { ۲ } } r ^ ۲ \frac { M } { L } dr
$$

$$ \frac { M } { L } $$، یک مقدار ثابت است. بنابراین می‌توانیم آن را به پشت انتگرال ببریم:

$$
I = \frac { M } { L } \int _ { - \frac { L } { ۲ } } ^ { \frac { L } { ۲ } } r ^ ۲ dr
$$

انتگرال عبارت $$ r ^ ۲ $$ بر حسب dr، برابر است با:

$$
\int r ^ ۲ dr = \frac { ۱ } { ۳ } r ^ ۳
$$

به این ترتیب داریم:

$$
I = \frac { M } { L } [ \frac { ۱ } { ۳ } r ^ ۳ ] _ { - \frac { L } { ۲ } } ^ { \frac { L } { ۲ } }
$$

$$
I = \frac { M } { ۳ L }\left [ ( \frac { L } { ۲ }) ^ ۳ - ( -\frac { L } { ۲ }) ^ ۳ \right ]
$$

$$
I = \frac { M } { ۳ L }\left [ \frac { L ^ ۳ } { ۸ } - ( -\frac { L ^ ۳ } { ۸ } ) \right ]
$$

$$
I = \frac { M } { ۳ L }\left [ \frac { L ^ ۳ } { ۸ } + \frac { L ^ ۳ } { ۸ } \right ]
$$

$$
I = \frac { M } { ۳ L }\left [ \frac { ۲ L ^ ۳ } { ۸ } \right ]
$$

$$
I = \frac { M } { ۳ L }\left [ \frac { L ^ ۳ } { ۴ } \right ]
$$

$$
I = \frac { M L ^ ۳ } { ۱۲ L }
$$

$$
I = \frac { M L ^ ۲ } { ۱۲ }
$$

$$ I = \frac { ۱ } { ۱۲ } M L ^ ۲ $$

در نتیجه، فرمول ممان اینرسی میله حول محور مرکزی را اثبات کردیم. برای اثبات فرمول ممان اینرسی میله حول محورهای انتهایی، شکل زیر را در نظر بگیرید.

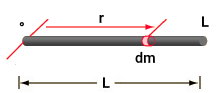
با توجه به شکل بالا، محور دوران در موقعیت انتهایی میله با مختصات ۰ قرار دارد. بنابراین، اگر انتگرال زیر را در بازه ۰ تا L حل کنیم، به فرمول ممان اینرسی میله حول محورهای انتهایی می‌رسیم:

$$
I = \int _ { ۰ } ^ { L } r ^ ۲ \frac { M } { L } dr
$$

$$
I = \frac { M } { L } \int _ { ۰ } ^ { L } r ^ ۲ dr
$$

$$
I = \frac { M } { L } [ \frac { ۱ } { ۳ } r ^ ۳ ] _ { ۰ } ^ { L }
$$

$$
I = \frac { M } { ۳ L } ( L ^ ۳ - ۰ )
$$

$$
I = \frac { M L ^ ۳ } { ۳ L }
$$

$$
I = \frac { M L ^ ۲ } { ۳ }
$$

$$
I = \frac { ۱ } { ۳ } M L ^ ۲
$$

به این ترتیب، فرمول ممان اینرسی میله حول محورهای انتهایی را نیز اثبات کردیم. البته امکان رسیدن به این فرمول، توسط قضیه محورهای موازی نیز وجود داشت.

قضیه محورهای موازی برای ممان اینرسی میله حول محورهای انتهایی

برای به دست آوردن فرمول ممان اینرسی میله حول محورهای انتهایی، از قضیه محورهای موازی استفاده می‌کنیم. بر اساس این قضیه داریم:

$$
I = I _ { c m } + M d ^ ۲
$$

• I: ممان اینرسی حول محور موازی با محور مرکزی
• I_cm: ممان اینرسی حول مرکزی
• M: جرم
• d: فاصله محور دوران با محور مرکزی

اکنون، محوری موازی با محور مرکزی میله و در یک انتهای آن را در نظر می‌گیریم.

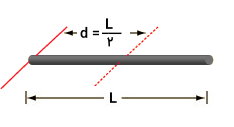
فاصله محور مورد نظر تا محور مرکزی، $$ \frac { L } { ۲ } $$‌ است. بنابراین، داریم:

$$
I = \frac { ۱ } { ۱۲ } M L ^ ۲ + M ( \frac { L } { ۲ } ) ^ ۲
$$

$$
I = \frac { ۱ } { ۱۲ } M L ^ ۲ + \frac { M L ^ ۲} { ۴ }
$$

$$
I = \frac { ۱ } { ۱۲ } M L ^ ۲ + \frac { ۳ M L ^ ۲} { ۱۲ }
$$

$$
I = \frac {۴ M L ^ ۲} { ۱۲ }
$$

$$
I = \frac { M L ^ ۲} { ۳ }
$$

$$
I = \frac { ۱ } { ۳ } M L ^ ۲
$$

در نتیجه، با استفاده از قضیه محورهای موازی، به فرمول ممان اینرسی میله محورهای انتهایی می‌رسیم.

جدول ممان اینرسی استوانه توپر، توخالی و جدار نازک

در این بخش، فرمول‌های محاسبه ممان اینرسی استوانه توپر، توخالی و جدار نازک حول محورهای اصلی دستگاه مختصات سه‌بعدی (محورهای گذرنده از مرکز جرم استوانه) را در قالب یک جدول ارائه می‌کنیم.

جدول زیر فرمول‌های مربوط به ممان اینرسی استوانه توپر و میله حول محورهای مختلف را نمایش می‌دهد.

سوالات متداول در رابطه با ممان اینرسی استوانه

در این بخش، به برخی از پرتکرارترین سوالات در رابطه با ممان اینرسی استوانه به طور مختصر پاسخ می‌دهیم.

تعریف ممان اینرسی استوانه چیست ؟

ممان اینرسی یا لختی دورانی استوانه، معیاری است که توزیع جرم اجسام استوانه‌ای شکل را حول یک محور مشخص نمایش می‌دهد.

کاربرد ممان اینرسی استوانه چیست ؟

ممان اینرسی یا لختی دورانی استوانه، به منظور بررسی مقاومت اجسام استوانه‌ای در برابر شتاب زاویه‌ای به کار می‌رود. این کمیت، در محاسبه مقاومت خمشی و پیچشی نیز کاربرد دارد.

ممان اینرسی استوانه چگونه محاسبه می شود ؟

ممان اینرسی استوانه، با ضرب جرم تمام ذره‌ها در فاصله فاصله‌شان تا محور دوران و جمع این ضرب‌ها به دست می‌آید.

ممان اینرسی استوانه به چه پارامترهایی بستگی دارد ؟

فرمول ممان اینرسی استوانه، به موقعیت دوران و جرم جسم بستگی دارد.

فرمول ممان اینرسی استوانه توپر چیست ؟

فرمول ممان اینرسی استوانه حول محور تقارن گذرنده از مرکز قاعده‌های آن، برابر با I=MR^۲/۲ است.

فرمول ممان اینرسی استوانه توخالی چیست ؟

فرمول ممان اینرسی استوانه توخالی حول محور تقارن گذرنده از مرکز قاعده‌های آن، برابر با I=M(R^۲+R'^۲)/۲ است. R، شعاع خارجی و 'R، شعاع داخلی استوانه را نمایش می‌دهد.

فرمول ممان اینرسی استوانه جدار نازک چیست ؟

فرمول ممان اینرسی استوانه جدار نازک حول محور تقارن گذرنده از مرکز قاعده‌های آن، برابر با I=MR^۲ است.

واحد ممان اینرسی استوانه چیست ؟

لختی دورانی استوانه با واحد کیلوگرم در متر مربع (kg.m^۲) بیان می‌شود. یکای این کمیت در سیستم آمریکایی و بریتانیایی، پوند فوت در مربع ثانیه (lbf.ft.s^۲) است.

رابطه بین ممان اینرسی استوانه با موقعیت محور دوران چگونه است ؟

هر چه محور دوران از مرکز جرم فاصله بگیرید، ممان اینرسی استوانه بیشتر می‌شود.

کمترین ممان اینرسی استوانه حول کدام محور دوران است ؟

کمترین ممان اینرسی استوانه، حول محور گذرنده از مرکز قاعده‌‌های آن است.