کاربرد مشتق – به زبان ساده

وبلاگ فرادرس، بستری است که در آن مجموعه مطالب ریاضیات در شاخه‌های گوناگون توضیح داده شده‌اند. برای نمونه مجموعه مطالب انتگرال در این‌جا توضیح داده شده‌اند. از طرفی در مطلب جداگانه، مفاهیم مشتق و کاربرد‌های آن در ریاضی را شرح دادیم. در همین راستا در این مطلب قصد داریم تا اندکی از ریاضیات فاصله گرفته و کاربرد مشتق در کسب و کار را توضیح دهیم.

کاربرد مشتق

در مواردی ممکن است پولی در اختیار داشته باشید. اما سرمایه‌گذاری آن در بستر‌های مختلف نتایج مختلفی را نیز در پی خواهد داشت. در حقیقت باید حالت بهینه سرمایه‌گذاری را بدست آورد. از این رو در اولین مثال قصد داریم تا مسئله‌ای از جنس بهینه‌سازی را توضیح دهیم.

مثال ۱

مجموعه‌ای آپارتمانی که شامل ۲۵۰ واحد برای اجاره است را در نظر بگیرید. اگر $$x$$ واحد اجاره داده شود، در این صورت سود ماهیانه مطابق با رابطه زیر بدست خواهد آمد.

$$\large P \left ( x \right ) = - 8 { x ^ 2 } + 3200 x - 80,000$$

سوال: اگر شما صاحب این آپارتمان بودید، چند واحد اجاره می‌دادید؟

پاسخ: بدیهی است که هر شخصی به دنبال بیشترین سود است. از این رو در این مسئله نیز باید بیشترین سود محاسبه شود. این جا است که می‌توان از مشتق استفاده کرد. جهت ماکزیمم کردن سود یا همان $$P(x)$$،‌ کافی است از تابع سود ارائه شده، مطابق با رابطه زیر مشتق گرفته و ماکزیمم را بدست بیاوریم.

$$P ^ { \prime } \left ( x \right ) = - 16 x + 3200 \hspace{0.2in} \Rightarrow \hspace {0.1in} 3200 - 16 x = 0\hspace {0.1in} \Rightarrow \hspace{0.25in} x = \frac { { 3200 } } {{ 16 } } = 200$$

عدد بدست آمده مقداری صحیح و مثبت است. در ادامه مقدار سود به ازای سه مقدار مختلف محاسبه شده است.

$$P \left ( 0 \right ) = - 80,000 \ \ , \hspace{0.5in} P \left ( { 200 } \right ) = 240,000 \ \ , \hspace {0.5in} P \left ( { 250 } \right ) = 220,000$$

با مقایسه مقادیر فوق می‌توان دید که اجاره دادن ۲۰۰ واحد، بیشترین سود را دارد.

مثال ۱ نشان داد که همواره الزاما اجاره دادن تمامی واحد‌ها منجر به کسب بیشترین سود نخواهد شد. از این رو توجه داشته باشید که همواره نمی‌توان با استفاده از تمامی منابع بیشترین سود ممکن را بدست آورد. در ادامه مثالی دیگر ارائه شده که به جای سود، میزان هزینه، بهینه شده است.

مثال ۲

یک کارخانه، در بیشترین بار کاری، این قابلیت را دارد که روزانه ۶۰۰۰ نمونه از یک کالا را تولید کند. از طرفی هزینه تولید روزانه $$x$$ نمونه از این کالاها برابرند با:

$$\large C \left ( x \right ) = 250,000 + 0.08 x + \frac { { 200,000,000 } } { x }$$

سوال: به نظر شما به منظور مینیمم کردن هزینه تولید، روزانه چه تعداد از کالای مذکور را باید تولید کرد.

پاسخ: از صورت سوال می‌توان دریافت که باید مینیمم مقدار $$C ( x )$$ را در بازه $$0 \le x \le 60,000$$ یافت. بدین منظور در ادامه نقاط مینیمم این تابع در بازه مذکور بدست آمده است.

$$C ^ { \prime } \left( x \right) = 0.08 - \frac { { 200,000,000 } } { { { x ^ 2 } } } \hspace {0.5in} \Rightarrow \hspace {0.5in} C ^ { \prime \prime } \left ( x \right ) = \frac { { 400,000,000 } } { { { x ^ 3 } } }$$

توجه داشته باشید که مقدار منفی بدست آمده در بالا معنی ندارد، چون مقدار منفی هزینه، بی‌معنی است. از طرفی به ازا‌ی مقادیر $$x > 0$$، مشتق دوم مثبت است؛ بنابراین ۵۰۰۰۰ تولید، مقدار مینیمم مطلق هزینه را به ما خواهد داد.

در مثال‌های ۱ و ۲ با کمیت‌هایی سر و کار داشتیم که یکی از آن‌ها مینیمم و دیگری ماکزیمم شدند. اما همواره مسائلی از جنس کسب و کار با این سوالات مواجه نیستند که نیازمند ماکزیمم و مینیمم کردن باشند.

مثال ۳

هزینه تولید هفتگی $$x$$ نمونه از یک کالا برابر است با:

$$\large C \left ( x \right ) = 500 + 350 x - 0.09 { x ^ 2 } \, ,\,\,\,\,\,\,0 \le x \le 1000$$

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

با فرض فوق، به سوالات زیر پاسخ دهید.

1. هزینه تولید کالای ۳۰۱ام چقدر است؟
2. نرخ تغییرات هزینه در هنگام تولید کالای ۳۰۰ام چقدر است؟

پاسخ ۱: توجه داشته باشید که نمی‌توان به راحتی و با محاسبه $$C \left ( {3 01 } \right )$$ هزینه تولید این کالا را یافت؛ چراکه این مقدار به معنای هزینه تمامی ۳۰۱ کالا است. در حقیقت باید اختلاف میان هزینه کالای ۳۰۱ام و ۳۰۰ام محاسبه شوند. بدین منظور داریم:

$$C \left ( { 301 } \right ) - C \left ( { 300 } \right ) = 97,695.91 - 97,400.00 = 295.91$$

پاسخ ۲: به منظور پاسخ به این سوال کافی است مشتق تابع هزینه $$C$$ را در ۳۰۱ بدست آوریم. در نتیجه داریم:

$$\large C ^ { \prime } \left ( x \right ) = 350 - 0.18 x \hspace {0.5in} \Rightarrow \hspace {0.5in} C ^ { \prime } \left ( { 300 } \right ) = 296.00$$

بنابراین هزینه تولید کالای ۳۰۱ام، برابر با ۲۹۶ است. جالب است بدانید که در کسب و کار، به عدد بدست آمده «هزینه نهایی» (Marginal Cost) نیز گفته می‌شود. هزینه نهایی در حقیقت نشان دهنده تغییرات هزینه کل به ازای تولید کالای جدید است. توجه داشته باشید که $$C ^ { \prime } \left ( n \right )$$ نشان دهنده هزینه مطلقِ تولید کالای $$n+1$$ام است.

حال فرض کنید هدف ما بررسی هزینه میانگین است. اگر تابعی همچون $$C(x)$$ نشان دهنده تابع هزینه باشد، در این صورت مقدار میانگین هزینه تولید $$x$$ کالا برابر است با:

$$\large \overline { C } \left ( x \right ) = \frac { { C \left ( x \right ) } } { x }$$

برای نمونه فرض کنید هزینه تولید روزانه $$x$$ کالا برابر با تابع زیر باشد.

$$\large C \left ( x \right ) = 2500 - 10 x - 0.01 { x ^ 2 } + 0.0002 { x ^ 3 }$$

در این صورت نمودار هزینه میانگین برای این تابع هزینه برابر است با:

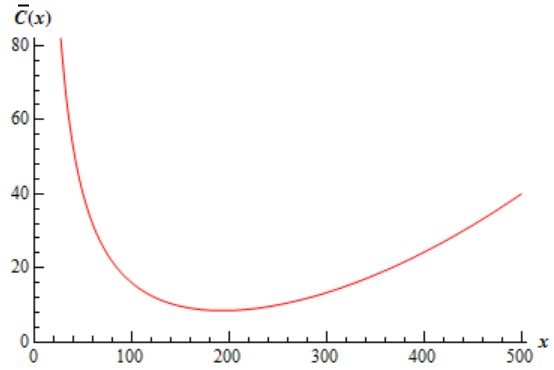
همان‌طور که از نمودار فوق نیز دیده می‌شود، نمودار میانگین هزینه دارای مینیمم مطلق است. بنابراین می‌توان با استفاده از مشتقِ $$\overline C ^ { \prime } \left ( x \right ) = 0$$، مقدار مینیمم هزینه میانگین را بدست آورد. به منظور بدست آوردن این نقطه، کافی است مشتق زیر را برابر با صفر قرار دهیم.

$$\large \overline { C } ^ { \prime } \left ( x \right ) = \frac { { x \, C ^ { \prime } \left ( x \right ) - C \left( x \right ) } } { { { x ^ 2 } } }$$

$$\large { \Rightarrow \ x C ^ { \prime } ( x ) - C ( x ) = 0 \ \ \Rightarrow \ \ C ^ { \prime } ( x ) = \frac { C ( x ) }{ x } = \bar C ( x ) }$$

عبارت فوق نشان می‌دهد زمانی که نرخ تغییرات هزینه کل برابر با میانگین هزینه باشد، میانگین هزینه مینیمم خواهد شد. حال می‌خواهیم در مورد توابع درآمد و سود بحث کنیم. در ابتدا فرض کنید قیمت قابل فروش برای یک کالا برابر با تابع $$p \left ( x \right )$$ باشد. این تابع را تابعِ قیمت نیز می‌نامند. در این صورت تابع درآمد مطابق با رابطه زیر قابل محاسبه است.

$$\large R \left ( x \right) = x \, p \left ( x \right )$$

با کم کردن تابع هزینه از تابع درآمد، تابع سود مطابق با رابطه زیر بدست خواهد آمد.

$$P \left ( x \right ) = R \left ( x \right ) - C \left ( x \right ) = x \, p \left ( x \right ) - C \left ( x \right )$$

توجه داشته باشید که علامت‌های $$P$$ (تابع سود) و $$p$$ (تابع قیمت) نشان دهنده مفاهیم متفاوتی هستند. در آخر با مشتق‌گیری، توابعِ درآمد نهایی ($$R ^ { \prime } \left ( x \right )$$) و سود نهایی ($$P ^ { \prime } \left ( x \right )$$) نیز قابل محاسبه هستند.

مثال ۴

هزینه هفتگی به منظور تولید $$x$$ نمونه از یک کالای خاص برابر است با:

$$\large C \left ( x \right ) = 75,000 + 100 x - 0.03 { x ^ 2 } + 0.000004 { x ^ 3 } \hspace {0.5in} 0 \le x \le 10000$$

از طرفی تابع قیمت به ازای تولید هر کالا نیز مطابق با رابطه زیر قابل توصیف است.

$$\large p \left ( x \right ) = 200 - 0.005 x \hspace {0.5in} 0 \le x \le 10000$$

سوال: با این فرض، تابع نهایی هزینه، تابع نهایی درآمد و تابع نهایی سود را در حالتی که ۲۵۰۰ نمونه یا ۷۵۰۰ نمونه از کالا فروخته شده، چقدر خواهند بود؟

پاسخ: در اولین قدم باید توابع مورد نیاز را به صورت زیر بدست آوریم. توابع درآمد و سود برابرند با:

$$\large \begin {align*} R \left( x \right) & = x \left ( { 200 - 0.005 x } \right) = 200x - 0.005 { x ^ 2 } \\ P\left( x \right) & = 200 x - 0.005 { x ^ 2 } - \left ( { 75,000 + 100x - 0.03{x^2} + 0.000004 { x ^ 3 } } \right ) \\ & = - 75,000 + 100x + 0.025 { x ^ 2 } - 0.000004 { x ^ 3 } \end {align*}$$

بنابراین توابع نهایی، به سادگی و با مشتق‌گیری از توابع فوق بدست می‌آیند.

$$\large \begin{align*} C ^ { \prime } \left( x \right) & = 100 - 0.06x + 0.000012 { x ^ 2 } \\ R ^ { \prime } \left ( x \right ) & = 200 - 0.01x\\ P ^ { \prime } \left( x \right) & = 100 + 0.05 x - 0.000012 { x ^ 2 } \end {align*}$$

توابع نهایی زمانی که ۲۵۰۰ نمونه از کالا فروخته شده‌اند، برابرند با:

$$\large C ^ { \prime } \left ( { 2500 } \right) = 25 \hspace {0.5in} R ^ { \prime } \left( { 2500 } \right ) = 175 \hspace {0.5in} P ^ { \prime } \left ( { 2500 } \right ) = 150$$

همین توابع در حالتی که ۷۵۰۰ نمونه از کالا‌ها فروخته شده باشند، برابرند با:

$$\large {C ^ { \prime } \left ( { 7500 } \right) = 325\hspace{0.5in} R ^ { \prime } \left( { 7500 } \right ) = 125 \hspace {0.5in} P ^ { \prime } \left( { 7500 } \right ) = - 200}$$

بنابراین هزینه تولید کالای ۲۵۰۱ام برابر با ۲۵ دلار و سود ناشی از تولید آن ۱۵۰ دلار خواهد بود. این در حالی است که هزینه تولید کالای ۷۵۰۱ام از درآمد ناشی از فروش آن بیشتر خواهد بود.

هدف اصلی در محاسبات رسیدن به بیشترین سود است. بدین منظور کافی است ماکزیمم تابع $$P(x)$$ یافته شود. در نتیجه باید مشتق آن برابر با صفر قرار داده شود. این مشتق در ادامه بیان شده است.

$$P ^ { \prime } \left( x \right) = R ^ { \prime } \left( x \right) - C ^ { \prime } \left( x \right) = 0 \hspace {0.5in} \Rightarrow \hspace{0.5in} R ^ { \prime } \left( x \right) = C ^ { \prime } \left ( x \right )$$

با توجه به این که سود مقداری ماکزیمم دارد، بنابراین خمیدگی نمودار آن به سمت پایین خواهد بود. در نتیجه می‌توان رابطه بین مشتقات دوم را به صورت زیر بیان کرد:

$$\large P ^ { \prime\prime } \left( x \right ) = R ^ { \prime\prime } \left( x \right) - C ^ { \prime\prime } \left( x \right ) < 0 \hspace {0.5in} \Rightarrow \hspace{0.5in} R ^ { \prime\prime } \left( x \right ) < C ^ { \prime\prime } \left ( x \right )$$

بنابراین با فرضِ $$R ^ { \prime \prime } \left ( x \right ) < C ^ { \prime \prime } \left ( x \right )$$، زمانی سود ناشی از تولید و فروش کالاها ماکزیمم می‌شود که رابطه $$R ^ { \prime } \left ( x \right ) = C ^ { \prime } \left ( x \right )$$ برقرار باشد.
در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• مجموعه آموزش‌های ریاضیات و فیزیک پایه
• مشتق — به زبان ساده
• فهرست مطالب ریاضی وبلاگ فرادرس
• انتگرال - به زبان ساده

^^