مشتق در مختصات قطبی — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزش‌های پیشین مجله فرادرس، دستگاه مختصات قطبی را معرفی و نحوه نمایش نقاط و توابع را در این مختصات بیان کردیم. در این آموزش، مشتق در مختصات قطبی را توضیح می‌دهیم. همچنین، با توابع و نمودارهای قطبی معروف، آشنا خواهیم شد.

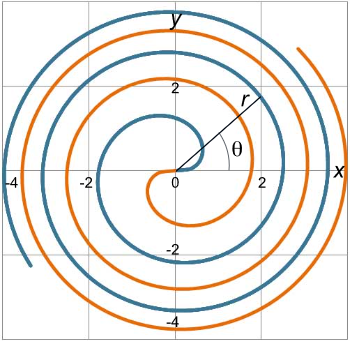
همان‌طور که می‌دانیم، موقعیت نقاط در صفحه را می‌توان در دستگاه‌های مختصات مختلف توصیف کرد. در کنار دستگاه مختصات کارتزین، از دستگاه مختصات قطبی نیز استفاده‌های فراوانی می‌شود. در این دستگاه مختصات، موقعیت نقطه $$M$$ را می‌توان با دو عدد نشان داد:

•  $$r$$ که طول بردار شعاعی از مبدأ تا نقطه $$M$$ است.

• زاویه قطبی $$\theta$$ که بین خط $$OM$$ و جهت مثبت محور $$x$$ است. زاویه $$\theta$$ در خلاف جهت عقربه‌های ساعت سنجیده می‌شود.

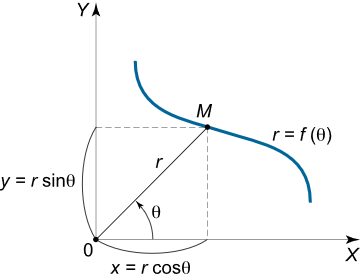
معادله $$r = f\left( \theta \right)$$ که طول بردار شعاعی $$r$$ را براساس زاویه قطبی $$\theta$$ بیان می‌کند، یک منحنی در صفحه است که منحنی معادله قطبی نامیده می‌شود.

برای مثال، مارپیچ ارشمیدس، با معادله قطبی زیر توصیف می‌شود:

$$r = a\theta$$

که در آن، $$a$$ پارامتری است که تراکم یا نزدیکی دورهای مارپیچ را نشان می‌دهد.

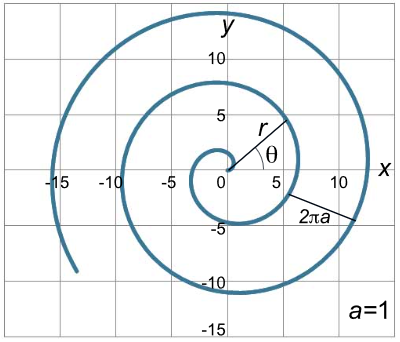
فاصله بین هر دو دور مارپیچ ارشمیدس، ثابت و برابر $$2\pi a$$ است.

فرمول عمومی تبدیل مختصات قطبی $$\left( {r,\theta } \right)$$ به مختصات کارتزین $$\left( {x,y} \right)$$ به‌صورت زیر است:

$${x = r\cos \theta ,\;\;}\kern-0.3pt{y = r\sin \theta .}$$

اگر یک منحنی با معادله قطبی $$r = f\left( \theta \right)$$ داشته باشیم، می‌توان آن را در مختصات کارتزین به‌صورت زیر بیان کرد:

$$\left\{
\begin{aligned}
x &= f\left( \theta \right)\cos\theta \\
y &= f\left( \theta \right)\sin\theta
\end{aligned}
\right.$$

همان‌طور که می‌بینیم، می‌توان معادلات پارامتری منحنی را نوشت که در آن، زاویه $$\theta$$ نقش پارامتر $$t$$ را بازی می‌کند. در این حالت، مشتق منحنی قطبی با فرمول مشتق یک تابع پارامتری بیان می‌شود:

$${\frac{{dy}}{{dx}} = {y’_x} = \frac{{{y’_\theta }}}{{{x’_\theta }}} }
= {\frac{{{{\left( {f\left( \theta \right)\sin \theta } \right)}^\prime }}}{{{{\left( {f\left( \theta \right)\cos\theta } \right)}^\prime }}} }
= {\frac{{f’\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f’\left( \theta \right)\cos\theta – f\left( \theta \right)\sin \theta }}.}$$

مثال‌های زیر، نحوه مشتق‌گیری در مختصات قطبی را بهتر نشان می‌دهند.

مثال ۱: مارپیچ ارشمیدس

مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$ مارپیچ ارشمیدس را محاسبه کنید.

حل: معادله مارپیچ ارشمیدس به‌صورت زیر است:

$$r = f\left( \theta \right) = a\theta .$$

مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$ نیز به‌شکل زیر محاسبه می‌شود:

$${\frac{{dy}}{{dx}} = {y’_x} = \frac{{{y’_\theta }}}{{{x’_\theta }}} }
= {\frac{{f’\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f’\left( \theta \right)\cos\theta – f\left( \theta \right)\sin \theta }}.}$$

اگر تابع $$f\left( \theta \right)$$ را در عبارت بالا جایگذاری کنیم، داریم:

$${\frac{{dy}}{{dx}} }={ \frac{{{{\left( {a\theta } \right)}^\prime }\sin \theta + a\theta \cos\theta }}{{{{\left( {a\theta } \right)}^\prime }\cos\theta – a\theta \sin \theta }} }
= {\frac{{a\sin \theta + a\theta \cos \theta }}{{a\cos \theta – a\theta \sin \theta }} }
= {\frac{{\sin \theta + \theta \cos \theta }}{{\cos \theta – \theta \sin \theta }}.}$$

در ادامه، صورت و مخرج عبارت اخیر را بر $${\cos \theta }$$ تقسیم می‌کنیم (با فرض $$\theta \ne \large\frac{\pi }{2}\normalsize + \pi n,\,n \in \mathbb{Z}$$). در نتیجه، عبارت زیر برای مشتق به‌دست می‌آید:

$${\frac{{dy}}{{dx}} }={ \frac{{\tan\theta + \theta }}{{1 – \theta \tan \theta }}.}$$

همچنین، فرمول اخیر را می‌توان با استفاده از اتحاد مثلثاتی زیر ساده‌تر کرد:

$${\tan \left( {\alpha + \beta } \right) }={ \frac{{\tan \alpha + \tan \beta }}{{1 – \tan \alpha \cdot \tan \beta }}.}$$

زاویه $$\theta$$ را به‌صورت زیر نمایش می‌دهیم:

$$\theta = \tan \left( {\arctan\theta } \right).$$

در نهایت، پاسخ این مثال به‌صورت زیر به‌دست می‌آید:

$${\frac{{dy}}{{dx}} }={ \frac{{\tan\theta + \theta }}{{1 – \theta \tan \theta }} }
= {\frac{{\tan\theta + \tan \left( {\arctan\theta } \right)}}{{1 – \tan \theta \cdot \tan \left( {\arctan\theta } \right)}} }
= {\tan \left( {\theta + \arctan\theta } \right).}$$

از این مثال می‌توان این نتیجه را گرفت که مشتق مارپیچ ارشمیدس به شعاع $$r$$ بستگی ندارد. این موضوع، ویژگی خودتشابهی مارپیچ ارشمیدس را نشان می‌دهد.

در صورت علاقه به یادگیری روش‌های تعیین مشتق توابع مختلف، مطالعه مطلب «فرمول‌های مشتق مهم + سوال با جواب و دانلود PDF» را به شما پیشنهاد می‌کنیم.

مثال ۲: دل‌گون

مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$ یک دل‌گون را با معادله زیر به‌دست آورید:

$$r = f\left( \theta \right) = a\left( {1 + \cos \theta } \right).$$

حل: ابتدا مشتق تابع قطبی را حساب می‌کنیم:

$${f’\left( \theta \right) = {\left( {a\left( {1 + \cos \theta } \right)} \right)^\prime } }
= { – a\sin \theta .}$$

مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$ منحنی نیز به‌صورت زیر است:

$${\frac{{dy}}{{dx}} = {y’_x} = \frac{{{y’_\theta }}}{{{x’_\theta }}} }
= {\frac{{f’\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f’\left( \theta \right)\cos\theta – f\left( \theta \right)\sin\theta }} } \\
= {\frac{{ – {{\sin }^2}\theta + \cos \theta + {{\cos }^2}\theta }}{{ – \sin \theta \cos \theta – \sin \theta – \sin \theta \cos \theta }}}$$

با استفاده از اتحادِ

$${\cos 2\theta = {\cos ^2}\theta – {\sin ^2}\theta ,\;\;}\kern-0.3pt
{\sin 2\theta = 2\sin \theta \cos \theta ,}$$

داریم:

$$\frac{{dy}}{{dx}} = – \frac{{\cos 2\theta + \cos \theta }}{{\sin 2\theta + \sin \theta }}.$$

این بار از دو اتحاد مثلثاتی دیگر استفاده خواهیم کرد:

$${{\cos \alpha + \cos \beta }={ 2\cos \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha – \beta }}{2}}},$$

$${{\sin \alpha + \sin \beta }={ 2\sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha – \beta }}{2}.}}$$

و مشتق را به‌شکل زیر ساده می‌کنیم:

$$\require{cancel}
{\frac{{dy}}{{dx}} = – \frac{{\cos 2\theta + \cos \theta }}{{\sin 2\theta + \sin \theta }} }
= { – \frac{{2\cos \frac{{2\theta + \theta }}{2}\cos \frac{{2\theta – \theta }}{2}}}{{2\sin \frac{{2\theta + \theta }}{2}\cos \frac{{2\theta – \theta }}{2}}} } \\
= { – \frac{{\cos \frac{{3\theta }}{2}\cancel{\cos \frac{\theta }{2}}}}{{\sin \frac{{3\theta }}{2}\cancel{\cos \frac{\theta }{2}}}} }
= { – \cot \frac{{3\theta }}{2}.}$$

مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$ در شرایط زیر تعریف می‌شود:‌

$${\left\{ \begin{array}{l}
\cos\frac{\theta }{2} \ne 0\\
\sin \frac{{3\theta }}{2} \ne 0
\end{array} \right.,\;\;}\Rightarrow
{\left\{ \begin{array}{l}
\frac{\theta }{2} \ne \frac{\pi }{2} + \pi n\\
\frac{{3\theta }}{2} \ne \pi k
\end{array} \right.,\;\;}\Rightarrow
{\left\{ \begin{array}{l}
\theta \ne \pi + 2\pi n,\;n \in \mathbb{Z}\\
\theta \ne \frac{2}{3}\pi k,\;k \in \mathbb{Z}
\end{array} \right..}$$

در بازه $$\left( {-\pi,\pi} \right)$$، شرایط فوق معادل $$\theta = – \pi$$، $$\theta=– \frac{{2\pi }}{3}$$، $$\theta=0$$، $$\theta=\frac{{2\pi }}{3}$$ و $$\theta=\pi$$ است. مشتق دل‌گون در این نقاط وجود ندارد.

نمودار دل‌گون شکل زیر، شبیه یک قلب است (واژه انگلیسی cardioid به‌معنی دل‌گون از معادل یونانی آن به‌معنی قلب آمده است) و ویژگی‌های منحصربه‌فردی دارد.

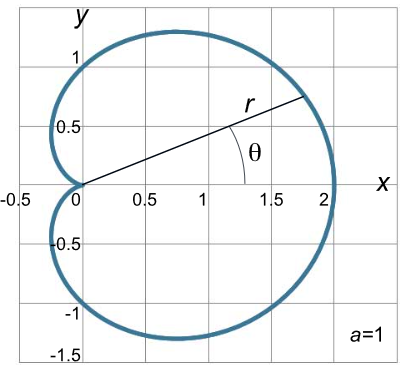
شکل‌های زیبای ریاضی و ساختارهایی با اَشکال مشابه در زمینه‌های مختلف وجود دارند که در نگاه اول بدون ارتباط با یک‌دیگر به‌نظر می‌رسند. شکل زیر، مجموعه فراکتال یا برخال مندلبرو را نشان می‌دهد که از دل‌گون تشکیل شده است.

مثال ۳: مارپیچ لگاریتمی

مشتق مارپیچ لگاریتمی زیر را به‌دست آورید ($$a$$ و $$b$$ اعداد حقیقی هستند):

$$r = f\left(\theta\right)=ae^{b\theta}$$

حل: ابتدا $$f’\left( \theta \right)$$ را محاسبه می‌کنیم:

$${f’\left( \theta \right)} = {\left( {a{e^{b\theta }}} \right)^\prime } = {ab{e^{b\theta }}.}$$

با قرار دادن عبارت بالا در مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$ داریم:

$${\frac{{dy}}{{dx}} = {y’_x} = \frac{{{y’_\theta }}}{{{x’_\theta }}} }
= {\frac{{f’\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f’\left( \theta \right)\cos\theta – f\left( \theta \right)\sin\theta }} }\\
= {\frac{{{{\left( {a{e^{b\theta }}} \right)}^\prime }\sin \theta + a{e^{b\theta }}\cos\theta }}{{{{\left( {a{e^{b\theta }}} \right)}^\prime }\cos\theta – a{e^{b\theta }}\sin\theta }} } \\
= {\frac{{ab{e^{b\theta }}\sin \theta + a{e^{b\theta }}\cos\theta }}{{ab{e^{b\theta }}\cos\theta – a{e^{b\theta }}\sin\theta }} } \\
= {\frac{{b\sin \theta + \cos\theta }}{{b\cos\theta – \sin\theta }} } \\
= {\frac{{b\tan \theta + 1}}{{b – \tan \theta }} }
= {\frac{{\tan \theta + \frac{1}{b}}}{{1 – \tan \theta \cdot \frac{1}{b}}}.}$$

در ادامه، از اتحادهای زیر کمک می‌گیریم:

$${\frac{1}{b} }={ \tan \left( {\arctan \frac{1}{b}} \right)}$$

$${\tan \left( {\alpha + \beta } \right) }={ \frac{{\tan \alpha + \tan \beta }}{{1 – \tan \alpha \cdot \tan \beta }}.}$$

نتیجه نهایی به‌صورت زیر است:

$${\frac{{dy}}{{dx}} }={ \frac{{\tan \theta + \frac{1}{b}}}{{1 – \tan \theta \cdot \frac{1}{b}}} } \\
= {\frac{{\tan \theta + \tan \left( {\arctan \frac{1}{b}} \right)}}{{1 – \tan \theta \cdot \tan \left( {\arctan \frac{1}{b}} \right)}} }\\
= {\tan \left( {\theta + \arctan \frac{1}{b}} \right).}$$

نمودار مارپیچ لگاریتمی در شکل زیر نشان داده شده است.

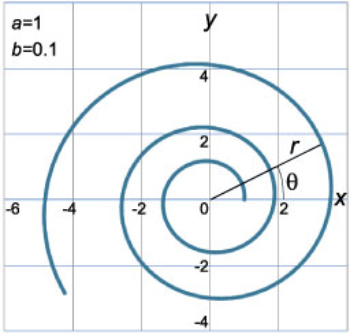
این شکل را می‌توان در طبیعت یافت. برای مثال، شکل پوست نرم‌تنان و برخی کهکشان‌ها مارپیچ لگاریتمی است. شکل زیر کهکشان مارپیچی M81 را نشان می‌دهد.

مثال 4: دایره

مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$ دایره را محاسبه کنید و مقادیر آن را برای زوایای قطبی $$\theta = {\large\frac{\pi }{4}\normalsize}$$ و $${\large\frac{{3\pi }}{4}\normalsize}$$ به‌دست آورید.

حل: معادله یک دایره در مختصات قطبی به‌شکل ساده زیر است:

$$r = f\left( \theta \right) = R$$

که در آن، $$R$$ شعاع دایره است.

از آن‌جایی که $$f’\left( \theta \right) = 0$$، می‌توانیم به‌سادگی مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$ دایره را محاسبه کنیم:

$${\frac{{dy}}{{dx}} = {y’_x} = \frac{{{y’_\theta }}}{{{x’_\theta }}} } \\
= {\frac{{f’\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f’\left( \theta \right)\cos\theta – f\left( \theta \right)\sin\theta }} } \\
= {\frac{{0 \cdot \sin \theta + R\cos\theta }}{{0 \cdot \cos\theta – R\sin\theta }} } \\
= { – \cot \theta .}$$

در حالت خاص، برای زوایای $$\large\frac{\pi }{4}\normalsize$$ و $$\large\frac{3\pi }{4}\normalsize$$، مشتق برابر است با:

$${{\frac{{dy}}{{dx}}\left( {\theta = \frac{\pi }{4}} \right) }={ – \cot\frac{\pi }{4} = – 1,\;\;}}\kern-0.3pt \\
{{\frac{{dy}}{{dx}}\left( {\theta = \frac{{3\pi }}{4}} \right) }={ – \cot\frac{{3\pi }}{4} = 1.}}$$

همان‌طور که می‌دانیم، مقدار مشتق در یک نقطه، برابر با شیب خط مماس بر آن نقطه روی منحنی است. شکل بالا این موضوع را نشان می‌دهد.

مثال ۵: پروانه برنولی

مشتق پروانه برنولی را که به‌فرم زیر است، پیدا کنید:

$${r^2} = \cos 2\theta$$

حل: منحنی را برای زوایای زیر در نظر می‌گیریم:

$$\cos 2\theta \gt 0$$

اگر نامعادله فوق را حل کنیم، داریم:

$${\cos 2\theta \gt 0,\;\;}\Rightarrow
{ – \frac{\pi }{2} + 2\pi n \lt 2\theta \lt \frac{\pi }{2} + 2\pi n,}\\
\Rightarrow { – \frac{\pi }{4} + \pi n \lt \theta \lt \frac{\pi }{4} + \pi n,\;\;}\kern-0.3pt{n \in \mathbb{Z}.}$$

بازه کران‌دار $$– {\large\frac{\pi }{4}\normalsize} \lt \theta \lt {\large\frac{\pi }{4}\normalsize}$$ را انتخاب می‌کنیم که یک طرف پروانه برنولی است.

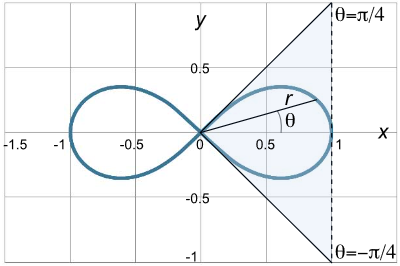
در بازه مذکور، معادله منحنی را می‌توان به‌صورت زیر نوشت:

$$r = f\left( \theta \right) = \sqrt {\cos 2\theta }$$

اکنون مشتق این تابع را محاسبه می‌کنیم:

$${f’\left( \theta \right) = {\left( {\sqrt {\cos 2\theta } } \right)^\prime } }
= {\frac{1}{{2\sqrt {\cos 2\theta } }} \cdot {\left( {\cos 2\theta } \right)^\prime } } \\
= {\frac{1}{{2\sqrt {\cos 2\theta } }} \cdot \left( { – \sin 2\theta } \right) \cdot 2 }
= { – \frac{{\sin 2\theta }}{{\sqrt {\cos 2\theta } }}.}$$

در نتیجه، مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$ را می‌توان به‌صورت زیر محاسبه کرد:

$${\frac{{dy}}{{dx}} = {y’_x} = \frac{{{y’_\theta }}}{{{x’_\theta }}} }
= {\frac{{f’\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f’\left( \theta \right)\cos\theta – f\left( \theta \right)\sin\theta }} } \\
= {\frac{{\left( { – \frac{{\sin 2\theta }}{{\sqrt {\cos 2\theta } }}} \right)\sin \theta + \sqrt {\cos 2\theta } \cos\theta }}{{\left( { – \frac{{\sin 2\theta }}{{\sqrt {\cos 2\theta } }}} \right)\cos\theta – \sqrt {\cos 2\theta } \sin\theta }} } \\
= { – \frac{{\frac{{\cos 2\theta \cos \theta – \sin 2\theta \sin \theta }}{{\cancel{\sqrt {\cos 2\theta }} }}}}{{\frac{{\sin 2\theta \cos \theta + \cos 2\theta \sin \theta }}{{\cancel{\sqrt {\cos 2\theta }} }}}} }
= { – \frac{{\cos 2\theta \cos \theta – \sin 2\theta \sin \theta }}{{\sin 2\theta \cos \theta + \cos 2\theta \sin \theta }}.}$$

اتحادهای زیر را در نظر بگیرید:

$${{\cos\left( {\alpha + \beta } \right) }={ \cos \alpha \cos \beta }-{ \sin \alpha \sin \beta ,\;\;}}\kern0pt \\
{{\sin \left( {\alpha + \beta } \right) }={ \sin \alpha \cos \beta }+{ \cos \alpha \sin \beta.}}$$

صورت و مخرج عبارت فوق را می‌توان با استفاده از اتحادهای بالا ساده کرد:

$${\frac{{dy}}{{dx}} }={ – \frac{{\cos 2\theta \cos \theta – \sin 2\theta \sin \theta }}{{\sin 2\theta \cos \theta + \cos 2\theta \sin \theta }} } \\
= { – \frac{{\cos \left( {2\theta + \theta } \right)}}{{\sin \left( {2\theta + \theta } \right)}} }
= { – \frac{{\cos 3\theta }}{{\sin 3\theta }} }={ – \cot 3\theta .}$$

توجه کنید که تابع $$\cot 3\theta$$ در نقاط زیر تعریف نشده است:

$${3\theta = \pi n,\;\;}\Rightarrow
{\theta = \frac{{\pi n}}{3},\;\;}\kern-0.3pt{n \in \mathbb{Z}\;\;}\\
\Rightarrow
{\theta = 0, \pm \frac{\pi }{3}, \pm \frac{{2\pi }}{3}, \ldots}$$

بنابراین، تابع، تنها در نقطه $$\theta = 0$$ از بازه $$\left( { – {\large\frac{\pi }{4}\normalsize},{\large\frac{\pi }{4}\normalsize}} \right)$$ تعریف نشده است. مشتق در این نقطه، بی‌نهایت و خط مماس بر منحنی، عمودی است.

مثال ۶: مارپیچ گالیله

مشتق مارپیچ گالیله را محاسبه کنید.

حل: مارپیچ گالیله، مسیر جسمی را توصیف می‌کند که آزادانه در دستگاه مختصات در حالِ چرخشِ زمین سقوط می‌کند.

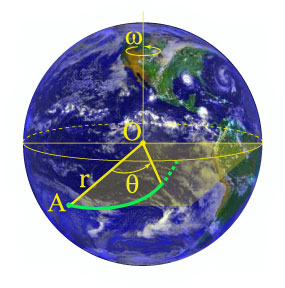
ابتدا معادله منحنی را در مختصات قطبی می‌نویسیم. فرض کنید جسمی از نقطه $$A$$ روی خط استوا، سقوط می‌کند. حرکت در امتداد شعاع بردار $$r$$ به‌صورت یکنواخت شتاب یافته و با رابطه زیر بیان می‌شود:

$$r = H + R – \frac{{g{t^2}}}{2}$$

که در آن، $$H$$ ارتفاع اولیه جسم از سطح زمین، $$R$$ شعاع زمین، $$g$$ شتاب گرانشی و $$t$$ زمان است.

هم‌زمان با سقوط جسم، زمین با سرعت زاویه‌ای ثابت $$\omega$$ می‌چرخد. زاویه $$\theta$$ که با زمان تغییر می‌کند، به‌صورت زیر تعریف می‌شود:

$$\theta = \omega t = \frac{{2\pi }}{T}t$$

که در آن، $$\omega$$ سرعت زاویه‌ای چرخش زمین و $$T$$ دوره تناوب چرخش است ($$T = 24\;\text{hours} = 86,400\;\text{sec}$$).

در نتیجه، معادلات پارامتری منحنی به‌فرم زیر هستند:

$$\left\{ \begin{array}{l}
r = H + R – \frac{{g{t^2}}}{2}\\
\theta = \frac{{2\pi }}{T}t
\end{array} \right.$$

اگر پارامتر $$t$$ را حذف کنیم، معادله قطبی مسیر به‌دست می‌آید:

$${t = \frac{T}{{2\pi }}\theta ,\;\;}\Rightarrow
{r = H + R – \frac{g}{2}{\left( {\frac{T}{{2\pi }}\theta } \right)^2} }
= {H + R – \frac{{g{T^2}}}{{8{\pi ^2}}}{\theta ^2}.}$$

معادله فوق را می‌توان به‌شکل زیر نوشت:

$${r\left( \theta \right) = a{\theta ^2} – d,\;\;}\kern-0.3pt
$$

که در آن،

$${a = – \frac{{g{T^2}}}{{8{\pi ^2}}},\;\;}\kern-0.0pt
{d = – \left( {H + R} \right).}$$

معادله اخیر را معادله قطبی مارپیچ گالیله می‌نامند. در مدل ما، یک دور مارپیچ، معادل یک تحویل یا دور زمین است. اگر متغیر  یا جمله $$a{\theta ^2}$$ را در نظر بگیریم ($$d = 0$$)، معادله مارپیچ به‌صورت زیر خواهد بود:

$$r = f\left( \theta \right) = a{\theta ^2}$$

همان‌گونه که از شکل زیر مشخص است، مارپیچ گالیله، شبیه مارپیچ ارشمیدس است، اما طول مارپیچ گالیله، سریع‌تر از مارپیچ ارشمیدس افزایش می‌یابد (به‌دلیل توان دوم زاویه).

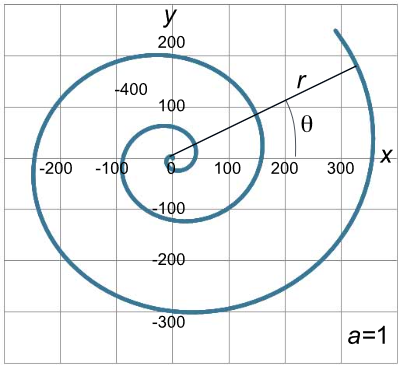
مشتق تابع قطبی بالا به‌صورت زیر است:‌

$${r’\left( \theta \right) = f’\left( \theta \right) }
= {{\left( {a{\theta ^2}} \right)^\prime } = 2a\theta .}$$

با جایگذاری رابطه اخیر در فرمول $$\large\frac{{dy}}{{dx}}\normalsize$$، داریم:

$${\frac{{dy}}{{dx}} = {y’_x} = \frac{{{y’_\theta }}}{{{x’_\theta }}} }\\
= {\frac{{f’\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f’\left( \theta \right)\cos\theta – f\left( \theta \right)\sin\theta }} }
= {\frac{{2a\theta \sin \theta + a{\theta ^2}\cos\theta }}{{2a\theta \cos\theta – a{\theta ^2}\sin\theta }} }\\
= {\frac{{{a\theta} \left( {2\sin \theta + \theta \cos\theta } \right)}}{{ {a\theta} \left( {2\cos\theta – \theta \sin\theta } \right)}} }\\
= {\frac{{2\tan\theta + \theta }}{{2 – \theta \tan \theta }} }
= {\frac{{2\tan\theta + 2 \cdot \frac{\theta }{2}}}{{2 – 2 \cdot \frac{\theta }{2} \cdot \tan \theta }} }\\
= {\frac{{{2}\left( {\tan\theta + \frac{\theta }{2}} \right)}}{{{2}\left( {1 – \tan \theta \cdot \frac{\theta }{2}} \right)}} }
= {\frac{{\tan\theta + \frac{\theta }{2}}}{{1 – \tan \theta \cdot \frac{\theta }{2}}}.}$$

مانند مثال ۱، زاویه $${\large\frac{\theta }{2}\normalsize}$$ را به‌فرم زیر نمایش می‌دهیم:

$${\frac{\theta }{2} }={ \tan \left( {\arctan \frac{\theta }{2}} \right)}$$

همچنین از اتحاد زیر استفاده می‌کنیم:

$${\tan \left( {\alpha + \beta } \right) }={ \frac{{\tan \alpha + \tan \beta }}{{1 – \tan \alpha \cdot \tan \beta }}.}$$

در نتیجه، مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$‌ مارپیچ گالیله را می‌توانیم به‌صورت زیر بنویسیم:

$${\frac{{dy}}{{dx}} = \frac{{\tan \theta + \frac{\theta }{2}}}{{1 – \tan \theta \cdot \frac{\theta }{2}}} }
= {\frac{{\tan \theta + \tan \left( {\arctan \frac{\theta }{2}} \right)}}{{1 – \tan \theta \cdot \tan \left( {\arctan \frac{\theta }{2}} \right)}} }\\
= {\tan \left( {\theta + \arctan \frac{\theta }{2}} \right).}$$

مثال ۷: مارپیچ فرما

مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$ مارپیچ فِرما را محاسبه کنید:

$$r = \sqrt \theta$$

حل: در مارپیچ فرما، شعاع $$r$$ با ریشه دوم زاویه $$\theta$$ متناسب است و به همین دلیل، به‌آرامی تغییر می‌کند. همان‌گونه که در شکل زیر نشان داده شده است، تراکم دورها، به‌اندازه $$r$$ افزایش می‌یابد.

مارپیچ فرما را می‌توان به شکل‌های مختلف در طبیعت پیدا کرد. برای مثال، آرایش دانه‌های آفتاب‌گردان، شبیه مارپیچ فرما است.

برای محاسبه مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$، ابتدا $$f’\left( \theta \right)$$ را در مختصات قطبی محاسبه می‌کنیم:

$${r’\left( \theta \right) = f’\left( \theta \right) }={ \frac{1}{{2\sqrt \theta }}.}$$

در نتیجه، مشتق در مختصات کارتزین را می‌توان به‌صورت زیر به‌دست آورد:

$${\frac{{dy}}{{dx}} = {y’_x} = \frac{{{y’_\theta }}}{{{x’_\theta }}} }\\
= {\frac{{f’\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f’\left( \theta \right)\cos\theta – f\left( \theta \right)\sin\theta }} }
= {\frac{{2a\theta \sin \theta + a{\theta ^2}\cos\theta }}{{2a\theta \cos\theta – a{\theta ^2}\sin\theta }} }\\
= {\frac{{{a\theta} \left( {2\sin \theta + \theta \cos\theta } \right)}}{{{a\theta} \left( {2\cos\theta – \theta \sin\theta } \right)}} }\\
= {\frac{{2\tan\theta + \theta }}{{2 – \theta \tan \theta }} }
= {\frac{{2\tan\theta + 2 \cdot \frac{\theta }{2}}}{{2 – 2 \cdot \frac{\theta }{2} \cdot \tan \theta }} }\\
= {\frac{{\cancel{2}\left( {\tan\theta + \frac{\theta }{2}} \right)}}{{\cancel{2}\left( {1 – \tan \theta \cdot \frac{\theta }{2}} \right)}} }
= {\frac{{\tan\theta + \frac{\theta }{2}}}{{1 – \tan \theta \cdot \frac{\theta }{2}}}.}$$

می‌توانیم عبارت بالا را نوشتن عبارت $$2\theta$$ ساده‌تر کنیم:

$$2\theta = \tan\left( {\arctan 2\theta } \right)$$

همچنین، اتحاد زیر را به‌کار می‌گیریم:

$${\tan \left( {\alpha + \beta } \right) }={ \frac{{\tan \alpha + \tan \beta }}{{1 – \tan \alpha \cdot \tan \beta }}.}$$

در نهایت، مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$ به‌شکل زیر به‌دست می‌آید:

$${\frac{{dy}}{{dx}} = \frac{{\tan \theta + 2\theta }}{{1 – 2\theta \tan \theta }} } \\
= {\frac{{\tan \theta + \tan \left( {\arctan 2\theta } \right)}}{{1 – \tan \theta \cdot \tan \left( {\arctan 2\theta } \right)}} }
= {\tan \left( {\theta + \arctan 2\theta } \right).}$$

اگر این مطلب برای شما مفید بوده است و علاقه‌مند به یادگیری بیشتر در این زمینه هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• تقلب نامه (Cheat Sheet) مفاهیم و روابط مشتق
• مشتق توابع هذلولوی و معکوس آن‌ها — از صفر تا صد
• مشتق توابع معکوس مثلثاتی — به زبان ساده

^^