چگونه مساحت مثلث مختلف الاضلاع را حساب کنیم؟ + حل تمرین و مثال

مساحت مثلث مختلف الاضلاع، معمولا با استفاده از فرمول کلی (قاعده ضرب در ارتفاع تقسیم بر دو)، فرمول هرون و روابط مثلثاتی محاسبه میشود. البته روشهای دیگری نظیر دترمینان مختصات راسها و ضرب برداری ضلعها نیز برای تعیین مساحت این شکل هندسی مورد استفاده قرار میگیرند. در این آموزش، به معرفی روشهای اصلی محاسبه مساحت مثلث مختلف الاضلاع نظیر قاعده و ارتفاع، هرون و مثلثات به همراه چند مثال میپردازیم. در انتها نیز، جدول خلاصه فرمولهای مساحت این نوع مثلث را ارائه میکنیم.
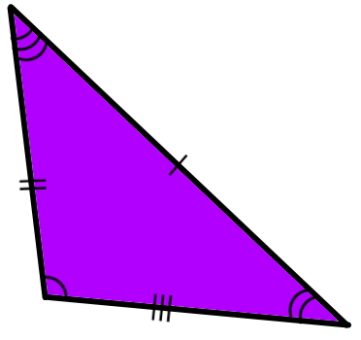
مثلث مختلف الاضلاع چیست ؟
مثلث مختلف الاضلاع (به انگلیسی Scalene Triangle)، یکی از انواع مثلث است که اندازه تمام ضلعها و زوایای آن با یکدیگر تفاوت دارد. بر اساس این تعریف، مثلثهای متساوی الاضلاع و متساوی الساقین، به عنوان مثلث مختلف الاضلاع در نظر گرفته نمیشوند. با این وجود، برخی از مثلثهای قائم الزاویه میتوانند در گروه مثلثهای مختلف الاضلاع قرار بگیرند.
مساحت مثلث مختلف اضلاع چیست ؟
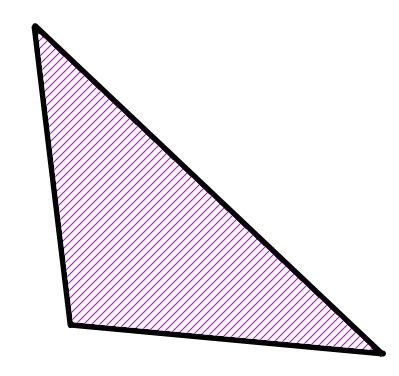
مساحت مثلث مختلف اضلاع و دیگر شکلهای هندسی، اندازه سطح درون ضلعهای این شکلها است.
به عنوان مثال، ناحیه هاشور خورده در تصویر زیر، مساحت یک مثلث مختلف اضلاع را نمایش میدهد.
مساحت مثلث مختلف الاضلاع چگونه بدست می آید ؟
مساحت مثلث مختلف اضلاع و دیگر انواع مثلثها، معمولا از ضرب قاعده در ارتفاع تقسیم بر دو به دست میآید.
در تصویر زیر، هر یک از قاعدهها و ارتفاعهای نظیر یک مثلث مختلف الاضلاع با رنگهای یکسان نشان داده شدهاند.
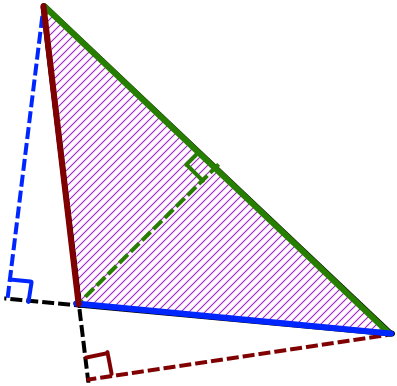
فرمول مساحت مثلث مختلف الاضلاع با ارتفاع و قاعده به صورت زیر نوشته میشود:
- A: مساحت (ناحیه هاشور خورده)
- b: یکی از قاعدههای مثلث (اندازه یکی از ضلعها)
- h: ارتفاع نظیر قاعده b (اندازه خط چین هم رنگ با قاعده)
هر فرمولی که برای محاسبه مساحت مثلث مختلف الاضلاع قابل استفاده باشد، برای تمامی انواع مثلثها قابل استفاده خواهد بود.
مثال: محاسبه مساحت مثلث مختلف اضلاع با ارتفاع و قاعده
مثلث مختلف الاضلاع زیر را در نظر بگیرید. مساحت این مثلث چقدر است؟
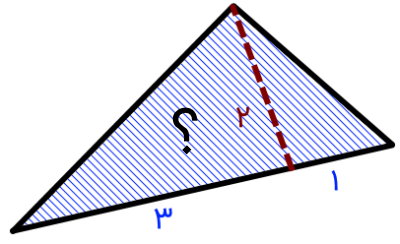
برای شروع حل مسئله، فرمول مساحت مثلث با ارتفاع و قاعده را مینویسیم:
- A: مساحت
- b: قاعده مثلث برابر جمع دو بخش با اندازههای 1 و 3
- h: ارتفاع مثلث برابر 2
اندازههای داده شده را در فرمول قرار میدهیم:
مساحت مثلث برابر 4 است. یکا یا واحد مساحت، به یکای اندازههای داده شده بستگی دارد. به عنوان مثال، اگر واحد ارتفاع و قاعده، سانتیمتر بود، مساحت مثلث با واحد سانتیتر مربع (مانند 4 سانتیمتر مربع) بیان میشد.
مساحت مثلث مختلف الاضلاع با سه ضلع چگونه بدست می آید ؟
مساحت مثلث مختلف الاضلاع با سه ضلع، توسط فرمول هرون به دست میآید. مثلث مختلف الاضلاع زیر را در نظر بگیرید.
فرمول هرون، به عنوان یک روش کلی برای تعیین مساحت تمام مثلثها، به صورت زیر نوشته میشود:
با توجه به مثلث نمایش داده شده در تصویر بالا، داریم:
- A: مساحت (ناحیه رنگی)
- s: نصف محیط مثلث (نصف مجموع اندازه تمام ضلعها)
- a: اندازه ضلع a
- b: اندازه ضلع b
- c: اندازه ضلع c
مثال: محاسبه مساحت مثلث مختلف الاضلاع بدون ارتفاع
مثلثی با ضلعهایی به اندازه 3، 4 و 5 را در نظر بگیرید. مساحت این مثلث را بدون ارتفاع محاسبه کنید.
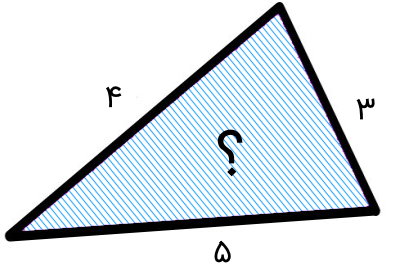
به دلیل مشخص بودن طول هر سه ضلع مثلث، برای محاسبه مساحت آن، نیازی به دانستن ارتفاع و قاعده نداریم. از اینرو، ابتدا فرمول هرون را مینویسیم:
- A: مساحت (ناحیه هاشور)
- s: نصف محیط مثلث
- a: ضلع با اندازه 3
- b: ضلع با اندازه 4
- c: ضلع با اندازه 5
نصف محیط مثلث بالا از رابطه زیر به دست میآید:
اکنون، تمام اندازه و مقادیر به دست آمده را درون فرمول قرار میدهیم:
مساحت مثلث مختلف الاضلاع با ضلعهای 3، 4 و 5، برابر 6 است.
مساحت مثلث مختلف الاضلاع با سینوس
یکی دیگر از روشهای پرکاربرد برای محاسبه مساحت مثلثهای مختلف الاضلاع، استفاده از روابط مثلثاتی، قانون سینوسها و مقدار سینوسها است.
اگر اندازه برخی از ضلعها و زوایای مثلث مشخص باشند، امکان استفاده از این روش فراهم میشود. مثلث زیر را در نظر بگیرید.
مساحت مثلث مختلف الاضلاع با دو ضلع و زاویه بین
در حالت مشخص بودن دو ضلع و زاویه بین، فرمولهای مساحت مثلث مختلف الاضلاع با روابط مثلثاتی به صورت زیر خواهند بود:
- Area: مساحت
- a: طول ضلع BC
- b: طول ضلع AC
- c: طول ضلع AB
- A: زاویه راس A
- B: زاویه راس B
- C: زاویه راس C
مساحت مثلث مختلف الاضلاع با دو زاویه و ضلع بین
اگر دو زاویه و ضلع بین آنها در یک مثلث مختلف الاضلاع مشخص باشد، مساحت آن با استفاده از فرمولهای زیر محاسبه میشود:
- Area: مساحت
- a: طول ضلع BC
- b: طول ضلع AC
- c: طول ضلع AB
- A: زاویه راس A
- B: زاویه راس B
- C: زاویه راس C
نکته: در کسر فرمولهای بالا به جای جمع دو زاویه، میتوانیم از زاویه سوم استفاده کنیم. این زاویه از قانون جمع زوایای داخلی، به دست میآید.
مثال: محاسبه مساحت با سینوس
در مثلث زیر، اندازه تمام ضلعها و زوایا داده شده است. مساحت مثلث را به دو روش مثلثاتی به دست بیاورید.
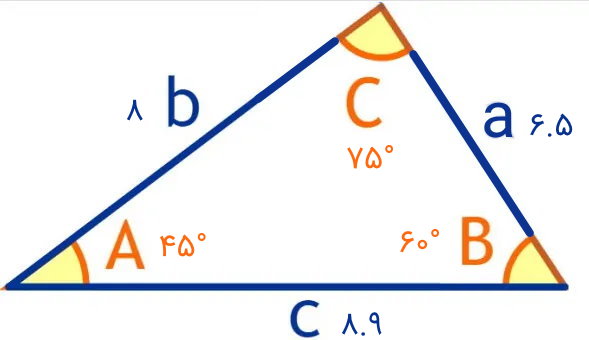
به دلیل مشخص بودن تمام زوایا و ضلعهای مثلث، میتوانیم از فرمولهای دو ضلع و زاویه بین یا دو زاویه و ضلع بین استفاده کنیم. برای شروع، ضلع a و b را به همراه زاویه C در نظر میگیریم. فرمول مساحت مثلث با سینوس در این حالت به صورت زیر نوشته میشود:
- Area: مساحت
- a: اندازه ضلع a برابر 6.5
- b: اندازه ضلع b برابر ۸
- C: اندازه زاویه C برابر 75 درجه
اندازههای داده شده را درون فرمول قرار میدهیم:
روش دوم، استفاده از فرمول مساحت مثلث با دو زاویه و ضلع بین است. در اینجا، زاویه A، زاویه B و ضلع c را در نظر میگیریم و فرمول مخصوص این حالت را مینویسیم:
- Area: مساحت
- c: اندازه ضلع c برابر 8.9
- A: اندازه زاویه A برابر 45 درجه
- B: اندازه زاویه B برابر 60 درجه
اندازههای داده شده را درون فرمول قرار میدهیم:

مثال های محاسبه مساحت مثلث مختلف الاضلاع
در این بخش، به تشریح چهار مثال در زمینه محاسبه مساحت مثلثهای مختلف اضلاع میپردازیم.
مثال اول: تعیین مساحت از روی قاعده و ارتفاع
اگر اندازه یکی از ضلعهای مثلثی برابر 9 سانتیمتر و اندازه ارتفاع نظیر آن ضلع برابر 3 سانتیمتر باشد، مساحت مثلث چقدر است؟
در صورت دانستن اندازه ارتفاع و قاعده، از فرمول کلی مساحت مثلث استفاده میکنیم:
2 ÷ ارتفاع قاعده = مساحت مثلث
مساحت مثلث برابر 13.5 سانتیمتر مربع است.
مثال دوم: محاسبه ارتفاع مثلث مختلف الاضلاع
مثلثی با مساحت 27 سانتیمتر مربع با ضلعهای 18، 12 و 30 سانتیمتر را در نظر بگیرید. اندازه یکی از ارتفاعهای این مثلث را محاسبه کنید.
بر اساس رابطه کلی مساحت مثلثها، داریم:
2 ÷ قاعده ارتفاع = مساحت مثلث
- A: مساحت (27 سانتیمتر مربع)
- b: اندازه یکی از ضلعهای مثلث (18، 12 یا 30 سانتیمتر)
- h: ارتفاع نظیر قاعده
از بین اندازه ضلعهای داده شده، یکی را داخل فرمول بالا قرار میدهیم (به عنوان مثال، از ضلع 12 سانتیمتری استفاده میکنیم):
در نتیجه، ارتفاع نظیر ضلع 12 سانتیمتری برابر 4.5 سانتیمتر است. اگر به جای این ضلع، ضلع 18 سانتیمتری را در رابطه بالا قرار میدادیم، ارتفاع نظیر آن به صورت زیر مشخص میشد:
بنابراین، در این مثال، ارتفاع نظیر ضلع 18 سانتیمتری برابر 3 سانتیمتر است. ارتفاع ضلع سوم نیز به همین صورت قابل محاسبه خواهد بود.

مثال سوم: مساحت مثلث با سه ضلع
مساحت مثلثی با ضلعهای 5، 12 و 13 را محاسبه کنید.
در این مسئله، هیچ یک از ارتفاعهای مثلث داده نشدهاند. به همین دلیل، امکان محاسبه مساحت با استفاده از روش قبلی وجود ندارد. در عوض، به دلیل مشخص بودن اندازه تمام ضلعهای مثلث، فرمول هرون، بهترین گزینه برای حل مسئله است. این فرمول به صورت زیر نوشته میشود:
- A: مساحت
- s: نصف محیط
- a: ضلع با اندازه 5
- b: ضلع با اندازه 12
- c: ضلع با اندازه 13
نکته: در فرمول بالا، اهمیتی ندارد که کدام اندازه را برای کدام علامت (b ،a یا c) در نظر میگیرد.
پیش از قرار دادن اندازههای داده شده در فرمول، نصف محیط را به دست میآوریم:
عدد بالا را به همراه دیگر اندازهها، درون فرمول هرون قرار میدهیم:
مساحت مثلث برابر 30 است.
مثال چهارم: مساحت مثلث با دو ضلع و زاویه غیر بین
مساحت مثلث مختلف الاضلاع زیر را با استفاده از روابط مثلثاتی به دست بیاورید.
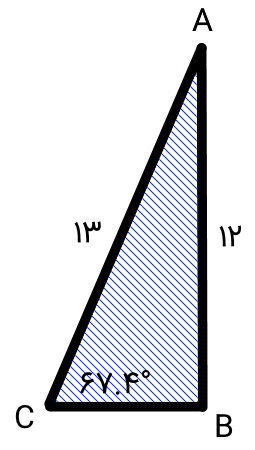
پیش از نوشتن فرمولها، ابتدا اطلاعات مسئله را یادداشت میکنیم:
- AB = 12
- AC = 13
- C= 67.4°
در این مثلث، طول دو ضلع و زاویه غیر بین آنها داده شده است. از اینرو، ابتدا باید با استفاده از قانون سینوسها، اطلاعات بیشتری از زاویههای دیگر به دست بیاوریم. قانون سینوسها عبارت است از:
اندازههای داده شده را در نسبتهای بالا قرار میدهیم:
به دلیل 1 بودن سینوس زاویه B، مقدار این زاویه برابر 90 درجه بوده و مثلث مورد بررسی، قائم الزاویه است. با توجه به قانون جمع زوایای داخلی، زاویه C برابر 22.6 درجه خواهد بود. اکنون میتوانیم از فرمولهای دو ضلع و زاویه بین یا دو زاویه ضلع بین استفاده کنیم. به عنوان مثال، فرمول مساحت مثلث با دو زاویه و ضلع بین را برای زاویه A، ضلع AB و زاویه B مینویسیم:
مساحت مثلث برابر 30 است. البته به دلیل قائم الزاویه بودن این مثلث، فرمول سادهتری برای حل این مسئله وجود داشتند که در مطلب «فرمول مساحت مثلث — روشهای محاسبه مساحت مثلث» و جدول بخش بعدی به معرفی آن پرداختهایم.
جدول فرمول های مساحت مثلث مختلف الاضلاع
جدول زیر، تمام فرمولهای معرفی شده در این مقاله را به صورت خلاصه نمایش میدهد.
| اندازههای موجود | فرمول مساحت مثلث مختلف الاضلاع |
| قاعده و ارتفاع |
قاعده ضربدر ارتفاع تقسیم بر دو
|
| سه ضلع | |
| دو ضلع و زاویه بین | |
| دو زاویه و ضلع بین | |
| یک ضلع و وتر
(مثلث مختلف الاضلاع قائم الزاویه) |
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مثلث — انواع مثلث و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مثلث چیست ؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)
- مساحت انواع مثلث چگونه بدست می آید ؟ — حل تمرین و مثال های متنوع
- محیط مثلث چگونه بدست می آید؟ + فیلم آموزش رایگان
- چگونه مساحت مثلث را حساب کنیم؟ + فیلم آموزشی و تمرین با جواب
- محاسبه آنلاین مساحت مثلث — معرفی بهترین سایتها + مثال
- فرمول محیط مثلث چیست ؟ انواع فرمول ها + حل مثال های متنوع
- فرمول مساحت مثلث چیست ؟ — تمام فرمول ها + حل تمرین
- قاعده مثلث چیست و چگونه بدست می آید ؟ + تعریف و مثال
- ارتفاع مثلث چیست و چگونه رسم می شود ؟ — آموزش تصویری + حل تمرین
- محاسبه ارتفاع مثلث — تعریف، حل تمرین و مثال + جدول فرمول ها
- محیط مثلث مختلف الاضلاع — به زبان ساده + حل مثال های متنوع
- چگونه مساحت مثلث مختلف الاضلاع را حساب کنیم؟ + حل تمرین و مثال(همین مطلب)
- چگونه مساحت مثلث با سه ضلع معلوم را حساب کنیم؟ + حل تمرین و مثال
- فرمول هرون — به زبان ساده
- مساحت مثلث با سینوس چگونه محاسبه می شود ؟ + حل تمرین و جدول فرمول ها
- مثلث قائم الزاویه چیست ؟ — تعریف، ویژگی ها و محاسبات | به زبان ساده
- محیط مثلث قائم الزاویه — به زبان ساده + حل مثال های متنوع
- مساحت مثلث قائم الزاویه — حل تمرین و مثال های متنوع
- مثلث متساوی الساقین چیست ؟ | تعریف، ویژگی ها و محاسبات — به زبان ساده
- محیط مثلث متساوی الساقین — به زبان ساده و با حل مثال
- مساحت مثلث متساوی الساقین — حل تمرین و مثال های متنوع
- محیط مثلث متساوی الاضلاع چگونه بدست می آید؟ + حل مثال و تمرین
- مساحت مثلث متساوی الاضلاع — حل تمرین و مثال های متنوع












