مساحت لوزی با قطر چگونه بدست می آید؟ — به زبان ساده + حل تمرین و مثال

مساحت لوزی با قطر عبارت از «حاصلضرب قطر بزرگ در قطر کوچک تقسیم بر 2» است. در صورت مشخص بودن اندازه قطر و یکی از ضلعهای لوزی، امکان محاسبه مساحت با یک فرمول مخصوص نیز وجود دارد. در این آموزش، به معرفی فرمولها، نحوه محاسبه و اثبات مساحت لوزی با قطر به همراه حل چند مثال متنوع میپردازیم.
مساحت لوزی چیست؟
مساحت لوزی، اندازه سطحی است که درون ضلعهای این چهارضلعی قرار میگیرد. به عنوان مثال، بخش رنگی شکل زیر، مساحت یک لوزی را نمایش میدهد.

قطر لوزی چیست؟
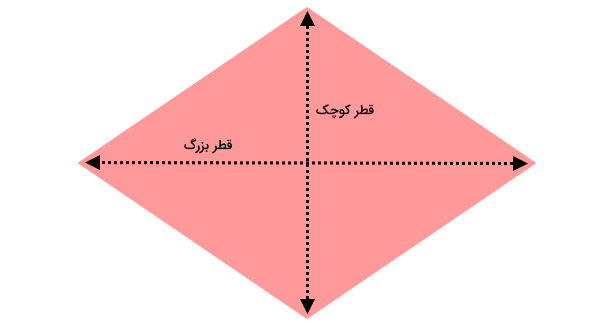
قطر لوزی، فاصله بین دو گوشه روبهرویی (راسهای غیر مجاور) است. لوزی، دو قطر عمود بر هم دارد. به دلیل متفاوت بودن اندازه این قطرها، به آنها قطر بزرگ و قطر کوچک میگویند.
اندازه قطر کوچک و بزرگ لوزی، به منظور محاسبه مساحت این شکل هندسی مورد استفاده قرار میگیرد. البته این اندازهها در محاسبه محیط لوزی نیز کاربرد دارند.
نکته: مربع، یک حالت خاص لوزی، با قطرهای برابر است.
مساحت لوزی با قطر چگونه بدست می آید؟
متداولترین روش برای محاسبه مساحت لوزی، استفاده از اندازه قطرهای آن است. مساحت لوزی از تقسیم حاصلضرب دو قطر آن بر عدد ۲ به دست میآید. رابطه کلامی یا فرمول مساحت لوزی به زبان فارسی به صورت زیر نوشته میشود:
۲ ÷ (قطر کوچک × قطر بزرگ) = مساحت لوزی
مثال ۱: محاسبه مساحت لوزی با قطر
مساحت شکلهای زیر را به دست بیاورید. مساحتهای به دست آمده را با هم مقایسه کنید.
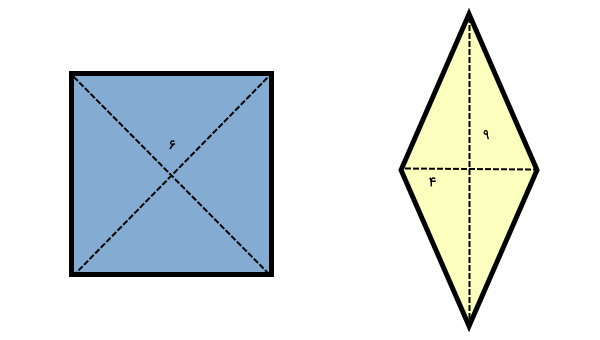
تصویر بالا، شکل یک مربع به قطر ۶ و یک لوزی به قطرهای ۹ و ۴ را نمایش میدهد. مساحت لوزی از فرمول زیر به دست میآید:
۲ ÷ (قطر کوچک × قطر بزرگ) = مساحت لوزی
اندازههای معلوم (قطر بزرگ و کوچک) را درون رابطه بالا قرار میدهیم:
۲ ÷ (۴ × ۹) = مساحت لوزی
۲ ÷ (۳۶) = مساحت لوزی
۱۸ = مساحت لوزی
اکنون باید مساحت مربع را حساب کنیم. فرمول اصلی مساحت مربع برابر «اندازه یک ضلع ضربدر خودش» است. بر اساس اطلاعات مسئله، اندازه ضلع مربع را نداریم. با این وجود، اندازه قطر آن داده شده است. مربع، یک نوع لوزی محسوب میشود. بنابراین، میتوانیم مساحت آن را نیز به کمک فرمول مساحت قطر به دست بیاوریم:
۲ ÷ (قطر کوچک × قطر بزرگ) = مساحت مربع
توجه داشته باشید که اندازه هر دو قطر مربع برابر هستند. از اینرو، به جای قطر کوچک و قطر بزرگ، یک اندازه را قرار میدهیم:
۲ ÷ (۶ × ۶) = مساحت مربع
۲ ÷ (۳۶) = مساحت مربع
۱۸ = مساحت مربع
در نتیجه مساحت مربع نیز برابر با ۱۸ است. با مقایسه اندازه مساحت لوزی و مربع در این مثال میتوانیم نتیجه بگیریم که دو لوزی با قطرهای متفاوت میتوانند مساحتهای برابر داشته باشند.
قطرهای لوزی، برای تعیین محیط آن نیز به کار برده میشوند. به منظور آشنایی با این کاربرد، پیشنهاد میکنیم مطالب زیر را مطالعه کنید:
- محیط لوزی چگونه بدست میآید؟ — فیلم آموزش رایگان + حل مثال
- فرمول محیط لوزی چیست؟ — به زبان ساده + حل تمرین و مثال
مساحت لوزی با قطر به صورت جبری
عبارت جبری مساحت لوزی با قطر به صورت زیر نوشته میشود:
- A: مساحت لوزی
- p: قطر بزرگ لوزی
- q: قطر کوچک لوزی
مثال ۲: محاسبه مساحت لوزی با عبارت جبری
مساحت لوزی به قطر بزرگ ۱۷ سانتیمتر و قطر کوچک ۱۵ سانتیمتر را حساب کنید.
برای حل این مسئله، فرمول مساحت لوزی با قطر را مینویسیم:
- A: مساحت لوزی
- p: قطر بزرگ لوزی برابر ۱۷ سانتیمتر
- q: قطر کوچک لوزی برابر ۱۵ سانتیمتر
در نتیجه، مساحت لوزی برابر ۱۲۷/۵ سانتیمتر مربع است. در صورت تمایل به مشاهده مثالهای بیشتر، مطالعه مطلب «مسئله در مورد مساحت لوزی با جواب — حل سوالات امتحانی» را به شما پیشنهاد میکنیم.
مساحت لوزی با یک قطر و ضلع
در صورتی که اندازه ضلع لوزی و اندازه یکی از قطرهای آن مشخص باشد، مساحت لوزی با استفاده از فرمول زیر محاسبه میشود:
- A: مساحت لوزی
- p: یکی از قطرهای لوزی
- a: ضلع لوزی
این فرمول، یکی از فرمولهای محاسبه مساحت لوزیها بدون قطر است که با قضیه فیثاغورس اثبات میشود.
مثال ۳: محاسبه مساحت لوزی با ضلع و قطر
مساحت لوزی زیر را به دست بیاورید.
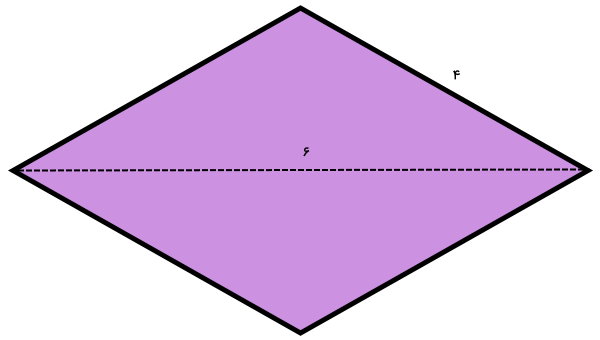
در تصویر بالا، اندازه یکی از قطرها و ضلعهای لوزی داده شده است. با توجه به اطلاعات موجود، مساحت لوزی با استفاده از فرمول زیر محاسبه میشود:
- A: مساحت لوزی
- p: یکی از قطرهای لوزی برابر 6
- a: ضلع لوزی برابر 3
در نتیجه، مساحت لوزی برابر ۱۵/۸۷ است.
اثبات فرمول مساحت لوزی با قطر و ضلع
در بخشهای قبل، اشاره کردیم که فرمول مساحت لوزی با ضلع و قطر، توسط قضیه فیثاغورس به دست میآید. بر اساس این قضیه، مجموع مربعات ساقهای یک مثلث قائم الزاویه با مربع وتر آن برابر است. لوزی زیر را به همراه قطرهای آن در نظر بگیرید.
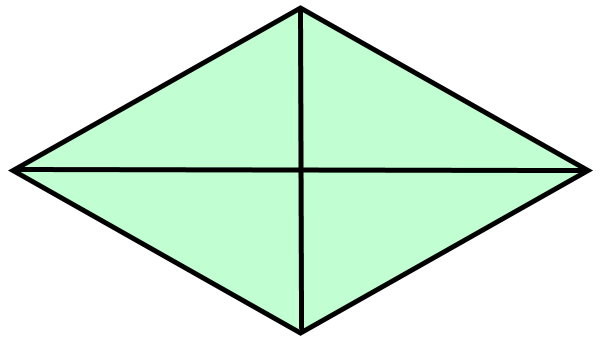
قطرهای لوزی بالا، آن را به چهار مثلث تقسیم کردهاند. ضلعهای لوزی با یکدیگر برابر بوده و قطرهای آن، عمود منصف یکدیگر هستند. بنابراین، میتوانیم اندازههای مثلثهای بالا را به صورت زیر مشخص کنیم.
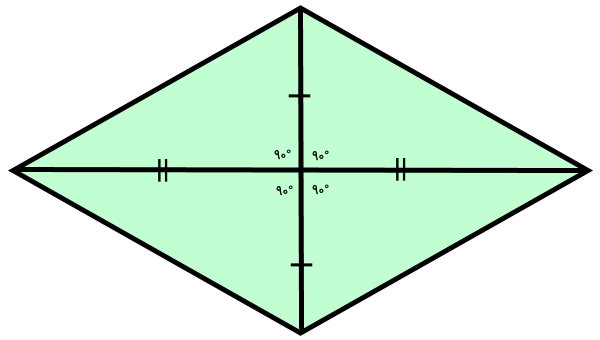
بر اساس حالت همنهشتی دو ضلع و زاویه بین (ض ز ض)، هر چهار مثلث بالا با یکدیگر برابرند. مساحت لوزی برابر مجموع مساحتهای این مثلثها است:
مثلث + مثلث + مثلث + مثلث = مساحت لوزی
مثلث × ۴ = مساحت لوزی
به این ترتیب، اگر اندازه مساحت یکی از مثلثها را داشته باشیم، امکان محاسبه مساحت لوزی فراهم میشود. مثلثهای بالا، قائم الزاویهاند. ضلع لوزی، به عنوان وتر و نصف قطرهای لوزی به عنوان ساقهای هر مثلث در نظر گرفته میشوند.
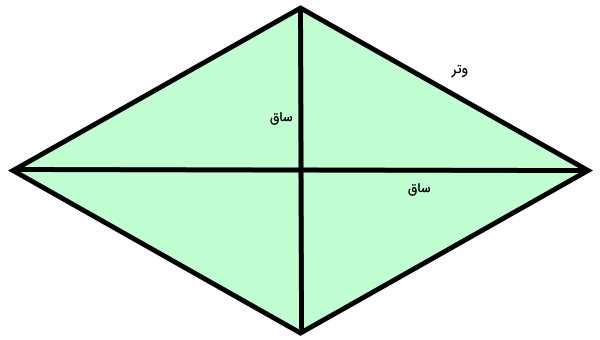
قضیه فیثاغورس برای هر مثلث عبارت است از:
- c: ضلع لوزی (وتر مثلث)
- a: نصف قطر بزرگ لوزی (یکی از ساقها)
- b: نصف قطر کوچک لوزی (ساق دیگر)
اگر قطرهای لوزی را برابر p و q در نظر بگیریم، خواهیم داشت:
بر اساس رابطه بالا، با مشخص بودن اندازه ضلع لوزی و یکی از قطرهای لوزی، امکان محاسبه اندازه قطر دیگر فراهم میشود:
مطابق با فرمول مساحت لوزی با قطر، داریم:
- A: مساحت لوزی
- p: یکی از قطرهای لوزی
- q: قطر دیگر لوزی
به جای p، خودش را قرار داده و به جای q، رابطه بدست آمده از قضیه فیثاغورس را قرار میدهیم:
فرمول بالا، همان فرمول مساحت لوزی با ضلع و قطر است.
سوالات متداول در رابطه با مساحت لوزی با قطر
در این بخش، به برخی از سوالات پرتکرار در رابطه با مساحت لوزی با قطر به طور خلاصه پاسخ میدهیم.
مساحت لوزی با قطر چیست ؟
مساحت لوزی با قطر، حاصلضرب قطرها تقسیم بر دو است.
فرمول مساحت لوزی با قطر چگونه نوشته میشود؟
فرمول مساحت لوزی با قطر به صورت A=(pq)÷2 نوشته میشود.
آیا امکان محاسبه مساحت لوزی با یک قطر وجود دارد؟
بله. در صورت مشخص بودن یک ضلع و یک قطر، امکان محاسبه مساحت لوزی وجود خواهد داشت.
فرمول مساحت لوزی با ضلع چگونه نوشته میشود؟
فرمول مساحت لوزی با ضلع، توسط اندازه یکی از قطرها و قضیه فیثاغورس (بر حسب ضلع و قطر معلوم) نوشته میشود.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت لوزی — تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- لوزی و محاسبات آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- قطر لوزی چیست و چه ویژگی هایی دارد؟ — به زبان ساده + حل مثال
- محیط لوزی چگونه بدست می آید ؟ — فیلم آموزش رایگان + حل مثال
- مساحت لوزی چگونه بدست می آید ؟ — به زبان ساده + حل مثال
- فرمول محیط لوزی چیست ؟ — به زبان ساده + حل تمرین و مثال
- فرمول مساحت لوزی چیست ؟ — چهار فرمول + حل مثال های متنوع
- مسئله در مورد مساحت لوزی با جواب — حل سوالات امتحانی
- مساحت لوزی با قطر چگونه بدست می آید ؟ — به زبان ساده + حل تمرین و مثال(همین مطلب)
- مساحت لوزی بدون قطر چگونه بدست می آید ؟ — به زبان ساده + حل مثال
- مساحت لوزی داخل مستطیل چیست ؟ — به زبان ساده + حل مثال
- فرمول محاسبه قطر لوزی چیست ؟ — به زبان ساده + حل مثال
- نسبت ضلع به محیط لوزی چند است ؟ — به زبان ساده + حل مثال












