مدل پارامتر توزیع شده خط – از صفر تا صد

در آموزش‌های قبلی مجله فرادرس، مدل تکفاز، سه فاز و موج سیار خط انتقال را معرفی کردیم. در این آموزش، مدل حالت ماندگار یا مدل پارامتر توزیع شده خط را بررسی می‌کنیم. حالت ماندگار به این معنی است که ولتاژ‌ و جریان خط ماندگار بوده و با زمان تغییر نمی‌کنند.

مدل پارامتر توزیع شده خط تکفاز

شکل زیر مدل پارامتر توزیع شده تکفاز را نشان می‌دهد.

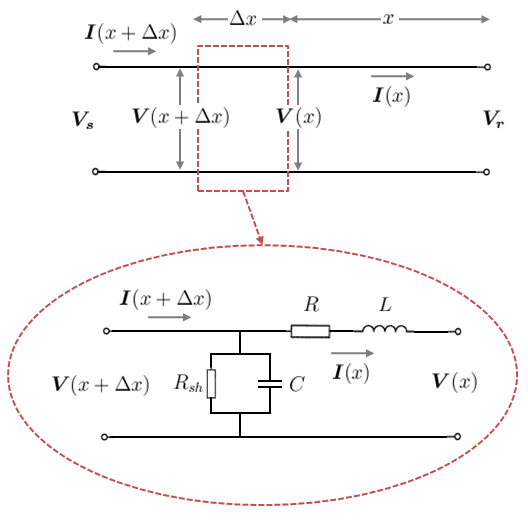
در یک خط انتقال واقعی، عناصر $$R$$، $$L$$ و $$C$$ مدار با یکدیگر تجمیع نیستند، اما به طور یکنواخت در در طول خط توزیع شده‌اند. برای توصیف طبیعت توزیع شده پارامترهای مدار، مدل خط تکفاز شکل ۱ را در نظر بگیرید. به طور خاص، یک بخش کوچک از خط را به طول $$\Delta x$$ متر در نظر بگیرید که در فاصله $$x$$ متری از باس دریافت قرار دارد.

نمودار بالایی شکل ۱ خط انتقال کامل و بخش کوچکی از خط را نشان می‌دهد که به دور آن خط‌چین رسم شده است. نمودار پایینی یک نمای دقیق‌تر از بخش مورد نظر خط است که یک مدل مرسوم با عناصر سری و موازی را برای بخشی از خط نشان می‌دهد. عناصر سری را می‌توان با یک امپدانس و عناصر موازی را با یک ادمیتانس به صورت زیر نمایش داد:

$$\large \boldsymbol { z } = R + j \omega L = R + j X \,$$

$$\large \boldsymbol { y } = \frac { 1 } { R _ { s h } } + j \omega C = G + j B \,$$

که در آن، $$R$$ مقاومت سری ($$\Omega /m$$)، $$X$$ راکتانس سری ($$\Omega /m$$)، $$G$$ رسانایی موازی ($$S /m$$) و $$B$$ سوسپتانس موازی ($$S /m$$) است.

لازم به ذکر است که مقادیر امپدانس و ادمیتانس برای هر متر بیان می‌‌شوند. بنابراین، امپدانس سری بخشی از خط به طول $$\Delta x$$ متر برابر با $$\boldsymbol{z} \Delta x \,$$ است. همین موضوع را می‌توان برای ادمیتانس شنت نیز بیان کرد.

استخراج معادلات ولتاژ و جریان

با تحلیل مدار با استفاده از KVL، می‌توان نوشت:

$$\large \boldsymbol { V } ( x + \Delta x ) = \boldsymbol { V } ( x ) + \boldsymbol { z } \Delta x \boldsymbol { I } ( x ) \,$$

اگر معادله بالا را بازنویسی کنیم، داریم:

$$\large \frac { \boldsymbol { V } ( x + \Delta x ) - \boldsymbol {V } ( x ) } { \Delta x } = \boldsymbol { z } \boldsymbol { I } ( x ) \,$$

معادله سمت چپ خارج قسمت تفاضلی نیوتن نامیده می‌شود و وقتی $$\Delta x \to 0$$، طبق تعریف برابر با مشتق $$\boldsymbol{V}(x)$$ است؛ یعنی:

$$\large \lim _ { \Delta x \to 0 } \frac { \boldsymbol { V } ( x + \Delta x ) - \boldsymbol { V } ( x ) } { \Delta x } = \frac { d \boldsymbol { V } ( x ) } { d x} = \boldsymbol { z } \boldsymbol { I } ( x ) \,$$

به طور مشابه، با تحلیل KCL مدار خواهیم داشت:

$$\large \boldsymbol { I } ( x + \Delta x ) = \boldsymbol { I } ( x ) + \boldsymbol { y } \Delta x \boldsymbol { V } ( x + \Delta x ) \,$$

اگر این معادله را بازنویسی کنیم، داریم:

$$\large \frac { \boldsymbol { I } ( x + \Delta x ) - \boldsymbol { I } ( x ) } { \Delta x } = \boldsymbol { y } \boldsymbol { V } ( x + \Delta x ) \,$$

حال حد $$\Delta x \to 0$$ را به دو طرف معادله بالا اعمال می‌کنیم که نتیجه آن به صورت زیر است:

$$\large \frac{d \boldsymbol{I}(x)}{dx} = \boldsymbol{y} \boldsymbol{V}(x) \, \; \; \; \; \; ( 2 )$$

با مشتق‌گیری از معادلات (۱) و (۲)، داریم:

$$\large \frac { d ^ { 2 } \boldsymbol { V } ( x) } { d x ^ { 2 } } = \boldsymbol { z } \frac { d \boldsymbol { I } ( x ) } { d x} \,$$

$$\large \frac { d ^ { 2 } \boldsymbol { I } ( x ) } { dx ^ { 2 } } = \boldsymbol { y } \frac { d \boldsymbol { V } ( x ) } { d x } \,$$

حال می‌توانیم معادلات بالا را به صورت زیر بنویسیم:

$$\large \frac { d ^ { 2 } \boldsymbol { V } ( x ) } { d x^ { 2 } } = \boldsymbol { z y } \boldsymbol { V } ( x ) \, \;\; \; \; \; ( 3 )$$

$$\large \frac { d ^ { 2} \boldsymbol { I } ( x ) } { d x ^ { 2 }} = \boldsymbol { z y } \boldsymbol { I } ( x ) \, \; \; \; \; \; ( 4 )$$

دو معادله بالا را می‌توان به فرم دستگاه معادلات خطی مرتبه دوم همگن نوشت:

$$\large \frac { d ^ { 2 } \boldsymbol { V } ( x )} { d x ^ { 2 } } - \boldsymbol { z y } \boldsymbol { V } ( x ) = 0 \,$$

جواب عمومی این معادله دیفرانسیل برابر است با:

$$\large \boldsymbol { V } ( x ) = A _ { 1 } e ^ { \boldsymbol { \gamma } x } + A _ { 2 } e ^ { - \boldsymbol { \gamma } x } \,$$

که در آن، $$\boldsymbol{\gamma} = \sqrt{\boldsymbol{zy}}$$ به عنوان ضریب انتشار (با واحد $$\text{m}^ {-1}$$) شناخته می‌شود.

با قرار دادن جواب در معادله (۱)، می‌توان $$\boldsymbol{I}(x)$$ را به دست آورد:

$$\large \frac { d } { d x } \left[ A _ { 1 } e ^ { \boldsymbol { \gamma } x } + A _ { 2 } e ^ { - \boldsymbol { \gamma } x } \right] = \boldsymbol { z } \boldsymbol { I } ( x ) \,$$

$$\large \Rightarrow \boldsymbol { I } ( x ) = \frac { A _ { 1 } e ^ { \gamma x } - A _ { 2 } e ^ { - \gamma x } }{ \boldsymbol { Z } _ { c } } \,$$

که در آن، $$\boldsymbol{Z}_{c} = \sqrt{\boldsymbol{\frac{z}{y}}}$$ امپدانس مشخصه یا امپدانس موج (برحسب $$\Omega$$) است.

می‌توانیم معادله بالا را برای ثوابت $$A_1$$ و $$A _ 2$$ با استفاده از شرایط مرزی در انتهای خط، یعنی $$x = 0 \,$$ و $$\boldsymbol{V}(0) = \boldsymbol{V_{r}} \,$$ و $$\boldsymbol{I}(0) = \boldsymbol{I_{r}} \,$$ محاسبه کنیم. جواب به صورت زیر خواهد بود:

$$\large A _ { 1 } = \frac { \boldsymbol { V _ { r } } + \boldsymbol { I _ { r } } \boldsymbol { Z } _ { c } } { 2 } \,$$

$$\large A _ { 2 } = \frac { \boldsymbol { V _ { r } } - \boldsymbol { I _ { r } } \boldsymbol { Z } _ { c } } { 2 } \,$$

با جایگذاری این ثوابت معادلات پارامترهای توزیع شده خط را به دست می‌آوریم:

$$\large \boldsymbol { V } ( x ) = \left ( \frac { \boldsymbol { V _ { r } } + \boldsymbol { I _ { r } } \boldsymbol { Z } _ { c } } { 2 } \right) e ^ { \boldsymbol { \gamma } x } + \left ( \frac { \boldsymbol { V _ { r } } - \boldsymbol { I _ { r } } \boldsymbol { Z } _ { c } } { 2 } \right ) e ^ { - \boldsymbol { \gamma } x } \, \; \; \; \; \; (5)$$

$$\large \boldsymbol { I } ( x ) = \left ( \frac { \boldsymbol { V _ { r } } + \boldsymbol { I _ { r } } \boldsymbol { Z } _ { c } } { 2 \boldsymbol { Z } _ { c } } \right ) e ^ { \gamma x } - \left ( \frac { \boldsymbol { V _ { r } } - \boldsymbol { I _ { r} } \boldsymbol { Z } _ { c } } { 2 \boldsymbol { Z } _ { c } } \right ) e ^ { - \gamma x } \, \; \; \; \; \; (6)$$

فرم هیپربولیک معادلات خط انتقال

معادلات (۵) و (۶) را می‌توان به صورت زیر بازنویسی کرد:

$$\large \boldsymbol { V } ( x ) = \left ( \frac { e ^ { \boldsymbol { \gamma } x } + e ^ { - \boldsymbol { \gamma } x } } { 2 } \right ) \boldsymbol { V _ { r} } + \boldsymbol { Z } _ { c } \left ( \frac { e ^ { \boldsymbol { \gamma } x } - e ^ { - \boldsymbol { \gamma } x } } { 2 } \right ) \boldsymbol { I _ { r } }$$

$$\large \boldsymbol { I } ( x ) = \frac { 1 } { \boldsymbol { Z } _ { c} } \left ( \frac { e ^ { \boldsymbol { \gamma } x } - e ^ { -\boldsymbol { \gamma} x } } { 2 } \right ) \boldsymbol { V _ { r } } + \left ( \frac { e ^ { \boldsymbol { \gamma } x } + e ^ { -\boldsymbol { \gamma } x } } { 2 } \right ) \boldsymbol { I _ { r } }$$

فرم نمایی توابع هیپربولیک $$\sinh x$$ و $$\cosh x$$ به صورت زیر است:

$$\large \sinh x = \frac { e ^ { x } - e ^ { - x } } { 2 }$$

$$\large \cosh x = \frac { e ^ { x } + e ^ { - x } } { 2 }$$

می‌توانیم از این روابط استفاده کنیم و معادلات خط انتقال را به فرم هیپربولیک بنویسیم:

$$\large \boldsymbol { V } ( x ) = \cosh ( \boldsymbol { \gamma } x ) \boldsymbol { V _ { r } } + \boldsymbol { Z } _ { c } \sinh ( \boldsymbol { \gamma } x ) \boldsymbol { I _ { r } }$$

$$\large \boldsymbol { I } ( x ) = \frac { 1 } { \boldsymbol { Z } _ { c } } \sinh ( \boldsymbol { \gamma } x ) \boldsymbol { V _ { r } } + \cosh ( \boldsymbol { \gamma } x ) \boldsymbol { I _ { r } }$$

برای خطی به طول $$l$$ متر، پارامترهای ABCD معادلات بالا را می‌توان به فرم ماتریسی زیر نوشت:

$$\large \left[ \begin {matrix} \boldsymbol { V _ { s } } \\ \\ \boldsymbol { I _ { s } } \end {matrix} \right ] = \left [ \begin {matrix} \cosh ( \boldsymbol { \gamma } l ) & \boldsymbol { Z } _ { c } \sinh ( \boldsymbol { \gamma } l ) \\ \\ \frac { 1 } { \boldsymbol { Z } _ { c } } \sinh ( \boldsymbol { \gamma } l ) & \cosh ( \boldsymbol { \gamma } l ) \end {matrix} \right] \left[ \begin {matrix} \boldsymbol { V _ { r } } \\ \\ \boldsymbol { I _ { r } } \end {matrix} \right] \,$$

که در آن، در ابتدای خط شرایط $$\boldsymbol{V_{s}} = \boldsymbol{V}(l) \,$$ و $$\boldsymbol{I_{s}} = \boldsymbol{I}(l) \,$$ را داریم.

مدل پارامتر توزیع شده خط با چند هادی

مدل پارامتر توزیع شده را می‌توان به یک خط با $$n$$ هادی تعمیم داد. برای این کار باید فازورهای ولتاژ و جریان را با بردارهای $$n \times 1$$ جایگزین کرد؛ یعنی برای یک خط سه فاز با سه هادی، داریم:

$$\large \boldsymbol { V } = \left[ \begin {matrix} \boldsymbol { V _ { a } } ( x ) \\ \boldsymbol { V _ { b } } ( x ) \\ \boldsymbol { V _ { c } } ( x ) \end {matrix} \right] \, , \boldsymbol { I } = \left[ \begin {matrix} \boldsymbol { I _ { a } } ( x ) \\ \boldsymbol { I _ { b } } ( x ) \\ \boldsymbol { I _ { c } } ( x ) \end {matrix} \right] \,$$

و امپدانس و ادمیتانس با ماتریس‌های مختلط $$n \times n$$ بیان می‌شوند. برای مثال، در یک خط سه فاز با سه هادی می‌توان نوشت:

$$\large [ Z ] = \left[ \begin {matrix} Z _ { a a } & Z _ { a b } & Z _ { a c } \\ Z _ { b a } & Z _ { b b } & Z _ { b c } \\ Z _ { c a } & Z _ { c b } & Z _ { c c } \end {matrix} \right] \,$$

$$\large [ Y ] = \left [ \begin {matrix} Y _ { a a } & Y _ { a b } & Y _ { a c } \\ Y _ { b a } & Y _ { b b } & Y _ { b c } \\ Y _ { c a } & Y _ { c b } & Y _ { c c } \end {matrix} \right] \,$$

معادلات (۱) و (۲) در مدل تکفاز را می‌توان برای چند هادی به صورت زیر بازنویسی کرد:

$$\large \frac { d \boldsymbol { V } } { d x} = [ Z ] \boldsymbol { I } \, \; \; \; \; \; ( 7 )$$

$$\large \frac { d \boldsymbol { I } } { d x } = [ Y ] \boldsymbol { V } \, \; \; \; \; \; ( 8 )$$

با مشتق‌گیری از این معادلات، داریم:

$$\large \frac { d ^ { 2 } \boldsymbol { V } } { d x ^ { 2 } } = [ Z ] \frac { d \boldsymbol { I } } { d x} \, \; \; \; \; \; (9)$$

$$\large \frac { d ^ { 2 } \boldsymbol { I } } { d x ^ { 2 } } = [ Y ] \frac { d \boldsymbol { V } } { d x} \, \; \; \; \; \; (10)$$

با جایگذاری معادله (۸) در معادله (۹) و معادله (۷) در معادله (۱۰)، مشابه معادلات (۳) و (۴)، برای چند هادی داریم:

$$\large \frac { d ^ { 2 } \boldsymbol { V } } { d x ^ { 2 } } = [ Z ] [ Y ] \boldsymbol { V } \, \; \; \; \; \; ( 1 1 )$$

$$\large \frac { d ^ { 2 } \boldsymbol { I } } { d x ^ { 2 } } = [ Y ] [ Z ] \boldsymbol { I } \, \; \; \; \; \; ( 1 2 )$$

این موضوع درباره خط‌هایی با چند هادی به این دلیل است که ماتریس‌های $$[Z]$$ و $$[ Y ]$$ کامل هستند و در نتیجه، ضرب $$[Z][Y]$$ با $$[Y][Z]$$ آن‌ها کامل خواهد بود. برای مثال، اگر معادله (۱۱) را بسط دهیم، داریم:

$$\large \left[ \begin {matrix} \frac { d ^ { 2 } \boldsymbol { V _ { a }} (x ) } {d x ^ { 2 }} \\ \\ \frac { d ^ { 2 } \boldsymbol { V _ { b } } (x ) }{ d x ^ {2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { V _ { c } } (x ) } {d x ^ { 2 } } \end {matrix} \right] = \left[ \begin {matrix} Z _ { a a } & Z _ { a b } & Z _ { a c } \\ Z _ { b a } & Z _ { b b } & Z _ { b c } \\ Z _ { c a } & Z _ { c b } & Z _ { c c } \end {matrix} \right] \left[ \begin{matrix} Y _ { a a } & Y _{ a b } & Y _ { a c } \\ Y _ { b a } & Y _ { b b } & Y _ { b c } \\ Y _ { c a } & Y _ { c b } & Y _ { c c } \end {matrix} \right] \left[ \begin {matrix} \boldsymbol { V _ { a } } ( x ) \\ \boldsymbol { V _ { b } } ( x ) \\ \boldsymbol { V _ { c } } ( x ) \end {matrix} \right] \,$$

خط اول دستگاه معادلات بالا را می‌توان به صورت زیر نوشت:

$$\large \begin {align*} \frac { d ^ { 2 } \boldsymbol { V _ { a } } ( x ) } { d x ^ { 2 } } & = \left ( Z _ { a a } Y _ { a a } + Z _ { a b } Y _ { b a } + Z _ { a c } Y _ { c a } \right ) \boldsymbol { V _ { a } } ( x ) \\ & \;\;\;\;\; + \left ( Z _ { a a } Y_ { a b } + Z _ { a b } Y _ { b b } + Z _ { a c } Y _ { c b } \right ) \boldsymbol { V _ { b } }( x ) \\ & \;\;\;\;\; + \left ( Z _ { a a } Y _ { a c } + Z _ { a b } Y _ { b c } + Z _ { a c } Y _ { c c } \right ) \boldsymbol { V _ { c } } ( x ) \, \end {align*}$$

برخلاف حالت تکفاز بالا، جواب عمومی به فرم بسته برای این معادله دیفرانسیل مرتبه دوم وجود ندارد (به دلیل تقاطع تزویج بین فازها). در نتیجه، به روشی موسوم به تبدیل مُدال (Modal Transformation) برای دکوپله کردن فازها از معادلات (۱۱) و (۱۲) نیاز خواهد بود.

تبدیل مدال

تبدیل مدال روشی برای دکوپله یا جدا کردن فازها از معادلات (۱۱) و (۱۲) بر اساس تجزیه مقادیر ویژه است. در این بخش، تبدیل مدال را از قواعد و اصول اولیه به دست خواهیم آورد.

تبدیلات خطی بردارهای ولتاژ و جریان را به صورت $$\boldsymbol{V'}$$ و $$\boldsymbol{I'}$$ در نظر بگیرید که برای سادگی فازهای ($$abc$$) به صورت مدهای ($$012$$) نوشته شده‌اند؛ یعنی برای یک خط سه فاز با سه هادی داریم:

$$\large \boldsymbol { V' } = \left [ \begin {matrix} \boldsymbol { V _ { 0 } } ( x ) \\ \boldsymbol { V _ { 1 } } ( x ) \\ \boldsymbol { V _ { 2 } } ( x ) \end {matrix} \right ] \, , \boldsymbol { I' } = \left [ \begin {matrix} \boldsymbol { I _ { 0 } } ( x ) \\ \boldsymbol { I _ { 1 } } ( x ) \\ \boldsymbol { I _ { 2 } } ( x ) \end {matrix} \right] \,$$

فرض کنید مقادیر اصلی به صورت زیر با مقادیر تبدیل شده مربوط می‌شوند:

$$\large \boldsymbol { V } = [ T _ { v } ] \boldsymbol { V' } \; \; \; \; \; (13)$$

$$\large \boldsymbol { I } = [ T _ { i } ] \boldsymbol { I' } \; \; \; \; \; ( 1 4 )$$

که در آن‌ها، $$[T_{v}] \,$$ و $$[T_{i}] \,$$ ماتریس‌های تبدیل $$n \times n$$ هستند. هنوز ماتریس‌های تبدیل را معرفی نکرده‌ایم، اما در ادامه خواهیم دید که این تبدیل‌ها در حقیقت، به ترتیب، بردار ویژه‌های $$[Z][Y] \,$$ و $$[Y][Z] \,$$ هستند.

با جایگذاری این مقادیر تبدیل شده در معادلات (۷) و (۸) داریم:

$$\large \frac { d [ T _ { v } ] \boldsymbol { V' } } { d x } = [ Z ] [ T _ { i } ] \boldsymbol { I ' } \,$$

$$\large \frac { d [ T _ { i } ] \boldsymbol { I' } } { d x } = [ Y ] [ T _ { v } ] \boldsymbol { V ' } \,$$

با فرض اینکه ماتریس‌های تبدیل $$[T_{v}] \,$$ و $$[T_{i}] \,$$ مستقل از $$x$$ هستند، می‌توانیم معادلات بالا را به فرم زیر بازنویسی کنیم:

$$\large \frac { d \boldsymbol { V' } } { d x } = [ T _ { v } ] ^ { - 1 } [ Z ] [ T _ { i } ] \boldsymbol { I' } \,$$

$$\large \frac { d \boldsymbol { I' } } { d x } = [ T _ { i } ] ^ { - 1 } [ Y ] [ T _ { v } ] \boldsymbol { V' } \,$$

با انجام فرایندی مشابه آنچه در بالا انجام دادیم، یعنی مشتق‌گیری از معادلات نسبت به $$x$$ و جایگذاری آن‌ها، خواهیم داشت:

$$\large \frac { d ^ { 2 } \boldsymbol { V' } } { d x ^ { 2 } } = [ T _ { v } ] ^ { - 1 } [ Z ] [ Y ] [ T _ { v } ] \boldsymbol { V' } \, \; \; \; \; \; (15)$$

$$\large \frac { d ^ { 2 } \boldsymbol { I' } } { d x ^ { 2 } } = [ T _ { i } ] ^ { - 1 } [ Y ] [ Z ] [ T _ { i } ] \boldsymbol { I' } \, \; \; \; \; \; ( 1 6 )$$

برای دکوپله‌سازی فازها در معادلات (۱۵) و (۱۶)، باید $$[T_{v}]^{-1} [Z] [Y] [T_{v}] \,$$ و $$[T_{i}]^{-1} [Y] [Z] [T_{i}] \,$$ ماتریس‌هایی قطری باشند؛ یعنی:

$$\large \text {diag} ( \boldsymbol { \lambda _ { v } }) = [ T _ { v } ] ^ { - 1 } [ Z ] [ Y ] [ T _ { v } ] \,$$

$$\large \text {diag} ( \boldsymbol { \lambda _ { i } } ) = [ T _ { i } ] ^ { - 1 } [ Y ] [ Z ] [ T _ { i } ] \,$$

واضح است که ماتریس تبدیل $$[T_{v}] \,$$ و ماتریس قطری $$\text{diag}(\boldsymbol{\lambda_{v}})$$، به ترتیب، بردارهای ویژه و مقادیر ویژه $$[Z][Y] \,$$ هستند.

علاوه بر این، از آنجایی که ماتریس‌های $$[Z] \,$$ و $$[Y] \,$$ هر دو متقارن هستند، داریم: $$[Z][Y] = \left( [Y][Z] \right)^{T} \,$$. می‌دانیم که مقادیر ویژه یک ماتریس و ترانهاده آن مشابه هستند، بنابراین، $$[Z][Y] \,$$ و $$[Y][Z] \,$$ نیز مقادیر ویژه مشترکی دارند؛ یعنی:

$$\large \text {diag} ( \boldsymbol { \lambda _ { v } } ) = \text{diag} ( \boldsymbol { \lambda _ { i } } ) = \text{diag} ( \boldsymbol { \lambda } ) \,$$

اکنون می‌توانیم معادلات (۱۵) و (۱۶) را به صورت زیر بازنویسی کنیم:

$$\large \left[ \begin {matrix} \frac { d ^ { 2 } \boldsymbol { V _ { 0 } } ( x ) } { d x ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { V _ { 1 } } ( x ) } { d x ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { V _ { 2 } } ( x ) } { d x ^ { 2 } } \end {matrix} \right] = \left[ \begin {matrix} \lambda _ { 0 } & & \\ & \lambda _ { 1 } & \\ & & \lambda _ { 2 } \end {matrix} \right ] \left [ \begin {matrix} \boldsymbol { V _ { 0 } } ( x ) \\ \boldsymbol { V _ { 1 } } ( x ) \\ \boldsymbol { V _ { 2 } } ( x ) \end {matrix} \right] \, \; \; \; \; \; ( 1 7 )$$

$$\large \left[ \begin {matrix} \frac { d ^ { 2 } \boldsymbol { I _ { 0 } } ( x ) } { d x ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { I _ { 1 } } ( x ) } { d x ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { I _ { 2 } } ( x ) } { d x ^ { 2 } } \end {matrix} \right ] = \left [ \begin {matrix} \lambda _ { 0 } & & \\ & \lambda _ { 1 } & \\ & & \lambda _ { 2 } \end {matrix} \right] \left[ \begin {matrix} \boldsymbol { I _ { 0 } } ( x ) \\ \boldsymbol { I _ { 1 } } ( x ) \\ \boldsymbol { I _ { 2 } } ( x ) \end {matrix} \right ] \, \; \; \; \; \; ( 1 8 )$$

با یادآوری حالت تکفاز که ثابت انتشار آن به صورت $$\boldsymbol{\gamma} = \sqrt{\boldsymbol{zy}}$$ تعریف می‌شود، در فرم ماتریسی با چند هادی، می‌توانیم یک ماتریس انتشار $$[\Gamma] \,$$ به صورت زیر تعریف کنیم:

$$\large [ \Gamma ] = ( [ Z ] [ Y ] ) ^ { \frac { 1 } { 2 } } \,$$

فرض می‌کنیم $$\gamma_0$$، $$\gamma_1$$ و $$\gamma_2$$ مقادیر ویژه ماتریس انتشار  $$[\Gamma] \,$$ باشند.

یکی از ویژگی‌های مقدار ویژه این است که اگر ماتریس $$A$$ دارای مقادیر ویژه $$\lambda _ 1$$، $$\lambda _ 2$$، $$\cdots$$ و $$\lambda _ n$$ باشد، آن‌گاه $$A^{k} \,$$ دارای مقادیر ویژه $$\lambda_1^{k}$$، $$\lambda_2^{k}$$، $$\cdots$$ و $$\lambda_n^{k}$$ است.

بنابراین، از آنجایی که $$\lambda _ 0$$، $$\lambda _ 1$$ و $$\lambda _ 2$$ مقادیر ویژه $$[Z][Y] \,$$ و $$\gamma_0$$، $$\gamma_1$$ و $$\gamma_2$$ بردار ویژه‌های $$([Z][Y])^{\frac{1}{2}} \,$$ هستند، داریم:

$$\large \left[ \begin {matrix} \lambda _ { 0 } & & \\ & \lambda _ { 1 } & \\ & & \lambda _ { 2 } \end {matrix} \right] = \left[ \begin {matrix} \gamma _ { 0 } ^ { 2 } & & \\ & \gamma _ { 1 } ^ { 2 } & \\ & & \gamma _ { 2 } ^ { 2 } \end {matrix} \right] \,$$

می‌توانیم معادلات (۱۷) و (۱۸) را به صورت زیر بنویسیم:‌

$$\large \left[ \begin {matrix} \frac { d ^ { 2 } \boldsymbol { V _ { 0 } } ( x ) } { d x ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { V _ { 1 } } ( x ) } { dx ^ { 2} } \\ \\ \frac { d ^ { 2 } \boldsymbol { V _ { 2 } } ( x ) } { d x ^ { 2} } \end {matrix} \right ] = \left [ \begin {matrix} \gamma _ { 0 } ^ { 2 } & & \\ & \gamma _ { 1 } ^ { 2 } & \\ & & \gamma _ { 2 } ^ { 2 } \end {matrix} \right] \left[ \begin {matrix} \boldsymbol { V _ { 0 } } ( x ) \\ \boldsymbol { V _ { 1 } } ( x ) \\ \boldsymbol { V _ { 2 } } ( x ) \end {matrix} \right] \, \; \; \; \; \; ( 1 9 )$$

$$\large \left [ \begin {matrix} \frac { d ^ { 2 } \boldsymbol { I _ { 0 } } ( x ) } { d x ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { I _ { 1 } } ( x ) } { d x ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { I _ { 2 } } ( x ) } { d x ^ { 2 } } \end {matrix} \right ] = \left [ \begin {matrix} \gamma _ { 0 } ^ { 2 } & & \\ & \gamma _ { 1 } ^ { 2 } & \\ & & \gamma _ { 2 } ^ { 2 } \end {matrix} \right] \left [ \begin {matrix} \boldsymbol { I _ { 0 } } ( x ) \\ \boldsymbol { I _ { 1 } } ( x ) \\ \boldsymbol { I _ { 2 } } ( x ) \end {matrix} \right ] \, \; \; \; \; \; ( 2 0 )$$

اکنون هر کدام از این معادلات دیفرانسیل دکوپله مدال بالا را می‌توان با استفاده از جواب عمومی زیر حل کرد:‌

$$\large \begin {align*} \boldsymbol { V _ { 0 } } ( x ) & = A _ { 0 } e ^ { \gamma _ 0 x } + B _ { 0 } e ^ { - \gamma _ 0 x } \, \\ \boldsymbol { V _ { 1 } } ( x ) & = A _ { 1 } e ^ { \gamma _ 1 x } + B _ { 1 } e ^ { - \gamma _ 1 x } \, \\ \boldsymbol { V _ { 2 } } ( x ) & = A _ { 2 } e ^ { \gamma _ 2 x } + B _ { 2 } e ^ { - \gamma _ 2 x } \, \end {align*}$$

با مشتق‌گیری از معادلات بالا نسبت به $$x$$ داریم:

$$\large \left[ \begin {matrix} \frac { d \boldsymbol { V _ { 0 } } ( x ) } { d x } \\ \\ \frac { d \boldsymbol { V _ { 1 } } ( x ) }{ d x } \\ \\ \frac { d \boldsymbol { V _ { 2 } } ( x ) } { d x } \end {matrix} \right] = \left[ \begin {matrix} \gamma _ { 0 } & & \\ & \gamma _ { 1 } & \\ & & \gamma _ { 2 } \end {matrix} \right ] \left[ \begin {matrix} A _ { 0 } e ^ { \gamma _ 0 x } - B _ { 0 } e ^ { - \gamma _ 0 x } \\ A _ { 1 } e ^ { \gamma _ 1 x } - B _ { 1 } e ^ { - \gamma _ 1 x } \\ A _ { 2 } e ^ { \gamma _ 2 x } - B _ { 2 } e ^ { - \gamma _ 2 x } \end {matrix} \right] \, \; \; \; \; \; ( 2 1 )$$

معادله (۲۱) بالا را به فرم استاندارد زیر می‌نویسیم:

$$\large \frac { d \boldsymbol { V' } } { d x } = [\gamma] \boldsymbol { V _ x } \, \; \; \; \; \; ( 2 2 )$$

بنابراین، می‌توان نوشت:

$$\large \frac { d \boldsymbol { V' } } { d x } = [ T _ { v } ] ^ { - 1 } [ Z ] [ T _ { i } ] \boldsymbol { I' } \,$$

با برابر قرار دادن معادله اخیر و معادله (۲۲) و حل آن برای $$\boldsymbol{V_x}$$ داریم:

$$\large \boldsymbol { V _ x } = [\gamma] ^ { - 1 } [ T _ { v } ] ^ { - 1 } [ Z ] [ T _ { i } ] \boldsymbol { I' } \,$$

ماتریس امپدانس مشخصه مدال (یا ماتریس امپدانس موج مدال) را به صورت زیر تعریف می‌کنیم:

$$\large [ Z _ c ] = [ \gamma ] ^ { - 1 } [ T _ { v } ] ^ { - 1 } [ Z ] [ T _ { i } ] \, \; \; \; \; \; ( 2 3 )$$

با استفاده از این تعریف، بردار جریان مدال را می‌توانیم به صورت زیر بنویسیم:

$$\large \boldsymbol { I' } = [ Z _ c ] ^ { - 1 } \boldsymbol { V _ x } \, \; \; \; \; \; (24)$$

می‌توان نشان داد که اگر $$[\gamma]$$ قطری باشد، آنگاه $$[Z_c]$$ نیز قطری خواهد بود. بنابراین، معادله (۲۴) به صورت زیر در خواهد آمد:

$$\large \left[ \begin {matrix} \boldsymbol { I _ { 0 } } ( x ) \\ \boldsymbol { I _ { 1 } } ( x ) \\ \boldsymbol { I _ { 2} } (x ) \end {matrix} \right] = \left[ \begin {matrix} \frac { 1 } { \boldsymbol { Z _ 0 } } & & \\ & \frac { 1 } { \boldsymbol { Z _ 1 } } & \\ & & \frac { 1 } { \boldsymbol { Z _ 2 } } \end{matrix} \right] \left[ \begin{matrix} A_{0} e^{\gamma_0 x} - B_{0} e^{-\gamma _ 0 x } \\ A _ { 1 } e ^ { \gamma _ 1 x } - B _ { 1 } e ^ { - \gamma _ 1 x } \\ A _ { 2 } e ^ { \gamma _ 2 x } - B _ { 2 } e ^ { - \gamma _ 2 x } \end {matrix} \right] \, \; \; \; \; \; ( 2 5 )$$

شرایط مرزی

اکنون شش معادله مدال داریم که می‌توانیم آن‌ها را با استفاده از شرایط اولیه زیر حل کنیم:

$$\large \left[ \begin {matrix} \boldsymbol { V _ { 0 } } ( x ) \\ \boldsymbol { V _ { 1 } } ( x ) \\ \boldsymbol { V _ { 2 } } ( x ) \end{matrix} \right] = \left[ \begin {matrix} A _ { 0 } e ^ { \gamma _ 0 x } + B _ { 0 } e ^ { - \gamma _ 0 x } \\ A _ { 1 } e ^ { \gamma _ 1 x } + B _ { 1 } e ^ { - \gamma _ 1 x } \\ A _ { 2 } e ^ { \gamma _ 2 x } + B _ { 2 } e ^ { - \gamma _ 2 x } \end {matrix} \right] \,$$

$$\large \left[ \begin {matrix} \boldsymbol { I _ { 0 }} ( x ) \\ \boldsymbol { I _ { 1 } } ( x ) \\ \boldsymbol { I _ { 2 } } ( x ) \end {matrix} \right] = \left[ \begin {matrix} \frac { 1 } { \boldsymbol { Z _ 0 } } & & \\ & \frac { 1 } { \boldsymbol { Z _ 1 } } & \\ & & \frac { 1 } { \boldsymbol { Z _ 2 } } \end {matrix} \right] \left[ \begin {matrix} A _ { 0 } e ^ { \gamma _ 0 x } - B _ { 0 } e ^ { - \gamma _ 0 x } \\ A _ { 1 } e ^ { \gamma _ 1 x } - B _ { 1 } e ^ { - \gamma _ 1 x } \\ A _ { 2 } e ^ { \gamma _ 2 x } - B _ { 2 } e ^ { - \gamma _ 2 x } \end {matrix} \right] \,$$

شرایط مرزی $$\boldsymbol{V_r}$$ و $$\boldsymbol{I_r}$$ را باید به صورت زیر به مقادیر مدال تبدیل کنیم:

$$\large \boldsymbol { V _ r }' = [ T _ v ] ^ { - 1 } \boldsymbol { V _ r }$$

$$\large \boldsymbol { I _ r }' = [ T _ i ] ^ { - 1 } \boldsymbol { I _ r }$$

در نقطه دریافت (یعنی $$x = 0$$)، معادلات مدال مطابق زیر کاهش می‌یابند:

$$\large \left[ \begin {matrix} \boldsymbol { V _ { 0 r } } \\ \boldsymbol { V _ { 1 r } } \\ \boldsymbol { V _ { 2 r } } \end {matrix} \right] = \left[ \begin {matrix} A _ { 0 } + B _ { 0 } \\ A _ { 1 } + B _ { 1 } \\ A _ { 2 } + B _ { 2 } \end {matrix} \right] \,$$

$$\large \left[ \begin {matrix} \boldsymbol { Z _ 0 } \boldsymbol { I _ { 0 r } } \\ \boldsymbol { Z _ 1 } \boldsymbol { I _ { 1 r } } \\ \boldsymbol { Z _ 2 } \boldsymbol { I _ { 2 r } } \end {matrix} \right] = \left[ \begin {matrix} A _ { 0 } - B _ { 0 } \\ A _ { 1 } - B _ { 1 } \\ A _ { 2 } - B _ { 2 } \end {matrix} \right] \,$$

جواب ثابت‌های $$[A]$$ و $$[B]$$ به صورت زیر است:‌

$$\large \left[ \begin {matrix} A _ { 0 } \\ A _ { 1 } \\ A _ { 2 } \end {matrix} \right] = \frac { 1 } { 2 } \left[ \begin {matrix} \boldsymbol { V _ { 0 r } } - \boldsymbol { Z _ 0 } \boldsymbol { I _ { 0 r } } \\ \boldsymbol { V _ { 1 r } } - \boldsymbol { Z _ 1 } \boldsymbol { I _ { 1 r } } \\ \boldsymbol { V _ { 2 r } } - \boldsymbol { Z _ 2 } \boldsymbol { I _ { 2 r } } \end {matrix} \right] \, \; \; \; \; \; ( 2 6 )$$

$$\large \left[ \begin {matrix} B _ { 0 } \\ B _ { 1 } \\ B _ { 2 } \end {matrix} \right] = \frac { 1 } { 2 } \left[ \begin {matrix} \boldsymbol { V _ { 0 r } } + \boldsymbol { Z _ 0 } \boldsymbol { I _ { 0 r } } \\ \boldsymbol { V _ { 1 r } } + \boldsymbol { Z _ 1 } \boldsymbol { I _ { 1 r } } \\ \boldsymbol { V _ { 2 r } } + \boldsymbol { Z _ 2 } \boldsymbol { I _ { 2 r } } \end {matrix} \right] \, \;\;\; \; \; ( 2 7 )$$

این ثابت‌ها را می‌توان در معادلات ولتاژ و جریان مدال قرار داد و عبارات نهایی را محاسبه کرد:

$$\large \left[ \begin {matrix} \boldsymbol { V _ { 0 } } ( x ) \\ \boldsymbol { V _ { 1 } } ( x ) \\ \boldsymbol { V _ { 2 } } ( x ) \end{matrix} \right] = \frac { 1 } { 2 } \left[ \begin {matrix} ( \boldsymbol { V _ { 0 r } } - \boldsymbol { Z _ 0 } \boldsymbol { I _ { 0 r } } ) e ^ { \gamma _ 0 x } + ( \boldsymbol { V _ { 0 r } } + \boldsymbol { Z _ 0 } \boldsymbol { I _ { 0 r } } ) e ^ { -\gamma _ 0 x } \\ ( \boldsymbol { V _ { 1 r } } - \boldsymbol { Z _ 1 } \boldsymbol { I _ { 1 r } } ) e ^ { \gamma _ 1 x } + ( \boldsymbol { V _ { 1 r } } + \boldsymbol { Z _ 1 } \boldsymbol { I _ { 1 r } } ) e ^ { - \gamma _ 1 x } \\ ( \boldsymbol { V _ { 2 r } } - \boldsymbol { Z _ 2 } \boldsymbol { I _ { 2 r } } ) e ^ { \gamma _ 2 x } + ( \boldsymbol { V _ { 2 r } } + \boldsymbol { Z _ 2 } \boldsymbol { I _ { 2 r } } ) e ^ { - \gamma _ 2 x } \end {matrix} \right] \, \; \; \; \; \; ( 2 8 )$$

$$\large \left[ \begin {matrix} \boldsymbol { I _ { 0 } } ( x ) \\ \boldsymbol { I _ { 1 } } ( x ) \\ \boldsymbol { I _ { 2 } } ( x ) \end {matrix} \right] = \left[ \begin {matrix} \frac { 1 } { 2 \boldsymbol { Z _ 0 } } & & \\ & \frac { 1 } { 2 \boldsymbol { Z _ 1 } } & \\ & & \frac { 1 } { 2 \boldsymbol { Z _ 2 } } \end {matrix} \right] \left[ \begin {matrix} ( \boldsymbol { V _ { 0 r } } - \boldsymbol { Z _ 0 } \boldsymbol { I _ { 0 r } } ) e ^ { \gamma _ 0 x } - ( \boldsymbol { V _ { 0 r } } + \boldsymbol { Z _ 0 } \boldsymbol { I _ { 0 r } } ) e ^ { - \gamma _ 0 x } \\ ( \boldsymbol { V _ { 1 r } } - \boldsymbol { Z _ 1 } \boldsymbol { I _ { 1 r } } ) e ^ { \gamma _ 1 x } - ( \boldsymbol { V _ { 1 r } } + \boldsymbol { Z _ 1 } \boldsymbol { I _ { 1 r} } ) e ^ { - \gamma _ 1 x } \\ ( \boldsymbol { V _ { 2 r } } - \boldsymbol { Z _ 2 } \boldsymbol { I _ { 2 r } } ) e ^ { \gamma _ 2 x } - ( \boldsymbol { V _ { 2 r } } + \boldsymbol { Z _ 2 } \boldsymbol { I _ { 2 r } } ) e ^ { - \gamma _ 2 x } \end {matrix} \right] \, \; \; \; \; \; ( 2 9 )$$

فرم هیپربولیک معادلات خط با چند هادی

مشابه مدل با پارامتر توزیع شده تکفاز، ولتاژها و جریان‌ها نهایی نشان داده شده در معادلات (۲۸) و (۲۹) را می‌توان به فرم هیپربولیک تبدیل کرد:

$$\large \begin {align*} \left[ \begin {matrix} \boldsymbol { V _ { 0 } } ( x ) \\ \boldsymbol { V _ { 1 } } ( x ) \\ \boldsymbol { V _ { 2 } } ( x ) \end {matrix} \right] & = \left[ \begin {matrix} \cosh { ( \gamma _ 0 x ) } & & \\ & \cosh { ( \gamma _ 1 x ) } & \\ & & \cosh { ( \gamma _ 2 x ) } \end {matrix} \right] \left[ \begin {matrix} \boldsymbol { V _ { 0 r } } \\ \boldsymbol { V _ { 1 r } } \\ \boldsymbol { V _ { 2 r } } \end {matrix} \right] \\ & \;\;\; \;+ \left[ \begin {matrix} \boldsymbol { Z _ 0 } \sinh { ( \gamma _ 0 x ) } & & \\ & \boldsymbol { Z _ 1 } \sinh { ( \gamma _ 1 x ) } & \\ & & \boldsymbol { Z _ 2 } \sinh { ( \gamma _ 2 x ) } \end {matrix} \right] \left[ \begin {matrix} \boldsymbol { I _ { 0 r } } \\ \boldsymbol { I _ { 1 r } } \\ \boldsymbol { I _ { 2 r } } \end {matrix} \right] \, \; \; \; \; \; ( 3 0 ) \end {align*}$$

$$\large \begin {align*} \left[ \begin {matrix} \boldsymbol { I _ { 0 } } ( x ) \\ \boldsymbol { I _ { 1 } } ( x ) \\ \boldsymbol { I _ { 2} } ( x ) \end {matrix} \right] & = \left[ \begin {matrix} \frac { 1 } { \boldsymbol { Z _ 0 } } \sinh { ( \gamma _ 0 x ) } & & \\ & \frac { 1 } { \boldsymbol { Z _ 1 } } \sinh { ( \gamma _ 1 x ) } & \\ & & \frac { 1 } { \boldsymbol {Z _ 2 } } \sinh { ( \gamma _ 2 x ) } \end {matrix} \right] \left[ \begin{matrix} \boldsymbol { V _ { 0 r } } \\ \boldsymbol { V _ { 1 r } } \\ \boldsymbol { V _ { 2 r } } \end {matrix} \right] \\ & \;\;\;\;+ \left[ \begin {matrix} \cosh { ( \gamma _ 0 x ) } & & \\ & \cosh { ( \gamma _ 1 x ) } & \\ & & \cosh { ( \gamma _ 2 x ) } \end {matrix} \right] \left[ \begin {matrix} \boldsymbol { I _ { 0 r } } \\ \boldsymbol { I _ { 1 r } } \\ \boldsymbol { I _ { 2 r } } \end {matrix} \right] \, \; \; \; \; \; ( 3 1 ) \end {align*}$$

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• سیستم پریونیت (Per-Unit) — از صفر تا صد
• پخش بار در سیستم قدرت — مفاهیم و معادلات
• مدار سه فاز — از صفر تا صد

^^