مدار موازی چیست؟ — به زبان ساده با شکل و مثال
در این مطلب مدار موازی را بررسی میکنیم و تغییرات ولتاژ و جریان را در این مدار مورد تجزیه و تحلیل قرار میدهیم. همچنین در مورد مقاومت، خازن و سلف یا القاگر که در یک مدار به صورت موازی متصل شده باشند نیز صحبت خواهیم کرد.
مدار موازی
در این نوشتار در ابتدا سه اصل مهمی که در مورد مدارهای موازی برقرار است را بیان خواهیم کرد. بر این اساس در یک مدار موازی همواره بین ولتاژ، جریان و مقاومت روابط زیر برقرار است:
- ولتاژ: در یک مدار موازی همواره ولتاژ دو سر اجزایی که به صورت موازی به یکدیگر متصل شدهاند با هم برابر است.
- جریان: در یک مدار موازی جریان کل مدار برابر با مجموع جریان اجزایی از مدار است که به صورت موازی متصل شدهاند.
- مقاومت: در یک مدار موازی که اجزای آن به صورت موازی متصل شدهاند، مقدار مقاومت معادل از هر یک از مقاومتهای منفرد کوچکتر است.
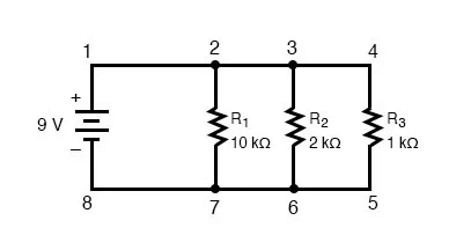
در ادامه چند نمونه از مدارهای موازی را بررسی میکنیم و تغییرات پارامترهای مختلف این مدارها را جستجو میکنیم. همان طور که میدانید اجزای یک مدار را میتوان به صورت متوالی یا سری، موازی یا ترکیبی از این دو به یکدیگر متصل کرد. برای مطالعه در مورد مدارهای متوالی یا سری مطلب مدار متوالی چیست؟ را مطالعه کنید. برای بحث در مورد مدارهای موازی با یک مدار موازی متشکل از سه مقاومت الکتریکی و یک باتری شروع میکنیم.
ولتاژ در مدارهای موازی
اولین اصل مدارهای موازی این است که ولتاژ دو سر اجزایی از مدار که موازی با یکدیگر قرار گرفتهاند با یکدیگر برابر است. این ویژگی به این دلیل است که تنها دو نقطه مشترک الکتریکی در اجزای یک مدار الکتریکی موازی وجود دارد که مقدار آنها باید در هر زمانی یکسان باشد.
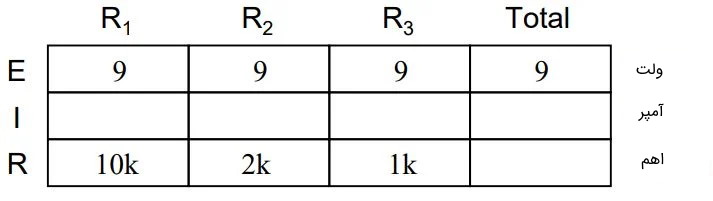
بدین ترتیب در مدار داده شده در تصویر (۱)، ولتاژ دو سر مقاومت $$R_1$$ برابر با ولتاژ دو سر مقاومت $$R_2$$ است، که این ولتاژ نیز برابر با ولتاژ دو سر مقاومت $$R_3$$ اندازهگیری میشود. از این موضوع میتوان نتیجه گرفت که ولتاژ دو سر هر یک از مقاومتهای موازی برابر با ولتاژ دو سر باتری و ۹ ولت است. این موضوع در جدول زیر به خوبی نشان داده شده است:
کاربرد قانون اهم در یک مدار موازی ساده
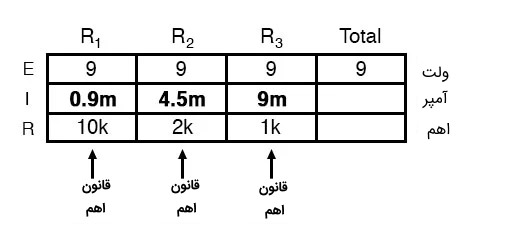
مانند مدار متوالی قانون اهم برای مدار موازی نیز برقرار است و با دانستن مقدار ولتاژ، جریان و مقاومت در یک مدار میتوان از قانون اهم استفاده کرد. مشخص است که در مدار مورد بحث در تصویر (۱) و با استفاده از جدول بالا به راحتی میتوان قانون اهم را برای هر یک از مقاومتها به کار برد و داریم:
$$\large \begin{array}{l}
\mathrm{I}_{\mathrm{R} 1}=\frac{\mathrm{E}_{\mathrm{R} 1}}{\mathrm{R}_{1}} \quad \mathrm{I}_{\mathrm{R} 2}=\frac{\mathrm{E}_{\mathrm{R} 2}}{\mathrm{R}_{2}} \quad \mathrm{I}_{\mathrm{R} 3}=\frac{\mathrm{E}_{\mathrm{R3}}}{\mathrm{R}_{3}} \\
\mathrm{I}_{\mathrm{R} 1}=\frac{9 \mathrm{~V}}{10 \mathrm{k} \Omega}=0.9 \mathrm{~mA} \\
\mathrm{I}_{\mathrm{R} 2}=\frac{9 \mathrm{~V}}{2 \mathrm{k} \Omega}=4.5 \mathrm{~m} \mathrm{~A} \\
\mathrm{I}_{\mathrm{R} 3}=\frac{9 \mathrm{~V}}{1 \mathrm{k} \Omega}=9 \mathrm{~mA}
\end{array}$$
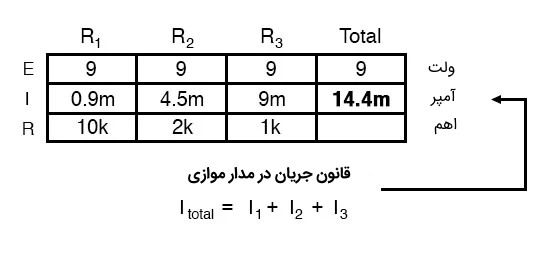
در این مرحله هنوز مقدار مقاومت یا جریان را برای ستون آخر نمیدانیم و نمیتوانیم از قانون اهم برای این ستون استفاده کنیم. اما اگر دقت کنیم میتوانیم مقدار جریان را برای ستون آخر به دست آوریم، با توجه به اصل دوم گفته شده در مورد مدارهای موازی که جریان کل برابر با مجموع جریان دو سر هر قسمت از مدار است، میتوانیم جریان کل را به دست آوریم.
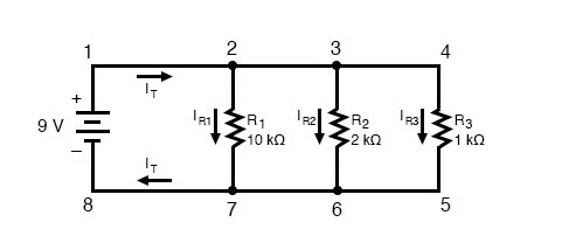
جریان خروجی از پایانه مثبت باتری در نقطه ۲ دو شاخه میشود و مقداری از جریان از مقاومت $$R_1$$ عبور میکند، این روند در نقطه ۳ نیز تکرار میشود و جریان مجدداً به دو شاخه تبدیل میشود و جریان باقیمانده از جریان کل از مقاومت $$R_3$$ عبور میکند. جریانهای عبوری از این مقاومتها مجدداً در نقاط تقاطع مدار بعد از عبور از مقاومتهای $$R_1$$، $$R_2$$ و $$R_3$$ به هم میپیوندند و در نقطه ۷ مدار، جریان خروجی از پایانه مثبت باتری به پایانه منفی باتری وارد میشود.
این همان اصل دوم مدارهای موازی است که جریان کل مدار برابر با مجموع جریانهای عبوری از هر یک از اجزای مدار موازی است. با استفاده از این اصل جدول مدار ارائه شده در تصویر (۱) به شکل زیر در میآید:
مقاومت کل در مدار موازی
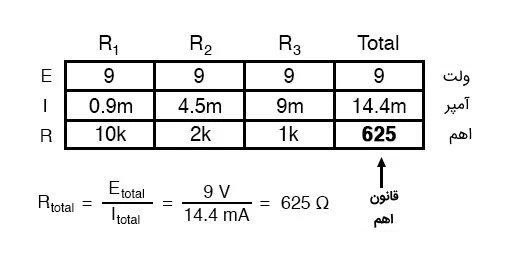
در نهایت با استفاده از قانون اهم میتوانیم مقاومت کل را در یک مدار موازی محاسبه کنیم و داریم:
محاسبه مقاومت معادل در یک مدار موازی
نکته بسیار مهم در محاسبه مقاومت کل مدار موازی این است که مقدار این مقاومت تنها ۶۲۵ اهم است که از هر یک از مقاومتهای داده شده در مدار کوچکتر است. این در حالی است که در مدار متوالی یا سری مقاومت کل از هر یک از مقاومتهای منفرد مدار بزرگتر بود و مجموع مقاومتهای مدار برابر با مقاومت معادل یا کل در مدار متوالی بود.
این ویژگی ما را به اصل سوم مدارهای موازی رهنمون میکند. در حقیقت باید گفت مقاومت معادل یا کل یک مدار موازی به بیان ریاضی به صورت زیر است:
$$\large \mathrm{R}_{\text {total }}=\frac{1}{\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}+\frac{1}{\mathrm{R}_{3}}}$$
مشخص است که رابطه بالا برای مداری با بیش از سه مقاومت که به صورت موازی به یکدیگر متصل باشند نیز برقرار است.
اتصال خازن در مدار موازی
تصویر (۳-الف) اتصال سه خازن به صورت موازی را نشان میدهد. در این اتصال محاسبه ظرفیت خازن معادل آسانتر از حالت متوالی یا سری است. برای محاسبه ظرفیت خازن معادل موازی یا $$C_p$$ باید توجه کرد که ولتاژ دو سر هر یک از ظرفیتها $$V$$ و برابر با ولتاژ دو سر باتری یا منبع است. بدین ترتیب میتوان گفت مجموع بار ذخیره شده در مدار موازی برابر با مجموع بارهای هر یک از خازنها و برابر با $$Q=Q_1+Q_2+Q_3$$ است.
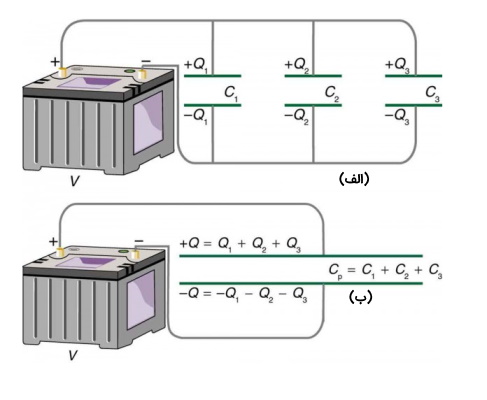
با استفاده از رابطه $$Q=CV$$ و این ویژگی که بار کل روی خازنها برابر با مجموع بارهای روی هر یک از خازنها است داریم:
$$\large \begin{cases}Q_1=C_1V\\ Q_2=C_2V\Rightarrow C_pV=C_1V+C_2V+C_3V\\ Q_3=C_3V\end{cases}$$
با حذف ولتاژ از طرفین رابطه بالا، رابطه زیر برای ظرفیت معادل خازن به دست میآید و داریم:
$$\large C_p=C_1+C_2+C_3+\dots$$
بدین ترتیب اگر ظرفیت سه خازن داده شده در تصویر (۳) به ترتیب برابر با ۱، ۵ و ۸ میکروفارادی باشد ظرفیت خازن معادل برابر با ۱۴ میکروفارادی است که تصویر این خازن معادل در تصویر (۳-ب) نمایش داده شده است.
اتصال القاگر یا سلف در مدار موازی
القاگرها را در اتصال موازی با یکدیگر میگوییم زمانی که هر ترمینال یک القاگر به ترمینال القاگر یا القاگرهای دیگری متصل باشد. در این حالت مانند خازنها اندوکتانس یا القای کل مدار کمتر از القای هر یک از القاگرها به تنهایی است.
وقتی القاگرها به صورت موازی به یکدیگر متصل میشوند، شارش جریان در هر یک از القاگرها دقیقاً برابر با جریان کل مدار نیست، اما مجموع جریان هر یک از القاگرها برابر با جریان کل است.
در حقیقت وقتی جریان ورودی به یک القاگر کمتر از جریان کل باشد بدین معنا است که میدان مغناطیسی در هر یک از القاگرها کمتر از میدانی است که توسط جریان کل در مدار ایجاد میشود.
این موضوع در مورد مقاومتهای موازی نیز بدین صورت است که جریان بیشتری از مقاومت کمتر عبور میکند زیرا که مقاومت کوچکتر کمترین مخالفت را در برابر شارش جریان نشان میدهد.
به همین ترتیب وقتی القاگرها به صورت موازی متصل هستند جریان چه در مدار در حال کاهش باشد چه در حال افزایش، مسیری با کمترین مخالفت را برای عبور انتخاب میکند. این در حالی است که هر یک از القاگرها نیز به طور جداگانه با تغییر جریان مخالفت میکنند.
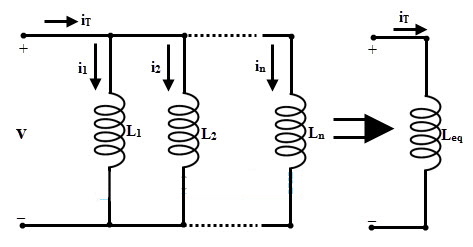
در اتصال موازی، ولتاژ در دو سر هر القاگر برابر است. با معرفی این ویژگی در مورد اتصال موازی القاگرها، در ادامه اتصال سه القاگر به صورت موازی در یک مدار را بررسی میکنیم. در این حالت هیچ جفت شدگی مغناطیسی بین القاگرها وجود ندارد.
در این اتصال که هیچ جفت شدگی مغناطیسی بین القاگرها وجود ندارد، القای کل برابر القای متقابل هر یک از القاگرها یا سلفها است. این ویژگی را میتوان به صورت زیر تحلیل کرد. همان طور که در مورد استفاده از قانون اهم در مدار موازی گفتیم، جریان کل در یک مدار موازی برابر با مجموع جریانهای هر یک از اجزای مدار است که به صورت موازی بسته شده است. بدین ترتیب داریم:
$$\large I_{\text {Total }}=I_{L 1}+I_{L 2}+I_{L 3} \ldots \ldots+I_{n}$$
همچنین در مورد ولتاژ دو سر هر یک از اجزای مدار موازی بیان کردیم که ولتاژ دو سر هر یک از اجزای مدار موازی با یکدیگر برابر هستند و داریم:
$$\large \mathrm{V}_{\text {Total }}=\mathrm{V}_{\mathrm{L1}}=\mathrm{V}_{\mathrm{L2}} =\mathrm{V}_{\mathrm{L3}} \ldots =\mathrm{V}_{\mathrm{n}}$$
افت ولتاژ در دو سر هر یک از القاگرها را میتوان با رابطه $$V=L\frac{di}{dt}$$ بیان کرد و در نتیجه برای افت ولتاژ کل داریم:
$$\large \begin{cases}V_T=L_T\frac{dI_{Total}}{dt}\\
\Rightarrow\frac{V_T}{L_T}=\frac{d}{dt}(I_{L1}+I_{L2}+I_{L3}+\dots+I_{Ln})\end{cases}$$
اگر به جای تغییرات جریان هر یک از القاگرها از رابطه $$\frac{V}{L}$$ استفاده کنیم، رابطه بالا به شکل زیر در میآید:
$$\large V_{T}=L_{T}\left(V / L_{1}+V / L_{2}+V / L_{3} \ldots\right)$$
با حذف ولتاژ از طرفین به رابطه زیر میرسیم:
$$\large \frac{1}{L_T}=\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3}\ldots$$
این رابطه زمانی صحیح است که هیچ خودالقایی متقابلی بین القاگرها وجود نداشته باشد و القاگرها به صورت موازی به یکدیگر متصل باشند. این رابطه برای دو القاگر که به صورت موازی به یکدیگر متصل هستند به شکل زیر به دست میآید:
$$\large \mathrm{L}_{T}=\left(\mathrm{L}_{1} \times \mathrm{L}_{2}\right) /\left(\mathrm{L}_{1}+\mathrm{L}_{2}\right)$$
برای مطالعه بیشتر در مورد سلف یا القاگر مطلب سلف یا القاگر چیست؟ را مطالعه کنید. در انتهای این مطلب چند مدار پیچیده را که ترکیبی از مدار سری و موازی است را برای درک بهتر مفاهیم گفته شده بررسی میکنیم.
تحلیل یک مدار الکتریکی سری و موازی
در مدار زیر که مقاومتها به صورت ترکیبی از سری و موازی قرار گرفتهاند، مقاومت معادل را محاسبه کنید.
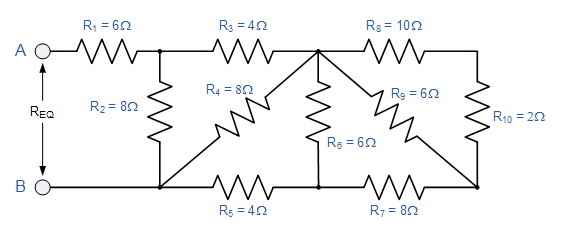
در نگاه اول ممکن است این مدار و تحلیل آن بسیار پیچیده به نظر برسد، اما همواره در ذهن خود این موضوع را یادآوری کنید که اتصال اجزای الکتریکی یک مدار از دو حالت سری یا موازی خارج نیست. از سمت راست مدار بالا شروع کنید. در همان ابتدا خواهید دید که دو مقاومت ابتدایی یعنی $$R_8$$ و $$R_{10}$$ در حالت سری با یکدیگر اتصال دارند و مقاومت معادل برای این دو ۱۲ اهم است.
این دو مقاومت با $$R_9$$ اتصال موازی دارند و بدین ترتیب مقاومت معادل این سه مقاومت به راحتی محاسبه میشود:
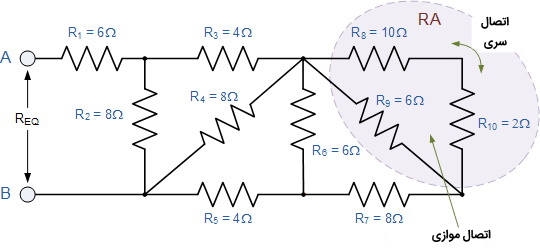
$$\large R_{A}=\frac{R_{9} \times\left(R_{8}+R_{10}\right)}{R_{9}+R_{8}+R_{10}}=\frac{6 \times(10+2)}{6+10+2}=4 \Omega$$
مقاومت معادل این سه مقاومت را $$R_A$$ مینامیم. به انشعاب جریانها دقت کنید و به راحتی میتوانید تشخیص دهید که $$R_A$$ با $$R_7$$ اتصال متوالی یا سری دارد زیرا جریان در هر دو یکی است. این در حالی است که این دو مقاومت با $$R_6$$ اتصال موازی دارند زیرا جریان در نقطه متصل به $$R_6$$ انشعاب پیدا میکند و قسمتی از آن به $$R_6$$ و قسمتی دیگر به $$R_5$$ میرود در نتیجه داریم:
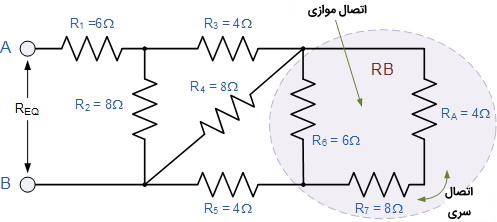
$$\large R_{B}=\frac{R_{6} \times\left(R_{A}+R_{7}\right)}{R_{6}+R_{A}+R_{7}}=\frac{6 \times(4+8)}{6+4+8}=4 \Omega$$
مقاومت معادل در این قسمت را $$R_B$$ می نامیم. مجدداً با ردگیری و انشعاب جریان میتوانید متوجه شوید که $$R_B$$ و $$R_5$$ با یکدیگر اتصال متوالی یا سری دارند ($$\mathrm{R}_{\mathrm{B}}+\mathrm{R}_{5}=4+4=8\Omega$$) و این در حالی است که با $$R_4$$ اتصال موازی دارند و داریم:
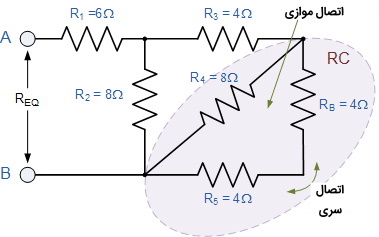
$$\large R_{C}=\frac{R_{4} \times\left(R_{B}+R_{5}\right)}{R_{4}+R_{B}+R_{5}}=\frac{8 \times(4+4)}{8+4+4}=4 \Omega$$
مقاومت معادل در این قسمت را $$R_C$$ می نامیم. مجدداً با ردگیری و انشعاب جریان میتوانید متوجه شوید که $$R_C$$ و $$R_3$$ با یکدیگر اتصال متوالی یا سری دارند و این در حالی است که با $$R_2$$ اتصال موازی دارند و داریم:
$$\large R_{D}=\frac{R_{2} \times\left(R_{C}+R_{3}\right)}{R_{2}+R_{C}+R_{3}}=\frac{8 \times(4+4)}{8+4+4}=4 \Omega$$
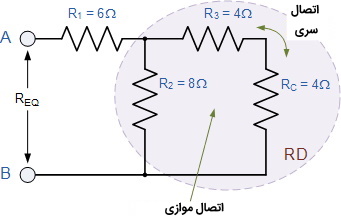
مقاومت معادل در این قسمت را $$R_D$$ می نامیم. مجدداً با ردگیری و انشعاب جریان میتوانید متوجه شوید که $$R_D$$ و $$R_1$$ با یکدیگر اتصال متوالی یا سری دارند و در نتیجه مقاومت معادل کل برابر با ۱۰ اهم به دست میآید.
در مدار ترکیبی دوم که تصویر آن در ادامه آورده شده است، مقادیر مجهول را به دست آورید.
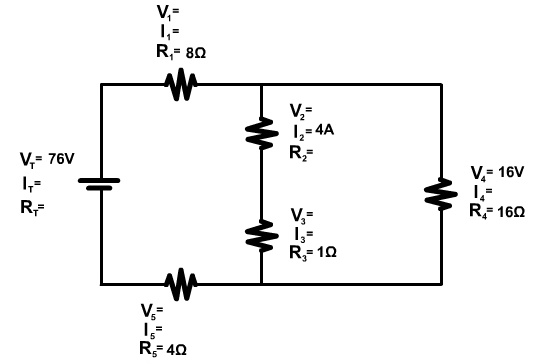
در این مدار تنها مقاومت الکتریکی و باطری داریم و به همین دلیل از قانون اهم استفاده خواهیم کرد. برای استفاده از قانون اهم به مقدار دو پارامتر از سه پارامتر جریان، ولتاژ یا مقاومت نیاز داریم. این مهم در مقاومت چهارم رخ داده است و دو پارامتر ولتاژ و مقدار مقاومت را در اختیار داریم، پس به راحتی مقدار جریان را به دست میآوریم که برابر است با:
$$\begin{array}{l}
\mathrm{V}_{4}=\left(\mathrm{l}_{4}\right)\left(\mathrm{R}_{4}\right) \\
\mathrm{I}_{4}=\left(\mathrm{V}_{4}\right) /\left(\mathrm{R}_{4}\right) \\
\mathrm{I}_{4}=(16 \mathrm{~V}) /(16 \Omega)=1 \mathrm{~A}
\end{array}$$
در مرحله بعد میتوان دید که مقاومت $$R_2$$ و $$R_3$$ با یکدیگر سری هستند پس جریان در هر دو مقاومت یکسان و برابر با ۴ آمپر است. بدین ترتیب ولتاژ دو سر مقاومت $$R_3$$ نیز قابل محاسبه است و برابر است با:
$$\begin{array}{l}
\mathrm{V}_{3}=\mathrm{I}_{3} \mathrm{R}_{3} \\
\mathrm{~V}_{3}=(4 \mathrm{~A})(1 \Omega)=4 \mathrm{~V}
\end{array}$$
نکته بعد این است که مقاومت $$R_4$$ با مقاومتهای $$R_2$$ و $$R_3$$ موازی است و بر اساس قوانین مربوط به مدار موازی افت ولتاژ دو سر اتصالات موازی با یکدیگر برابر است. با توجه به این که افت ولتاژ دو سر مقاومت $$R_4$$ ۱۶ ولت است، همین مقدار برای دو سر مقاومت $$R_2$$ و $$R_3$$ برقرار است.
با توجه به اینکه ولتاژ کل در مدار متوالی برابر با افت ولتاژ دو سر هر یک از اجزای مدار نیز است، بدین ترتیب افت ولتاژ دو سر مقاومت $$R_2$$ برابر است با:
$$V_T=V_2+V_3$$
$$16-4=12\ V$$
بدین ترتیب اختلاف پتانسیل دو سر مقاومت $$R_2$$ برابر با 12 ولت به دست میآید و با استفاده از قانون اهم مقدار مقاومت $$R_3$$ برابر است با:
$$\begin{array}{l}
\mathrm{V}_{2}=\mathrm{I}_{2} \mathrm{R}_{2} \\
\mathrm{R}_{2}=\mathrm{V}_{2} / \mathrm{l}_{2} \\
\mathrm{R}_{2}=12 \mathrm{~V} / 4 \mathrm{~A}=3 \Omega
\end{array}$$
همچنین میتوان گفت جریان کل این مدار که در شاخه مقاومت $$R_4$$ و مقاومتهای $$R_2$$ و $$R_3$$ شارش مییابد برابر با مجموع جریانهای این دو شاخه است و برابر با ۵ آمپر به دست میآید. بدین ترتیب ولتاژ دو سر مقاومت $$R_1$$ و $$R_5$$ با استفاده از قانون اهم قابل محاسبه است و داریم:
$$\begin{array}{l}
\mathrm{V}_{1}=\mathrm{I}_{1} \mathrm{R}_{1} \\
\mathrm{~V}_{1}=(5 \mathrm{~A})(8 \Omega)=40 \mathrm{~V}
\end{array}$$
$$\begin{array}{l}
\mathrm{V}_{5}=\mathrm{I}_{5} \mathrm{R}_{5} \\
\mathrm{~V}_{5}=(5 \mathrm{~A})(4 \Omega)=20 \mathrm{V}
\end{array}$$
همچنین با داشتن جریان کل، مقاومت داخلی باطری نیز توسط قانون اهم به راحتی به دست میآید:
$$\begin{array}{l}
\mathrm{V}_{\mathrm{T}}= I_{T} \mathrm{R}_{\mathrm{T}} \\
\mathrm{R}_{\mathrm{T}}=\mathrm{V}_{\mathrm{T}} / \mathrm{I}_{\mathrm{T}} \\
\mathrm{R}_{\mathrm{T}}=76 \mathrm{~V} / 5 \mathrm{~A}=15.2 \Omega
\end{array}$$
کاربرد مدار موازی
همان طور که گفتیم مدار موازی یک مدار الکتریکی است که دارای دو یا چند مسیر برای عبور بار الکتریکی است. این مدار، مدار الکتریکی استانداردی است که در بیشتر خانهها و دستگاهها یافت میشود. از آنجا که در این مدار بیش از یک راه برای عبور جریان به دستگاه فراهم میشود سیستم برق بسیار پایدارتر و کارآمدتری را ایجاد میکند. چند مورد استفاده از مدار موازی را در ادامه معرفی میکنیم.
کاربرد مدار موازی در خانهها
یافتن خانهای که از مدارهای موازی در سیمهای برق اصلی خود استفاده نکند دشوار است. به دلیل وجود مدارهای موازی میتوان برق یک دستگاه یا سیستم را روی مدار قطع کرد بدون اینکه برق لوازم دیگر قطع شود. همچنین اگر در این مدار سوء عملکرد یا اتصال کوتاه رخ دهد لزوماً کل منبع تغذیه خانه از کار نمیافتد.
کاربرد مدار موازی در زیر ساختها
مدارهای موازی یکی از اصلیترین عناصر سازنده مورد استفاده در زیرساختهای تأمین نیرو برای جمعیتهای بزرگ است. با استفاده از مدارهای موازی، مهندسان توانستهاند شبکههای قدرتی را ایجاد کنند که هم از امنیت بیشتری برخوردار باشد و هم کارآیی بالاتری داشته باشد.
بدین ترتیب زمانی که با افت جریان در قسمتی از یک مدار موازی مواجه میشویم سایر قسمتها عملکرد خود را حفظ میکنند. مدارهای موازی همچنین تأمین منبع تغذیه برابر در خانهها و ساختمانهای مختلف را آسان میکنند.
کاربرد مدار موازی در دستگاهها
از مدارهای موازی در داخل بسیاری از دستگاهها و وسایل الکتریکی استفاده میشود. دلیل اصلی استفاده از مدارهای موازی در این زمینه استفاده از بیش از یک منبع تغذیه است، مانند زمانی که بیش از یک باتری در دستگاه پرتابل استفاده میشود.
با استفاده از مدارهای موازی یک دستگاه مقدار مساوی انرژی را از منابع مختلف میگیرد و آن را در همان خط ترکیب میکند. مدارهای موازی همچنین دستگاههایی مانند چراغهای کریسمس را کاربردیتر کرده است.
مرور کلی
- ولتاژ دو سر اجزای موجود در یک مدار موازی یکسان است یعنی داریم $$V_{total}=V_1=V_2=V_3 \cdots$$
- مقاومت کل در یک مدار موازی از کوچکترین مقاومت موجود در مدار مقدار کمتری دارد و داریم: $$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\dots$$
- جریان کل در یک مدار موازی برابر است با مجموع جریانهای منفرد در دو سر هر یک از اجزای مدار یعنی: $$I_{total}=I_1+I_2+I_3+ \cdots$$
- ظرفیت کل در یک مدار موازی برابر با $$C_{\text{S}}=C_{1}+C_{2}+C_{3}+\dots$$ است.
- در اتصال موازی القاگرها، القای کل برابر با $$\frac{1}{L_T}=\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3}\ldots$$ است.
جمع بندی
در این مطلب در مورد مدارهای موازی صحبت کردیم و قوانین مربوط به ولتاژ، مقاومت، خازن، جریان و القاگر را در قرار گرفتن در یک مدار به صورت موازی مورد بررسی قرار دادیم. همچنین مداری را که ترکیبی از مدار سری و موازی بود را نیز مورد بررسی قرار دادیم و مقدار ولتاژ و جریان را برای این مدار نیز محاسبه کردیم.











با سلام. ممنونم از سایت خوبتون. 9/14.4 برابر 0/625 میشه که اشتباهاً 625 درج شده.
سلام.
آنچه در متن نوشته شده، صحیحی است. به این نکته دقت کنید که جریان برحسب میلیآمپر بوده است.
شاد باشید.