محیط مستطیل به صورت جبری — فرمول های محیط مستطیل + حل تمرین و مثال

فرمول محاسبه محیط مستطیل به صورت جبری برابر P=2l+2w یا P=2(l+w) است. این فرمولها، محیط مستطیل را بر حسب اندازه طول و عرض محاسبه میکنند. برای محاسبه محیط مستطیل بر حسب قطر، باید از یک عبارت جبری مخصوص استفاده کرد. در این آموزش، فرمولهای محیط مستطیل به صورت جبری را به همراه حل چند مثال معرفی میکنیم.
محیط مستطیل چیست؟
به اندازه مسیر دور مستطیل، محیط مستطیل میگویند. تصویر متحرک زیر، مفهوم محیط مستطیل را به خوبی نمایش میدهد.

محیط مستطیل چگونه بدست می آید؟
محیط مستطیل، از جمع اندازه تمام ضلعهای آن به دست میآید. مستطیل، یک نوع چهار ضلعی است. به همین دلیل، محیط آن به صورت زیر محاسبه میشود:
ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط مستطیل
ضلعهای مستطیل، دو به دو با هم برابر هستند. ضلعهای بزرگ با عنوان «طول» و ضلعهای کوچک با عنوان «عرض» شناخته میشوند.
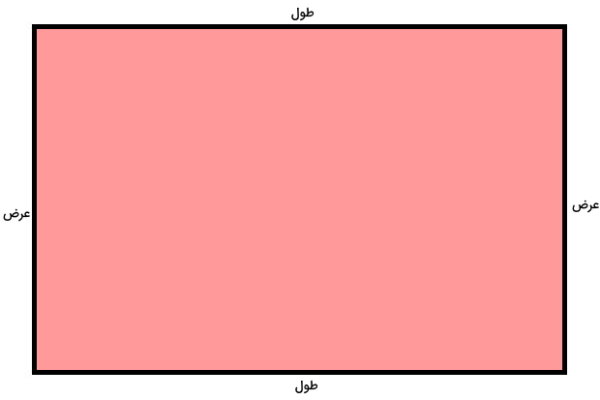
بر اساس شکل بالا، رابطه محیط مستطیل به شکل زیر درمیآید:
عرض + طول + عرض + طول = محیط مستطیل
از آنجایی که دو عرض و دو طول داریم، میتوانیم رابطه بالا را سادهسازی کنیم:
(عرض × 2) + (طول × 2) = محیط مستطیل
این رابطه، فرمول محیط مستطیل به زبان فارسی است.
محیط مستطیل به صورت جبری چگونه نوشته میشود؟
فرمول ریاضی یا عبارت جبری محیط مستطیل به صورت زیر نوشته میشود:
یا
در این فرمول، P، محیط مستطیل، l، طول مستطیل و w، عرض مستطیل را نمایش میدهد.
مثال 1: محاسبه محیط زمین فوتبال به صورت جبری
زمین فوتبال، همیشه به شکل مستطیل ساخته میشود. اگر طول یک زمین فوتبال برابر 100 متر و عرض آن برابر 65 متر باشد، اندازه دور زمین چقدر است؟

برای محاسبه اندازه دور زمین فوتبال، فرمول محیط مستطیل را مینویسیم:
- P: محیط زمین فوتبال
- l: طول زمین فوتبال برابر 100 متر
- w: عرض زمین فوتبال برابر 65 متر
اندازه طول و عرض را درون فرمول قرار میدهیم:
در نتیجه، اندازه دور زمین فوتبال برابر 330 متر است.
مثال 2: محاسبه طول مستطیل
میخواهیم با 20 چوب کبریت، مستطیلی بسازیم که بر روی هر عرض آن، 4 چوب کبریت قرار داشته باشد. تعداد چوب کبریتهای روی طول این مستطیل چقدر خواهد بود؟
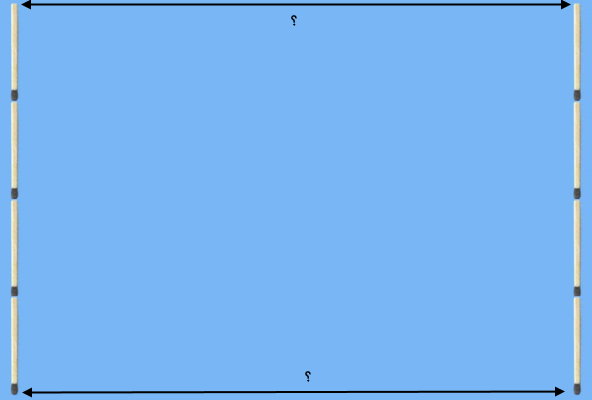
مجموع تعداد چوب کبریتها (20)، محیط مستطیل مورد نظر را نمایش میدهد. بر روی هر عرض، 4 چوب کبریت قرار دارد. این عدد، همان اندازه عرض مستطیل است. بنابراین، به منظور تعیین تعداد چوب کبریتهای مورد نیاز برای قرار دادن روی طول، فرمول محیط را مینویسیم:
- P: محیط برابر 20
- l: طول
- w: عرض برابر 4
اندازههای معلوم را درون فرمول بالا قرار میدهیم:
عبارت جبری محیط مستطیل با قطر
قطر، فاصله بین دو راس غیر مجاور (گوشههای روبهرویی) است. هر مستطیل دو قطر با اندازههای مساوی دارد.
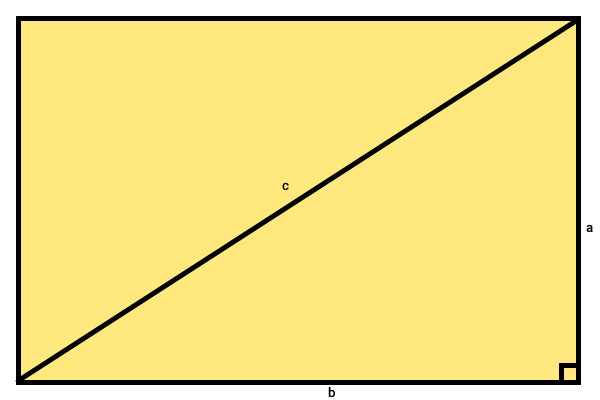
در تصویر بالا، یکی از قطرهای مستطیل را رسم کردهایم. همانطور که مشاهده میکنید، این قطر، مستطیل را به دو مثلث قائم الزاویه به وتر c و ساقهای a و b تقسیم کرده است. وتر این مثلثها با قطر مستطیل و ساقهای آنها با عرض و طول مستطیل برابر هستند. در مثلثهای قائم الزاویه، رابطه مخصوصی بین اندازه وتر و ساقها وجود دارد (قضیه فیثاغورس). این رابطه به صورت زیر نوشته میشود:
- c: وتر مثلث قائم الزاویه (قطر مستطیل)
- a: ساق اول مثلث قائم الزاویه (عرض مستطیل)
- b: ساق دوم مثلث قائم الزاویه (طول مستطیل)
اگر رابطه بالا را یک بار بر حسب a و یک بار بر حسب b بنویسیم، خواهیم داشت:
در روابط بالا، حرف d را به جای c، حرف w را به جای a و حرف l را به جای b قرار میدهیم:
به این ترتیب، اگر اندازه قطر و یکی از اندازههای طول یا عرض مستطیل را داشته باشیم، امکان محاسبه اندازه دیگر (طول یا عرض مجهول) و محیط مستطیل فراهم میشود. بر اساس این روابط، محیط مستطیل به صورت جبری و بر حسب قطر برابر است با:
یا
مثال 3: محاسبه محیط مستطیل از روی قطر
محیط مستطیلی با قطر 13 سانتیمتر و طول 12 سانتیمتر را حساب کنید. سپس، عرض آن را به دست بیاورید.
به منظور تعیین محیط مستطیل از روی قطر، فرمول مخصوص به آن (بر حسب قطر و طول) را مینویسیم:
- P: محیط مستطیل
- l: طول مستطیل برابر 12 سانتیمتر
- d: قطر مستطیل برابر 13 سانتیمتر
محیط مستطیل برابر 34 سانتیمتر است. برای به دست آوردن عرض مستطیل، فرمول ریاضی محیط مستطیل با طول عرض را مینویسیم:
- P: محیط برابر 34
- l: طول برابر 12
- w: عرض
در نتیجه، عرض مستطیل برابر 5 سانتیمتر است.
سوالات متداول در رابطه با محیط مستطیل به صورت جبری
در این بخش، به برخی از سوالات پرتکرار در رابطه با محیط مستطیل به صورت جبری به طور خلاصه پاسخ میدهیم.
تعریف محیط مستطیل چیست؟
محیط مستطیل، مجموع اندازه ضلعهای آن است.
فرمول محیط مستطیل چیست؟
فرمول محیط مستطیل برابر «جمع دو برابر طول با دو برابر عرض» است.
فرمول محیط مستطیل به صورت جبری چیست؟
عبارت جبری برای محاسبه محیط مستطیل به صورت «P=2l+2w» نوشته میشود.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش های بدست آوردن محیط و مساحت مستطیل + حل تمرین و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مستطیل چیست ؟ — تعریف و مفاهیم به زبان ساده + فیلم آموزش رایگان
- طول و عرض مستطیل چیست و چگونه بدست می آید ؟ + حل تمرین و مثال
- قطر مستطیل چیست و چه خواصی دارد؟ — فرمول های محاسبه + حل مثال
- محیط مستطیل چگونه بدست می آید؟ + فیلم آموزشی و حل تمرین و مثال
- مساحت مستطیل به زبان ساده + فیلم آموزشی و حل تمرین
- حجم مکعب مستطیل چیست ؟ — به زبان ساده + حل تمرین و مثال های متنوع
- رابطه محیط و مساحت مستطیل — معرفی فرمول ها + حل تمرین و مثال
- فرمول محیط مستطیل چیست ؟ — به زبان ساده + حل مثال
- فرمول مساحت مستطیل چیست ؟ — به زبان ساده + حل مثال
- محیط مستطیل به صورت جبری — فرمول های محیط مستطیل + حل تمرین و مثال(همین مطلب)
- مساحت مستطیل به صورت جبری — فرمول های ریاضی + حل مثال
- محیط مستطیل کسری چگونه بدست می آید ؟ + حل تمرین و مثال
- مساحت مستطیل کسری چگونه بدست می آید ؟ — حل تمرین و مثال












