مبدل دیجیتال به آنالوگ (DAC) — راهنمای جامع
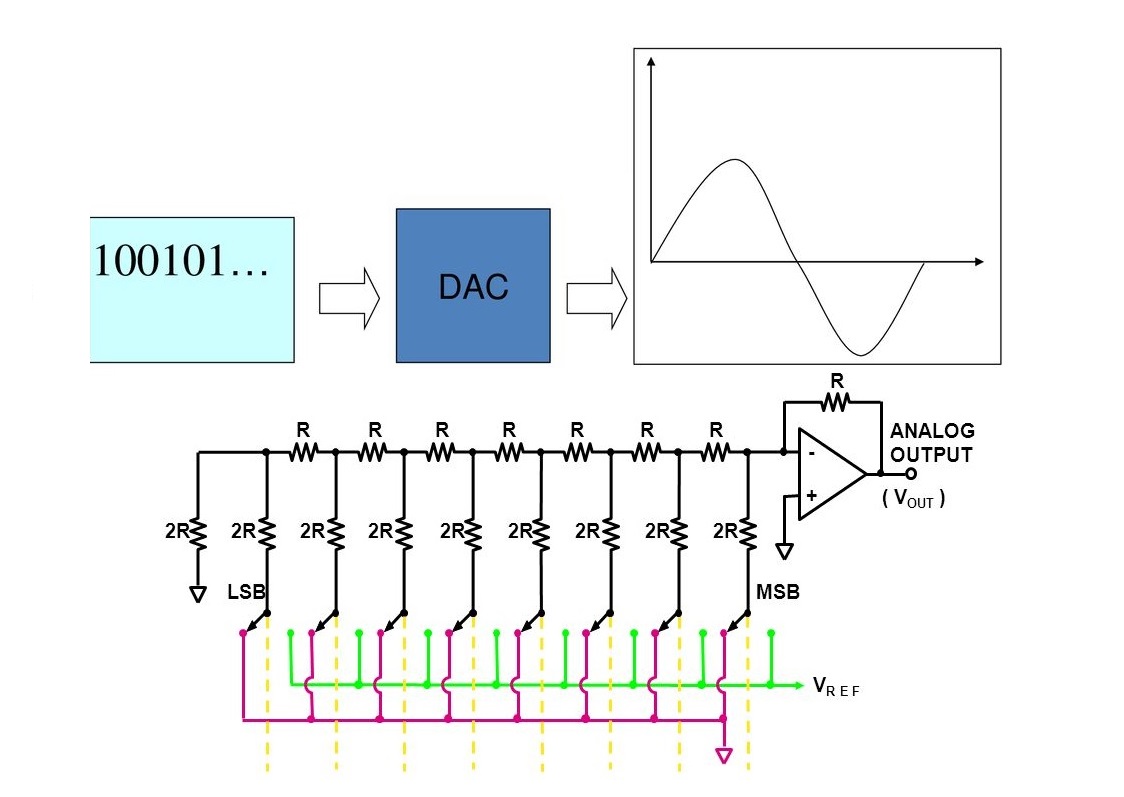
تمام مقادیر در دنیای واقعی دارای ذات آنالوگ هستند. میتوان این مقادیر را به صورت الکتریکی با سیگنالهای آنالوگ نمایش داد. یک سیگنال آنالوگ، سیگنالی متغیر با زمان است که در لحظات مختلف از زمان، میتواند هر عددی باشد. بر خلاف سیگنال آنالوگ، سیگنال دیجیتال به صورت ناگهانی از یک سطح به سطح دیگر تغییر میکند. همچنین مقادیر یک سیگنال دیجیتال فقط میتواند سطوح مشخصی باشند که تعداد این سطوح، محدود و قابل شمارش است. در این مطلب قصد داریم تا مبدل داده دیجیتال به آنالوگ یا به اختصار DAC را مورد بررسی قرار دهیم و یک نوع خاص از مبدل دیجیتال به آنالوگ که به مبدل DAC دلتا سیگما مشهور است را در محیط متلب شبیهسازی کنیم.
انواع مبدل داده
مدارات الکترونیکی که میتوانند با سیگنالهای آنالوگ کار کنند را مدارات آنالوگ میگویند. به طریق مشابه، مدار الکترونیکی که با سیگنالهای دیجیتال کار میکند، مدار دیجیتال نام دارد. یک مبدل داده (Data Converter) مداری است که اطلاعات را از یک فرم به فرم دیگر تبدیل میکند. در نتیجه میتوان گفت دو نوع مبدل داده وجود دارد:
- مبدل آنالوگ به دیجیتال (Analog to Digital Converter) یا ADC
- مبدل دیجیتال به آنالوگ (Digital to Analog Converter) یا DAC
اگر بخواهیم خروجی یک مدار آنالوگ را به عنوان ورودی، به مدار دیجیتال دیگری متصل کنیم، آنگاه باید یک مدار واسط را بین آن دو مدار قرار دهیم. این مدار واسط باید دادهها را از فرم سیگنال آنالوگ به فرم سیگنال دیجیتال تبدیل کند. چنین مداری را یک مبدل آنالوگ به دیجیتال یا به اختصار ADC مینامند.
عکس این حالت نیز صادق است، یعنی اگر بخواهیم خروجی یک مدار دیجیتال را به ورودی یک مدار آنالوگ وصل کنیم، لازم است ابتدا از مدار واسطی استفاده شود که سیگنالها را از فرمت دیجیتال به آنالوگ تبدیل کند. این مدار، مبدل دیجیتال به آنالوگ نام دارد که برای اختصار به آن مدار مبدل دیجیتال به آنالوگ میگویند. به این نکته توجه کنید که بعضی از مبدلهای آنالوگ به دیجیتال ممکن است برای عملکرد خود به یک مبدل دیجیتال به آنالوگ به عنوان یک بلوک میانی نیاز داشته باشند.
مشخصههای مدارات مبدل داده
مدارت مبدل داده معمولا دارای مشخصههای مختلفی هستند که از این میان، دو مشخصه رزولوشن (Resolution) و زمان تبدیل (Conversion Time) اهمیت فراوانی دارند.
رزولوشن
میتوان رزولوشن را به صورت زیر تعریف کرد:
رزولوشن در یک مبدل داده عبارت است از کمترین مقدار تغییراتی که در یک ولتاژ ورودی آنالوگ مورد نیاز است تا به صورت خروجی باینری یا دیجیتال نمایش داده شود. رزولوشن مبدل، به تعداد بیتهایی بستگی دارد که در خروجی مورد استفاده قرار میگیرند. در نتیجه رزولوشن را از نظر ریاضی میتوان به صورت زیر تعریف کرد:
$$ \text {Resolution} = \frac{1} {2^N} $$
در رابطه فوق، N برابر با تعداد بیتهایی است که در خروجی دیجیتال وجود دارند. با استفاده از این فرمول، میتوان مشاهده کرد که یک رابطه معکوس بین رزولوشن و تعداد بیتها وجود دارد. به این صورت که هرچه تعداد بیتها افزایش یابد، مقدار رزولوشن کاهش مییابد و بلعکس.
همچنین میتوان رزولوشن را به صورت نسبت ولتاژ ورودی آنالوگ بیشینه که میتواند به صورت باینری نمایش داده شود و عدد باینری معادل تعریف کرد. این تعریف با فرمول ریاضی زیر نشان داده میشود:
$$ \text {Resolution} = \frac{V_{FS}} {2^N -1} $$
در فرمول بالا، $$ V_{FS} $$ برابر با ولتاژ ورودی مقیاس کامل (Full Scale) یا بیشینه ولتاژ ورودی آنالوگ و $$ N $$ برابر با تعداد بیتهایی است که در خروجی دیجیتال وجود دارند.
زمان تبدیل
میزان زمانی که برای یک مبدل لازم است تا دادهها یا اطلاعات را از یک فرمت به مقدار معادل در فرمت دیگر تبدیل کند، زمان تبدیل نام دارد. چون دو نوع مبدل داده وجود دارد، بنابراین دو نوع زمان تبدیل نیز وجود دارند که عبارتند از:
- زمان تبدیل آنالوگ به دیجیتال
- زمان تبدیل دیجیتال به آنالوگ
زمانی که لازم است تا یک مبدل آنالوگ به دیجیتال یا ADC، ولتاژ ورودی آنالوگ را به مقدار خروجی دیجیتال یا باینری متناظر با آن تبدیل کند، زمان تبدیل آنالوگ به دیجیتال نام دارد. این زمان به تعداد بیتهایی بستگی دارد که در خروجی دیجیتال مورد استفاده قرار میگیرند. به طریق مشابه، میزان زمانی که لازم است تا یک مبدل دیجیتال به آنالوگ، ورودی دیجیتال یا باینری را به مقدار ولتاژ آنالوگ خروجی معادل تبدیل کند، زمان تبدیل دیجیتال به آنالوگ نام دارد. این زمان به تعداد بیتهایی بستگی دارد که در ورودی دیجیتال مورد استفاده قرار گرفتهاند.
مبدل دیجیتال به آنالوگ (DAC)
همان طور که گفتیم، یک مبدل دیجیتال به آنالوگ، سیگنال ورودی دیجیتال را به سیگنال خروجی آنالوگ تبدیل میکند. سیگنال دیجیتالی توسط کد باینری نمایش داده میشود که ترکیبی از بیتهای صفر و یک است.
بلوک دیاگرام یک مدار مبدل دیجیتال به آنالوگ در تصویر زیر نمایش داده شده است.
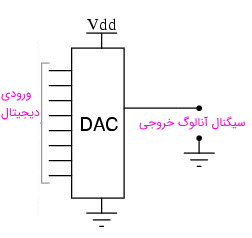
همان طور که در تصویر دیده میشود، مدار مبدل دیجیتال به آنالوگ از تعدادی ورودی باینری و یک خروجی آنالوگ تشکیل شده است. در حالت کلی، تعداد ورودیهای باینری در مبدل دیجیتال به آنالوگ، توان عدد دو هستند. بر اساس قضیه نمونه برداری نایکوئیست-شانون (Nyquist-Shannon Sampling Theorem) هر سیگنال نمونه برداری شده را میتوان زمانی به صورت ایدهآل بازسازی کرد که با نرخ نایکوئیست نمونه برداری شده باشد.
یک مدار مبدل دیجیتال به آنالوگ میتواند سیگنال نمونه برداری را با دقت بالایی مجددا به صورت یک سیگنال آنالوگ بازسازی کند. دادههای دیجیتال ممکن است از یک میکروپروسسور، مدار مجتمع مخصوص کاربردی (ASIC) و یا آرایه گیت برنامه پذیر میدانی (FPGA) تولید شوند، اما در نهایت دادهها باید به یک سیگنال آنالوگ تبدیل شوند تا بتوانند با دنیای واقعی در ارتباط باشند. اگر به یادگیری نحوه طراحی مدارات FPGA علقهمند هستید، مجموعه فیلمهای آموزش FPGA فرادرس میتواند نیازهای شما را به خوبی و به شکل کاربردی برطرف کند.
انواع مدارات مبدل دیجیتال به آنالوگ
در حالت کلی دو معماری برای مدارات مبدل دیجیتال به آنالوگ وجود دارد.
- مدار مبدل دیجیتال به آنالوگ مقاومت وزندار باینری (Binary Weighted Resistor)
- مدار مبدل دیجیتال به آنالوگ نردبانی R-2R
مدار مبدل دیجیتال به آنالوگ مقاومت وزندار باینری
مدار مبدل دیجیتال به آنالوگ مقاومت وزندار باینری، یک خروجی آنالوگ را تولید میکند که تقریبا با ورودی دیجیتال برابر و معادل است. این مبدل دیجیتال به آنالوگ، خروجی را با استفاده از مقاومتهای وزندار باینری (binary weighted resistors) در مدار جمعکننده معکوسگر (Inverting Adder Circuit) تولید میکند. وظیفه اساسی یک مبدل دیجیتال به آنالوگ، این است که ورودیها را با هم جمع کند تا در نهایت متناظر با بیتهای مختلف ورودی دیجیتال شوند. در حوزه ولتاژ یا زمانی که سیگنال ورودی به صورت ولتاژ باشد، جمع کردن بیتهای باینری میتواند با استفاده از تقویتکننده جمعکننده معکوسگر انجام پذیرد. در تصویر زیر نمایی از یک مدار مبدل دیجیتال به آنالوگ مقاومت وزندار باینری با سه مقاومت دیده میشود.
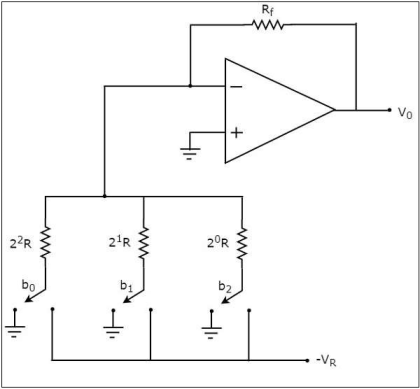
در مدار فوق، مقدار مقاومتهای ورودی به اپ امپ (Op Amp) در فرمت باینری وزندهی میشوند. زمانی که ۱ باینری دریافت شود، کلید مقاومت را به ولتاژ مرجع متصل میکند. زمانی که مدار منطقی، صفر منطقی را دریافت کند، کلید مقاومت را به زمین متصل میکند. تمام بیتهای ورودی دیجیتال به صورت همزمان به مدار مبدل دیجیتال به آنالوگ اعمال میشوند. بنابراین مدار مبدل دیجیتال به آنالوگ، خروجی آنالوگ را بر اساس ورودی دیجیتال خود تولید میکند.
میدانیم که بیتهای یک عدد باینری میتوانند فقط دو مقدار صفر یا یک داشته باشند. فرض کنید یک ورودی باینری سه بیتی به صورت $$ b_2 b_1 b_0 $$ باشد. در این حالت، بیت $$ b_0 $$ نشاندهنده بیت کم ارزش (LSB) و بیت $$ b_2 $$ نشاندهنده بیت پر ارزش (MSB) است. در کلیدهای دیجیتالی که در مدار فوق نشان داده شدهاند، اگر هر کدام از سه بیت $$ b_0 $$ و $$ b_1 $$ و $$ b_2 $$ برابر با صفر شوند، کلید متناظر با آن بیت به زمین متصل میشود و اگر برابر با یک شوند، کلید به ولتاژ منفی مرجع ($$ -V_R $$) متصل میشود.
در مدار مبدل دیجیتال به آنالوگ مقاومت وزندار باینری، ترمینال ورودی غیر معکوسکننده اپ امپ به زمین متصل شده است. این بدین معنی است که همیشه ترمینال غیر معکوسکننده اپ امپ دارای ولتاژ صفر ولت است. بر اساس مفهوم اتصال کوتاه مجازی، ولتاژ ترمینال ورودی معکوسکننده اپ امپ برابر با ولتاژ ترمینال ورودی غیر معکوسکننده آن است.
بنابراین ولتاژ در ترمینال ورودی معکوسکننده نیز برابر با صفر ولت خواهد بود. معادله جریان در گره ترمینال ورودی معکوسکننده به صورت زیر نوشته میشود:
$$ \frac{0+V_{R}b_{2}}{2^{0}R}+\frac{0+V_{R}b_{1}}{2^{1}R}+\frac{0+V_{R}b_{0}}{2^{2}R}+\frac{0-V_{0}}{R_{f}}=0 $$
$$ =>\frac{V_{0}}{R_{f}}=\frac{V_{R}b_{2}}{2^{0}R}+\frac{V_{R}b_{1}}{2^{1}R}+\frac{V_{R}b_{0}}{2^{2}R} $$
$$ =>V_{0}=\frac{V_{R}R_{f}}{R}\left \{\frac{b_{2}}{2^{0}}+\frac{b_{1}}{2^{1}}+\frac{b_{0}}{2^{2}}\right \} $$
در معادله بالا، جایگزینی $$ R=2R_{f} $$ را انجام میدهیم. در نتیجه داریم:
$$ =>V_{0}=\frac{V_{R}R_{f}}{2R_{f}}\left \{\frac{b_{2}}{2^{0}}+\frac{b_{1}}{2^{1}}+\frac{b_{0}}{2^{2}}\right \} $$
$$ =>V_{0}=\frac{V_{R}R_{f}}{2R_{f}}\left \{\frac{b_{2}}{2^{0}}+\frac{b_{1}}{2^{1}}+\frac{b_{0}}{2^{2}}\right \} $$
معادله بالا نشاندهنده معادله ولتاژ خروجی در مدار مبدل دیجیتال به آنالوگ سه بیتی با مقاومت وزندار باینری است. چون تعداد بیتها در ورودی دیجیتال مبدل دیجیتال به آنالوگ برابر با ۳ است، در نتیجه ۷ مقدار محتمل برای ولتاژ خروجی با تغییر بیتهای ورودی از ۰۰۰ تا ۱۱۱ در ولتاژ مرجع ثابت $$ V_R $$ خواهیم داشت. با توجه به معادله ولتاژ خروجی در یک مبدل دیجیتال به آنالوگ مقاومت وزندار باینری سه بیتی، میتوانیم معادله ولتاژ خروجی عمومی یک مدار مبدل دیجیتال به آنالوگ مقاومت وزندار باینری با N بیت باینری را به صورت زیر بنویسیم:
$$ =>V_{0}=\frac{V_{R}}{2}\left \{ \frac{b_{N-1}}{2^{0}}+ \frac{b_{N-2}}{2^{1}}+....+\frac{b_{0}}{2^{N-1}} \right \} $$
معایب
معایب اصلی مبدل دیجیتال به آنالوگ مقاومت وزندار باینری را میتوان به صورت زیر نام برد:
- اگر تعداد بیتهای موجود در ورودی دیجیتال مبدل دیجیتال به آنالوگ مقاومت وزندار باینری افزایش یابد، آنگاه تفاوت بین مقادیر مقاومت متعلق به بیتهای باارزش و کم ارزش نیز افزایش مییابد.
- طراحی مقاومتهای دقیقتر با افزایش بیشتر تعداد بیتها در ورودی دیجیتال، دشوارتر میشود.
مدار مبدل دیجیتال به آنالوگ نردبانی R-2R
مدار مبدل دیجیتال به آنالوگ نردبانی R-2R برای غلبه بر مشکلات مدار مبدل دیجیتال به آنالوگ مقاومت وزندار باینری مورد استفاده قرار میگیرد. همان طور که از نام این مدار مشخص است، مبدل دیجیتال به آنالوگ نردبانی R-2R از یک شبکه نردبانی R-2R در پایه معکوسکننده مدار جمعکننده استفاده میکند و بدین طریق یک خروجی آنالوگ را متناسب با ورودی دیجیتال تولید میکند. دیاگرام مداری یک مبدل دیجیتال به آنالوگ نردبانی R-2R در تصویر زیر نشان داده شده است.
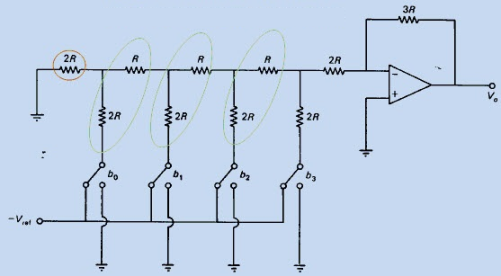
از تصویر بالا مشخص است که مدار مبدل دیجیتال به آنالوگ نردبانی مشابه با مبدل دیجیتال به آنالوگ مقاومت وزندار باینری است، با این تفاوت که در آن از ساختار آبشاری مقاومتهای R و 2R به صورت تکراری استفاده میشود. این کار باعث افزایش دقت مدار میشود؛ زیرا ایجاد مقاومتهای با مقادیر برابر و یا منابع جریان در این روش نسبتا راحتتر است. مدار تصویر فوق یک مبدل دیجیتال به آنالوگ نردبانی ۴ بیتی را نشان میدهد. برای رسیدن به دقت بالا، مقادیر مقاومتها را به صورت R و 2R انتخاب کردهایم. مقادیر باینری را به صورت $$ b_0 = 0 $$ و $$ b_1 = 0 $$ و $$ b_2 = 1 $$ و $$ b_3 = 1 $$ فرض کنید. آنگاه مدار تصویر زیر، شکل سادهشده مدار بالا را نشان میدهد.
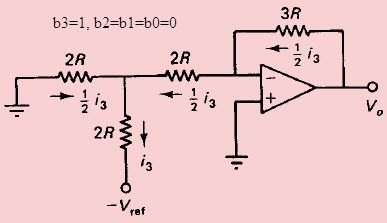
در مدار فوق، مقدار ولتاژ خروجی به صورت زیر به دست میآید:
$$ V_O = 3R (\frac {i_3} {2}) = \frac {V_{ref}} {2} $$
به طریق مشابه اگر مقادیر باینری ورودی دیجیتال در مدار مبدل دیجیتال به آنالوگ نردبانی به صورت $$ b_0 = 0 $$ و $$ b_1 = 0 $$ و $$ b_2 = 1 $$ و $$ b_3 = 0 $$ فرض شوند، آنگاه مدار به صورت شکل زیر سادهسازی میشود.
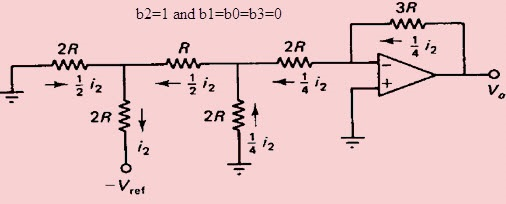
در مدار تصویر فوق، معادله خروجی به صورت زیر به دست میآید:
$$ V_O = 3R (\frac {i_2} {4}) = \frac {V_{ref}} {4} $$
حال مقادیر باینری ورودی را به صورت $$ b_0 = 0 $$ و $$ b_1 = 1 $$ و $$ b_2 = 0 $$ و $$ b_3 = 0 $$ در نظر بگیرید.
در این حالت نیز شکل ساده مدار به صورت زیر خواهد بود.
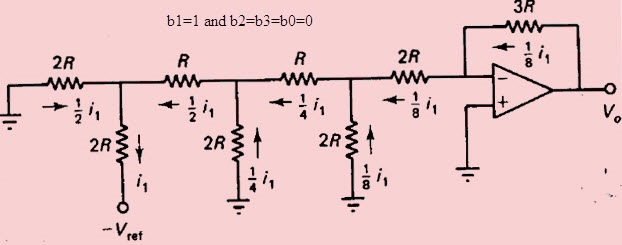
معادله ولتاژ خروجی نیز برابر است با:
$$ V_O = 3R (\frac {i_1} {8}) = \frac {V_{ref}} {8} $$
در نهایت، مدار معادل حالتی که ورودیها به صورت $$ b_0 = 1 $$ و $$ b_1 = 0 $$ و $$ b_2 = 0 $$ و $$ b_3 = 0 $$ باشند در شکل زیر نشان داده شده است.
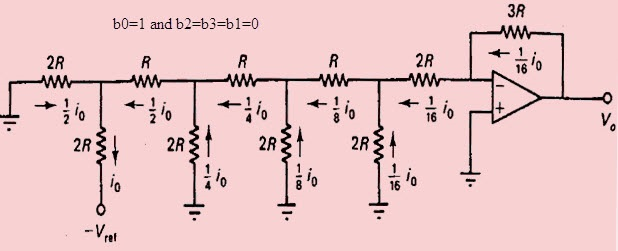
مقدار ولتاژ خروجی این مبدل برابر است با:
$$ V_O = 3R (\frac {i_0} {16}) = \frac {V_{ref}} {16} $$
بنابراین، با استفاده از معادلات بالا میتوان نتیجه گرفت که اگر دادههای ورودی دیجیتال به صورت $$ b_3 b_2 b_1 b_0 $$ باشند، آنگاه معادله ولتاژ خروجی به صورت زیر نوشته میشود:
$$ \begin{aligned} V_{0} &=\left(\frac{1}{2} b_{3}+\frac{1}{4} b_{2}+\frac{1}{8} b_{1}+\frac{1}{16} b_{0}\right) V_{\text {ref }} \\ &=\frac{1}{2}\left(b_{3}+\frac{1}{2} b_{2}+\frac{1}{4} b_{1}+\frac{1}{8} b_{0}\right) V_{\text {ref }} \end{aligned} $$
مزیت مبدل DAC نردبانی R-2R
در حالت کلی میتوان گفت که مبدل نردبانی دارای دو مزیت نسبت به مبدل مقاومت وزندار باینری است.
- مدار مبدل دیجیتال به آنالوگ نردبانی فقط شامل دو مقدار مقاومت R و 2R است. بنابراین طراحی و ساخت مدارات DAC آسانتر و دقیقتر خواهد بود.
- اگر تعداد بیتهای دیجیتال در ورودی مبدل DAC افزایش یابند، آنگاه باید تعداد کافی بخشهای R-2R به مدار اضافه کنیم.
به دلیل این ویژگیها، مدار مبدل DAC نردبانی نسبت به مدار مبدل مقاومت وزندار باینری ارجحیت بیشتری دارد.
مثال از مدار مبدل دیجیتال به آنالوگ
در این بخش میخواهیم یک مثال از مدار DAC نردبانی R-2R را بررسی کنیم.
فرض کنید ورودی دیجیتال یک مدار مبدل دیجیتال به آنالوگ نردبانی R-2R به صورت $$ b_2 b_1 b_0 = 100 $$ باشد. دیاگرام مداری آن را ترسیم کنید و سپس مدار ساده شده را به دست آورید.
حل
در تصویر زیر دیاگرام مداری یک مبدل دیجیتال به آنالوگ نردبانی سه بیتی که ورودیهای دیجیتال آن برابر با $$ b_2 b_1 b_0 = 100 $$ باشند، در تصویر زیر رسم شده است.
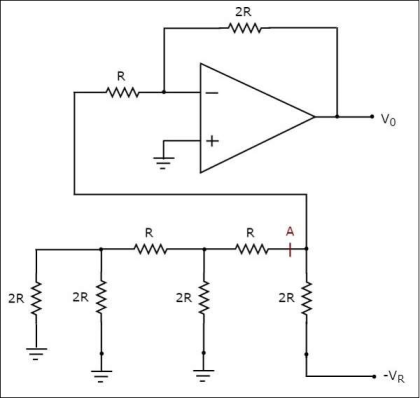
در مدار فوق، ترکیب سری و موازی از مقاومتها در سمت چپ نقطه A نسبت به زمین وجود دارند. تمام این شبکه مقاومتی را میتوان با یک مقاومت معادل $$ 2R \Omega $$ جایگزین کرد. مدار معادل ساده شده در این حالت در تصویر زیر رسم شده است.
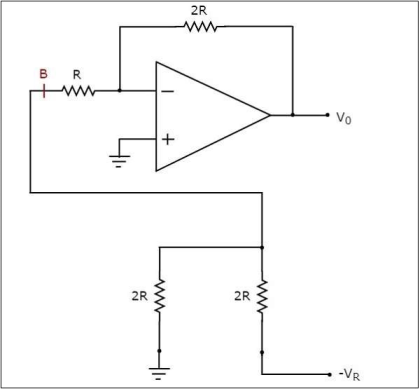
میتوانیم بخشی از شبکه را که در به سمت چپ نقطه B متصل شده است، نسبت به زمین با استفاده از مدار معادل تونن مجددا سادهسازی کنیم. دیاگرام مدار اصلاح شده در تصویر زیر رسم شده است.
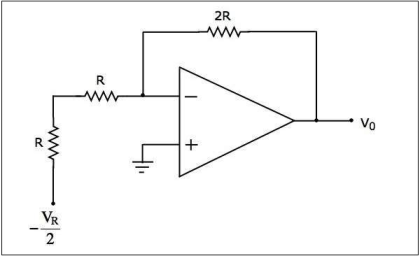
در مدار بالا، یک ترکیب سری از ۲ مقاومت وجود دارد. این دو مقاومت را نیز با یک مقاومت معادل جایگزین میکنیم. دیاگرام مدار نهایی بعد از سادهسازی در تصویر زیر رسم شده است.

حال دیاگرام مدار فوق مشابه با یک تقویتکننده معکوس کننده عمل میکند. این مدار تقویتکننده دارای ولتاژ ورودی $$ - \frac {V_R} {2} $$، مقاومت ورودی $$ 2R \Omega $$ و مقاومت فیدبک $$ 2R \Omega $$ است. مقدار ولتاژ خروجی مدار نیز به صورت زیر محاسبه میشود:
$$ V_{0}=-\frac{2R}{2R}\left(-\frac{V_{R}}{2}\right) $$
$$ V_{0}=\frac{V_{R}}{2} $$
بنابراین، ولتاژ خروجی در این مبدل دیجیتال به آنالوگ برابر با $$ \frac{V_{R}}{2} $$ ولت برای ورودی باینری $$ b_2 b_1 b_0 = 100 $$ به دست میآید.
کاربردهای مدار مبدل دیجیتال به آنالوگ
مدارات مبدل دیجیتال به آنالوگ در بسیاری از کاربردهای پردازش سیگنال و مدارات دیجیتال دیگر مورد استفاده قرار میگیرد. تعدادی از کاربردها عبارتند از:
تقویتکنندههای صوتی
مدار مبدل دیجیتال به آنالوگ برای تولید بهره ولتاژ DC با دستورات میکروکنترلر مورد استفاده قرار میگیرد. معمولا مدار مبدل دیجیتال به آنالوگ با یک مدار کدک (Codec) صوتی کامل که شامل مشخصههای پردازش سیگنال است، ترکیب میشود.
انکودر ویدئویی
یک سیستم انکودر ویدئویی (Video Encoder) سیگنال ویدئویی را پردازش میکند و سپس سیگنالهای دیجیتال را به مبدلهای دیجیتال به آنالوگ مختلفی ارسال میکند تا سیگنالهای ویدئویی آنالوگ در فرمتهای مختلفی تولید شوند. علاوه بر این سطح خروجی نیز بهینهسازی میشود. همانند کدکهای صوتی، این آیسیها نیز ممکن است دارای فرم مجتمع DAC باشند.
نمایشگر الکترونیکی
کنترلکننده گرافیکی معمولا از یک جدول جستوجو (Lookup Table) برای تولید سیگنالهای داده استفاده میکند که این سیگنالها به یک DAC ویدئویی با خروجی آنالوگ ارسال میشوند. خروجی آنالوگ مانند سیگنالهای آبی، قرمز و سبز برای داریو یک نمایشگر مورد استفاده قرار میگیرد.
سیستمهای نمونهبردار داده
دادههایی که باید مورد اندازهگیری قرار گیرند، ابتدا باید توسط یک مبدل آنالوگ به دیجیتال یا ADC به دادههای دیجیتال تبدیل شوند. سپس دادههای نمونه برداریشده به یک میکروپروسسور ارسال میشوند. سیستم نمونهبردار داده (Data Acquisition Systems) همچنین شامل یک پایانه کنترل فرایند است که در آن میکروپروسسور دادههای فیدبک را به DAC ارسال میکند تا به سیگنال آنالوگ تبدیل شوند.
کالیبراسیون
مدار مبدل دیجیتال به آنالوگ قادر است که کالیبراسون (Calibration) متغیری را برای آفست ولتاژ و بهره انجام دهد تا سیستمهای اندازهگیری و تست دارای دقت بالایی باشند.
کنترل موتور
بسیاری از الگوریتمهای کنترل موتور به سیگنالهای کنترل ولتاژ نیاز دارند. یک مدار مبدل دیجیتال به آنالوگ برای این منظور بسیار ایدهآل محسوب میشود. مدار مبدل DAC ممکن است توسط یک پردازنده یا کنترلکننده درایو شود. در تصویر زیر نمایی از کاربرد یک مدار DAC در کنترل موتور نشان داده شده است.

سیستم توزیع داده (Data Distribution System)
بسیاری از خطوط تولید کارخانجات و صنایع به چندین منبع ولتاژ قابل برنامهریزی نیاز دارند. برای این هدف لازم است که از یک بانک از مبدلهای دیجیتال به آنالوگ استفاده شود که در یکدیگر ضرب شدهاند. استفاده از DAC در طول عملکرد سیستم این امکان را فراهم میکند که ولتاژ به صورت دینامیکی تغییر کند.
پتانسیومتر دیجیتالی
تقریبا تمام پتانسیومترهای دیجیتالی بر پایه معماری DAC رشتهای کار میکنند. در واقع با استفاده از بازآرایی (Reorganization) آرایههای کلیدی یا مقاومتی و افزودن یک واسط مناسب I2C، میتوان یک پتانسیومتر دیجیتالی را پیادهسازی کرد.
رادیو نرمافزاری
در مدارت ترکیبکننده (Mixer) از یک مبدل DAC به همراه یک پردازنده سیگنال دیجیتالی یا DSP استفاده میشود تا سیگنال دیجیتال به سیگنال آنالوگ تبدیل شود. سیگنال دیجیتال در مدار ترکیبکننده منتقل و سپس به تقویتکننده توان رادیو و ترانسمیتر فرستاده میشود.
مبدل دیجیتال به آنالوگ دلتا سیگما چند بیتی در متلب
مبدل آنالوگ به دیجیتال (ADC) یا مبدل دیجیتال به آنالوگ دلتا سیگما چند بیتی (Multi Bit Delta Sigma Digital to Analog Converter) همیشه از یک مدولاتور (Modulator) دلتا سیگما چند بیتی تشکیل میشود که بیتهای داده و فیلتر پایینگذر را ایجاد میکند. اگر منبع سیگنال دیجیتال دادهها را تولید کند، آنگاه مدولاتور با استفاده از تکنولوژی دیجیتال پیادهسازی میشود و اگر منبع سیگنال آنالوگ دادهها را تولید کند، تکنولوژی ساخت مدولاتور آنالوگ خواهد بود.
همین قانون برای فیلتر پایین گذر نیز وجود دارد. دلیل نیاز به فیلتر پایین گذر در خروجی این است که باید سطح میانگین سیگنال داده را به دست آورد. میتوان دادهها را به صورت یک سیگنال با فرکانس پایین در نظر گرفت که نویزهای فرکانس بالا روی آن سوار هستند.
مدولاور دلتا سیگما هسته اساسی مبدل دلتا سیگما را تشکیل میدهد. این مدولاتور رشته داده (Bitstream) را تولید میکند. مقدار میانگین سطح این دادهها، سطح سیگنال ورودی را مشخص میکنند. بلوک دیاگرام یک مدولاتور دلتا سیگما مرتبه اول آنالوگ در تصویر زیر نشان داده شده است.
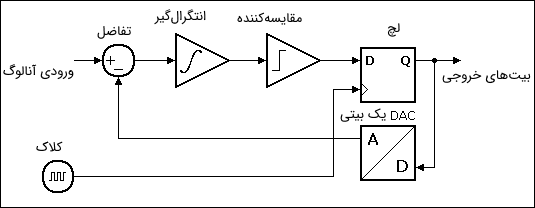
مقایسهکننده در این سیستم فقط تصمیم میگیرد که سطح آستانه چه مقدار باشد تا به ازای مقادیر ورودی بالاتر و پایینتر از آن درباره یک بیت سیگنال تکی را تولید کند. یک مدار DAC یک بیتی فقط قادر است که دو مقدار متمایز را در خروجی تولید کند.
حال اگر بخواهیم یک مبدل دیجیتال دلتا سیگما را در محیط متلب شبیهسازی کنیم، میتوانیم از مدل زیر استفاده کنیم.
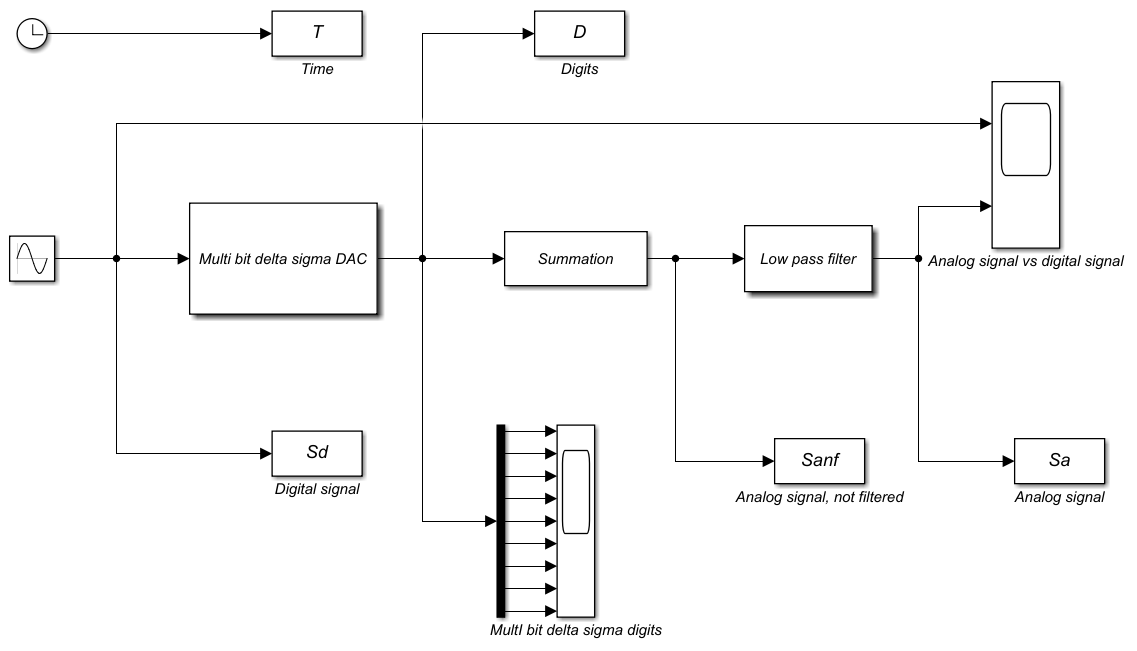
مدل سیمیولینک را میتوانید از لینک DAC دانلود کنید. همچنین کدهای مربوط به این مدل شبیهسازی در زیر آورده شدهاند.
کدهای مربوط به مقادیر اولیه
این کدها را با نام DAC_InitFcn.m ذخیره کرده و همراه با DAC.mdl در یک پوشه قرار میدهیم.
1function [sys,x0,str,ts] = DAC_SubFunction(t,x,u,flag)
2switch flag,
3
4 % Initialization
5 case 0, [sys,x0,str,ts] = mdlInitializeSizes();
6
7 % Update
8 case 2, sys = mdlUpdate(t,x,u);
9
10 % Output
11 case 3, sys = mdlOutputs(t,x,u);
12
13 % Terminate
14 case 9, sys = [];
15
16 % Unexpected flags
17 otherwise, DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
18
19end
20end
21% mdlInitializeSizes
22function [sys,x0,str,ts] = mdlInitializeSizes()
23sizes = simsizes;
24sizes.NumContStates = 0;
25sizes.NumDiscStates = 9;
26sizes.NumOutputs = 9;
27sizes.NumInputs = 1;
28sizes.DirFeedthrough = 1;
29sizes.NumSampleTimes = 1;
30sys = simsizes(sizes);
31x0 = ones(1,9);
32str = [];
33ts = [-1 0];
34end
35% mdlUpdate
36function sys = mdlUpdate(~,~,u)
37sys = u*ones(1,9);
38end
39% mdlOutputs
40function sys = mdlOutputs(t,~,u)
41if t == 0
42 DeltaSigma();
43end
44% Binary coding
45sys = iDAC(u);
46% PWM bit
47b = find(sys > 0 & sys <1);
48% PWM
49sys(b) = DeltaSigma(sys(b));
50end
51% iDAC
52function S = iDAC(E)
53persistent wLSB0
54if isempty(wLSB0)
55 wLSB0 = 0;
56end
57% MSB index
58NMSB = [5 4 3 2];
59% Vector of powers
60W = 2.^NMSB';
61% Normalization
62e = 32*(E/100+1);
63% Integer part
64n = floor(e);
65% MSB
66if n < 64
67 MSB = bitget(n,NMSB+1);
68else
69 MSB = [1 1 1 1];
70end
71% LSBs weight
72wLSB = e-MSB*W;
73% LSBs coding
74if sum(MSB) >= 1 && wLSB <= 1 && wLSB0 > 2
75 MSB = bitget(n-4,NMSB+1);
76 wLSB = e-MSB*W;
77end
78% Number of LSBs equal to "1"
79NLSB = floor(wLSB);
80% LSBs
81LSB = [zeros(1,4-NLSB) wLSB-NLSB ones(1,NLSB)];
82% Concatenation MSB-LSB
83S = [MSB LSB];
84% Previous LSBs weight
85wLSB0 = wLSB;
86end
87% Delta Sigma
88function s = DeltaSigma(e)
89persistent Sigma s0
90if ~nargin
91 Sigma = [];
92 return
93end
94if isempty(Sigma)
95 Sigma = 0;
96 s0 = 0;
97end
98Delta = e - s0;
99Sigma = Sigma + Delta;
100s = ge(Sigma+2*eps,1);
101s0 = s;
102endکدهای مربوط به تنظیمات رسم
این کدها را با نام DAC_StopFcn.m در پوشه برنامه ذخیره میکنیم.
1Figure = figure('color','w','numbertitle','off');
2% Signals
3A(1) = subplot(2,1,1);
4hold('on');
5plot(T,Sd,'b');
6plot(T,Sanf,'color',0.9*[1 1 1]);
7plot(T,Sa,'g');
8legend({'Digital signal','Analog signal (not filtered)','Analog signal (filtered)'});
9xlabel('Time [s]');
10ylabel('Magnitude [%]');
11title('Digital and analog signals','Fontsize',12,'Fontweight','light');
12box('on');
13% Digits
14A(2) = subplot(2,1,2);
15delta = repmat(0:2:2*(9-1),size(D,1),1);
16plot(T,fliplr(D)+delta,'b');
17box('on');
18A(2).YTick = 0:2:2*(9-1);
19A(2).YTickLabel = arrayfun(@(x)sprintf('b_%u',x),0:8,'UniformOutput',0);
20xlabel('Time [s]');
21ylabel('Bit value');
22title('Delta sigma digits','Fontsize',12,'Fontweight','light');
23linkaxes(A,'x');
24drawnow;
25warning('off','all');
26jFrame = get(Figure,'JavaFrame');
27jFrame.setMaximized(true);
28warning('on','all');کدهای مربوط به مدولاتور دلتا سیگما
این کدها را با نام DAC_SubFunction.m در پوشه برنامه ذخیره میکنیم.
1function [sys,x0,str,ts] = DAC_SubFunction(t,x,u,flag)
2switch flag,
3
4 % Initialization
5 case 0, [sys,x0,str,ts] = mdlInitializeSizes();
6
7 % Update
8 case 2, sys = mdlUpdate(t,x,u);
9
10 % Output
11 case 3, sys = mdlOutputs(t,x,u);
12
13 % Terminate
14 case 9, sys = [];
15
16 % Unexpected flags
17 otherwise, DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
18
19end
20end
21% mdlInitializeSizes
22function [sys,x0,str,ts] = mdlInitializeSizes()
23sizes = simsizes;
24sizes.NumContStates = 0;
25sizes.NumDiscStates = 9;
26sizes.NumOutputs = 9;
27sizes.NumInputs = 1;
28sizes.DirFeedthrough = 1;
29sizes.NumSampleTimes = 1;
30sys = simsizes(sizes);
31x0 = ones(1,9);
32str = [];
33ts = [-1 0];
34end
35% mdlUpdate
36function sys = mdlUpdate(~,~,u)
37sys = u*ones(1,9);
38end
39% mdlOutputs
40function sys = mdlOutputs(t,~,u)
41if t == 0
42 DeltaSigma();
43end
44% Binary coding
45sys = iDAC(u);
46% PWM bit
47b = find(sys > 0 & sys <1);
48% PWM
49sys(b) = DeltaSigma(sys(b));
50end
51% iDAC
52function S = iDAC(E)
53persistent wLSB0
54if isempty(wLSB0)
55 wLSB0 = 0;
56end
57% MSB index
58NMSB = [5 4 3 2];
59% Vector of powers
60W = 2.^NMSB';
61% Normalization
62e = 32*(E/100+1);
63% Integer part
64n = floor(e);
65% MSB
66if n < 64
67 MSB = bitget(n,NMSB+1);
68else
69 MSB = [1 1 1 1];
70end
71% LSBs weight
72wLSB = e-MSB*W;
73% LSBs coding
74if sum(MSB) >= 1 && wLSB <= 1 && wLSB0 > 2
75 MSB = bitget(n-4,NMSB+1);
76 wLSB = e-MSB*W;
77end
78% Number of LSBs equal to "1"
79NLSB = floor(wLSB);
80% LSBs
81LSB = [zeros(1,4-NLSB) wLSB-NLSB ones(1,NLSB)];
82% Concatenation MSB-LSB
83S = [MSB LSB];
84% Previous LSBs weight
85wLSB0 = wLSB;
86end
87% Delta Sigma
88function s = DeltaSigma(e)
89persistent Sigma s0
90if ~nargin
91 Sigma = [];
92 return
93end
94if isempty(Sigma)
95 Sigma = 0;
96 s0 = 0;
97end
98Delta = e - s0;
99Sigma = Sigma + Delta;
100s = ge(Sigma+2*eps,1);
101s0 = s;
102endدر نهایت تصویر زیر در خروجی شبیهسازی ترسیم میشود.
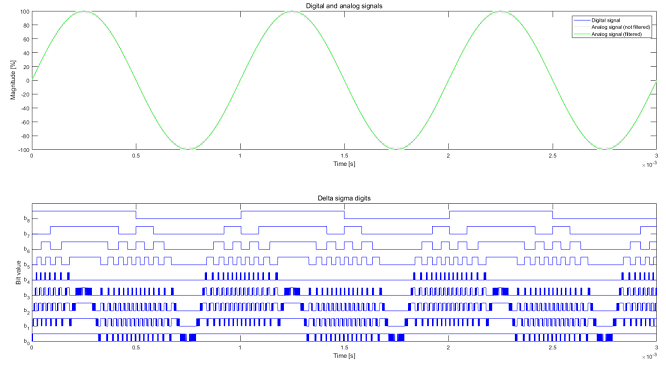
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی قدرت
- آموزش مبانی الکترونیک دیجیتال – بخش دوم
- مجموعه آموزشهای پردازش سیگنال
- آموزش تجزیه و تحلیل سیگنال ها و سیستم ها
- مدولاسیون دامنه — از صفر تا صد
- دمدولاسیون دامنه — از صفر تا صد
- انرژی و توان سیگنال — از صفر تا صد
^^











باسلام…اگر امکان دارد درس مبدل های داده به طور کامل تدریس شود. باتشکر
برای بنده که به دنبال انرژی های نوین و پاک هستم خیلی مفید بود
خیلی ممنون از توضیحاتتون