قطر دایره چیست؟ – رسم و محاسبه قطر + حل تمرین و مثال

قطر دایره بلندترین پاره‌خطی است که دو نقطه روی محیط دایره را به هم وصل می‌کند. دایره، بی‌شمار قطر دارد. تمام این قطرها از مرکز دایره می‌گذرند. قطر دایره، معمولا به منظور محاسبه محیط آن مورد استفاده قرار می‌گیرد. در این آموزش از مجله فرادرس، به معرفی ویژگی‌ها، روش‌های ترسیم، کاربرد و فرمول‌های محاسبه قطر دایره به همراه حل چندین مثال متنوع و کاربردی می‌پردازیم.

قطر چیست؟

در چندضلعی‌ها، به پاره‌خط‌هایی که ضلع‌های غیر مجاور را به هم وصل می‌کنند، قطر می‌گویند. هر چه تعداد ضلع‌ها بیشتر باشد، تعداد قطرهای قابل رسم نیز بیشتر می‌شود.

البته فقط چندضلعی‌ها دارای قطر نیستند. این پاره‌خط در منحنی‌های بسته‌ای نظیر بیضی و دایره نیز وجود دارد.

دایره چیست؟

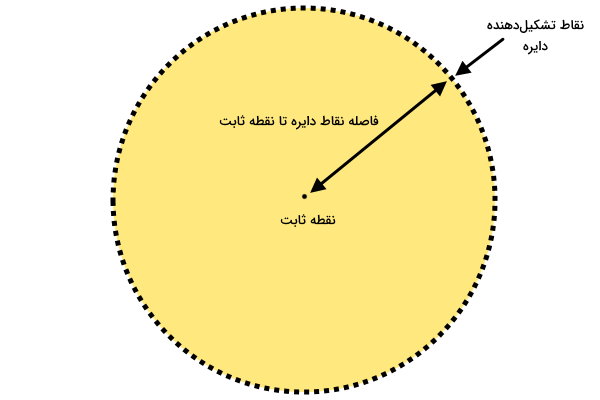
یک نقطه ثابت در صفحه و مجموعه‌ای از نقاط بهم پیوسته در اطراف آن را در نظر بگیرید. اگر فاصله این نقطه با تمام نقاط اطراف آن برابر باشد، شکلی به وجود می‌آید که با عنوان دایره شناخته می‌شود.

اجزای دایره چه هستند؟

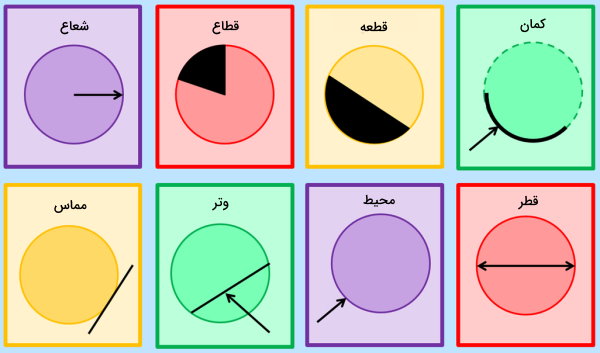
دایره، دارای اجزای متعددی است که هر یک، کاربردها و ویژگی‌های مختص به خود را دارند. از مهم‌ترین اجزای دایره می‌توان به قطر و شعاع آن اشاره کرد.

این اجزا معمولا به منظور تعیین محیط و مساحت دایره مورد استفاده قرار می‌گیرند.

قطر دایره چیست؟

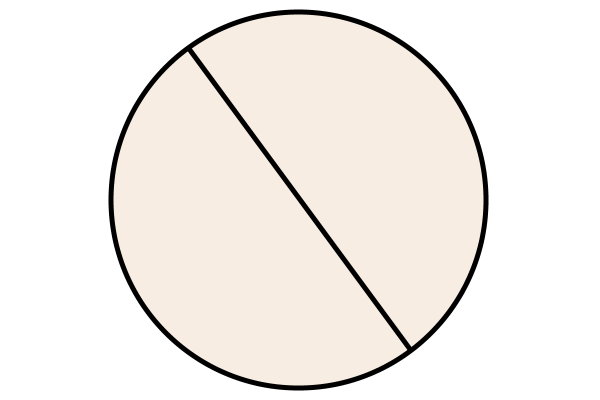
قطر دایره، پاره‌خطی است که بین دو نقطه بر روی محیط دایره رسم می‌شود و از مرکز آن عبور می‌کند. قطر، بلندترین وتر دایره محسوب می‌شود.

وتر دایره چیست و چه تفاوتی با قطر دارد؟

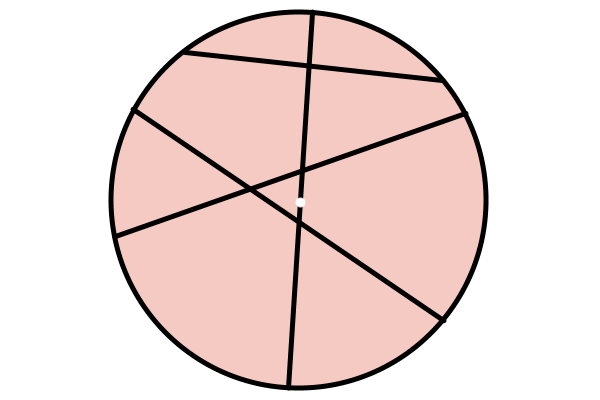
وتر، پاره‌خطی است که دو نقطه بر روی محیط دایره را به یکدیگر وصل می‌کند. تصویر زیر، چند نمونه از وترهای یک دایره را نمایش می‌دهد. یکی از این وترها (بلندترین آن‌ها)، به عنوان قطر دایره در نظر گرفته می‌شود. تفاوت قطر با دیگر وترها در این است که قطر دایره، همیشه از روی مرکز آن عبور می‌کند.

تفاوت قطر و شعاع دایره چیست؟

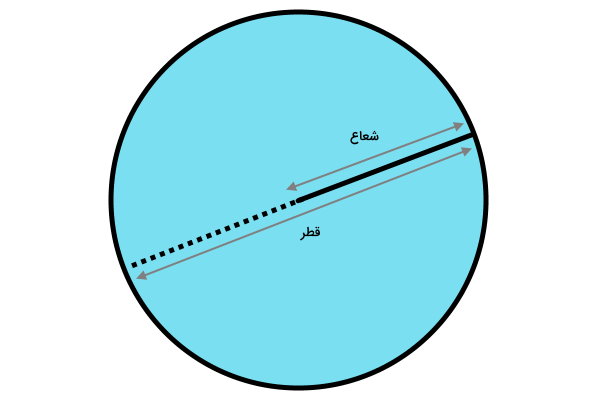
شعاع دایره، پاره‌خطی است که هر نقطه بر روی محیط دایره را به مرکز آن وصل می‌کند. اگر شعاع دایره را تا نقطه مقابل آن بر روی محیط امتداد دهیم، قطر به وجود می‌آید. به به عبارت دیگر، قطر دایره از دو شعاع تشکیل می‌شود. پس می‌توانیم بگوییم که شعاع دایره، نصف قطر آن و قطر دایره، دو برابر شعاع آن است. به طور کلی، اغلب کاربردهای قطر و شعاع دایره مشابه هستند.

خواص قطر دایره چه هستند؟

هنگام حل مسائل مرتبط با قطر دایره، ویژگی‌های زیر را در نظر داشته باشید:

• قطر، بلندترین وتر هر دایره است.
• هر قطر، دایره را به دو قسمت مساوی (دو نیم‌دایره یا دو قطاع مساوی) تقسیم می‌کند.
• مرکز قطر و مرکز دایره در یک محل قرار دارند.
• فاصله مرکز دایره تا قطر آن برابر صفر است. به عبارت دیگر، قطر دایره از روی مرکز آن عبور می‌کند.
• با رسم دو مماس از دو انتهای قطر دایره، دو خط موازی تشکیل می‌شود.
• دایره بی‌نهایت قطر دارد.

قطر نیم دایره چیست؟

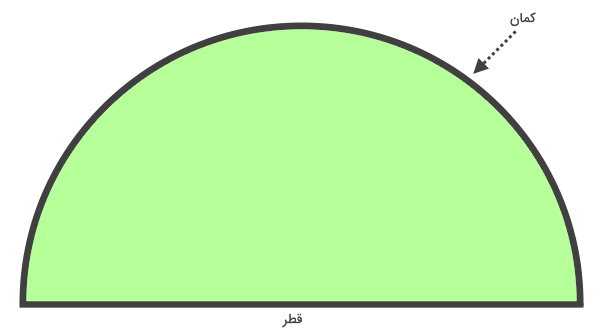
نیم‌دایره، شکلی است که از تقسیم یک دایره کامل به دو قسمت مساوی به وجود می‌آید. این شکل، از یک کمان به اندازه نصف محیط دایره و یک پاره‌‌خط تشکیل می‌شود. به پاره‌خط تشکیل‌دهنده نیم‌دایره، قطر نیم‌دایره می‌گویند. اندازه قطر نیم‌دایره برابر با اندازه قطر دایره کامل است.

قطر دایره چه کاربردی دارد؟

در مطالب پیشین مجله فرادرس در مورد محیط و مساحت دایره صحبت کردیم. قطر دایره، معمولا به منظور محاسبه محیط دایره و مساحت دایره مورد استفاده قرار می‌گیرد. البته نیم‌دایره نیز از یک قطر کامل تشکیل می‌شود. به همین دلیل، امکان محاسبه محیط نیم‌دایره (مجموع قطر و کمان) و مساحت نیم‌دایره (نصف مساحت دایره) به کمک قطر وجود دارد.

عدد پی یا نسبت محیط دایره به قطر آن

عدد پی، یک عدد ثابت و برابر 3/14 است. این عدد از تقسیم محیط دایره بر قطر آن به دست می‌آید. به عبارت دیگر، نسبت محیط دایره به قطر آن، همواره برابر 3/14 است. این نسبت، علاوه بر محاسبه محیط، در محاسبه مساحت دایره نیز به کار می‌رود. نسبت محیط دایره به شعاع آن نیز برابر با 6/28 (دو برابر عدد پی) است.

فرمول محیط دایره با قطر آن

همان‌طور که در بخش قبلی اشاره کردیم، نسبت محیط دایره به قطر آن برابر با عدد پی یا 3/14 است:

π = قطر ÷ محیط دایره

اگر نسبت بالا را بر حسب محیط بازنویسی کنیم، فرمول محیط دایره با قطر به دست می‌آید:

قطر × عدد پی = محیط دایره

قطر × ۳/14 = محیط دایره

عبارت جبری محیط دایره نیز به صورت زیر نوشته می‌شود:

$$C = \pi d$$

• C: محیط
• π: عدد پی
• d: قطر

مثال 1: محاسبه محیط تخته دارت

تخته بازی دارت، به شکل دایره است. اگر قطر این تخته حدودا برابر 50 سانتی‌متر باشد، محیط آن چقدر است؟

محیط تخته دارت توسط فرمول محیط دایره با قطر محاسبه می‌شود:

قطر × عدد پی = محیط دایره

قطر تخته دارت × 3/14 = محیط تخته دارت

50 × 3/14 = محیط تخته دارت

157 = محیط تخته دارت

در نتیجه، محیط تخته دارت برابر 157 سانتی‌متر است.

فرمول مساحت دایره با قطر آن

مساحت دایره، معمولا با استفاده از اندازه شعاع آن به دست می‌آید. فرمول مساحت دایره با شعاع برابر عبارت است از:

شعاع × شعاع × عدد پی = مساحت دایره

شعاع دایره نصف قطر آن است. پس می‌توانیم رابطه بالا را بر حسب قطر بازنویسی کنیم:

نصف قطر × نصف قطر × عدد پی = مساحت دایره

یا به عبارت ساده‌تر:

4 ÷ (قطر × قطر) × عدد پی = مساحت دایره

عبارت جبری مساحت دایره با قطر نیز به صورت زیر نوشته می‌شود:

$$A = \pi \frac {d^۲}{۴}$$

معمولا به دلیل سادگی محاسبه مساحت با شعاع، از فرمول مساحت با قطر کمتر استفاده می‌شود.

مثال 2: محاسبه مساحت میز

قطر میز دایره‌ای زیر برابر 1/5 متر است. مساحت سطح میز را حساب کنید. (عدد پی را برابر 3 در نظر بگیرید).

به منظور محاسبه اندازه سطح میز بالا می‌توانیم از فرمول مساحت دایره با شعاع یا قطر استفاده کنیم. در اینجا، فرمول مساحت با قطر را می‌نویسیم:

4 ÷ (قطر × قطر) × عدد پی = مساحت دایره

4 ÷ (1/5 × 1/5) × 3 = مساحت میز

4 ÷ (2/25) × 3 = مساحت میز

4 ÷ 6/75 = مساحت میز

1/69 = مساحت میز

مساحت میز حدودا برابر 1/69 متر مربع است.

قطر دایره چگونه رسم می شود ؟

برای یادگیری نحوه رسم قطر دایره، ابتدا باید با نحوه رسم دایره آشنا شوید. بهترین ابزار برای رسم دایره، پرگار است. پرگار، از دو بازو تشکیل می‌شود. انتهای یکی از بازوهای پرگار، یک مداد و انتهای دیگر آن، یک سوزن قرار دارد.

تصویر زیر، نحوه رسم دایره با پرگار را نمایش می‌دهد.

سوزن پرگار، بر روی مرکز دایره مورد نظر قرار داده می‌شود. پس از رسم دایره بر روی کاغذ، جای سوزن، همان مرکز دایره خواهد بود. میزان بازشدگی پرگار، شعاع دایره است.

رسم قطر دایره با خط‌کش و پرگار

برای رسم قطر دایره، به یک پرگار، خط‌کش و کاغذ نیاز داریم. در مرحله اول، دهانه پرگار را به اندازه شعاع دایره مورد نظر باز می‌کنیم. این کار، با تنظیم فاصله بین دو بازوی پرگار (دهانه پرگار) بر روی خط‌کش قابل انجام است.

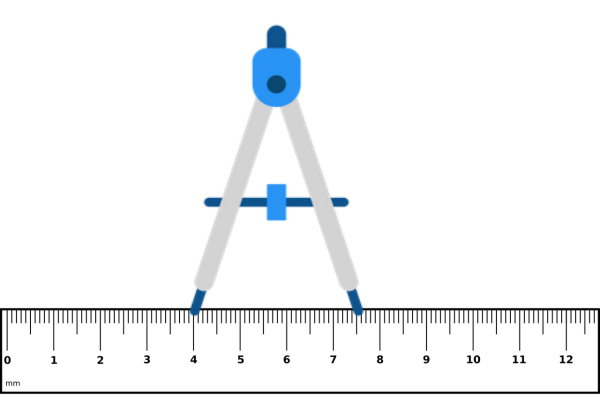
پرگار را سفت می‌کنیم و سوزن آن را بر روی نقطه مورد نظر در صفحه قرار می‌دهیم. سپس، یک دایره با شعاع تنظیم شده می‌کشیم.

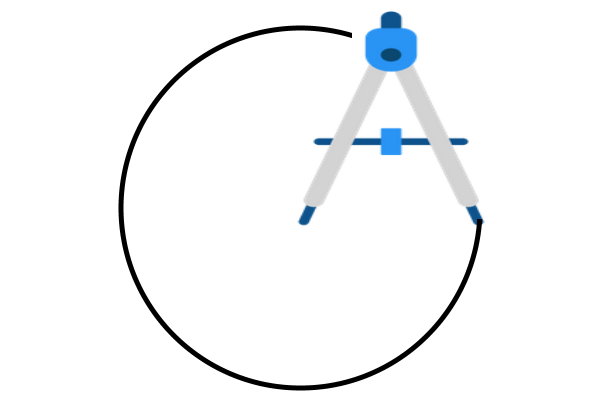
پس از رسم، دایره‌ای به شکل زیر ایجاد می‌شود. اثر سوزن بر روی کاغذ، مرکز دایره را نمایش می‌دهد.

برای رسم قطر دایره، کافی است خط‌کش خود را به گونه‌ای تنظیم کنیم که لبه آن با اثر سوزن مماس شود.

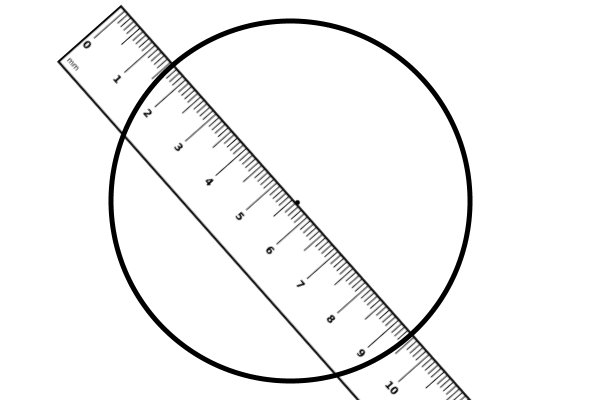
با کشیدن یک پاره‌خط بر روی لبه خط کش، قطر دایره به وجود می‌آید. اکنون خط‌کش را برمی‌داریم و قطر رسم شده را مشاهده می‌کنیم.

اکنون به سادگی می‌توانیم اندازه این پاره‌خط یا همان اندازه قطر را با خط‌کش به دست بیاوریم. به عنوان مثال، در دو تصویر قبل، یک سمت قطر بر روی عدد 1/5 خط‌کش و سمت دیگر بر روی عدد 9/5 خط‌کش منطبق بود. در نتیجه، اندازه قطر رسم شده در اینجا برابر است با:

1/5 - 9/5 = قطر دایره

8 = قطر دایره

البته از آنجایی که دایره را با شعاع مورد نظر خود رسم کردیم، برای محاسبه اندازه قطر کافی بود اندازه شعاع را دو ضرب کنیم. با این وجود، در بسیاری از مواد، شعاع دایره و مرکز آن را نداریم. در این شرایط، اندازه قطر را به کمک روش‌های دیگر اندازه می‌گیریم.

رسم قطر دایره با مرکز نامعلوم

در بخش قبلی، قطر دایره را با توجه به محل قرارگیری مرکز آن مشخص کردیم. با این وجود، اگر موقعیت مرکز دایره مشخص نباشد، باید از روش‌های غیر مستقیم برای رسم قطر استفاده کنیم. دایره زیر را نظر بگیرید.

مرکز دایره بالا معلوم نیست. اولین مرحله در پیدا کردن قطر این دایره، قرار دادن سوزن پرگار بر روی محیط آن و باز کردن دهانه پرگار به اندازه‌ای بیشتر از شعاع آن است. از آنجایی که مرکز و شعاع دایره را به طور دقیق نمی‌دانیم، پرگار را به صورت تقریبی باز می‌کنیم. در ادامه، نحوه بررسی انجام صحیح مراحل را توضیح می‌دهیم.

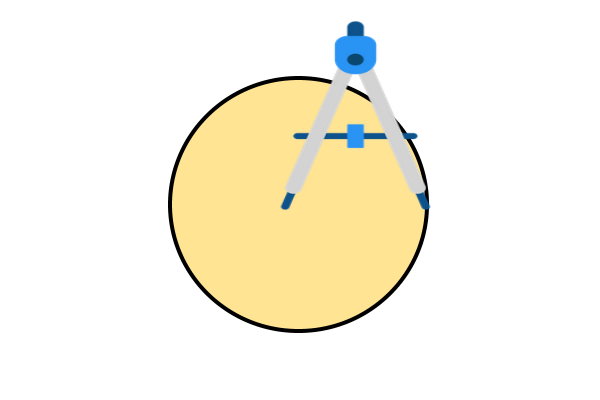
اکنون یک دایره رسم می‌کنیم.

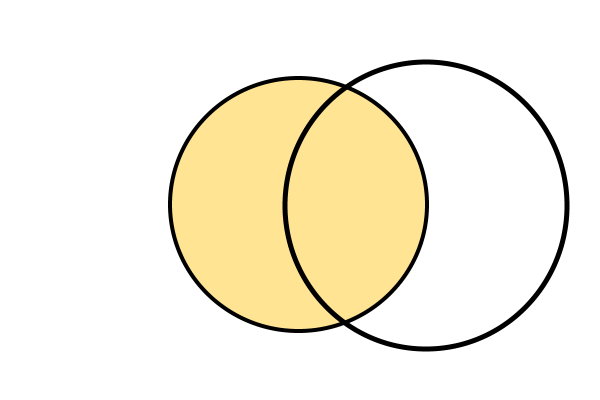
در مرحله بعد، سوزن پرگار را بر روی نقطه دیگری از محیط دایره قرار می‌دیم. سپس، بدون تغییر دادن اندازه دهانه پرگار، یک دایره دیگر رسم می‌کنیم.

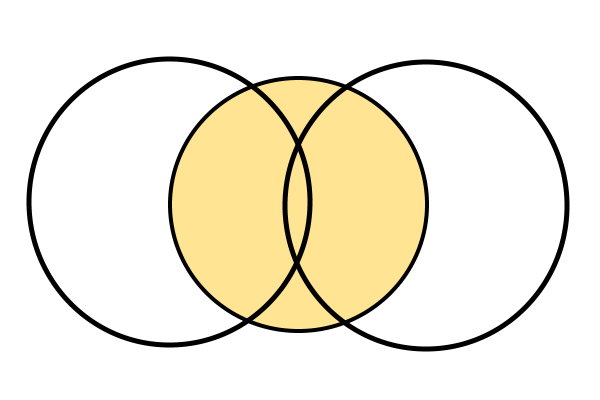
همان‌طور که مشاهده می‌کنید، دو دایره رسم شده، یکدیگر را در دو نقطه قطع می‌کنند. اگر پس از رسم دایره دوم، هیچ تقاطعی بین دو دایره به وجود نیامد، دهانه پرگار را بیشتر باز کنید و مراحل رسم دایره اول و دوم را دوباره انجام دهید. در مرحله آخر، خط‌کش را به گونه‌ای تنظیم می‌کنیم که لبه آن با دو محل تقاطع دایره‌ها مماس شود.

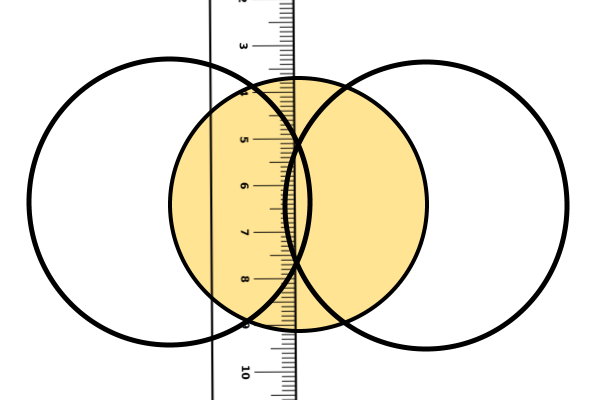
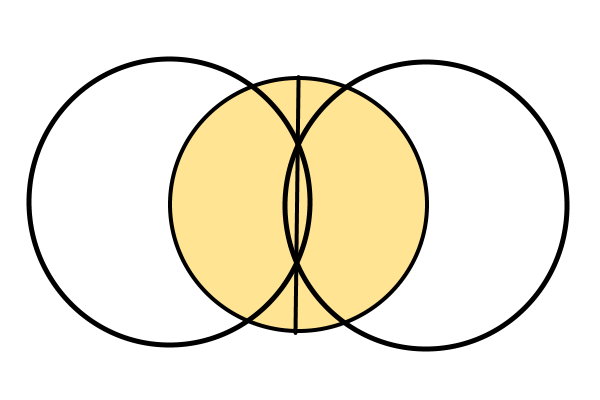
سپس، از روی محیط دایره اصلی (دایره زرد)، یک پاره‌خط تا نقطه مقابل آن بر روی محیط رسم می‌کنیم. این پاره‌خط، قطر دایره است.

حل تمرین و مثال های قطر دایره

در این بخش، به منظور درک بهتر روابط و ویژگی‌های قطر دایره، چند مثال متنوع را حل می‌کنیم.

مثال 3: محاسبه قطر دایره از روی شعاع آن

تصویر زیر، سه دایره با شعاع‌های مختلف را نمایش می‌دهد. اندازه قطر هر دایره را به دست بیاورید.

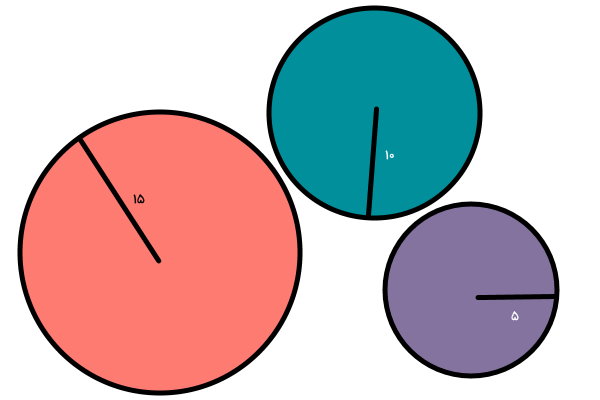
شعاع دایره، نصف قطر آن است. به همین دلیل، اگر اندازه شعاع دایره‌های بالا را در عدد 2 ضرب کنیم، قطر آن‌ها به دست می‌آید:

10 = 2 × 5 = قطر دایره بنفش

20 = 2 × 10 = قطر دایره سبز

30 = 2 × 15 = قطر دایره نارنجی

مثال 4: محاسبه قطر دایره وسط زمین فوتبال

زمین فوتبال، به شکل یک مستطیل است. محوطه مرکزی این زمین، با شکل دایره مشخص می‌شود. اگر محیط دایره وسط زمین فوتبال برابر 45 متر باشد، قطر آن چقدر خواهد بود؟ (عدد پی را برابر 3 در نظر بگیرید.)

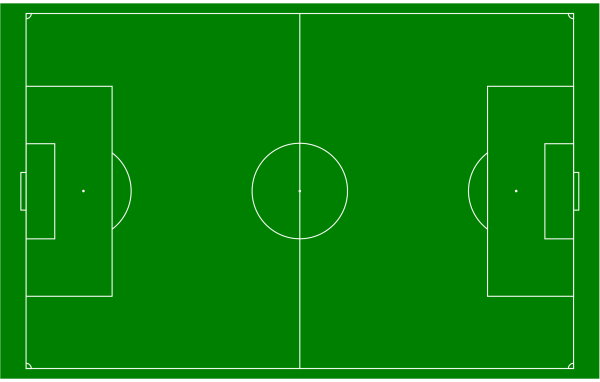
برای محاسبه قطر دایره وسط زمین فوتبال، فرمول محیط دایره با قطر را می‌نویسیم:

قطر × عدد پی = محیط دایره

قطر × 3 = 45

3 ÷ 45 = قطر

15 = قطر

در نتیجه، قطر دایره وسط زمین فوتبال برابر 15 متر است.

مثال 5: محاسبه قطر دایره از روی مساحت آن

مساحت یک دایره برابر ۲۷ سانتی‌متر مربع است. قطر آن را حساب کنید (عدد پی را برابر 3 در نظر بگیرید).

با توجه به اطلاعات مسئله، برای تعیین قطر باید از فرمول مساحت دایره استفاده کنیم:

$$A = \pi \frac {d^۲}{۴}$$

• A: مساحت دایره برابر ۲۷ سانتی‌متر مربع
• π: عدد پی برابر 3 (بر اساس فرض مسئله)
• d: قطر دایره

اندازه‌های معلوم را درون رابطه با قرار می‌دهیم و آن را بر حسب قطر حل می‌کنیم:

$$۲۷ = ۳ \frac {d^۲}{۴}$$

$$d^۲= \frac {۲۷ \times ۴}{۳}$$

$$d^۲= ۹ \times ۴$$

$$d^۲= ۳۶$$

$$d= \sqrt{۳۶}$$

$$d= ۶$$

در نتیجه، قطر دایره برابر 6 سانتی‌متر است.

مثال 6: محاسبه قطر دایره محیطی

تصویر زیر، یک مربع محاط در دایره را نمایش می‌دهد. در چندضلعی‌های محاطی، تمام گوشه‌ها بر روی محیط دایره قرار می‌گیرند. از این‌رو، به دایره دربرگیرنده آن‌ها، دایره محیطی می‌گویند. اگر مساحت مربع محاطی زیر برابر 81 میلی‌متر باشد، اندازه قطر دایره محیطی چقدر است؟

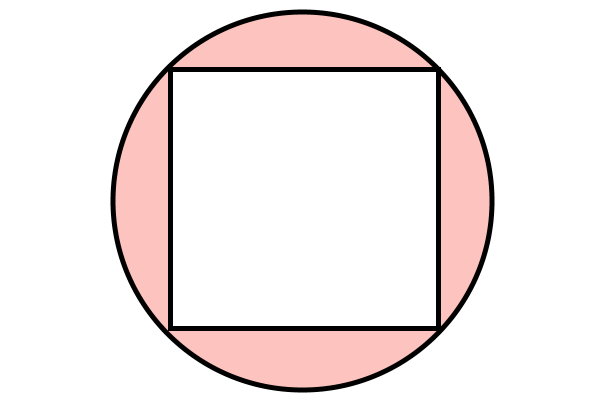
اگر مربعی در یک دایره محاط شود، اندازه قطر آن برابر با اندازه قطر دایره خواهد بود. بنابراین، در صورت تعیین قطر مربع، قطر دایره نیز به دست می‌آید. در صورت مسئله، اندازه مساحت مربع داده شده است. فرمول مساحت مربع را می‌نویسیم:

خودش × اندازه یک ضلع = مساحت مربع

$$A = a^۲$$

• A: مساحت مربع برابر 81 میلی‌متر مربع
• a: اندازه یک ضلع مربع

$$a^۲ = ۸۱$$

$$a = \sqrt {۸۱}$$

$$a = 9$$

اندازه هر ضلع مربع برابر 9 میلی‌متر است. اگر قطر مربع رسم کنیم، یک مثلث قائم الزاویه با ساق‌های 9 میلی‌متر تشکیل می‌شود.

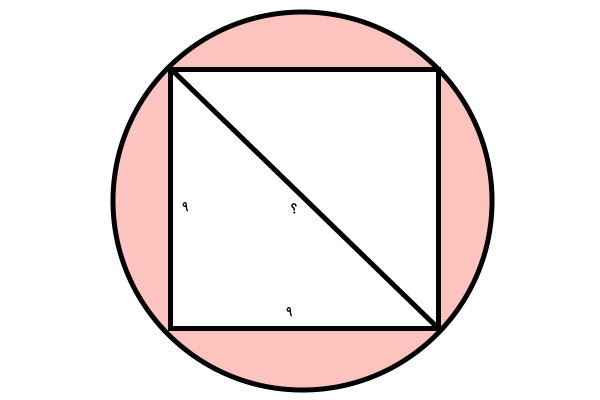
اندازه وتر مثلث قائم الزاویه (قطر مربع بالا)، از رابطه زیر به دست می‌آید:

$$c^۲=a^۲+b^۲$$

• c: وتر
• a: یکی از ساق‌ها
• b: ساق دیگر

$$c^۲=۹^۲+۹^۲$$

$$c^۲=۸۱+۸۱$$

$$c^۲=۲ \times ۸۱$$

$$c=\sqrt{۲ \times ۸۱}$$

$$c= ۹ \sqrt{۲}$$

اندازه بالا، همان قطر دایره است.

مثال 7: محاسبه قطر دایره با استفاده از خواص مماس

مماس دایره، خطی است که دایره را در یک نقطه قطع می‌کند. شعاع دایره در محل تماس بر مماس عمود است.

صویر زیر، طول یکی از مماس‌های دایره از نقطه الف تا محل تماس را نمایش می‌دهد. اگر فاصله نقطه الف تا مرکز دایره برابر 5 باشد، قطر دایره چقدر خواهد بود؟

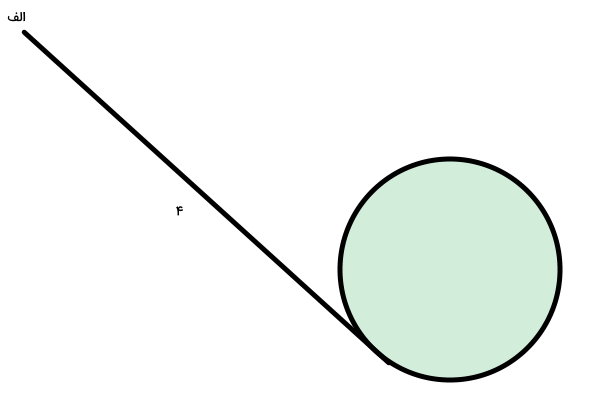
برای حل این مسئله، شعاع دایره و فاصله الف تا مرکز دایره را رسم می‌کنیم.

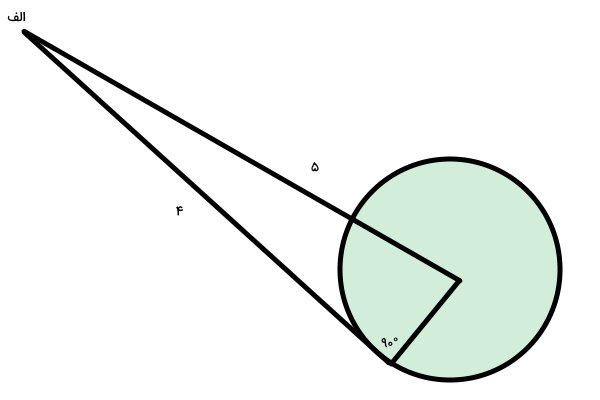
مماس دایره در محل تماس بر شعاع عمود می‌شود (تصویر بالا). در نتیجه، می‌توانیم سه ضلعی بالا را به عنوان یک مثلث قائم الزاویه در نظر بگیریم. اگر ضلع نامعلوم این مثلث را با r نمایش دهیم، بر اساس قضیه فیثاغورس خواهیم داشت:

$$۵^۲= ۴^۲ + r^۲$$

$$۲۵= ۱۶ + r^۲$$

$$r^۲ = ۲۵ - ۱۶$$

$$r^۲ = ۹$$

$$r = ۳$$

شعاع دایره برابر ۳ است. بنابراین، قطر دایره، دو برابر این اندازه، یعنی ۶ خواهد بود.

سوالات متداول در رابطه با قطر دایره

در این مطلب از مجله فرادرس فهمیدیم قطر دایره چیست و چگونه رسم می‌شود. در این بخش، به برخی از پرتکرارترین سوالات مرتبط با قطر دایره، به طور خلاصه پاسخ می‌دهیم.

دایره چند قطر دارد؟

دایره بی‌شمار قطر دارد.

شعاع دایره چند برابر قطر آن است؟

شعاع دایره، نصف قطر آن است.

آیا نیم دایره قطر دارد؟

بله. پاره‌خط تشکیل‌دهنده نیم‌دایره (قاعده نیم‌دایره)، همان قطر آن است.

بزرگ‌ترین وتر دایره چه نام دارد؟

بزرگ‌ترین وتر دایره با عنوان قطر شناخته می‌شود.

رابطه بین قطرهای دایره با یکدیگر چیست؟

تمام قطرهای دایره با یکدیگر برابر هستند.

بین قطر و شعاع دایره چه رابطه‌ای وجود دارد؟

قطر دایره، دو برابر شعاع آن است.

رابطه بین محیط و قطر دایره چیست؟

محیط دایره از ضرب قطر در عدد 3/14 به دست می‌آید.

نسبت محیط دایره به قطر آن چقدر است؟

نسبت محیط دایره به قطر آن، عدد پی یا همان 3/14 است.

آیا قطر دایره همان خط تقارن است؟

بله. اگر قطر دایره را رسم کنیم و دایره را در راستای قطر تا بزنیم، هر دو طرف قطر کاملا بر روی هم منطبق می‌شوند.

زاویه محاطی روبروی قطر دایره چند است؟

اندازه هر زاویه محاطی روبروی قطر دایره برابر 90 درجه است.