قضیه نیمساز زاویه — به زبان ساده

در آموزش‌های قبلی مجله فرادرس، با روش‌های رسم نیمساز زاویه آشنا شدیم. در این آموزش، درباره قضیه نیمساز بحث می‌کنیم. با کمک قضیه نیمساز زاویه می‌توانیم طول اضلاع نامعلوم مثلث‌ها را بیابیم، زیرا یک نیمساز زاویه، ضلع مقابلش را به دو بخش تقسیم می‌کند که متناسب با دو ضلع دیگر مثلث هستند.

نیمساز زاویه

فرض کنید مثلث دلخواه $$ABC$$ داده شده است. زوایای داخلی $$A$$، $$B$$ و $$C$$ به ترتیب در مقابل اضلاع $$a$$، $$b$$ و $$c$$ قرار دارند. اگر خطی از رأس $$A$$ رسم کنیم، به گونه‌ای که $$\angle A$$ را به دو زاویه مساوی تقسیم کرده و با ضلع $$a$$ تقاطع داشته باشد، این خط را نیمساز زاویه مثلث می‌نامیم.

فیلم آموزش هندسه ۲ – پایه یازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

مثلث شکل زیر را در نظر بگیرید. خط $$AD$$ نیمساز زاویه $$A$$ است که ضلع مقابلش، یعنی $$a$$، را به دو قسمت $$CD$$ و $$DB$$ تقسیم کرده است.

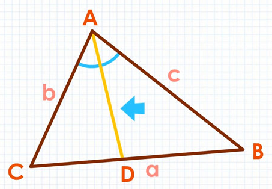
قضیه نیمساز زاویه داخلی مثلث

قضیه نیمساز زاویه بیان می‌کند که یک نیمساز زاویه در مثلث، ضلع مقابل آن را به دو بخش تقسیم می‌کند که متناسب با دو ضلع دیگر مثلث هستند.

فیلم آموزش هندسه 3 – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

در مثلث شکل بالا، نیمساز $$AD$$ ضلع $$a$$ را به دو بخش $$CD$$ و $$DB$$ تقسیم می‌کند. طبق قضیه نیمساز زاویه، این دو بخش متناسب با اضلاع $$b$$ ($$CA$$) و $$c$$ ($$BA$$) هستند.

نیمساز زاویه مثلث را به دو مثلث $$ACD$$ و $$ABD$$ تقسیم می‌کند.

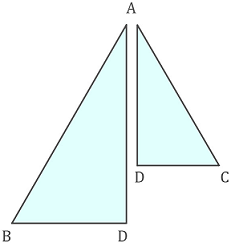
به عبارت دیگر، طبق قضیه نیمساز می‌توان نوشت:

$$\large \frac {CD}{DB} = \frac {CA} { B A }$$

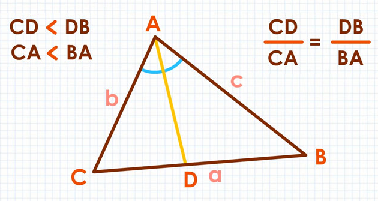
قضیه نیمساز زاویه خارجی مثلث

در آموزش‌های قبلی، با زاویه خارجی در چندضلعی‌ها آشنا شدیم و دیدیم که اگر یکی از اضلاع مثلث را به صورت خط راست ادامه دهیم، زاویه‌ای که بین این امتداد و ضلع کناری آن تشکیل می‌شود، «زاویه خارجی» (Exterior Angle) نام دارد.

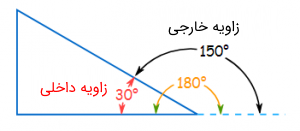
قضیه نیمساز زاویه خارجی بیان می‌کند که یک نیمساز زاویه خارجی در مثلث، ضلع خارجی مقابلش را به دو بخش تقسیم می‌کند که متناسب با دو ضلع دیگر مثلث هستند.

فیلم آموزش هندسه پایه دهم – هندسه 1 در فرادرس

کلیک کنید

مثلث زیر را در نظر بگیرید که $$AD'$$ نیمساز زاویه خارجی $$A$$ است.

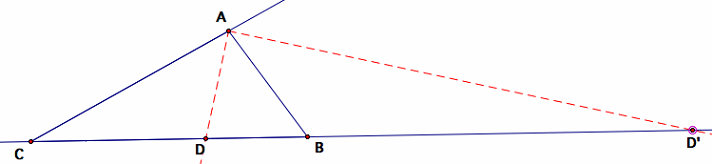
طبق قضیه نیمساز زاویه خارجی، می‌توان نوشت:

$$\large \frac { A C } { A B } = \frac {D' C } {D' B }$$

مثال‌ها

در این بخش، چند مثال را از کاربرد قضیه نیمساز بیان می‌کنیم.

مثال ۱

مثلث زیر را در نظر بگیرید. آیا خط $$AD$$ نیمساز زاویه $$A$$ است؟

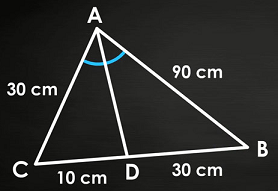
حل: نسبت اضلاع و دو بخش ضلع مقابل خط $$AD$$ را می‌نویسیم. اگر خط $$AD$$ نیمساز زاویه $$A$$ باشد، باید طبق قضیه نیمساز رابطه زیر را داشته باشیم:

$$\large \frac { CD}{DB} = \frac {CA} { B A }$$

با توجه به اندازه اضلاع مثلث بالا، داریم:‌

$$\large \frac {10}{30} = \frac {30}{90}$$

از آنجایی که تساوی مربوطه برقرار است، می‌توان گفت که خط $$A D$$ نیمساز زاویه $$A$$ است.

مثال ۲

در مثلث شکل زیر، خط $$A D$$ نیمساز زاویه $$A$$ است. اندازه ضلع $$B A$$ را به دست آورید.

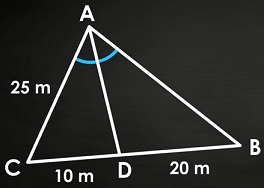
حل: اگر خط $$AD$$ نیمساز زاویه $$A$$ باشد، باید تساوی زیر را داشته باشیم:

$$\large \frac { CD}{DB} = \frac {CA} { B A }$$

با توجه به اطلاعات مثال، داریم:

$$\large \frac {10}{25} = \frac {20} { BA}$$

$$\large BA = \frac {500}{10}$$

$$\large B A = 50 \; \text{m}$$

مثال ۳

در مثلث $$\triangle { A B C }$$، داریم:

$$\large \lvert \overline { A B } \rvert = 1 0 ,\;\;\; \lvert \overline { B C } \rvert = 8 , \;\;\; \lvert \overline { A C } \rvert = 1 2$$

فرض کنید $$D$$ نقطه‌ای روی ضلع $$\overline { A B }$$ است، به گونه‌ای که خط $$\overline { C D }$$ نیمساز $$\angle C$$ باشد. طول $$\overline { A D }$$ را محاسبه کنید.

حل: فرض می‌کنیم:

$$\large  \lvert \overline { A B } \rvert = c , \;\;\; \lvert \overline { B C } \rvert = a , \;\;\; \lvert \overline { A C } \rvert = b , \;\;\; \lvert\overline{AD}\rvert=y, \;\;\; \lvert\overline { B D } \rvert = x$$

بنابراین، باید $$y$$ را پیدا کنیم. طبق قضیه نیمساز زاویه، داریم:‌

$$\large \frac { y } { b } = \frac { x } { a } \implies \frac { y } { 1 2 } = \frac { x } { 8 } .$$

از آنجایی که $$x + y = c$$ یا $$x = c - y$$، می‌توان نوشت:‌

$$\large \begin {aligned} \frac { y } { 1 2 } & = \frac { 1 0 - y } { 8 } \\ \\ \Rightarrow y & = 6 . \ \end{aligned}$$

مثال ۴

مثلثی را در نظر بگیرید که یکی از رأس‌های آن با ارتفاع، میانه و نیمساز زاویه آن رأس به چهار زاویه مساوی تقسیم شده است. اندازه زاویه رأس مورد نظر را بیابید.

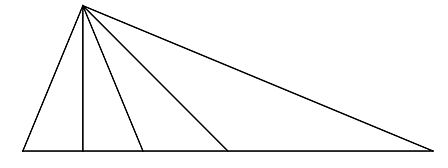
حل: قاعده مثلث به چهار بخش با نسبت $$x : x : y : 2 x + y$$ تقسیم شده است. فرض کنید طول ضلع سمت چپ مثلث برابر با ۱ باشد. آنگاه طول نیمساز زاویه نیز برابر با ۱ خواهد بود.

اکنون از قضیه نیمساز زاویه برای مثلث بزرگ استفاده می‌کنیم و می‌بینیم که طول ضلع سمت راست برابر است با:

$$\large \dfrac { 2 x + 2 y } { 2 x } = 1 + \dfrac { y } { x } .$$

حال اگر قضیه نیمساز را به مثلث سمت چپ اعمال کنیم، تساوی زیر را برای طول مشابه خواهیم داشت:

$$\large \frac { 2 x + y } { y } = 1 + \frac { 2 x } { y }$$

بنابراین، داریم:‌

$$\large \dfrac { y } { x } = \dfrac { 2 x } { y } \implies x : y = 1 : \sqrt 2 .$$

اکنون برای بار سوم از قضیه نیمساز استفاده کرده و آن را به مثلث سمت راست که از ارتفاع و میانه تشکیل شده است، اعمال می‌کنیم. بخش‌های قاعده نسبت $$x : y = 1 : \sqrt{2}$$ خواهند داشت. در نتیجه، ارتفاع و قاعده نسبت یکسانی دارند. در نهایت، نتیجه می‌گیریم این مثلث قائم‌الزاویه با زوایای $$45 ^ \circ - 4 5 ^ \circ - 9 0 ^ \circ$$ است. در نتیجه، زاویه‌ای که به چهار بخش تقسیم شده، قائمه است.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• استوانه و مفاهیم آن در هندسه — به زبان ساده
• فرمول هرون — به زبان ساده
• زاویه داخلی و محاسبات آن در اشکال چندضلعی — به زبان ساده

^^