فرمول مساحت بیضی — به زبان ساده + حل تمرین و مثال

فرمول مساحت بیضی برابر «شعاع کوچک × شعاع بزرگ × ۳/۱۴» و عبارت جبری آن برابر «S=πab» است. مساحت بیضی، سطح درون منحنی این شکل را نمایش میدهد. محاسبه اندازه این سطح، با استفاده از طول محورهای اصلی و فرعی صورت میگیرد. در این آموزش، به معرفی فرمول مساحت بیضی با محور، قطر و شعاع میپردازیم و چندین مثال کاربردی و متنوع را حل میکنیم.
مساحت بیضی چیست و چگونه بدست می آید؟
مساحت بیضی، اندازهای است که محدوده درون این شکل هندسی را نمایش میدهد. اندازه مساحت بیضی، با استفاده از شعاعهای بزرگ و کوچک به دست میآید.
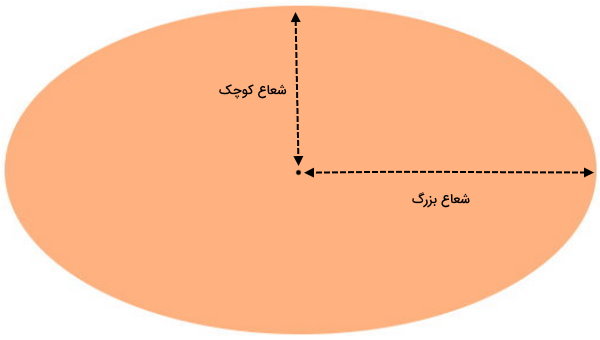
فرمول مساحت بیضی چیست؟
فرمول مساحت بیضی به صورت زیر نوشته میشود:
نصف محور فرعی × نصف محور اصلی × عدد پی = مساحت بیضی
محور اصلی، بزرگترین قطر بیضی است که با عبور از مرکز بیضی، دو نقطه مقابل بر روی محیط آن را به یکدیگر وصل میکند. کوچکترین قطر بیضی، با عنوان محور فرعی شناخته میشود. تصویر زیر، محورهای اصلی و فرعی را به همراه گوشههای آنها نمایش میدهد.
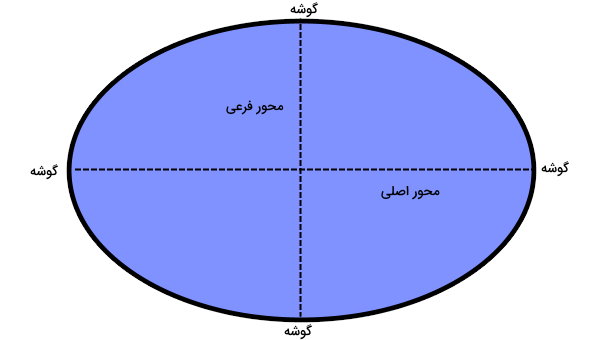
محورهای اصلی و فرعی با عنوانهای قطر بزرگ و قطر کوچک نیز شناخته میشوند. به همین دلیل، فرمول مساحت بیضی را میتوان به صورت زیر نوشت:
نصف قطر کوچک × نصف قطر بزرگ × عدد پی = مساحت بیضی
امکان محاسبه مساحت بیضی با انتگرال نیز وجود دارد.
مثال ۱: محاسبه مساحت بیضی با قطر
اندازه قطرهای کوچک و بزرگ یک بیضی به ترتیب برابر ۴۰ و ۳۰ است. مساحت بیضی را به دست بیاورید.
مساحت بیضی با استفاده از رابطه زیر محاسبه میشود:
نصف محور فرعی × نصف محور اصلی × عدد پی = مساحت بیضی
عدد پی برابر ۳/۱۴ است. نصف محور اصلی (نصف قطر بزرگ) و نصف محور فرعی (نصف قطر کوچک) نیز برابر هستند با:
۲۰ = ۲ ÷ ۴۰ = نصف محور اصلی
۱۵ = ۲ ÷ ۳۰ = نصف محور فرعی
اندازههای معلوم را درون فرمول قرار میدهیم:
۱۵ × ۲۰ × ۳/۱۴ = مساحت بیضی
۹۴۲ = مساحت بیضی
در نتیجه مساحت بیضی برابر با ۹۴۲ واحد سطح است.
فرمول مساحت بیضی با شعاع
بر اساس فرمول مساحت بیضی با قطر داریم:
نصف قطر کوچک × نصف قطر بزرگ × عدد پی = مساحت بیضی
شعاع بیضی، نصف قطر آن است. بنابراین، فرمول مساحت بیضی با شعاع به صورت زیر نوشته میشود:
شعاع کوچک × شعاع بزرگ × عدد پی = مساحت بیضی
مثال ۲: محاسبه مساحت بیضی با شعاع
شعاعهای بزرگ و کوچک یک بیضی برابر با ۴۰ و ۳۰ سانتیمتر هستند. مساحت بیضی چند است؟
مساحت بیضی با استفاده اندازههای شعاعهای آن، توسط رابطه زیر محاسبه میشود:
شعاع کوچک × شعاع بزرگ × عدد پی = مساحت بیضی
۳۰ × ۴۰ × ۳/۱۴ = مساحت بیضی
۳۷۶۸ = مساحت بیضی
در نتیجه، مساحت بیضی برابر ۳۷۶۸ سانتیمتر مربع است.
فرمول مساحت بیضی به صورت جبری
بیضی زیر را در نظر بگیرید. اندازه محور اصلی این بیضی برابر با ۲a و اندازه محور فرعی آن برابر ۲b است.
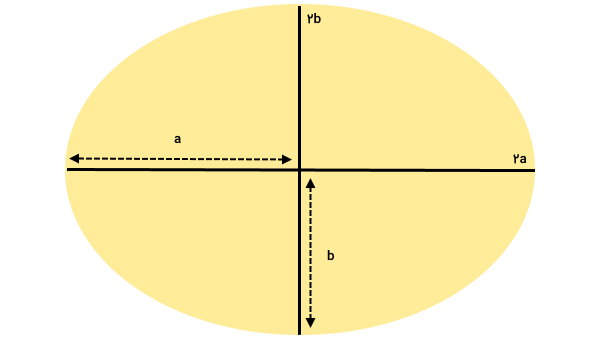
بر اساس تصویر، شعاع بزرگ بیضی برابر با a (نصف محور اصلی) و شعاع کوچک آن برابر با b (نصف محور فرعی) خواهد بود. فرمول مساحت بیضی عبارت است از:
نصف محور فرعی × نصف محور اصلی × عدد پی = مساحت بیضی
به جای نصف محورهای فرعی و اصلی، اندازه آنها (a و b) را قرار میدهیم:
a × b × عدد پی = مساحت بیضی
در ریاضیات، مساحت با حرف انگلیسی S و عدد پی، با حرف یونانی π نمایش داده میشود. به این ترتیب، میتوانیم فرمول بالا را به صورت زیر بنویسیم:
- S: مساحت بیضی
- π: عدد ثابت ۳/۱۴
- a: شعاع بزرگ بیضی (نصف محور اصلی)
- b: شعاع کوچک بیضی (نصف محور فرعی)
رابطه بالا با عنوان فرمول مساحت بیضی به صورت جبری شناخته میشود.
مثال ۳: محاسبه مساحت بیضی با عبارت جبری
کف یک ساختمان به شکل بیضی ساخته شده است. اگر قطر بزرگ بیضی برابر ۱۴ متر و قطر کوچک آن برابر ۱۰ متر باشد، مساحت کف ساختمان چقدر است؟
به منظور تعیین مساحت کف ساختمان، از فرمول مساحت بیضی استفاده میکنیم:
- S: مساحت بیضی
- π: عدد ثابت ۳/۱۴
- a: شعاع بزرگ بیضی
- b: شعاع کوچک بیضی
شعاع بزرگ و کوچک بیضی برابر هستند با:
۷ = ۲ ÷ ۱۴ = a
۵ = ۲ ÷ ۱۰ = b
این اندازهها را درون فرمول قرار میدهیم:
در نتیجه، مساحت کف ساختمان برابر ۱۰۹/۹ متر مربع است.
مثال ۴: محاسبه محور بیضی بیضی از روی مساحت
مساحت یک بیضی برابر با ۱۵۶ اینچ مربع و اندازه محور فرعی آن برابر با ۸ اینچ است. اندازه محور فرعی را با فرض ۳=π حساب کنید.
اندازه محور اصلی از روی مساحت و محور فرعی، با استفاده از فرمول زیر محاسبه میشود:
- S: مساحت بیضی برابر ۱۵۶ اینچ
- π: عدد ثابت ۳ (بر اساس فرض مسئله)
- a: شعاع بزرگ بیضی
- b: شعاع کوچک بیضی برابر با ۴ اینچ (نصف محور فرعی به اندازه ۸ اینچ)
اندازههای معلوم را درون فرمول قرار میدهیم و آن را بر حسب شعاع بزرگ (a) حل میکنیم:
شعاع بزرگ بیضی برابر ۱۳ اینچ است. بنابراین، اندازه محور اصلی آن از رابطه زیر به دست میآید:
شعاع بزرگ × ۲ = محور اصلی
۱۳ × ۲ = محور اصلی
۲۶ = محور اصلی
در نتیجه، اندازه محور اصلی بیضی برابر ۲۶ اینچ است.
مثال ۵: محاسبه مساحت بیضی از روی فاصله کانونی
فاصله مرکز یک بیضی تا یکی از کانونهای آن برابر ۴ و اندازه شعاع بزرگ بیضی برابر ۵ است. مساحت بیضی را به دست بیاورید.
مساحت بیضی، با استفاده از اندازه شعاعهای بزرگ و کوچک آن به دست میآید. در صورت سوال، فقط یکی از این اندازهها داده شده است. بین فاصله مرکز تا کانون بیضی و شعاعهای آن، رابطهای مشابه با قضیه فیثاغورس وجود دارد. این رابطه به صورت زیر نوشته میشود:
- c: فاصله مرکز تا کانون برابر ۴
- a: شعاع بزرگ برابر ۵
- b: شعاع کوچک
۴^۲ = ۵^۲ - b^۲
شعاع کوچک بیضی برابر ۳ است. اکنون میتوانیم با استفاده از این اندازه و اندازه شعاع بزرگ، مساحت بیضی را به دست بیاوریم:
- S: مساحت بیضی
- π: عدد ثابت ۳/۱۴
- a: شعاع بزرگ بیضی برابر ۵
- b: شعاع کوچک بیضی برابر با ۴
در نتیجه، مساحت بیضی برابر ۶۲/۸ واحد سطح است.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت بیضی — هر آنچه باید بدانید» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- بیضی چیست ؟ | تعریف و مفاهیم به زبان ساده
- محیط بیضی چیست ؟ — تقریبها، سریها و انتگرالها
- مساحت بیضی چیست ؟ — به زبان ساده + فیلم آموزش رایگان و حل تمرین
- مساحت بیضی با انتگرال — اثبات فرمول به زبان ساده
- قطر بیضی چیست و بیضی چند قطر دارد ؟ — به زبان ساده
- رسم بیضی — آموزش تصویری و گام به گام هفت روش — به زبان ساده
- محاسبه آنلاین مساحت بیضی — معرفی بهترین سایتها + مثال
- فرمول مساحت بیضی — به زبان ساده + حل تمرین و مثال(همین مطلب)
- محاسبه آنلاین محیط بیضی — معرفی بهترین سایتها + مثال
- فرمول محیط بیضی چیست ؟ — معرفی 9 فرمول پرکاربرد
- بیضی چند قطر دارد ؟ — تعداد ضلع، گوشه و دیگر اجزای بیضی — به زبان ساده