سیستم با ورودی تصادفی – به زبان ساده

در مطالب گذشته وبلاگ فرادرس در مورد نحوه محاسبه انتگرال کانولوشن صحبت شد. در این مطلب قصد داریم تا یکی از کاربرد‌های این انتگرال را توضیح دهیم. با استفاده از این انتگرال می‌توان سیستم خطی تغییرناپذیر نسبت به زمان را تحلیل کرد. این نوع از سیستم‌ها در آمار و البته در مهندسی کنترل کاربرد بسیاری دارند.

سیستم خطی تغییرناپذیر

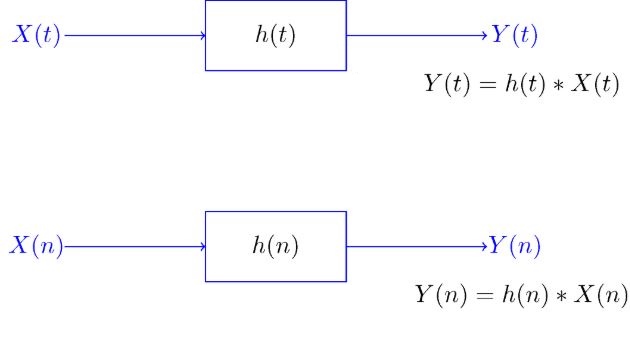
یک سیستم خطی تغییرناپذیر با زمان را می‌توان با استفاده از پاسخ ضربه‌ای آن شناسایی کرد. به‌طور دقیق‌تر فرض کنید $$X ( t )$$ سیگنال ورودی یک سیستم باشد. در این صورت خروجی سیستم یا همان $$Y ( t )$$ را می‌توان به‌صورت زیر بیان کرد:

$$\begin {align} \nonumber Y ( t ) = \int _ { - \infty } ^ { \infty } h ( \alpha ) X ( t - \alpha ) \; d \alpha = \int _ { - \infty } ^ { \infty } X ( \alpha ) h ( t - \alpha ) \; d \alpha. \end {align}$$

در ادامه شماتیک چنین سیستمی نشان داده شده است.

به انتگرال فوق اصطلاحا، کانوولوشن $$h$$ و $$X$$ گفته شده و می‌توان عبارت فوق را به‌صورت زیر نیز نشان داد.

$$\begin {align} \nonumber Y ( t ) & = h ( t ) \ast X ( t ) = X ( t ) \ast h ( t ) \end {align}$$

توجه داشته باشید که انتگرال فوق را می‌توان در حالتی که سیگنال ورودی به‌صورت یک تابع ضربه باشد، بدست آورد ($$x ( t ) = \delta ( t )$$). برای یک سیستم زمانی گسسته، خروجی را می‌توان به‌صورت زیر بیان کرد:

$$\begin {align} \nonumber Y ( t ) & = h ( t ) \ast X ( t ) = X ( t ) \ast h ( t ) \end {align}$$

تابع ضربه گسسته را می‌توان با استفاده از تابع دوضابطه‌ای زیر نیز تعریف کرد:

$$ \begin{align} \nonumber \delta(n) = \left\{ \begin{array} { l l} 1 & \quad \text {n=0} \\ & \quad \\ 0 & \quad \text {n≠0} \end {array} \right. \end {align} $$

سیستم‌های مستقل با ورودی تصادفی

سیستمی مستقل زمانی را در نظر بگیرید که پاسخ ضربه آن برابر با $$h ( t )$$ باشد. اگر $$X ( t )$$ یک ورودی تصادفی باشد، در این صورت خروجی $$Y ( t )$$ نیز تصادفی است. این خروجی را می‌توان با استفاده از تبدیل کانولوشن زیر بیان کرد:

$$\begin {align*} Y ( t ) & = h ( t ) \ast X ( t ) \\ & = \int _ { -\infty } ^ { \infty } h ( \alpha ) X ( t - \alpha) \; d \alpha \end {align*}$$

فیلم آموزش کنترل دیجیتال – مرور و حل مساله در فرادرس

کلیک کنید

در این‌جا هدف ما آن است که اثبات کنیم دو سینگال $$X ( t )$$ و $$Y ( t )$$ فرآیند‌هایی تصادفی هستند. در ابتدا می‌توان گفت مقدار میانگین $$Y ( t )$$ یا $$\mu _ Y ( t )$$، مطابق با رابطه زیر بدست می‌‌آید.

$$\begin{align*} \mu _ Y ( t ) = E [Y ( t ) ] & =E \left [ \int _ { - \infty } ^ { \infty } h ( \alpha ) X ( t - \alpha ) \; d \alpha\right] \\ & = \int _ { - \infty } ^ { \infty } h ( \alpha ) E [ X ( t - \alpha ) ] \; d \alpha \\ &=\int_{-\infty}^{\infty} h ( \alpha ) \mu _ X \; d \alpha \\ &=\mu_X \int _ { - \infty } ^ { \infty } h ( \alpha ) \; d \alpha. \end {align*}$$

همان‌طور که مشاهده می‌کنید $$\mu _ Y ( t )$$ تابعی از $$t$$ نیست. در حقیقت می‌توان $$\mu _ Y ( t )$$ را به‌صورت زیر بیان کرد:

$$\begin {align*} \mu _ Y ( t ) = \mu _ Y = \mu _ X \int _ { -\infty } ^ { \infty } h ( \alpha ) \; d\alpha \end {align*}$$

در گام بعدی تابع همبستگی متقابل یا $$R _ { X Y } ( t _ 1 , t _ 2 )$$ را می‌یابیم. این تابع برابر است با:

$$\begin{align*} R _ { X Y } ( t _ 1 , t _ 2 ) = E [X ( t _ 1 ) Y ( t _2 ) ] & = E \left [ X ( t _ 1 ) \int _ { - \infty } ^ { \infty } h ( \alpha ) X ( t _ 2 - \alpha ) \; d \alpha \right] \\ & = E \left [ \int _ { - \infty } ^ { \infty } h ( \alpha ) X ( t _ 1) X ( t_ 2 - \alpha ) \; d \alpha \right ] \\ & = \int _ { - \infty } ^ { \infty } h ( \alpha ) E [ X ( t _ 1 ) X ( t _ 2 - \alpha ) ] \; d \alpha \\ & = \int _ { - \infty } ^ { \infty } h ( \alpha ) R _ X ( t _ 1 , t _ 2 -\alpha ) \; d\alpha \\ & = \int _ { - \infty } ^{ \infty } h ( \alpha ) R _ X ( t _ 1 -t _ 2 + \ alpha ) \; d \alpha & \end{align*}$$

$$R _ { X Y } ( t _ 1 , t _ 2 )$$ تنها تابعی از $$\tau = t _ 1 - t _ 2$$ است. در نتیجه تابع همبستگی را می‌توان به‌صورت زیر بیان کرد:

$$\begin{align*} R _ { X Y } ( \tau ) & = \int _ { - \infty } ^ { \infty } h ( \alpha ) R _‌ X ( \tau + \alpha ) \; d \alpha \\ & = h ( \tau ) \ast R _ X ( - \tau ) = h ( - \tau ) \ast R _ X ( \tau) \end {align*}$$

به‌طور مشابه می‌توان گفت:

$$\begin {align*} R _ { Y } ( \tau ) = h ( \tau ) \ast h ( - \tau ) \ast R _ X ( \tau ) \end {align*}$$

با توجه به رابطه فوق می‌توان گفت که دو سیگنال $$X ( t )$$ و $$y ( t )$$ فرآیند پایا هستند.

قضیه

فرض کنید $$X ( t )$$ یک فرآیند پایا بوده و $$Y ( t )$$ نیز مطابق با رابطه زیر بدست آید.

$$\begin{align*} Y ( t ) & = h ( t ) \ast X ( t ) \end {align*}$$

در رابطه فوق $$h ( t )$$ پاسخ سیستم است. در این صورت $$X ( t )$$ و $$Y ( t )$$، فرآیند‌هایی پایا محسوب شده و سه رابطه زیر برقرار هستند.

1. $$\mu _ Y ( t ) = \mu _ Y = \mu _ X \int _ { - \infty } ^ { \infty } h ( \alpha) \; d \alpha$$
2. $$R _ { X Y } ( \tau ) = h ( - \tau ) \ast R _ X ( \tau ) = \int _ { -\infty } ^ { \infty }‌ h ( - \alpha ) R _ X ( t - \alpha ) \; d \alpha$$
3. $$R _ { Y } ( \tau ) = h ( \tau ) \ast h ( - \tau ) \ast R _ X ( \tau )$$

تحلیل دامنه فرکانس

حال می‌خواهیم قضیه ارائه شده در بالا را در دامنه فرکانس بیان کنیم. بدین منظور فرض کنید $$H ( f )$$ برابر با تبدیل فوریه تابع $$h ( t )$$ باشد. در این صورت می‌توان گفت:

$$\begin {align*} H ( f ) = \mathcal { F } \{ h ( t ) \} = \int _ { -\infty } ^ { \infty } h ( t ) e ^ { - 2‌ j \pi f t } \; dt. \end {align*}$$

$$H ( f )$$ تحت عنوان تابع انتقال سیستم شناخته می‌شود. بنابراین $$μ _ Y$$ را می‌توان به‌صورت زیر بازنویسی کرد.

$$\begin {align*} \mu _ Y = \mu _ X \int _ { - \infty } ^ { \infty } h ( \alpha) \; d \alpha \end{align*}$$

نهایتا می‌توان گفت:

$$\begin {align*} \mu _ Y = \mu _ X H ( 0 ) \end {align*}$$

از آنجایی که $$h ( t )$$ به‌عنوان یک سیگنال حقیقی در نظر گرفته شده، بنابراین داریم:

\begin{align*} \mathcal { F } \{ h ( - t ) \} = H ( - f ) = H ^ {*}(f)
\end{align*}

در رابطه فوق $$*$$ نشان‌دهنده مزدوج مختلط است. با محاسبه تبدیل فوریه از طرفین $$R _ { X Y } ( \tau ) = R _ X ( \tau ) \ast h ( - \tau )$$، رابطه زیر را می‌توان نتیجه گرفت.

\begin{align*}
S_{XY}(f)=S_X(f)H(-f)=S_X(f)H^{*}(f).
\end{align*}

نهایتا با محاسبه تبدیل فوریه از طرفین رابطه $$R _ { Y } ( \tau ) = h ( \tau ) \ast h ( - \tau ) \ast R _ X ( \tau )$$، عبارت زیر بدست می‌آید.

$$\begin{align*} S _ { Y } ( f ) & = S _ X ( f ) H ^ { * } ( f ) H ( f ) \\ & = S _ X ( f ) | H ( f ) | ^ 2 \end{align*}$$

$$\begin{align*} S _ { Y } ( f ) = S _ X ( f ) | H ( f ) | ^ 2 \end{align*}$$

مثال

فرض کنید $$X ( t )$$ فرآیندی پایا با مقدار متوسط صفر با $$R _ X ( \tau ) = e ^ { - |\tau| }$$ باشد. $$X ( t )$$ ورودی یک سیستم خطی پایای تغییرناپذیر با $$| H ( f ) |$$ زیر است.

$$\begin{align*} | H ( f ) | = \left \{ \begin {array} { l l } \sqrt { \left ( { 1 + 4 \pi ^ 2 f ^ 2 } \right) } & \quad |f| \lt 2 \\ & \quad \\ 0 & \quad | f | ≥ 2 \end {array} \right. \end {align*}$$

با فرض این‌که $$Y ( t )$$ برابر با خروجی باشد، موارد زیر را بدست آورید.

1. $$\mu _ Y ( t ) = E [ Y ( t ) ]$$
2. $$R _ Y ( \tau )$$
3. $$E [ Y ( t ) ^ 2 ]$$

توجه داشته باشید که با توجه به پایا بودن $$X ( t )$$ هر دو سیگنال $$X ( t )$$ و $$Y ( t )$$ پایا هستند.

به‌منظور یافتن $$\mu _ Y ( t )$$، می‌توان رابطه زیر را بیان کرد:

$$\begin{align*} \mu _ Y & = \mu _ X H ( 0 ) \\ & = 0 \cdot 1 = 0 \end {align*}$$

برای یافتن $$R _ Y ( \tau )$$ باید در ابتدا $$S _ Y ( f )$$ را یافت. این مقدار برابر است با:

$$\begin{align*} S _ { Y } ( f ) & = S _ X ( f ) | H( f ) | ^ 2 \end {align*}$$

تبدیل لاپلاس $$R _ X ( \tau ) = e ^ { - | \tau | }$$ نیز برابر است با:

$$\begin{align*} S _ X ( f ) & = \mathcal { F } \{ e ^ { - | \tau | } \} \\ & = \frac { 2 } { 1 + ( 2 \pi f ) ^ 2 } \end {align*}$$

بنابراین $$S _ Y ( f )$$ را می‌توان به‌صورت زیر بدست آورد.

$$\begin{align*} S _ { Y } ( f ) & = S _ X ( f ) | H ( f ) | ^‌ 2 \\ & = \left\{ \begin {array} { l l } 2 & \quad |f| \lt 2 \\ & \quad \\ 0 & \quad |f| ≥ 2 \end{array} \right. \end {align*}$$

حال می‌توان $$R _ Y ( \tau )$$ را با محاسبه لاپلاس معکوس $$S _ Y ( f )$$ بدست آورد. این عبارت برابر است با:

$$\begin{align*} R _ Y ( \tau ) = 8‌ \textrm {sinc} ( 4 \tau) \end {align*}$$

مقدار $$\sin c ( f )$$ برابر است با:

$$\begin {align*} \textrm {sinc} ( f ) = \frac { \sin ( \pi f ) } { \pi f } \end {align*}$$

نهایتا $$E [ Y ( t ) ^ 2 ]$$ نیز برابر با مقدار زیر بدست می‌آید.

$$\begin{align*} E [ Y ( t ) ^ 2 ] = R _ Y ( 0 ) = 8 . \end {align*}$$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی و آمار آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• توزیع‌های آماری — مجموعه مقالات جامع وبلاگ فرادرس
• واریانس و انحراف معیار — به زبان ساده
• اثر ماتریس (Trace) در جبر خطی — به زبان ساده

^^