مدارهای مغناطیسی – به زبان ساده

اثرات مغناطیسی و الکترومغناطیسی، نقش مهمی در طراحی طیف گسترده‌ای از سیستم‌های الکتریکی و الکترونیکی ایفا می‌کنند. الکترومغناطیس در موتورها، ژنراتورها، ترانسفورماتورها، بلندگوها، رله‌ها، تجهیزات پزشکی و... کاربرد اساسی دارد. پاسخ و مشخصه بخش مغناطیسی و الکترومغناسی این سیستم‌ها، بر سطوح جریان و ولتاژ سیستم، بازده طراحی، اندازه سیستم و هر ویژگی مهم دیگر تاثیرگذار است.

خوشبختانه، شباهت زیادی در تحلیل مدارهای الکتریکی و مدارهای مغناطیسی وجود دارد و به همین دلیل با استفاده از قوانین حاکم بر مدارهای الکتریکی، می‌توان مدارهای مغناطیسی را به‌آسانی تحلیل کرد. در این آموزش، ابتدا کمیت‌های موجود در مدارهای مغناطیسی را معرفی کرده، سپس روابط حاکم بر آن‌ها را بیان و در نهایت، چند مثال را ارائه خواهیم کرد.

خطوط مغناطیسی گذرنده از یک سطح را «شار» (flux) یا فلو مغناطیسی می‌گویند و آن را با $$\phi$$ نشان می‌دهند. واحد شار، وِبِر (Wb) است. شار مغناطیسی در الکترومغناطیس شبیه جریان در مدار الکتریکی است و خطوط آن، کوتاه‌ترین مسیر را با بالاترین «نفوذپذیری» یا ضریب نفوذ (Permeability) برای حرکت انتخاب می‌کنند.

«چگالی شار» (Flux density) به‌صورت زیر تعریف می‌شود:

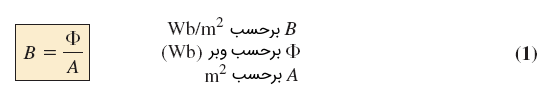
نیروی عامل تولید شار در مدارهای مغناطیسی، «نیروی محرک مغناطیسی» (Magnetomotive force) یا mmf نامیده می‌شود و واحد آن، آمپر-دور (A.T) است. نیروی محرک مغناطیسی، مستقیماً به تعداد دورها و جریان هسته مغناطیس‌کننده از طریق رابطه زیر مرتبط است:

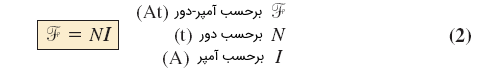
اندازه شار مغناطیسی در هسته فرومغناطیسی تابعی از نفوذپذیری مواد است. مواد «فِرومغناطیس» (Ferromagnetic)، سطح بالایی از نفوذپذیری دارند، در حالی که مواد غیرمغناطیسی مانند هوا و چوب، نفوذپذیری بسیار کمی دارند. میزان نفوذپذیری ماده نسبت به هوا، نفوذپذیری نسبی نامیده شده و با رابطه زیر تعریف می‌شود:

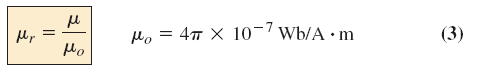
مقادیر $$\mu _r$$ را نمی‌توان در یک جدول نشان داد، زیرا مقدار آن، با سایر کمیت‌های مدار مغناطیسی تعیین می‌شود. با تغییر نیروی محرک مغناطیسی، نفوذپذیری نیز تغییر می‌کند.

«رلوکتانس» (Reluctance) یا مقاومت مغناطیسی، پارامتری شبیه مقاومت در مدارهای الکتریکی است و مقدار آن برای یک ماده با رابطه زیر تعریف می‌شود:

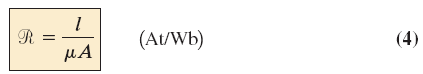
در رابطه بالا، R رلوکتانس، l طول مسیر مغناطیسی و A مساحت مقطعی است که شار از آن می‌گذرد.

همان‌طور که می‌دانیم، قانون اهم در مدارهای الکتریکی بر اساس این واقعیت است اختلاف پتانسیل دو سر یک مقاومت سبب ایجاد جریان می‌شود. به‌صورت عمومی‌تر می‌توان نوشت:

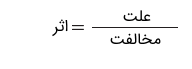
در مدارهای مغناطیسی، اثر مطلوب، شار $$\Phi$$ است. همچنین علت، نیروی محرکه مغناطیسی (mmf) است که نیروی خارجی مورد نیاز را برای ایجاد خطوط شار مغناطیسی در ماده مغناطیسی تامین می‌کند. مخالفت برقراری شار $$\Phi$$ نیز همان رلوکتانس R است.

با گنجاندن مطالب مذکور در یک رابطه ریاضی، داریم:

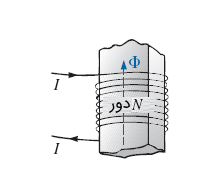
از آن‌جایی که $$F=NI$$، رابطه (5) بیان می‌کند که با افزایش تعداد دور یا جریان گذرنده از سیم‌پیچ، در شکل زیر، می‌توان خطوط شار هسته را بیش‌تر کرد.

نیروی الکترومغناطیسی در واحد طول (چگالی شار)، «نیروی مغناطیس‌کنندگی» (Magnetizing force) نامیده می‌شود که معادله آن به‌صورت زیر است:

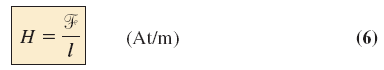
با جایگذاری رابطه نیروی الکترومغناطیسی در فرمول بالا، داریم:

جهت شار را می‌توان با استفاده از قانون دست راست تعیین کرد؛ بدین صورت که چهار انگشت را در جهت گردش جریان قرار داده و انگشت شست، جهت شار را تعیین می‌کند. لازم به ذکر است که نیروی مغناطیس‌کنندگی، مستقل از نوع ماده هسته است و تنها با تعداد دور سیم‌پیچ، جریان آن و طول هسته تعیین می‌شود.

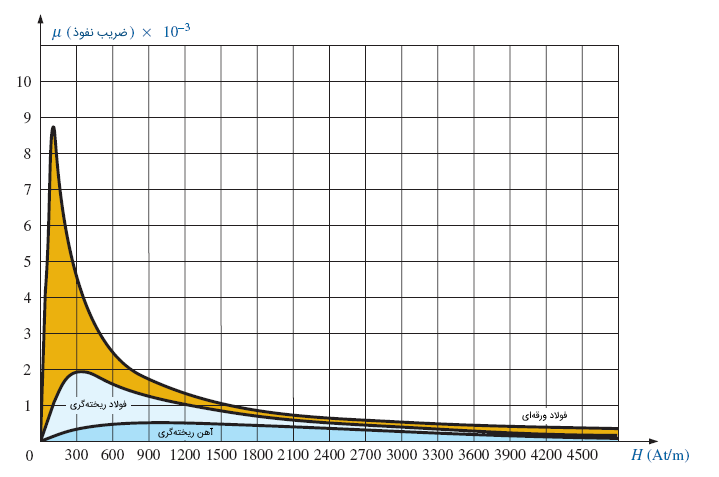
نیروی مغناطیس‌کنندگی اعمالی یک اثر واضح روی نفوذپذیری ماده مغناطیسی دارد. مطابق شکل زیر، وقتی نیروی مغناطیس‌کنندگی افزایش یابد، نفوذپذیری نیز زیاد شده و به یک مقدار حداکثر می‌رسد، سپس افت می‌کند و به مقدار حداقل می‌رسد.

چگالی شار و نیروی مغناطیس‌کنندگی را می‌توان با رابطه زیر به هم ربط داد:

منحنی B-H یک ماده فرومغناطیس مانند فولاد، شبیه شکل زیر است:

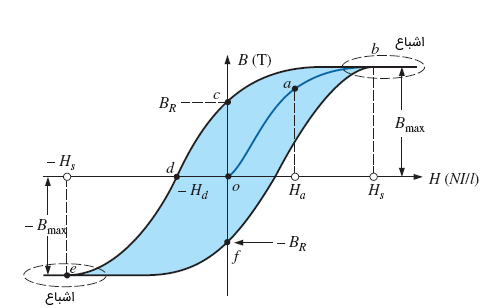
به منحنی بالا، منحنی هیسترزیس (Hysteresis) می‌گویند. طبق این شکل، چنانچه یک جریان با دامنه بزرگ به هسته اعمال شده، سپس این جریان برداشته شود، منحنی، مسیر abc را طی می‌کند، وقتی نیروی محرکه از هسته برداشته شود شار هسته صفر نمی‌شود بلکه مقداری میدان مغناطیسی در هسته باقی می‌ماند که به آن، میدان مغناطیسی هیسترزیس یا پسماند می‌گویند.

اگر چرخه شکل بالا کامل شود، سایر منحنی‌ها را می‌توان با داشتن حداکثر مقدار نیروی مغناطیس‌کنندگی H به‌دست آورد:

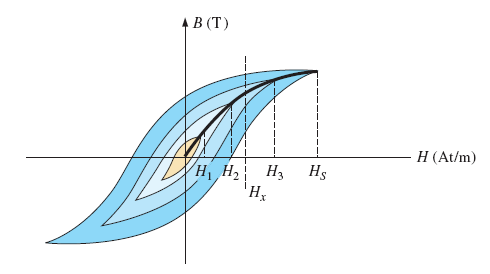
برای مقدار مشخصی از H که آن را $$H_x$$ می‌نامیم، مقادیر مختلفی از B وجود دارد. برای تعیین مقدار B از روی H، می‌توانیم انتهای حلقه‌های هیسترزیس را به هم وصل کنیم. با اتصال این نقطه‌ها، یک منحنی به‌دست می‌آید که در شکل بالا با خط پررنگ نشان داده شده است و منحنی مغناطیس‌شوندگی نامیده می‌شود.

منحنی مغناطیس‌شوندگی چند ماده مختلف در شکل زیر نشان داده شده است.

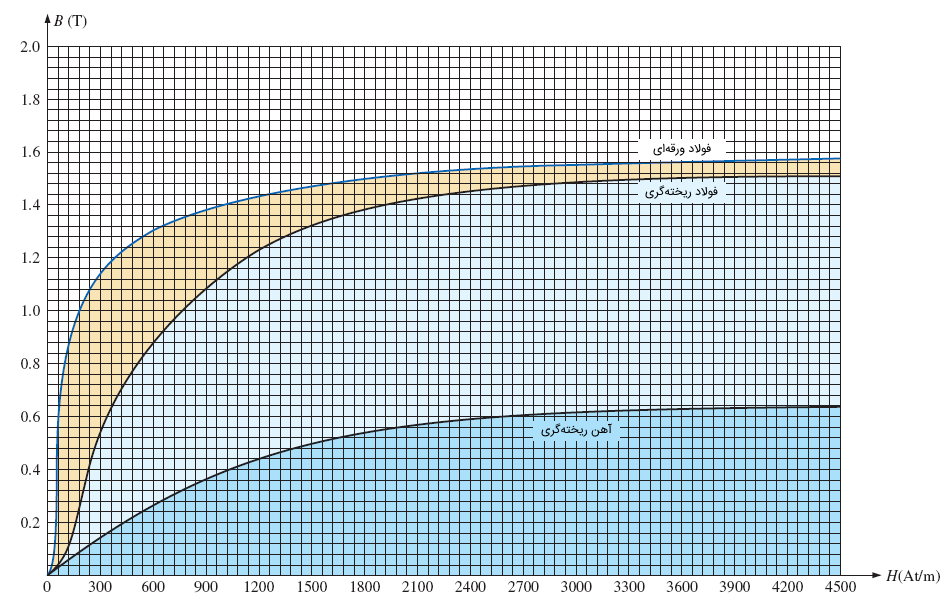
حال می‌خواهیم، مدارهای مغناطیسی را مشابه مدارهای الکتریکی تحلیل کنیم. مشابه قانون ولتاژ‌ کیرشهف، برای یک مدار مغناطیسی داریم:

به عبارت دیگر، مجموع جبری mmf در یک حلقه بسته از مدار مغناطیسی برابر با صفر است. معادلات زیر در مدارهای مغناطیسی برقرار است:

برای مثال، مدار مغناطیسی شکل زیر را ببینید که از چند ماده فِرومغناطیس تشکیل شده است.

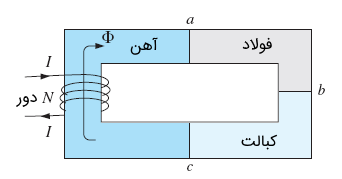
با استفاده از قانون ولتاژ کیرشهف، داریم:

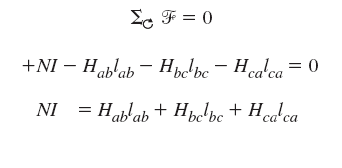
همه عبارات معادله بالا معلوم هستند، جز نیروی مغناطیس‌کنندگی که برای هر بخش از مدار مغناطیسی، می‌توان آن را با داشتن چگالی شار B از منحنی B-H به‌دست آورد.

توزیع شار در مدار مغناطیسی بالا، به‌شکل زیر است:

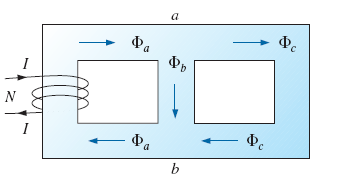
معادلات تقسیم شار مربوط به آن را نیز می‌توان به‌صورت زیر نوشت:

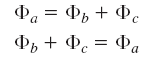
در مدار مغناطیسی، گاهی «فاصله هوایی» (Air gaps) نیز وجود دارد. شکل زیر فاصله هوایی را در دو حالت ایده‌آل (شکل سمت راست) و دارای خمیدگی شار (شکل سمت چپ) نشان می‌دهد.

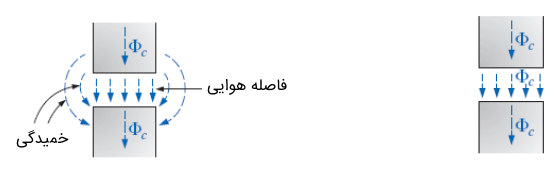
روابط حاکم بر فاصله هوایی، به‌صورت زیر است:

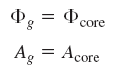
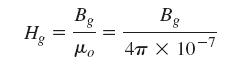
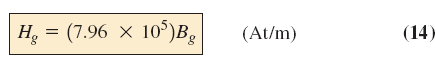
در ادامه، چند مثال را بررسی می‌کنیم.

مثال ۱

مدار مغناطیسی سری شکل زیر را در نظر بگیرید.

مقدار جریان $$I$$ مورد نیاز را برای برقراری شار مغناطیسی $$4 \times 10^{-4}$$ وبر بیابید. همچنین مقدار $$\mu$$ و $$\mu _r$$ را محاسبه کنید.

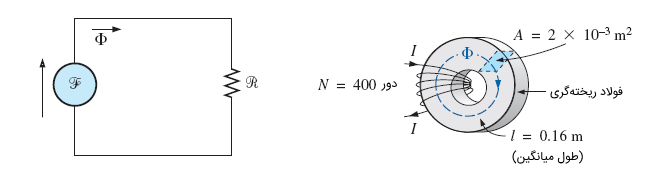
حل: چگالی شار $$B$$ را می‌توان با رابطه زیر محاسبه کرد:

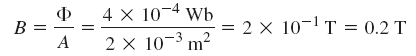
با استفاده از منحنی B-H می‌توانیم نیروی مغناطیس‌کنندگی H را تعیین کنیم:

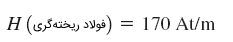
اگر قانون مداری آمپر را به‌کار ببریم، جریان به‌صورت زیر به‌دست می‌آید:

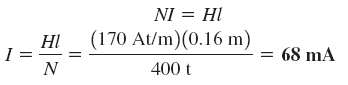
ضرایب نفوذ مغناطیسی نیز به‌شکل زیر محاسبه می‌شوند:

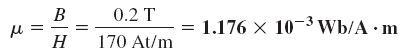
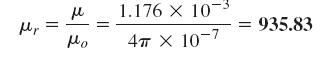
مثال ۲

مدار مغناطیسی شکل زیر، از دو بخش آهن ریخته‌گری و فولاد ورقه‌ای تشکیل شده است. جریان مورد نیاز $$I$$ را برای برقراری شار نشان داده شده در شکل پیدا کنید.

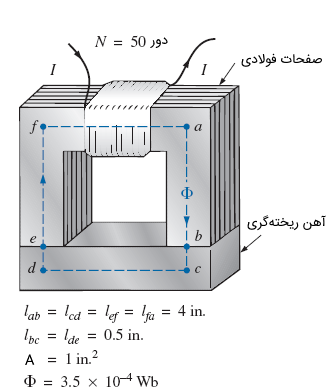
حل: ابتدا طول و سطح مقطع را برای دو بخش و برحسب یکاهای SI به‌دست می‌آوریم. محاسبه این پارامترها و تبدیل مربوط به آن‌ها به‌صورت زیر است (1 اینچ برابر با 2.54 سانتی‌متر است).

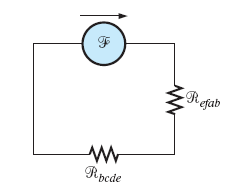
مدار معادل شکل بالا به‌صورت زیر نشان داده می‌شود:

چگالی شار هر بخش را نیز می‌توان با فرمول زیر محاسبه کرد:

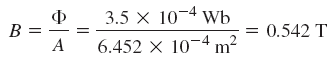
نیروی مغناطیس‌کنندگی برای فولاد ورقه‌ای و آهن ریخته‌گری، به‌ترتیب برابر با 70 و 1600 آمپر-دور بر متر است.

اکنون می‌توانیم $$Hl$$ را برای هر بخش تعیین کنیم:

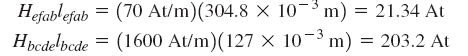
همچنین با استفاده از تساوی $$NI=Hl$$ داریم:

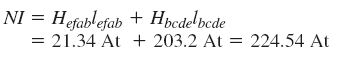
اکنون، با توجه به معادله بالا، مقدار جریان به‌دست می‌آید:

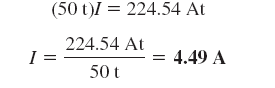
مثال ۳

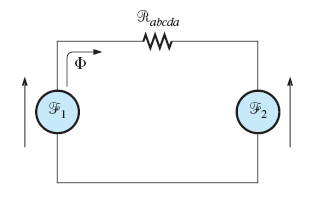
جریان ثانویه $$I_2$$ ترانسفورماتور شکل زیر را برای حالتی به‌دست آورید که شار $$1.5 \times 10^{-5}$$ در جهت عقربه‌های ساعت از آن بگذرد.

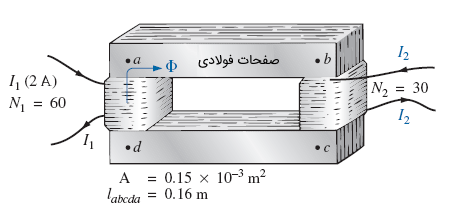
حل: مدار معادل شکل بالا به‌صورت زیر است:

چگالی شار با رابطه زیر محاسبه می‌شود:

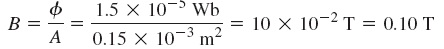
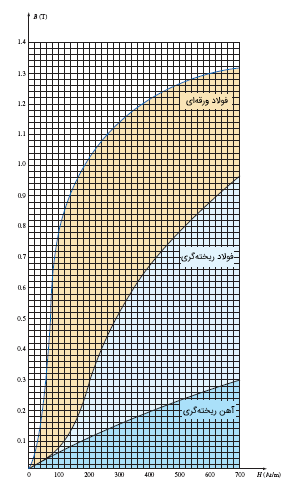
با داشتن مقدار B، می‌توانیم مقدار H را از منحنی زیر پیدا کنیم.

بنابراین، مقدار نیروی مغناطیس‌کنندگی، برابر است با

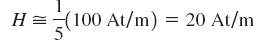
با داشتن مقدار H، می‌توان جریان را با نوشتن معادلات زیر حساب کرد:

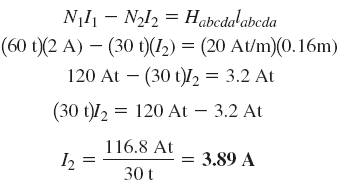
مثال ۴

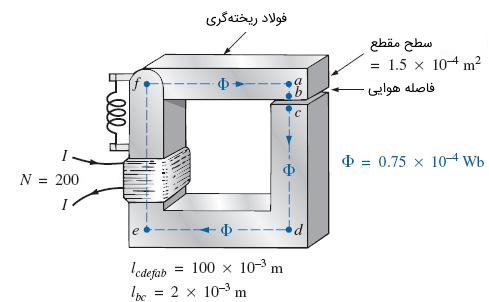
در مدار مغناطیسی شکل زیر، مقدار $$I$$ را به‌گونه‌ای محاسبه کنید که شار $$\Phi = 0.75 \times 10^{-4}$$ وبر برقرار شود.

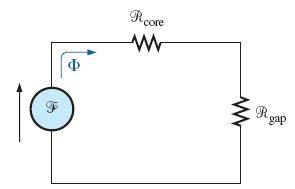
حل: مدار معادل شکل بالا، به‌صورت زیر است:

ابتدا، چگالی شار را محاسبه می‌کنیم:

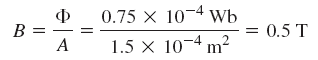
از نمودار منحنی مغناطیس‌شوندگی که در مثال 3 نشان داده شد، مقدار نیروی مغناطیس‌کنندگی تقریباً 280 آمپر-دور بر متر به‌دست می‌آید. برای فاصله هوایی نیز داریم:

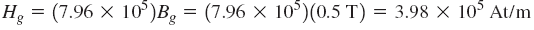
با داشتن نیروی مغناطیس‌کنندگی و طول هر یک از قسمت‌های مدار، می‌توانیم مقدار نیروی محرکه مغناطیسی را محاسبه کنیم:

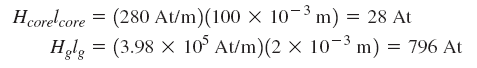
در گام آخر، با اعمال قانون مداری آمپر، جریان را تعیین می‌کنیم:

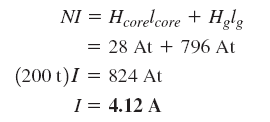
همان‌طور که از محاسبات بالا مشخص است، فاصله هوایی، آمپر-دور بسیار بیشتری نسبت به سایر بخش‌های مدار نیاز دارد. دلیل این امر، غیرمغناطیسی بودن هوا است.

مثال ۵

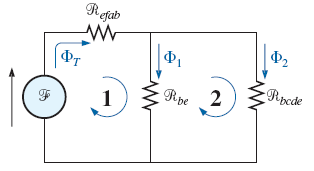
جریان مورد نیاز $$I$$‌ را برای برقراری شار $$\Phi = 1.5 \times 10^{-4}$$ وبر برای ساق نشان داده شده در شکل زیر پیدا کنید.

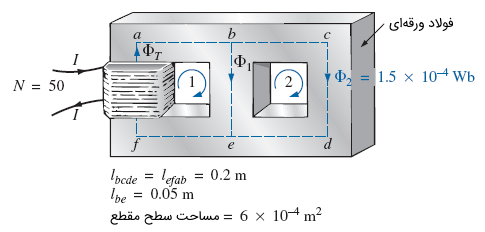
حل: شکل زیر، مدار معادل مدار مغناطیسی را نشان می‌دهد.

با داشتن مقدار $$\Phi _2$$، مقدار $$B_2$$‌ را محاسبه می‌کنیم:

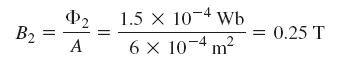
با منحنی B-H مثال ۳، مقدار تقریبی نیروی مغناطیس‌کنندگی نیز به‌دست می‌آید:

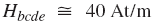
حال، از قانون مداری آمپر در حلقه 2  استفاده می‌کنیم:

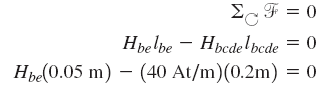
پاسخ معادله بالا، نیروی مغناطیس‌کنندگی زیر است:

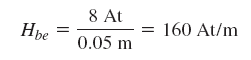
بار دیگر از منحنی B-H‌ کمک می‌گیریم و این بار، مقدار چگالی شار را از روی آن تعیین می‌کنیم:

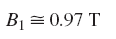
از روی چگالی شار، مقدار شار به‌آسانی به‌دست می‌آید:

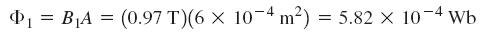
اکنون می‌توانیم شار کلی را محاسبه و با کمک آن و منحنی B-H، مقدار نیرو را نیز تعیین کنیم:

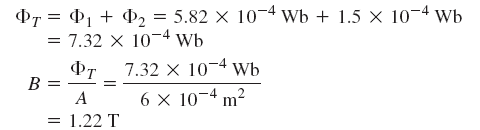
در نهایت، با استفاده از قانون مداری آمپر، جریان به‌دست می‌آید:

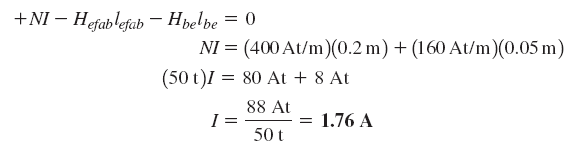
مثال ۶

شار مغناطیسی $$\Phi$$‌ را در مدار شکل زیر بیابید.

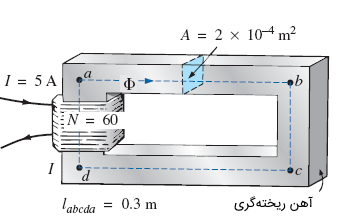
حل: ابتدا، نیروی مغناطیس‌‌کنندگی را محاسبه می‌کنیم:

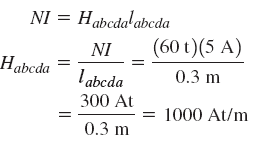
با استفاده از منحنی B-H، مقدار چگالی شار تقریباً باربر با 0.39 تسلا به‌دست می‌آید. در نتیجه، می‌توانیم مقدار شار مغناطیسی را با فرمول زیر محاسبه کنیم:

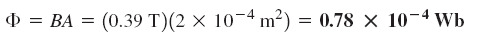
اگر به یادگیری مباحث مشابه این مطلب علاقه‌مند هستید، پیشنهاد می‌کنیم آموزش‌های زیر را نیز مشاهده کنید:

• مجموعه آموزش‌های مهندسی قدرت
• مجموعه آموزش‌های مهندسی برق
• مجموعه آموزش‌های دروس مهندسی برق
• آموزش ماشین های الکتریکی 1
• آموزش مبانی مهندسی برق 2
• آموزش ماشین های الکتریکی 1 (مرور و حل تست کنکور ارشد)
• کنترل سرعت موتورهای DC — از صفر تا صد

^^