پیاده سازی روش نیوتون رافسون در پایتون — راهنمای کاربردی

پیدا کردن ریشههای توابع و معادلات برای شناخت و تحلیل آنها حائز اهمیت است. از طرفی، تنها برای تعداد بسیار محدودی از توابع، روش حل بسته ریاضیاتی وجود دارد. به همین دلیل، روشهای عددی برای حل معادلات اهمیت پیدا میکنند. یکی از پرکاربردیترین روشهای عددی برای ریشهیابی توابع، «روش نیوتون رافسون» (Newton Raphson Method) به حساب میآید که در این روش، برای پیدا کردن ریشه از مقدار تابع و مشتق آن استفاده میشود. در این مقاله به پیاده سازی روش نیوتون رافسون در پایتون پرداخته شده است.
روش نیوتون رافسون چیست ؟
روش نیوتون رافسون بیان میکند که اگر قصد ریشهیابی تابع $$ f_{(x)} $$ با تخمین اولیه $$ x_0 $$ وجود داشته باشد، میتوان با تکرارهای کافی با دقت خوبی به صورت زیر مقدار ریشه را پیدا کرد:
$$ x_{n+1} = x_n - \frac{f_{(x_n)}}{f'_{(x_n)}} $$
به این ترتیب، با داشتن یک تخمین اولیه، میتوان به $$ x_1, x_2, \dots $$ دست یافت که به طور کلی با افزایش دقت نیز افزایش پیدا میکند.
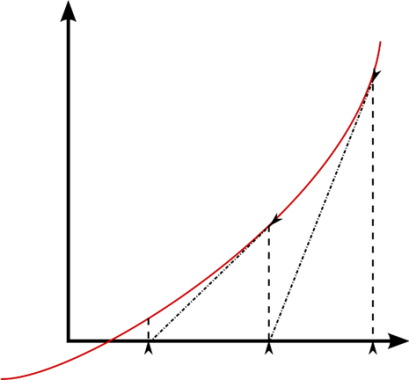
نکته دیگری که باید به آن توجه شود، استفاده از مشتق تابع در مخرج کسر است. از آن جایی که هدف یافتن یک روش عمومی برای ریشهیابی تمامی توابع است، باید مشتق تابع را نیز به صورت عددی محاسبه کرد. برای مشتق عددی هر تابع پیوسته در محل مشتقگیری نیز میتوان به صورت زیر نوشت:
$$ f'_{(x)} = \frac{f_{(x+h)} - f_{(x-h)}}{2h} $$
به این ترتیب، میتوان رابطه را تنها براساس $$ f_{(x)} $$ بازنویسی کرد. اکنون در ادامه به پیاده سازی روش نیوتون رافسون پرداخته شده است.
پیاده سازی روش نیوتون رافسون در پایتون
پس از ارائه مباحث نظری پیرامون روش نیوتون رافسون، در این بخش به چگونگی پیادهسازی این الگوریتم در پایتون پرداخته میشود. طبق روال معمول، اولین مرحله، فراخوانی کتابخانههای مورد نیاز برای انجام این پیادهسازی است که در ادامه به آن پرداخته شده است.
فراخوانی کتابخانههای مورد نیاز برای پیاده سازی روش نیوتون رافسون در پایتون
جهت پیاده سازی روش نیوتون رافسون در پایتون به کتابخانههایی برای محاسبات ریاضیاتی، کار با آرایهها و رسم نمودار نیاز است. بنابراین، وارد محیط برنامهنویسی شده و باید کتابخانههای مورد نیاز به صورت زیر فراخوانی شوند:
1import math as mt
2import numpy as np
3import matplotlib.pyplot as pltتعریف تابع ریشه یاب برای پیاده سازی روش نیوتون رافسون در پایتون
اکنون باید تابع ریشهیاب تعریف شود. این تابع، تخمین اولیه، تعداد مراحل تکرار و مقدار h را در ورودی دریافت میکند. تعریف یا همان اعلان این تابع به صورت زیر است:
1def NewtonRaphson(Function, x0:float, N:int=20, h:float=1e-4):باید توجه داشت که چون مقدارهای N و h به طور تجربی میتوانند تعیین شوند و وابستگی کمی به شرایط تابع دارند، بهتر است برای آنها مقدار پیشفرض تعریف شود. حال میتوان حلقه اصلی تابع را تعریف کرد که به تعداد N بار تکرار میشود:
1def NewtonRaphson(Function, x0:float, N:int=20, h:float=1e-4):
2 for n in range(N):برای اینکه آخرین تخمین تابع از ریشه نیز ذخیره شود، باید متغیری به نام $$ x $$ تعریف کرد که در ابتدای تابع، برابر با $$ x_0 $$ است:
1def NewtonRaphson(Function, x0:float, N:int=20, h:float=1e-4):
2 x = x0
3 for n in range(N):حال میتوان رابطه (فرمول) مربوطه را داخل تابع پیادهسازی کرد:
1def NewtonRaphson(Function, x0:float, N:int=20, h:float=1e-4):
2 x = x0
3 for n in range(N):
4 x = x - Function(x) / Derivative(Function, x, h)همانطور که ملاحظه میشود، در خط کد فوق رابطه مربوطه پیادهسازی شده است. حال در ادامه به پیادهسازی تابع مشتق عددی پرداخته میشود.
تعریف تابع مشتق عددی برای پیاده سازی تابع ریشه یاب
باید توجه داشت که برای پیادهسازی تابع مشتق عددی، باید به شکل زیر عمل کرد:
1def Derivative(Function, x:float, h:float):
2 d = (Function(x + h) - Function(x - h)) / (2*h)
3 return dاین تابع در ورودی تابع مورد نظر، محل مشتقگیری و گام حرکتی را دریافت میکند و در خروجی مقدار عددی مشتق را بازمیگرداند.
نمایش مقدار تابع در هر مرحله برای تعریف تابع ریشه یاب
حال میتوان داخل تابع اصلی با استفاده از دستور print مقدار تابع در هر مرحله را نشان داد:
1def NewtonRaphson(Function, x0:float, N:int=20, h:float=1e-4):
2 x = x0
3 print(f'Iteration {0}: {x = } -- y = {Function(x)}')
4 for n in range(N):
5 x = x - Function(x) / Derivative(Function, x, h)
6 print(f'Iteration {n+1}: {x = } -- y = {Function(x)}')در نهایت باید مقدار ریشه بازگردانده شود:
1def NewtonRaphson(Function, x0:float, N:int=20, h:float=1e-4):
2 x = x0
3 print(f'Iteration {0}: {x = } -- y = {Function(x)}')
4 for n in range(N):
5 x = x - Function(x) / Derivative(Function, x, h)
6 print(f'Iteration {n+1}: {x = } -- y = {Function(x)}')
7 return xآزمایش تابع ریشه یابی ایجاد شده با استفاده از یک مثال
حال اگر تابع زیر برای ریشهیابی وجود داشته باشد:
$$ f_{(x)} = 2^x - x^2 $$
برای ریشهیابی آن میتوان به صورت زیر عمل کرد:
1def Func1(x:float):
2 return 2**x - x**2
3
4x = NewtonRaphson(Func1, 1, N=8)که پس از اجرا نتایج زیر حاصل خواهند شد:
Iteration 0: x = 1 -- y = 1 Iteration 1: x = 2.629445679580636 -- y = -0.726102607396632 Iteration 2: x = 1.8807152492127912 -- y = 0.145486022977461 Iteration 3: x = 2.0010646793622606 -- y = -0.00130684350311 Iteration 4: x = 2.0000000356631285 -- y = -4.3773325408e-08 Iteration 5: x = 2.0000000000000004 -- y = -8.8817841970e-16 Iteration 6: x = 1.9999999999999998 -- y = 4.44089209850e-16 Iteration 7: x = 2.0 -- y = 0.0 Iteration 8: x = 2.0 -- y = 0.0
به این ترتیب ملاحظه میشود که $$ x =2 $$ به عنوان ریشه پیدا میشود که مقدار تابع نیز در این نقطه دقیقاً برابر با $$ 0 $$ است. حال اگر نقطه شروع به $$ x_0 = 0$$ تغییر دهیم، نتایج زیر حاصل میشود:
ITERATION 0: X = 0 -- Y = 1 ITERATION 1: X = -1.4426950397336544 -- Y = -1.7134895362060 ITERATION 2: X = -0.8970645796858707 -- Y = -0.2677466617320 ITERATION 3: X = -0.7734702256475462 -- Y = -0.0132475754264 ITERATION 4: X = -0.7666850787387707 -- Y = -3.955810434E-05 ITERATION 5: X = -0.7666646961459681 -- Y = -3.567960371E-10 ITERATION 6: X = -0.766664695962123 -- Y = 1.11022302462E-16 ITERATION 7: X = -0.7666646959621232 -- Y = -1.110223024E-16 ITERATION 8: X = -0.766664695962123 -- Y = 1.11022302462E-16
همانطور که مشاهده میشود، الگوریتم به $$ x = -0.766 $$ همگرا شده است. بنابراین، تخمین اولیه از ریشه، نقش تعیینکنندهای در نتیجه الگوریتم دارد.
نمایش نتایج روش نیوتون رافسون روی نمودار در پایتون
برای بررسی این مورد، میتوان اعداد بین $$ x_0 = -3 $$ تا $$ x_0 = +3 $$ را به الگوریتم داده و نتایج آن را روی نمودار مشاهده کرد:
1X0 = np.linspace(-3, +3, num=300)
2
3X = np.zeros(300)
4
5for i in range(300):
6 X[i] = NewtonRaphson(Func1, X0[i], N=30, h=1e-5)به این ترتیب، 300 عدد در بازه $$ [-3, +3] $$ انتخاب میشوند و داخل یک حلقه، مقدار ریشه حاصل در آرایه $$ X $$ ذخیره میشود. حال میتوان مقدار $$ X $$ را برحسب $$ X_0 $$ رسم کرد:
1plt.scatter(X0, X, s=10, c='crimson')
2plt.xlabel('x0')
3plt.ylabel('x (After 20 Iteration)')
4plt.show()در خروجی، نمودار زیر حاصل خواهد شد:
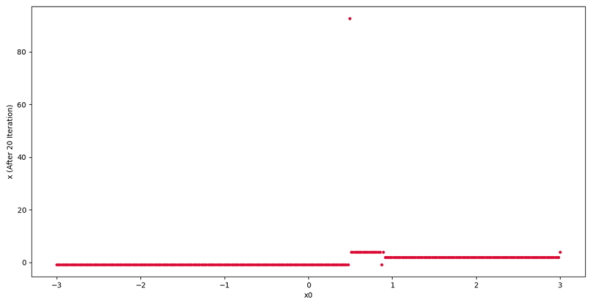
بنابراین مشاهده میشود که اغلب نقاط به سه ریشه همگرا شدهاند ولی یک نقطه نتوانسته به خوبی همگرا شود. با فیلتر کردن نمودار نتیجه به صورت زیر خواهد بود:
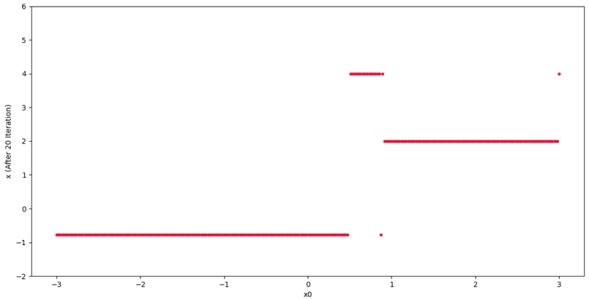
به این ترتیب مشاهده میشود که اغلب نقاط روی جواب $$ x = -0.766 $$ همگرا شدهاند. به این صورت میتوان با افزایش تعداد نقاط شروع، تعداد ریشههای بیشتری را پیدا کرد. حال اگر تابع دیگری با تعداد ریشههای بیشتر وجود داشته باشد:
$$ f_{(x)} = \frac{\sin(x^2)}{x} $$
نمودار تابع فوق به صورت زیر است:
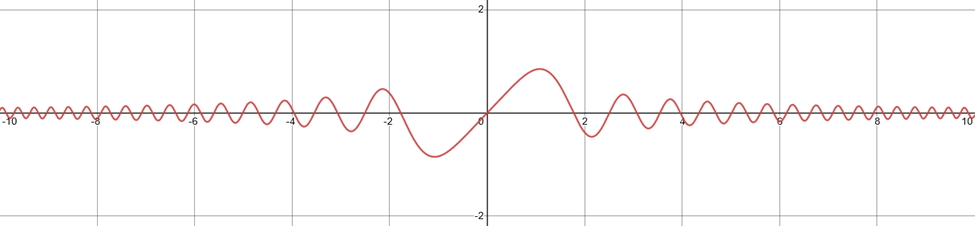
برای این تابع نمودار خروجی روش نیوتون رافسون به صورت زیر خواهد بود:
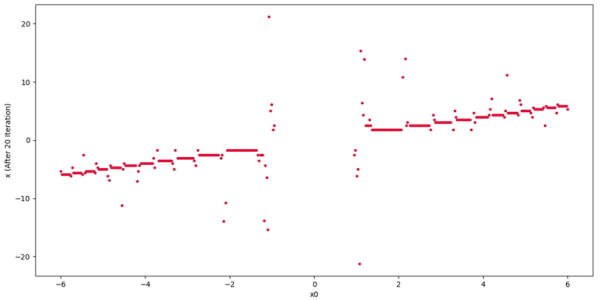
که مشاهده میشود ریشههایی از -۲۰ تا +۲۰ پیدا شدهاند. اگر قصد نمایش دادن این ریشهها روی نمودار وجود داشته باشد، به صورت زیر عمل میشود:
1def Func2(x:float):
2 return mt.sin(x**2) / x
3
4X0 = np.linspace(-6, +6, num=400)
5Y0 = np.zeros(400)
6
7X = np.zeros(400)
8Y = np.zeros(400)
9
10for i in range(400):
11 Y0[i] = Func2(X0[i])
12 X[i] = NewtonRaphson(Func2, X0[i], N=60, h=1e-5)
13 Y[i] = Func2(X[i])
14
15plt.plot(X0, Y0, ls='-', lw=1.2, c='crimson', label='Function')
16for x in X[Y<1e-3]:
17 if x<+6 and x>-6:
18 plt.plot([x, x], [-2, +2], c='teal', ls='--', lw=0.8)
19plt.xlabel('x')
20plt.ylabel('y')
21plt.axhline(c='k')
22plt.axvline(c='k')
23plt.legend()
24plt.show()باید توجه داشت که شرط قبول شدن یک عدد به عنوان ریشه این است که مقدار تابع در آن نقطه عددی بسیار نزدیک به 0 باشد که در این بخش عدد 0.001 به عنوان شرط تعیین شده است. در خروجی نمودار زیر حاصل میشود:
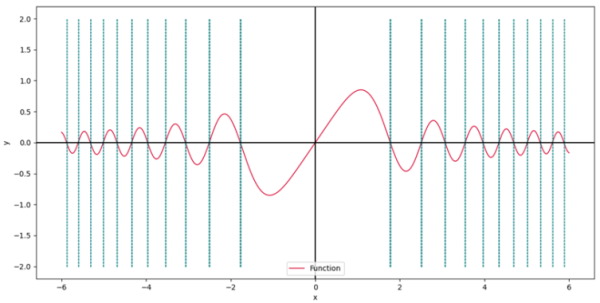
در نمودار فوق مشاهده میشود که تمامی ریشهها به درستی پیدا شدهاند.
جمعبندی
به طور کلی در این مطلب به پیادهسازی روش نیوتون رافسون پرداخته شد و نتایج آن روی نمودارها بررسی شدند. این نتایج نشاندهنده این نکته هستند که روشهای عددی میتوانند برای حل طیف وسیعی از مسائل مختلف کارآمد باشند. برای بررسیهای بیشتر میتوان اثر N و h بر روی نتایج را بررسی و سرعت همگرایی در حالتهای مختلف را با هم مقایسه کرد.










