پیاده سازی روش نیوتون رافسون | راهنمای کاربردی

در این مطلب، پیاده سازی روش نیوتون رافسون در زبان‌های برنامه‌نویسی گوناگون همراه با ارائه کدهای کامل، انجام شده است.

پیاده سازی روش نیوتون رافسون

تابع f(x)‎ روی یک نقطه ممیز شناور x و یک حدس اولیه برای ریشه آن داده شده است. هدف پیدا کردن ریشه تابع در بازه است. در اینجا، f(x)‎ نشانگر یک معادله جبری یا غیر جبری است. برای سادگی بیشتر، فرض می‌شود که مشتق تابع نیز به عنوان ورودی داده شده است.

فیلم آموزش روش های عددی ریشه یابی و حل معادلات و پیاده سازی در متلب MATLAB در فرادرس

کلیک کنید

مثال زیر به درک بهتر این مسئله کمک شایان توجهی می‌کند.

Input: A function of x (for example x3 – x2 + 2),
       derivative function of x (3x2 – 2x for above example)
       and an initial guess x0 = -20
Output: The value of root is : -1.00
        OR any other value close to root.

در ادامه، روش نیوتون رافسون با «روش دو بخشی» (Bisection Method) و «روش نابجایی» (The Method Of False Position) مقایسه شده است.

• در روش‌های دوبخشی و نابجایی، یک بازه داده می‌شد. در اینجا، تنها یک حدس اولیه از مقدار ریشه ارائه می‌شود.
• همگرا شدن در دو روش مذکور، تضمین شده است؛ اما روش نیوتون رافسون ممکن است در برخی از حالات همگرا نشود.
• روش نیوتون رافسون نیازمند مشتق است. این در حالی است که مشتق‌گیری از برخی توابع، بسیار دشوار و یا غیر ممکن است.
• در بسیاری از مسائل، روش نیوتون رافسون سریع‌تر از دو روش دیگر بیان شده، همگرا می‌شود.
• روش نیوتون رافسون می‌تواند ریشه‌های تکرار شده را تشخیص دهد، زیرا صراحتاً به دنبال تغییرات در علامت f(x)‎ نیست.

فرمول

با شروع از حدس اولیه x₁، روش نیوتون رافسون از رابطه زیر برای پیدا کردن مقدار بعدی x، یعنی x_n+1 از مقدار پیشین x_n استفاده می‌کند.

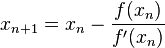
الگوریتم

ورودی: مقدار اولیه x، تابع func(x)‎، مشتق تابع derivFunc(x)‎

خروجی: ریشه تابع Func()‎

1. محاسبه مقادیر func(x)‎ و derivFunc(x)‎ برای مقدار اولیه x
2. محاسبه h: h = func(x) / derivFunc(x)‎
3. تا هنگامی که h، بزرگ‌تر از خطای پذیرفته ε است
   1. h = func(x) / derivFunc(x)‎
   2. x = x – h

در ادامه، پیاده‌سازی روش نیوتون رافسون در زبان‌های برنامه‌نویسی گوناگون انجام شده است.

پیاده سازی روش نیوتون رافسون در ++C

پیاده سازی روش نیوتون رافسون در جاوا

پیاده سازی روش نیوتون رافسون در پایتون

پیاده سازی روش نیوتون رافسون در #C

پیاده سازی روش نیوتون رافسون در PHP

خروجی قطعه کدهای بالا به صورت زیر است.

The value of root is : -1.00

روش کار برنامه‌های ارائه شده در بالا

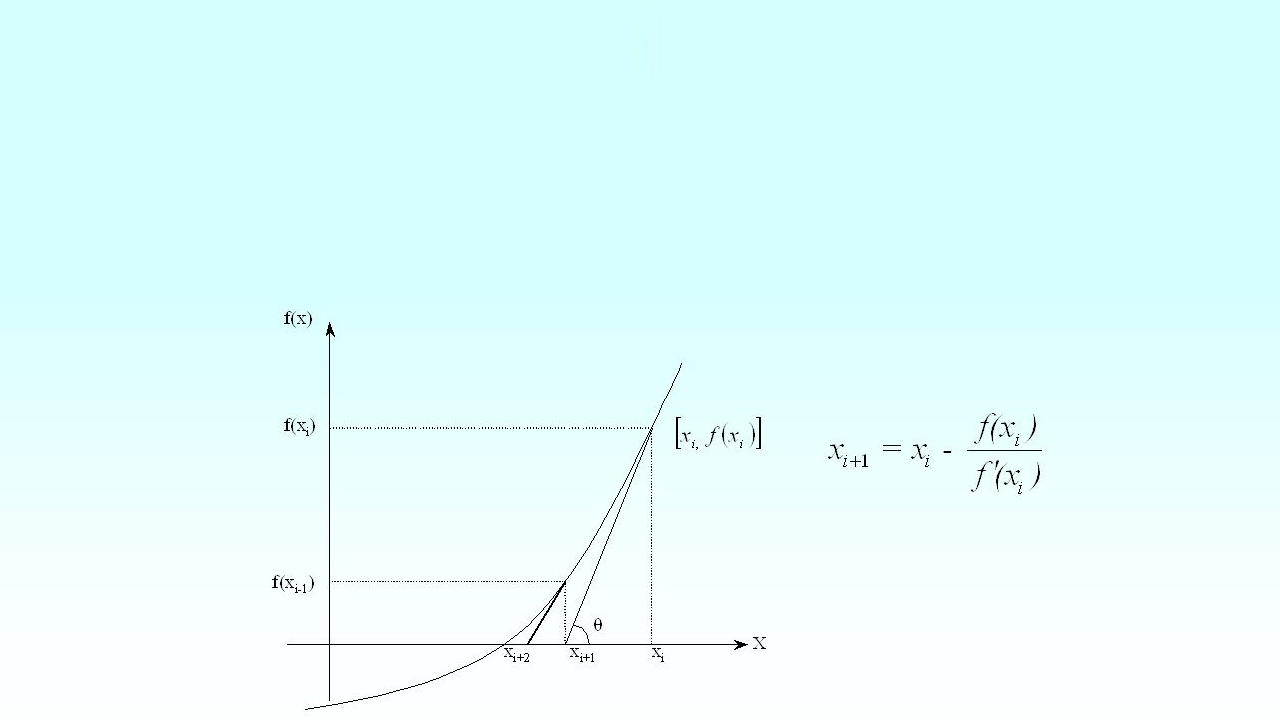
ایده کلی آن است که یک خط مماس بر f(x)‎ در نقطه x₁ ترسیم شود. نقطه‌ای که خط مماس از محور x عبور می‌کند، باید تخمین بهتری از ریشه نسبت به x₁ ارائه کند. این نقطه، x₂ نامیده می‌شود.

فیلم آموزش روش های عددی ریشه یابی و حل معادلات و پیاده سازی در متلب MATLAB در فرادرس

کلیک کنید

f(x₂)‎ محاسبه و یک خط مماس در x₂ ترسیم می‌شود.

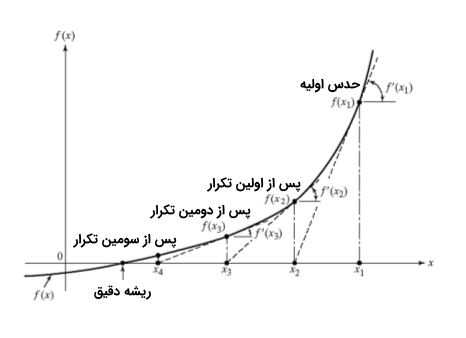
می‌دانیم که شیب خط از (x1, f(x₁))‎ به (x₂, 0) برابر با f'(x₁))‎ است و در آن، f’‎ نشانگر مشتق f است.

f'(x1) = (0 - f(x1)) / (x2 - x1) 

f'(x1) *  (x2 - x1) =  - f(x1)

x2 =  x1 - f(x1) / f'(x1)

با پیدا کردن این نقطه x₂، حرکت به سمت نزدیک‌تر به ریشه، انجام می‌شود. گام بالا باید تا جایی ادامه پیدا کند که به ریشه بسیار نزدیک باشیم یا آن را پیدا کنیم. به طور کلی، داریم:

xn+1 =  xn - f(xn) / f'(xn)

این روش را می‌توان با استفاده از سری تیلور نیز توضیح داد. فرض می‌شود که x₁ حدس اولیه است. می‌توان x₂ را به صورت زیر نوشت.

x_n+1 = x_n + h ------- (1)

در اینجا، h یک مقدار کوچک است که می‌تواند مثبت یا منفی باشد. مطابق با سری تیلور داریم:

فیلم آموزش حل معادلات غیرخطی (رایگان) در فرادرس

کلیک کنید

ƒ(x)‎ که تا بی‌نهایت مشتق‌پذیر است را می‌توان به صورت زیر نوشت.

f(x_n+1) = f(x_{n + h}) = f(x_n) + h*f'(x_n) + ((h*h)/2!)*(f''(x_n)) + ...

با توجه به اینکه هدف پیدا کردن ریشه است، داریم f(x_n+1) = 0.

f(x_n) + h*f'(x_n) + ((h*h)/2!)*(f''(x_n)) + ... = 0

اکنون، با توجه به اینکه h کوچک است، h*h بسیار کوچک خواهد بود. بنابراین، اگر عبارت‌های مرتبه بالاتر نادیده گرفته شوند، داریم:

f(x_n) + h*f'(x_n) = 0

با جایگزینی مقدار h = xn+1 - xn از معادله ۱، داریم:

f(x_n) + (x_n+1 - x_n)*f'(x_n) = 0

x_n+1 = x_n - f(x_n) / f'(x_n)

نکته:

• معمولا از این روش برای بهبود نتایج به دست آمده توسط روش دوبخشی یا روش نابجایی، استفاده می‌شود.
• «روش بابلی» (Babylonian Method) برای ریشه دوم از روش نیوتون رافسون مشتق شده است.