خط تاثیر در تحلیل سازه | روش های رسم نمودار خط تاثیر سازه — به همراه مثال

اگر یک سازه در معرض بارهای زنده یا متحرک قرار داشته باشد، با تغییر مکان منشا بار، پارامترهای بارگذاری نظیر نیروی برشی، لنگر خمشی، نیروی محوری و غیره تغییر میکنند. این تغییرات در هنگام بررسی یک نقطه مشخص از سازه، توسط خط تاثیر نمایش داده میشوند. به عبارت دیگر، خط تاثیر ابزاری برای درک رفتار یک نقطه از سازه، هنگام اعمال بارهای متحرک است. مهندسان و طراحان از این ابزار به همراه نمودارهای عکسالعمل تکیهگاهی، نیروی برشی و گشتاور خمشی برای طراحی تیر یا خرپا در سازههایی مانند پل و ساختمان استفاده میکنند. در این مقاله، روشهای رسم و انواع خط تاثیر در عضوهای باربر سازههای معین استاتیکی را معرفی میکنیم. سپس، چندین مثال را مورد بررسی قرار میدهیم. در انتها نیز، به آموزش اصول رسم خط تاثیر در سازههای نامعین استاتیکی میپردازیم.
تعریف خط تاثیر چیست ؟
«خط تاثیر» (Influence Line)، نموداری است که تاثیر مولفههای بارگذاری در یک نقطه مشخص از سازه را هنگام اعمال بارهای زنده یا متحرک نمایش میدهد. هنگام بررسی بار مرده (وزن سازه)، پیشبینی عکسالعمل عضوهای سازه در نقاط مختلف نسبتا ساده است؛ زیر مقدار بارهای مرده ثابت است و با گذشت زمان تغییر نمیکند.
در طرف مقابل، شرایط برای بارهای زنده نظیر وزن انسان یا خودرو (اجسام متحرک) متفاوت است؛ چراکه مقدار این بارها در طول زمان تغییر میکند. از اینرو، بررسی و پیش بینی عکسالعملهای بحرانی نقاط مختلف عضوهای سازه، میزان تمرکز تنش و نحوه توزیع بارها در هنگام اعمال بارهای زنده، نسبتا پیچیده و دشوار میشود. در نتیجه باید از یک روش مطمئن برای پیش بینی شرایط بارگذاری در نقاط مختلف سازه استفاده کرد.

خط تاثیر، مولفههای بارگذاری نظیر نیروی برشی، لنگر خمشی یا عکسالعمل در یک نقطه مورد بررسی از عضوهای باربر سازه مانند تیر و خرپا را نمایش میدهد. ترسیم این نمودار به طراح کمک میکند تا محل قرار دادن بار زنده برای محاسبه حداکثر نیروی برشی یا لنگر خمشی تیر را به دست آورد. توجه داشته باشید که نمودار خط تاثیر برای تعیین تغییر شکل و نیروهای محوری اعمال شده بر تیر نیز قابل استفاده است.
کاربرد خط تاثیر در تحلیل سازه چیست؟
خطوط تاثیر، ابزاری هستند که برای طراحی تیرها و خرپاها در سازههایی نظیر پل، جرثقیل سقفی، نوار نقاله، شاهتیر کف ساختمان و دیگر سازههای تحت تاثیر بارهای متحرک (در راستای دهانهشان) مورد استفاده قرار میگیرند.
این خطوط، محل ایجاد عکسالعمل حداکثری با توجه به پارامتر مورد تحلیل (نیروی برشی، لنگر خمشی، عکسالعمل، نیروی محوری، تغییر شکل و غیره) را نمایش میدهند. خطوط تاثیر علاوه بر تعیین حداکثر تاثیر بار متحرک در هر نقطه، برای محاسبه حداکثر تاثیر بار متحرک در نقطه بحرانی (ماکسیمم مطلق) نیز کاربرد دارند.
انواع خط تاثیر در تحلیل سازه
انواع خطوط تاثیر به پارامتر مورد بررسی (نیروی برشی، لنگر خمشی، عکسالعمل، نیروی محوری، تغییر شکل) و روش ترسیم (تقریبی یا دقیق) بستگی دارد. در اغلب موارد، یک بار واحد متمرکز به منظور ترسیم این خطوط مورد استفاده قرار میگیرد. به همین دلیل، اکثر خطوط تاثیر، مقیاسی از خطوط تاثیر واقعی را نمایش میدهند. اگرچه، این خطوط، اسکالر و افزایشی هستند. به عبارت دیگر، امکان استفاده از خط تاثیر برای تحلیل تاثیر بارهای غیر واحد و چندین بار وجود دارد. به منظور تعیین تاثیر بارهای غیر واحد، نتایج به دست آمده از خطوط تاثیر در بارهای واقعی ضرب میشوند. به این ترتیب، تمام طول این خطوط یا فقط مقادیر حداکثری و حداقلی آنها را میتوان به مقیاس واقعی تبدیل کرد. مقادیر حداکثری و حداقلی خطوط تاثیر، اعداد مهمی هستند که برای طراحی تیر یا خرپا مورد استفاده قرار میگیرند.
تفاوت خط تاثیر با نمودارهای نیروی برشی و گشتاور خمشی چیست؟
خط تاثیر، اثر بار متحرک بر روی یک نقطه مشخص از دهانه سازه را نمایش میدهد. در صورتی که نمودارهای نیروی برشی و گشتاور خمشی، ابزاری برای نمایش تاثیر بار مرده (بار ثابت) بر روی تمام نقاط در دهانه عضو باربر هستند.
حداکثر تاثیر بار متحرک بر سازه چگونه محاسبه میشود؟
هنگامی که خطوط تاثیر عکسالعمل، نیروی برشی و لنگر خمشی برای یک نقطه از سازه رسم شدند، حداکثر تاثیر نیروی متمرکز متحرک با ضرب بیشترین ارتفاع خط تاثیر در مقدار نیرو محاسبه میشود. در بخشهای بعدی، مبانی تعیین حداکثر تاثیر بار متحرک را با مثال توضیح خواهیم داد.
روش های رسم خط تاثیر کدام هستند؟
رسم خطوط تاثیر عکسالعمل، نیروی برشی، لنگر خمشی یا نیروی محوری در یک نقطه مشخص بر روی دهانه سازه، معمولا با استفاده از روش ایجاد جدول یا روش معادله خط تاثیر انجام میشود. البته، یک روش سریع بر اساس اصل مولر-برسلاو نیز برای این کار وجود دارد که شکل تقریبی خط تاثیر را تعیین میکند. در ادامه به معرفی اصول هر یک از این روشها میپردازیم.
رسم خط تاثیر با روش جدول
به منظور رسم خطوط تاثیر با استفاده از روش «جدول بندی مقادیر» (Tabulate Values)، باید نکات زیر را مد نظر قرار داد:
- اعمال نیروی واحد در نقاط مختلف عضو مورد تحلیل (فاصله x از مبدا فرضی) و استفاده از اصول استاتیک برای تعیین پارامتر مورد نظر (عکسالعمل، نیروی برشی یا لنگر خمشی) در آن نقاط
- فرض مثبت بودن عکسالعمل در جهت رو به بالا، هنگام ترسیم خط تاثیر نیروی عمودی عکسالعمل در یک نقطه از تیر
- فرض مثبت بودن نیروی برشی و گشتاور خمشی مطابق با قواعد علامتگذاری در رسم نمودارهای نیروی برشی و گشتاور خمشی، هنگام ترسیم خط تاثیر این پارامترها
- مستقیم بودن تمام بخشهای خطوط تاثیر در اعضای معین استاتیکی
- تشکیل جدول بار واحد در نقطه x نسبت به پارامتر محاسبه شده در نقطه مورد بررسی، به منظور جلوگیری از خطاهای احتمالی
- ترسیم نقاط مختلف خط تاثیر با توجه به مختصات به دست آمده از جدول
توجه داشته باشید که با تکرار و تمرین میتوان نقاط انتهایی (تغییر روند خط تاثیر) را به سرعت تشخیص داد و مقادیر پارامترهای مورد بررسی را در نقاط محاسبه کرد. این کار، میزان محاسبات مورد نیاز برای ترسیم خطوط تاثیر را کاهش میدهد. در بخش مثالها، نحوه به کارگیری اصول بالا را نمایش خواهیم داد.
رسم خط تاثیر به روش معادلات خط تاثیر
یکی دیگر از روشهای رسم خطوط تاثیر، قرار دادن نیروی واحد در یک موقعیت متغیر (x) بر روی عضو باربر و محاسبه مقادیر عکسالعمل (R)، نیروی برشی (V) و گشتاور خمشی (M) برای نقطه مورد بررسی به صورت تابعی از x است. به این ترتیب، امکان ترسیم بخشهای مختلف خط تاثیر با استفاده از معادلات به دست آمده فراهم میشود. به کارگیری این روش، نیازمند آشنایی مناسب با نحوه تعیین پارامتریک عکسالعمل، نیروی برشی و گشتاور خمشی است. در صورت عدم آشنایی کافی با این مباحث، مطالعه مقالات زیر را به شما پیشنهاد میکنیم:
- عکسالعملهای تکیهگاهی در تیرها – به زبان ساده
- نیروی برشی و گشتاور خمشی در تیرها – به زبان ساده
- نمودار نیروی برشی و گشتاور خمشی – آموزش جامع
رسم خط تاثیر با SAP
یکی از سادهترین روشهای رسم خط تاثیر و تحلیل سازههای تحت بارهای متحرک، استفاده از نرم افزارهای مهندسی عمران و سازه نظیر نرم افزار SAP2000 است.
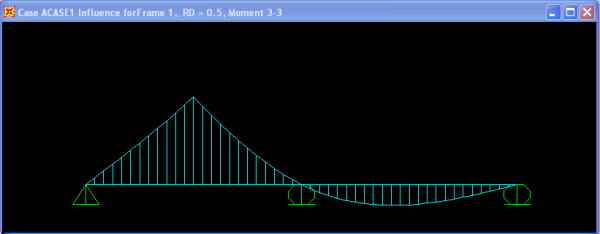
نرم افزار سپ 2000، امکان مدلسازی المانهای سازه و اجرای تحلیلهای متنوع را فراهم میکند. علاوه بر این، کاربر میتواند پس از تعیین مشخصات بارگذاری، با انتخاب گزینه «Influence Line»، خط تاثیر نیروی برشی، لنگر خمشی و نیروی محوری را مشاهده کند.
رسم خط تاثیر به روش مولر-برسلاو
در سال 1886 میلادی (1264 شمسی)، «هنریخ مولر-برسلاو» (Heinrich Muller Breslau)، روشی را برای ترسیم سریع شکل خط تاثیر ارائه داد. این روش با عنوان «اصل مولر-برسلاو» (Müller Breslau's Principle) شناخته میشود. بر اساس این اصل، مقیاس خط تاثیر یک پارامتر با مقیاس شکل جابجایی تیر در هنگام اعمال آن پارامتر یکسان است.
به منظور رسم صحیح شکل جابجایی، باید ظرفیت نقطه مورد بررسی برای مقاومت در برابر پارامتر اعمال شده را نادیده گرفت تا تیر بتواند آزادانه، تحت تاثیر آن پارامتر جابجا شود. در واقع، این روش از اصل کار مجازی برای ترسیم خط تاثیر استفاده میکند. روند تحلیل در روش مولر-برسلاو به صورت زیر است:
- حذف قید در نقطه مورد نظر برای پارامتر مورد بررسی
- فرض صلبیت بینهایت بخش باقیمانده المان مورد تحلیل
- دوران یا جابجایی بخش آزاد در راستای مثبت به اندازه یک واحد
برای درک بهتر مراحل بالا، تصویر زیر را در نظر بگیرید.

در صورت نیاز به ترسیم خط تاثیر برای عکسالعمل عمودی در A، ابتدا باید قید تکیهگاه را برای این پارامتر حذف کرد. به این منظور، قرار دادن یک غلتک به جای تکیهگاه میتواند گزینه مناسبی برای این کار باشد. دلیل استفاده از غلتک این است که تکیهگاه باید در برابر بارهای افقی مقاومت کند اما نیازی به مقاومت آن در برابر بارهای عمودی (مانند عکسالعمل عمودی A) نیست؛ چراکه در این مثال، هدف از ترسیم خط تاثیر، مشاهده عکسالعمل عمودی است. به این ترتیب، اگر یک بار مثبت (رو به بالا) بر نقطه A اعمال شود، تیر مطابق با خطچین نمایش داده شده در تصویر زیر جابجا میشود.
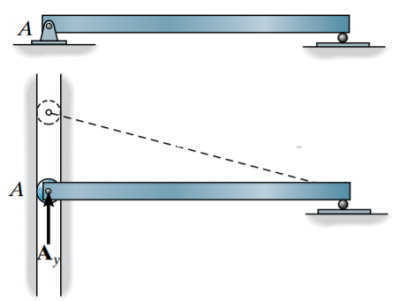
مطابق با اصل مولر-برسلاو، خط جابجایی تیر در تصویر بالا، شکل کلی خط تاثیر برای Ay (عکسالعمل عمودی A) در نقطه A را نمایش میدهد. در مثال 1 (بخش مثالها)، نحوه محاسبه مقادیر عددی برای این حالت توضیح داده شده است. در صورت نیاز به ترسیم خط تاثیر نیروی برشی در نقطه دلخواه (مانند نقطه C در تصویر زیر)، قید این بخش از تیر را باید به صورت غلتک در نظر گرفت. استفاده از غلتک در نقطه میانی تیر باعث از بین رفتن مقاومت آن نقطه در برابر نیروی برشی میشود. این پیکربندی، امکان جابجایی تیر در نقطه C را مطابق با جهت نیروی برشی اعمال شده فراهم میکند. با اعمال نیروی برشی مثبت به تیر در نقطه C و اجازه به جابجایی تیر مطابق با این نیرو، شکل کلی خط تاثیر به دست میآید.
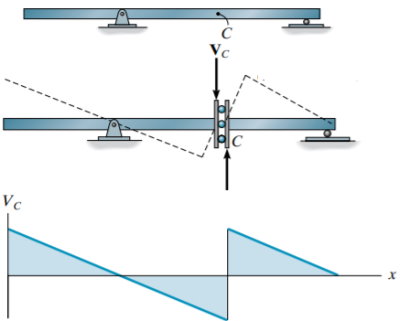
در نهایت به منظور ترسیم شکل خط تاثیر برای گشتاور خمشی در یک نقطه دلخواه، تیر نمایش داده شده در تصویر زیر را در نظر بگیرید. به این منظور، قید تیر در نقطه C را حذف میکنیم و به جای آن یک مفصل قرار میدهیم. این مفصل در برابر نیروهای محوری و برشی مقاومت میکند اما هیچ مقاومتی در برابر گشتاور خمشی ندارد. از اینرو، در صورت اعمال گشتاور MC، تیر مطابق با خطچینهای تصویر زیر جابجا خواهد شد. این خطچینها، شکل کلی خط تاثیر را نمایش میدهند.
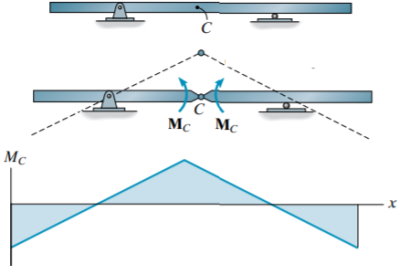
اثبات اصل مولر-برسلاو با استفاده از قضیه کار مجازی صورت میگیرد. اگر یک جسم صلب در حالت تعادل باشد، جمع تمام نیروها و گشتاورهای اعمال شده بر آن برابر با صفر خواهد بود. به همین ترتیب، در صورت اعمال کار مجازی نیز باید مجموع تمام نیروها و گشتاورها برابر با صفر باشد. این توضیحات، مبنای اصل مولر-برسلاو هستند. البته در این بخش به اثبات این اصل نمیپردازیم و فقط تعدادی مثال تصویری را برای تشخیص بهتر شکل خط تاثیر پارامترهای بارگذاری در تیرهای متداول ارائه میکنیم.

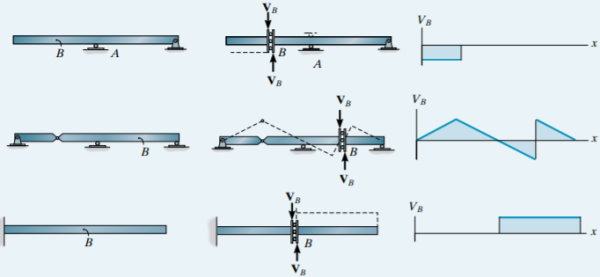
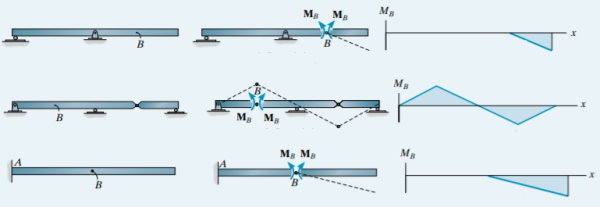
خط تاثیر اعضای سازه ای
خط تاثیر، در اغلب موارد به منظور تحلیل و طراحی اعضای باربر نظیر تیر، شاهتیر و خرپا مورد استفاده قرار میگیرد. در این بخش، به معرفی مفاهیم مرتبط با رسم خطوط تاثیر هر یک از این اعضای سازهای میپردازیم.
خط تاثیر تیر
تیرها یا شاهتیرها، از اصلیترین المانهای باربر در سیستم کف ساختمان یا عرشه پل هستند. از اینرو، رسم خطوط تاثیر این المانها، اهمیت بسیار زیادی در تحلیل سازههای مذکور (ساختمان و پل) دارد. با رسم خط تاثیر عکسالعمل، نیروی برشی یا لنگر خشمی، امکان یافتن محل ایجاد بیشترین مقدار هر یک از این پارامترها بر روی تیر فراهم میشود. برای ترسیم خطوط تاثیر معمولا دو نوع نیرو (متمرکز و گسترده) مورد بررسی قرار میگیرند.
نیروی متمرکز در خط تاثیر تیر
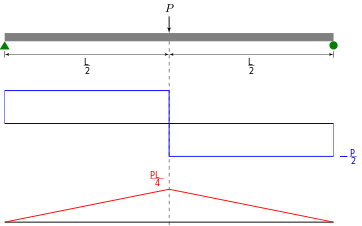
مقادیر عددی پارامترهای خط تاثیر با استفاده از بار واحد (بدون بعد) تعیین میشوند. از اینرو، برای یک بار متمرکز (F) اعمال شده بر روی تیر در هر نقطه (x)، مقدار پارامتر مورد نظر از ضرب ارتفاع خط تاثیر در موقعیت x بر مقدار F به دست میآید. به عنوان مثال، خط تاثیر عکسالعمل تکیهگاه A برای تیر نمایش داده شده در تصویر زیر را در نظر بگیرید.
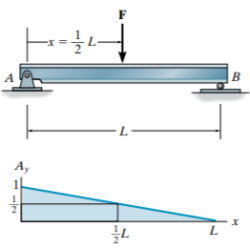
اگر بار واحد در موقعیت x=L/2 قرار داشته باشد، عکسالعمل تکیهگاه A برابر با Ay=1/2 خواهد بود. این نتیجهگیری با استفاده از اصول ساده هندسی به دست آمده است. بنابراین، در صورت قرارگیری نیروی F در موقعیت مذکور، عکسالعمل A برابر با Ay=(1/2)(F) خواهد بود. البته این مقدار با استفاده از اصول استاتیک نیز قابل تعیین است. در هر صورت، حداکثر عکسالعمل ناشی از اعمال F، هنگامی رخ میدهد که این بار بر روی موقعیت حداکثری خط تاثیر قرار داشته باشد. در مثال بالا، این موقعیت برابر با x=0 و عکسالعمل حداکثری برابر با Ay=(1)(F) است.
نیروی گسترده در خط تاثیر تیر
به منظور درک اثر اعمال نیروی گسترده بر روی رسم خط تاثیر، تصویر زیر را در نظر بگیرید. هر المان dx از این بار، نیروی متمرکزی معادل با dF=w0dx را بر روی تیر اعمال میکند. اگر dx در موقعیت x با ارتفاع خط تاثیر y قرار داشته باشد، مقدار تابع پارامتر مورد بررسی برابر با (y)(w0dx)=(y)(dF) خواهد بود.

اثر تمام نیروهای متمرکز dF، از انتگرال بر روی طول تیر به دست میآید:
انتگرال عبارت (ydx) برابر با سطح زیر خط تاثیر است. به همین دلیل، مقدار پارامتر (عکسالعمل، نیروی برشی یا گشتاور خمشی) حاصل از اعمال بار گسترده، با حاصلضرب سطح زیر خط تاثیر آن پارامتر در شدت بار گسترده برابر خواهد بود. به عنوان مثال، تیر نمایش داده شده در تصویر زیر و خط تاثیر عکسالعمل عمودی تکیهگاه A برای شدت بار گسترده w0 را در نظر بگیرید.

بر اساس تعریفی که از نحوه محاسبه مقدار پارامترها با توجه به مساحت زیر خط تاثیر داشتم، رابطه زیر برای Ay صادق خواهد بود:
Ay = [(1/2)(1)(L)] w0 = w0L/2
در صورت استفاده از اصول استاتیک نیز به رابطه بالا میرسیدیم.
خط تاثیر شاهتیر
در اغلب ساختمانها، سیستم کف سازه مشابه با تصویر زیر اجرا میشود. در این سیستم، انتقال بارهای اعمال شده بر کف، ابتدا از دال به تیرهای کف، سپس به شاهتیر و در نهایت به ستون انجام میگیرد. مقطع عرضی این سیستم (تصویر راست)، یک مدل ایدهآل با دال یک طرفه و تکیهگاههای ساده را نمایش میدهد.

شاهتیر در سیستم بالا، المان باربر اصلی محسوب میشود. به همین دلیل در برخی از مواقع، مخصوصا ساختمانهای صنعتی، رسم خطوط تاثیر برای گشتاورها و نیروهای اعمال شده بر آن ضروری است. در صورت اعمال بار واحد به سیستم کف، انتقال نیرو فقط از محل اتصال تیرهای کف به شاهتیر انجام میگیرد. این نقاط با عنوان نقاط پهنه و نواحی بین آنها با عنوان پهنه یا «پنل» (Panel) شناخته میشوند. روند رسم خطوط تاثیر برای شاهتیر مانند تیر است. به عنوان مثال، در صورت اعمال بار واحد بر روی دال کف مطابق با تصویر زیر، میتوان ابتدا عکسالعملهای FB و FC بر روی دال را تعیین کرد و سپس، محسبات عکسالعملهای F1 و F2 بر روی شاهتیر را انجام داد.

گشتاور داخلی در نقطه P نیز توسط روش مقاطع به دست میآید. معادله این گشتاور برابر با MP=F1d-FB(d-s) است. با استفاده از روش مشابه، برش داخلی VP نیز تعیین میشود. اگرچه، برش داخلی در پنل BC ثابت است و به محل قرارگیری P در میان محدوده d بستگی ندارد. از اینرو، خطوط تاثیر نیروی برشی در شاهتیرهای کف، به جای هر نقطه برای هر پهنه مشخص میشود. در بخش مثالها، خط تاثیر برش برای یک شاهتیر را رسم خواهیم کرد.
خط تاثیر خرپا
خرپاها، اغلب به عنوان المانهای باربر اصلی در پلها مورد استفاده قرار میگیرند. از اینرو، رسم خطوط تاثیر هر یک از اعضای این المانها، از اهمیت بالایی در طراحی سازه برخوردار است. همان طور که در تصویر زیر مشاهده میکنید، المانهای خرپا به صورت مستقیم یا غیر مستقیم به دیگر المانهای باربر سازه متصل هستند. بار اعمال شده بر روی عرشه پل به ترتیب در تیرکها، تیرهای کف و مفاصل یال پایینی خرپا توزیع میشود. المانهای خرپا فقط تحت تاثیر بارگذاری در مفاصل قرار میگیرند. به همین دلیل، ارتفاع خط تاثیر برای هر المان با اعمال بار واحد بر روی مفاصل در راستای عرشه پل و محاسبه نیروی موجود در المان توسط روش مفاصل و یا روش مقاطع قابل ترسم خواهد بود.

دادههای حاصل از اعمال بار واحد به مفاصل خرپا در یک جدول (بار واحد اعمال شده بر مفصل در برابر نیروی درون عضو) یادداشت میشود. طبق قاعده کلی، نیروی کشش دارای علامت مثبت و نیروی فشاری دارای علامت منفی است. با استفاده از دادههای جمعآوری شده در جدول و رسم خطوط مستقیم بین نقاط، خط تاثیر هر عضو به دست میآید. در بخش مثالها، روند رسم خط تاثیر در یکی از عضوهای خرپا را نمایش خواهیم داد.
کاربرد خط تاثیر
خط تاثیر، ابزاری است که به منظور تعیین حداکثر تاثیر بار متمرکز یا گسترده متحرک بر روی یک نقطه از دهانه سازه مورد استفاده قرار میگیرد. این ابزار در محاسبه حداکثر بارهای اعمال شده به نقاط بحرانی سازه نیز کاربرد دارد. در اغلب موارد، خط تاثیر با در نظر گرفتن یک بار متمرکز ترسیم میشود. با این وجود، در شرایط واقعی، دهانه سازه معمولا تحت چندین بار متمرکز یا گسترده قرار دارد. در ادامه، نحوه بررسی این شرایط را توضیح میدهیم.
حداکثر تاثیر چند بار متمرکز متحرک
در برخی از موارد، چندین بار متمرکز متحرک بر روی سازه اعمال میشوند. عبور وسایل نقلیه از روی پل، بهترین مثال برای درک این شرایط بارگذاری است. به منظور محاسبه حداکثر تاثیر بارهای متحرک میتوان از روش آزمون و خطا یا روش مبتنی بر تغییرات عکسالعمل، نیروی برشی و لنگر خمشی استفاده کرد. به عنوان مثال، تیر ساده نمایش داده شده در تصویر زیر و خط تاثیر نیروی برشی در نقطه C را در نظر بگیرید.

همانطور که مشاهده میکنید، سه بار متمرکز در حال نزدیک شدن و عبور بر روی تیر بالا از سمت راست به چپ هستند. مطابق با خط تاثیر برش در هنگام اعمال یک بار متمرکز متحرک، حداکثر نیروی برشی در نقطه C، هنگام قرارگیری نیرو بر روی آن نقطه رخ میدهد (به طور دقیقتر، حداکثر نیروی برشی در لحظه پیش از عبور بار از نقطه C رخ خواهد داد). در نتیجه، برای بررسی حداکثر تاثیر اعمال سه بار متمرکز میتوانیم سه سناریوی احتمالی را به صورت آزمون و خطا مورد بررسی قرار دهیم. در سناریوی اول، حداکثر تاثیر زمانی رخ میدهد که بار متمرکز سمت چپ (بار 1 کیلونیوتنی) بر روی نقطه C قرار گیرد.
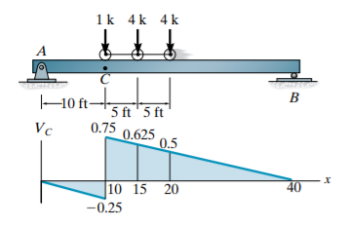
با توجه به خط تاثیر برش خواهیم داشت:
(VC)1 = (1)(0.75) + (4)(0.625) + (4)(0.5) = 5.25 k
در سناریوی دوم، حداکثر تاثیر زمانی رخ میدهد که بار متمرکز سمت وسط (4 کیلونیوتن) بر روی نقطه C قرار گیرد.
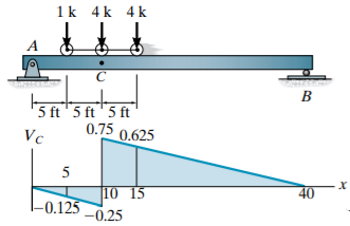
(VC)2 = (1)(-0.125) + (4)(0.75) + (4)(0.625) = 5.375 k
در سناریوی دوم، حداکثر تاثیر زمانی رخ میدهد که بار متمرکز سمت راست (۴ کیلونیوتن) بر روی نقطه C قرار گیرد.
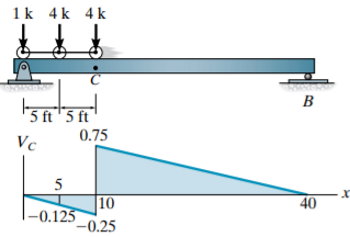
(VC)3 = (1)(0) + (4)(-0.125) + (4)(0.75) = 2.5 k
نتایج به دست آمده از سه سناریوی فرضی نشان میهند که حداکثر مقدار نیروی برشی در نقطه C، هنگام قرارگیری بار متمرکز وسط بر روی این نقطه رخ میدهد. از اینرو، باید مقدار 5.375 کیلونیوتن را به عنوان نیروی برشی بحرانی برای طراحی تیر در نظر گرفت. این رویکرد برای تحلیل مسائلی با تعداد بارهای متمرکز کم نسبتا مناسب است. با این وجود، در صورت اعمال تعداد زیادی از بارهای متمرکز (مانند تصویر زیر)، روش آزمون خطا بسیار وقتگیر و پیچیده میشود. تصویر زیر، عبور قطار از روی یک سازه را نمایش میدهد. تعداد چرخها (نقاط اعمال نیرو) در این حالت به اندازهای زیاد است که نمیتوان به سادگی تاثیر هر یک از آنها را محاسبه و با یکدیگر مقایسه کرد. از اینرو، محل بحرانی بارها با استفاده از تعیین مستقیم نحوه تغییر برش بین سناریوهای مختلف مشخص میشود.

اختلاف نیروی برشی دو سناریوی متوالی در روش محاسبه تغییرات را با ΔV نمایش میدهیم. اگر ΔV محاسبه شده، مثبت باشد، نیروی برشی در سناریوی فعلی بزرگتر از سناریوی قبلی است. از اینرو، باید محاسبات را تا زمان منفی شدن ΔV ادامه دهیم. به این ترتیب، برش قبل از ΔV منفی، بیشترین تاثیر را بر روی نقطه مورد بررسی خواهد داشت. برای درک این روش، تیر قبلی با سه بار متمرکز متحرک را در نظر بگیرید. شیب خط تاثیر برابر با 0.025 و مقدار ارتفاع خط در نقطه C برابر با 1 است.

با تغییر سناریو 1 به سناریو 2، ابتدا بار 1 کیلونیوتنی به اندازه 1 واحد در خط تاثیر به سمت پایین جابجا میشود (جهت منفی اعمال بار) و سپس هر سه بار مطابق با شیب خط به سمت بالا حرکت میکنند. در این حالت، اختلاف نیروی برشی به صورت زیر خواهد بود:
به دلیل مثبت بودن اختلاف نیروی برشی،بار بیشتری در سناریو 2 نسبت به سناریوی 1 بر روی نقطه C اعمال میشود. پس باید به سراغ مرحله بعد برویم. مشابه مرحله قبل، اختلاف برش سناریو 2 و سناریو 3 برابر است با:
به دلیل منفی شدن ΔV، مقدار نیروی برشی در سناریو 2، حالت بحرانی بارگذاری (هنگام بررسی نیروی برشی نقطه C) خواهد بود. در نتیجه، کافی است فقط برش در این سناریو را محاسبه کنیم و مقدار آن را به عنوان مبنای طراحی در نظر بگیریم. در صورت رسم خط تاثیر لنگر خمشی، با استفاده از روشهای توضیح داده شده در این بخش میتوان گشتاور بحرانی را نیز محاسبه کرد.
حداکثر نیروی برشی و گشتاور خمشی مطلق
در بخش قبلی، مشاهده کردید که میتوان از خط تاثیر برای پیدا کردن بحرانیترین وضعیت یک نقطه از سازه، هنگام عبور بارهای متحرک استفاده کرد. این کاربرد، امکان تعیین حداکثر تاثیر بارگذاری بر روی بحرانیترین محل سازه را فراهم میکند. به عنوان مثال، حداکثر تاثیر برش و لنگر خمشی در تیر یکسرگیردار، محل تکیهگاه گیردار آن است.
مقادیر به دست آمده از محاسبه تاثیر بارگذاری بر روی این نقطه با عنوان حداکثر نیروی برشی و گشتاور خمشی مطلق برای تیر یکسرگیردار شناخته میشوند. در نتیجه، به منظور تعیین بحرانیترین حالت بارگذاری در تیر باید بحرانیترین محل آن را تعیین کرد و محاسبات توضیح داده شده در بخش قبلی را بر روی آن محل انجام داد. البته چالش اصلی در این حالت، تعیین مقادیر و محل وقوع نیروی برشی و لنگر خمشی ماکسیمم است. نمودارهای نیروی برشی و گشتاور خمشی، ابزار خوبی برای این کار هستند.
مثال های رسم خط تاثیر
در بخشهای قبلی با مبانی، کابردها و روشهای رسم خطوط تاثیر آشنا شدید. در این بخش، رسم این خطوط برای پارامترهای مختلف در سازههای مختلف را با پنج مثال توضیح میدهیم. در بخش بعدی نیز، مبانی رسم خط تاثیر در سازه های نامعین استاتیکی را معرفی خواهیم کرد.
مثال 1: رسم خط تاثیر عکسالعمل عمودی تیر ساده
تیر نمایش داده شده در تصویر زیر را در نظر بگیرید. در این مثال قصد داریم خط تاثیر عکسالعمل عمودی در تکیهگاه A را رسم کنیم.

روش جدولی
برای رسم خط تاثیر به روش جدولبندی مقادیر، یک بار واحد در فاصله x=2.5 ft و x=5 ft از تکیهگاه A را در نظر میگیرم. سپس، مقادیر عکسالعمل عمودی در این تکیهگاه (Ay) را با جمع گشتاورهای حول تکیهگاه B محاسبه میکنیم. برای x=2.5 ft خواهیم داشت:
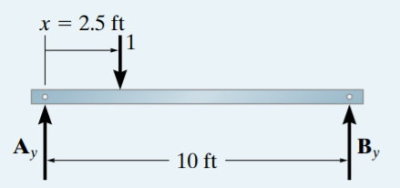
برای x=5 ft نیز داریم:
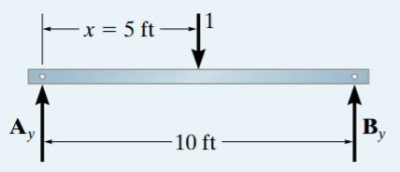
با توجه به مقادیر به دست آمده، جدول زیر را تشکیل میدهیم:
| Ay | x |
| 1 | 0 |
| 0.75 | 2.5 |
| 0.5 | 5 |
| 0.25 | 7.5 |
| 0 | 10 |
از مقادیر جدول بالا برای رسم خط تاثیر عکسالعمل عمودی تکیه A استفاده میکنیم:
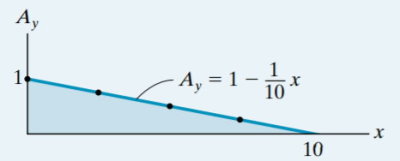
معادله نمایش داده شده در تصویر بالا، معادله تغییرات خط تاثیر را نمایش میدهد که میتوان از آن برای تعیین مقادیر عکسالعمل عمودی تکیهگاه در هر نقطه بر روی تیر استفاده کرد. در بخش بعدی، به توضیح نحوه به دست آوردن این معادله میپردازیم.
روش معادله خط تاثیر
در روش معادلات خط تاثیر، به جای قرار دادن بار واحد بر روی نقاط مشخص تیر و محاسبه مقادیر Ay برای هر نقطه، بار واحد را در موقعیت متغیر x (فاصله نامشخص) از A قرار میدهیم. به این ترتیب، خواهیم داشت:
با جابجایی متغیرهای رابطه بالا به معادله زیر میرسیم:
با استفاده از معادله بالا میتوانیم خط تاثیر Ay را به سادگی رسم کنیم.
مثال 2: رسم خط تاثیر عکسالعمل عمودی تیر ساده با انتهای آزاد
تصویر زیر، یک تیر ساده با انتهای آزاد را نمایش میدهد. در این مثال، قصد داریم خط تاثیر نیروی محوری عمودی در تکیهگاه B را رسم کنیم. به این منظور، ابتدا یک بار واحد را در فاصله x از تکیهگاه A در نظر میگیریم.
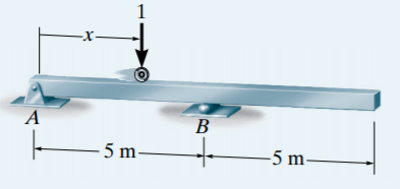
روش جدولی
برای رسم خط تاثیر با استفاده از روش جدولی، بار واحد را بر روی نقاط x=0,2.5,5,7.5,10 اعمال میکنیم و مانند مثال قبل، نیروی محوری عمودی برای هر حالت را با جمع گشتاورها حول نقطه مورد بررسی (نقطه B) به دست میآوریم. جدول زیر، مقدار نیروی محوری عمودی By را نسبت به فاصله بارگذاری x نمایش میدهد.
| By | x |
| 0 | 0 |
| 0.5 | 2.5 |
| 1 | 5 |
| 1.5 | 7.5 |
| 2 | 10 |
با استفاده از اصول استاتیک میتوانید درست بودن مقادیر بالا را تایید کنید. در صورت رسم نقاط جدول و اتصال آنها با خطوط مستقیم، خط تاثیر نیروی محوری عمودی در نقطه B به دست میآید.
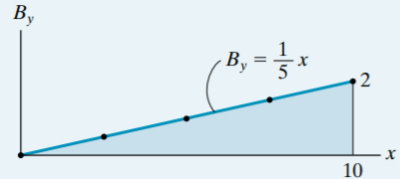
روش معادله خط تاثیر
برای تعیین معادله خط تاثیر باید گشتاور حاصل از بار واحد در فاصله x از A بر روی B را به دست بیاوریم. اگر تکیهگاهها را حذف کنیم و به جای آنها عکسالعمل عمودیشان را قرار دهیم، پیکربندی تیر مشابه تصویر زیر خواهد بود:

با فرض قرارگیری تیر در حالت تعادل، مجموع گشتاورهای حول A برابر است با:
By(5)-1(x)=0
به عبارت دیگر:
By=x/5
این معادله، معادله خط تاثیر نیروی عمودی در نقطه B را نمایش میدهد.
مثال 3: رسم خط تاثیر برش شاهتیر کف ساختمان
در این مثال، قصد داریم خط تاثیر برش در پهنه CD از شاهتیر کف یک سازه را رسم کنیم. پیکربندی شاهتیر مورد بررسی در تصویر زیر نمایش داده شده است.

در این مثال، از روش جدولی با ستونهای x (مقدار فاصله از تکیهگاه A) و VCD (مقدار برش پهنه CD) استفاده میکنیم. به این ترتیب، مقدار VCD در نقاط x=0,10,20,30,40 را به دست میآوریم. تصویر زیر، جزئیات تحلیل برش در نقاط x=0 و x=20 را نمایش میدهد.
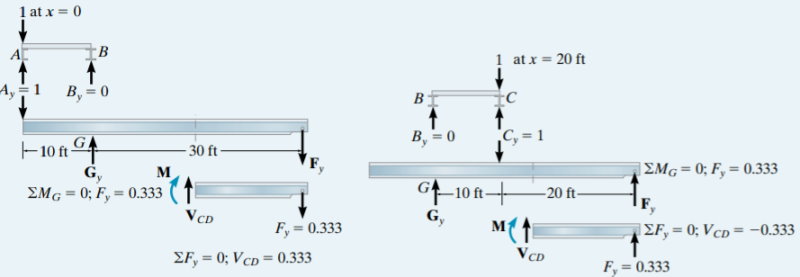
توجه داشته باشید که در هر یک از موارد بالا، ابتدا عکسالعملهای تیرهای کف بر روی شاهتیر (By ،Ay و Cy) محاسبه شدهاند. سپس، عکسالعمل تکیهگاهی شاهتیر در F یا Fy و Gy به دست آمده است. در نهایت، بخشی از شاهتیر در نظر گرفته شده و برش داخلی پهنه VCD مورد محاسبه قرار گرفته است. جدول زیر، مقادیر به دست آماده را نمایش میدهد.
| VCD | x |
| 0.333 | 0 |
| 0 | 10 |
| 0.333- | 20 |
| 0.333 | 30 |
| 0 | 40 |
با رسم نقاط جدول بالا و اتصال آنها توسط خطوط مستقیم، خط تاثیر برای برش در پهنه CD مانند تصویر زیر به دست میآید.

مثال 4: رسم خط تاثیر نیرو در عضو خرپا
خرپای نمایش داده شده در تصویر زیر را در نظر بگیرید. در این مثال، قصد داریم خط تاثیر نیرو در عضو GB این خرپا را رسم کنیم.
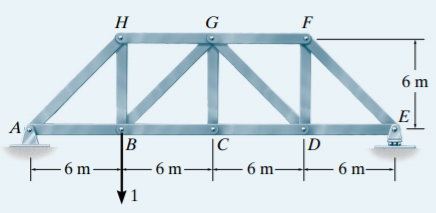
برای حل این مسئله، بار واحد رو به پایین در مفاصل مجاور یال پایینی خرپا (مانند B و C) در نظر گرفته شده و نیروی موجود در عضو GB با استفاده از روش مقاطع تعیین میشود.
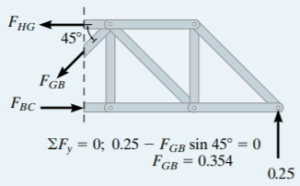
به عنوان مثال، با قرار دادن بار واحد در x=6 (مفصل B)، ابتدا عکسالعمل تکیهگاهی در نقطه E مورد محاسبه قرار میگیرد. سپس، با در نظر گرفتن مقطع عبوری از عضو HG، عضو GB، عضو BC و جدا کردن بخش سمت راست خرپا، نیروی موجود در GB به دست میآید. این روند تا تکمیل جدول زیر برای تمام مفاصل یال پایینی تکرار میشود.
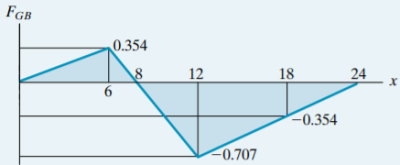
| FGB | x |
| 0 | 0 |
| 0.354 | 6 |
| 0.707- | 12 |
| 0.354- | 18 |
| 0 | 24 |
با رسم نقاط بالا و اتصال آنها توسط خطوط مستقیم، خط تاثیر نیرو در عضو GB مشابه تصویر زیر به دست میآید. همان طور که مشاهده میکنید، خط تاثیر تمام طول دهانه خرپا را در برمیگیرد. از اینرو، عضو GB به عنوان یک عضو اصلی در نظر گرفته میشود. عضوهای اصلی خرپا، معمولا بدون وابستگی به محل اعمال بار بر روی عرشه، تحت بارگذاری قرار میگیرند. البته با توجه به خط تاثیر، در فاصله x=8، هیچ نیرویی به عضو GB اعمال نمیشود.
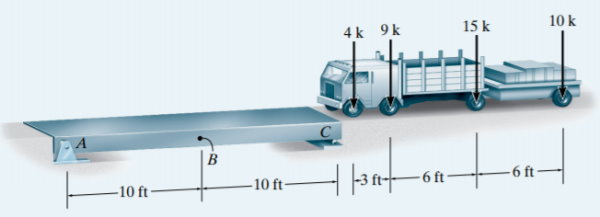
مثال 5: تعیین حداکثر تاثیر نیروی برشی
تصویر زیر، عبور یک کامیون به همراه تریلر متصل به آن از روی یک پل را نمایش میدهد. در این مثال، قصد داریم حداکثر نیروی برشی مثبت در نقطه B هنگام عبور کامیون از روی پل را تعیین کنیم. بارهای متمرکز اعمال شده از طرف چرخها و فواصل مورد نیاز برای انجام محاسبات مطابق با تصویر زیر هستند.
تصویر زیر، خط تاثیر نیروی برشی در نقطه B را نمایش میدهد.
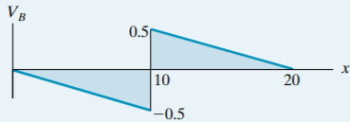
برای شروع محاسبات، محل اعمال بار 4 کیلونیونی را دقیقا در سمت راست نقطه B در نظر بگیرد. از آنجایی که طول قطعه BC برابر با 10 فوت بوده و بار 10 کیلونیوتنی در فاصله 15 فوتی از بار 4 کیلونیوتنی است، بار 10 کیلونیوتنی در سناریو اول به پل اعمال نمیشود. بار حرکت کامیون به اندازه 3 فوت (سناریو 2)، بار 4 کیلونیوتنی ابتدا به اندازه 1 واحد بر روی خط تاثیر (رو به پایین) جابجا میشود و سپس بارهای 4 کیلونیوتنی، 9 کیلونیوتنی و 15 کیلونیوتنی مطابق با شیب خط تاثیر به سمت بالا حرکت میکنند. تغییرات تنش برشی، هنگام تغییر سناریو 1 به سناریو 2، برابر است با:
با حرکت کامیون به اندازه 6 فوت رو به جلو (سناریو 3)، اختلاف نیروی برشی به صورت زیر میشود:
دقت کنید که در این حالت، بار 10 کیلونیوتنی نیز بر روی پل اعمال خواهد شد. به علاوه، میزان حرکت آن بر روی پل، فقط 4 فوت است. پس باید تاثیر آن را به صورت جداگانه در محاسبات اعمال کنیم. در سناریوی آخر، با حرکت کامیون به اندازه 6 فوت، بار 15 کیلونیوتنی جای خود به بار 10 کیلونیوتنی میدهد. با توجه به فاصله بین بارها و طول قطعه BA، با حرکت کامیون، بار 4 کیلونیوتنی پس از 1 متر و بار 9 کیلونیوتنی پس از 4 متر به طور کامل از روی پل عبور میکنند. با در نظر گرفتن این نکات مهم، تغییرات تنش برشی به صورت زیر خواهد بود:
به دلیل منفی شدن تغییرات، تنش برشی اعمال شده در حالت قرارگیری بار 15 کیلونیوتنی بر روی نقطه B، به عنوان مقدار بحرانی در نظر گرفته میشود. برای محاسبه این تنش از خط تاثیر استفاده میکنیم. به این ترتیب داریم:
این مثال، یکی از سادهترین نمونههای کاربرد خط تاثیر برای حل مسائل واقعی بود. البته به منظور ارزیابی بهتر شرایط واقعی، میتوان حرکت چپ به راست کامیون را نیز در نظر گرفت و مقدار حداکثری را از بین دو تنش برشی به دست آمده انتخاب کرد.
خط تاثیر سازه های نامعین استاتیکی
تحلیل سازههای نامعین استاتیکی پیچیدهتر از سازههای معین است. از اینرو، روند ترسیم خط تاثیر پارامترهای بارگذاری برای نقاط مختلف این سازهها مقداری با روند معرفی شده در بخشهای قبلی تفاوت دارد. برخی از پرکاربردترین روشهای رسم خط تاثیر سازه نامعین استاتیکی عبارت هستند از:
- روش تحلیلی
- اصل مولر-برسلاو
- «اصل برهمنهی» (Superposition Principle) یا روش جمع آثار قوا
- «روش توزیع لنگر» (Moment Distribution Method) یا روش پخش لنگر
- روش عددی
- اصل مولر-برسلاو
- نقطهیابی
همان طور که مشاهده میکنید، اصل مولر-برسلاو در روشهای تحلیلی و عددی (نرم افزاری) کاربرد دارد. در ادامه، مبانی رسم خط تاثیر سازههای نامعین استاتیکی را با استفاده از این اصل توضیح میدهیم. درک این بخش، نیازمند آشنایی کافی با مبانی مقاومت مصالح است.
خط تاثیر عکسالعمل تیر نامعین استاتیکی
تیر نامعین نمایش داده شده در تصویر زیر را در نظر بگیرید. به منظور رسم خط تاثیر برای عکسالعمل تکیهگاه A، باید یک بار واحد را بر روی نقاط مختلف تیر اعمال کرده و عکسالعمل در تکیهگاه A را به دست بیاوریم.
به عنوان مثال، در صورت اعمال بار واحد بر روی نقطه D میتوان عکسالعمل A را با استفاده از روش نیرو تعیین کرده و مقدار به دست آمده را به عنوان ارتفاع خط تاثیر در نظر گرفت.
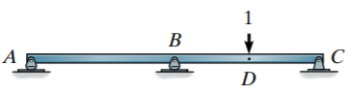
برای تحلیل تیر بالا، از اصل برهمنهی استفاده شده است. تصویر زیر، نحوه به کارگیری این اصل را نمایش میدهد.

معادله سازگاری برای نقطه A به صورت زیر تعریف میشود:
یا
- fAD: جابجایی نقطه A بر اثر اعمال بار در نقطه D
- fAA: جابجایی اضافی بر اثر اعمال عکسالعمل Ay
مطابق با تئوری کار مجازی، fAD=-fDA است. به عبارت دیگر، جابجایی نقطه D بر اثر اعمال عکسالعمل Ay، برابر با جابجایی نقطه A بر اثر اعمال بار واحد در نقطه D است.
به این ترتیب میتوان عکسالعمل Ay یا به عبارت دیگر، ارتفاع خط تاثیر برای عکسالعمل Ay در نقطه D را با استفاده از رابطه زیر تعیین کرد:
در روش مولر-برسلاو، ابتدا باید قید تیر در نقطه A را حذف کرده و سپس بار واحد عمودی را به تیر اعمال کرد. منحنی تغییر شکل به دست آمده در این روش، مشابه تصویر بالا اما با مقیاس 1 بر fAA خواهد بود.
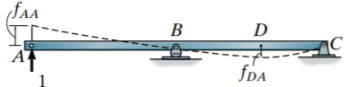
خط تاثیر نیروی برشی تیر نامعین استاتیکی
تیر نامعین نمایش داده شده در تصویر زیر را در نظر بگیرید. به منظور رسم خط تاثیر برای نیروی برشی در نقطه E با استفاده از روش مولر برسلاو، باید تیر را از نقطه مذکور برش دهیم. برای این کار، فرض کنید یک قطعه مخصوص در نقطه E تعبیه شده است که میتواند گشتاور خمشی و نیروی محوری را انتقال دهد.
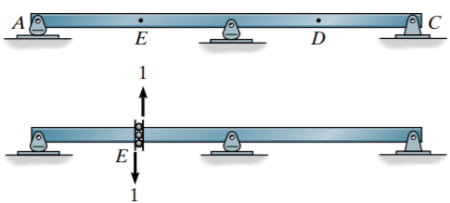
هنگام جابجایی تیر در اثر اعمال بارهای برشی مثبت بر نقطه E، شیب جابجایی در دو طرف قطعه، مانند تصویر زیر ثابت باقی میماند. منحنی جابجایی، خط تاثیر نیروی برشی در نقطه E را با یک مقیاس مشخص نمایش میدهد.

بعد از به کارگیری روشهای اولیه برای ترسیم خط تاثیر، باید بار واحد را بر روی نقاط دیگر (مانند نقطه D) اعمال کرد و نیروی برشی داخلی نقطه E را به دست آورد. مقدار نیروی برشی حاصل از اعمال بار در هر نقطه، ارتفاع خط تاثیر در همان نقطه خواهد بود. با استفاده از روش نیرو و روش کار مجازی (مانند بخش قبلی)، میتوان به رابطه زیر رسید:
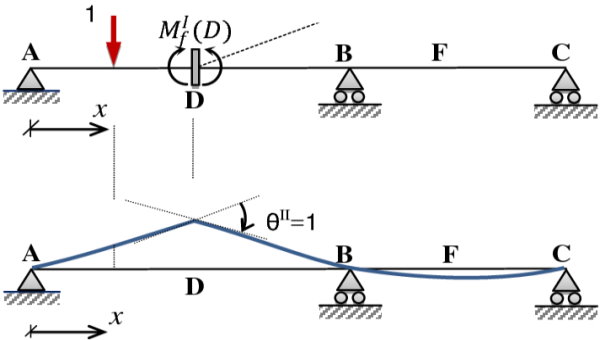
خط تاثیر لنگر خمشی تیر نامعین استاتیکی
تیر نامعین نمایش داده شده در تصویر زیر را در نظر بگیرید. برای رسم خط تاثیر لنگر خمشی در نقطه E، باید یک مفصل را در نقطه E در نظر بگیریم. این مفصل، هیچ مقاومتی را در برابر نیروهای برشی و محوری از خود نشان نمیدهد.
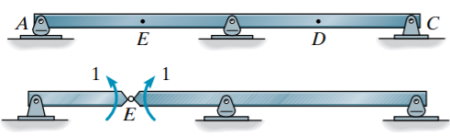
در صورت اعمال لنگر خمشی واحد و مثبت بر روی E، تیر مشابه خطچینهای نمایش داده شده در تصویر زیر جابجا خواهد شد. این جابجایی، با یک نسبت مشخص مشابه با خط تاثیر است.

مطابق با قضیه کار مجازی و روش نیرو داریم:
در مجموع، روش مولر-برسلاو، ابزار کمی و کیفی خوبی را برای ترسیم سریع خط تاثیر سازه های نامعین استاتیکی فراهم میکند.
مثال رسم خط تاثیر با استفاده از روش مولر-برسلاو
تیر ساده زیر را در نظر بگیرید. در نقطه C و فاصله x از تکیهگاه A، یک واحد نیرو به این تیر اعمال شده است. فرض میکنیم این نیرو باعث ایجاد عکسالعملهای RA و RB، به ترتیب در تکیههای A و B میشود.
این شرایط را با عنوان «سیستم شماره 1» در نظر میگیریم. خطچین رسم شده در این سیستم، شکل جابجایی تیر را نمایش میدهد.
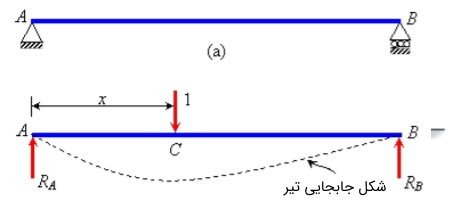
اکنون، قید تکیهگاه A را از درون سیستم حذف میکنیم و به جای آن یک جابجایی واحد مجازی در نظر میگیریم. به این ترتیب، «سیستم شماره 2» با شرایط نمایش داده شده در تصویر بالا به وجود میآید. خطچین رسم شده در این سیستم، همان تیر قبلی با جابجای ناشی از اعمال عکسالعمل RA است.
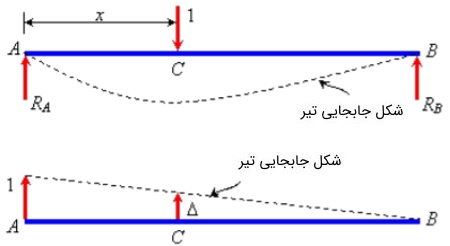
بر اساس قضیه کار مجازی، کار انجام شده توسط نیروها در سیستم شماره 1 با توجه به جابجاییهای سیستم شماره 2 باید با کار انجام شده توسط نیروها در سیستم شماره 2 با توجه به جابجاییهای سیستم شماره 1 برابر باشد. به این ترتیب، برای این دو سیستم میتوان نوشت:
(RA)(1)+(1)(-Δ)=0
سمت راست معادله بالا برابر با صفر است؛ چراکه هیچ جابجایی معادلی برای نیروی عکسالعمل RB وجود ندارد. علامت منفی پشت Δ، جابجایی در خلاف جهت نیروی اعمال شده را نمایش میدهد. با حل معادله بالا خواهیم داشت:
RA=Δ
به عبارت دیگر، عکسالعمل تکیهگاه A به دلیل بار اعمال شده بر نقطه C، با جابجایی نقطه C هنگام اعمال یک واحد جابجایی به سازه در جهت عکسالعمل تکیهگاه A برابر است. با استفاده از این روش میتوان بار واحد را در نقاط دیگر اعمال کرد و عکسالعمل تکیهگاهی ناشی از اعمال آن بار در سیستم شماره 2 را به دست آورد. بنابراین، الگوی جابجایی تیر در سیستم شماره 2، همان خط تاثیر RA را نمایش میدهد.
با تکرار مراحل بالا، امکان رسم خط تاثیر برای هر پارامتر دیگری فراهم میشود. به عنوان مثال، فرض کنید هدف ما ترسیم خط تاثیر نیروی برشی و گشتاور خمشی در نقطه C از یک تیر ساده (تصویر زیر) است. به این منظور، ابتدا یک واحد نیروی رو به پایین را در نقطه D (نقطه دلخواه) به تیر اعمال کرده و قید تیر در نقطه C را حذف میکنیم. به این تریب، تیر به دو بخش AC و CB تقسیم میشود. این شرایط بارگذاری را به عنوان سیستم شماره 1 در نظر میگیریم.

با توجه به سیستم شماره 1، دو نیروی VC در نقطه C و خلاف جهت یکدیگر به تیر اعمال میشوند. یک واحد جابجایی ناشی از این نیروهای برشی را در نقطه C به بخشهای AC و CB اعمال میکنیم. به این ترتیب، سیستم شماره 2 مطابق با تصویر زیر خواهد بود. توجه داشته باشید که جابجایی در نقطه C به گونهای اعمال میشود که هیچ دوران نسبی بین AC و CB وجود نداشته باشد. این فرض برای جلوگیری از انجام هر گونه کار مجازی ناشی از گشتاور MC است.
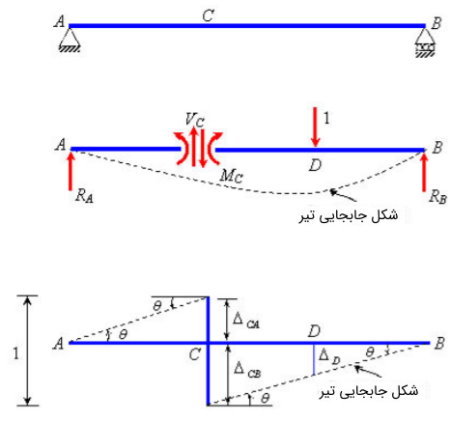
اکنون بر اساس قضیه کار مجازی داریم:
(VC)(ΔCA+ΔCB)+(1)(-ΔD)=0
(VC)(1)-ΔD=0
VC=ΔD
به عبارت دیگر، نیروی برشی ایجاد شده در نقطه C یا VC بر اثر اعمال یک واحد نیرو در نقطه D، با جابجایی نقطه D در اثر اعمال یک واحد جابجایی به نقطه C برابر است. از اینرو، خطچین تغییر شکل در سیستم شماره 2، خط تاثیر نیروی برشی VC را نمایش میدهد. به همین صورت، برای ترسیم خط تاثیر گشتاور خمشی MC، باید یک واحد دوران را در نقطه C (دوران نسبت به AC و CB) اعمال کنیم. اگرچه، به منظور جلوگیری از ایجاد کار مجازی ناشی از VC، نیازی به جابجای نسبی بین AC و BC (مانند حالت قبل) نخواهد بود.

به این ترتیب، بر اساس قضیه کار مجازی خواهیم داشت:
(MC)(θCA+θCB)+(1)(-ΔD)=0
(MC)(1)-ΔD=0
MC=ΔD
خطچین سیستم شماره 2 برای گشتاور خمشی، خط تاثیر گشتاور خمشی MC را نمایش میدهد.











با سلام اشکال مورد استفاده در متن با استفاده از چه نرم افزار هایی رسم میشوند؟
با سلام و وقت بخیر؛
اغلب نرمافزارهای گرافیکی، امکان رسم این نوع شکلها را فراهم میکنند. برای یافتن نرمافزار مناسب، بررسی «مجموعه آموزش فتوشاپ، طراحی و گرافیک کامپیوتری» را به شما پیشنهاد میکنیم.
از همراهیتان با مجله فرادرس سپاسگزاریم