نمودار نیروی برشی و گشتاور خمشی – آموزش جامع

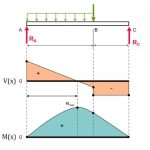
یکی از اطلاعات مهمی که معمولاً در هنگام طراحی‌ها تیرها مورد استفاده قرار می‌گیرد، نحوه تغییرات نیروهای برشی و گشتاورهای خمشی در طول تیر است. در این میان، اطلاعاتی نظیر مقادیر ماکسیمم و مینیمم این کمیت‌ها نیز از اهمیت ویژه‌ای برخوردار هستند. رسم نمودارهای تغییرات نیروی برشی یا گشتاور خمشی نسبت به فاصله نقطه مورد بررسی تا انتهای تیر، اطلاعات مذکور را برای ما فراهم می‌کنند. این نمودارها با عناوین «نمودار نیروی برشی» (Shear Force Diagram) و «نمودار گشتاور خمشی» (Bending Moment Diagram) شناخته می‌شوند. البته در صورت متحرک بودن بار، این نمودارها به همراه خط تاثیر مورد استفاده قرار می‌گیرند. در این مقاله، نحوه رسم و تفسیر نمودارهای نیروی برشی و گشتاور خمشی برای سه حالت بارگذاری (یک بار متمرکز، یک بار گسترده یکنواخت و چندین بار متمرکز) را مورد بررسی قرار خواهیم داد. علاوه بر این، در بخش دوم مقاله نیز برای آشنایی بیشتر با روش‌های تحلیل این حالت‌های بارگذاری، به تشریح چندین مثال متنوع خواهیم پرداخت.

بار متمرکز

تیر ساده زیر را در نظر بگیرید. بار متمرکز P بر روی تیر AB اعمال می‌شود. فاصله این بار تا تکیه‌گاه سمت چپ تیر برابر با a و فاصله آن تا تکیه‌گاه سمت راست برابر با b است.

اگر نمودار جسم آزاد کل تیر را در نظر بگیریم، عکس‌العمل‌های تکیه‌گاهی آن با استفاده از معادلات تعادل به دست می‌آیند:

در مرحله بعد، تیر AB را در فاصله x از تکیه‌گاه A برش می‌دهیم. سپس، نمودار جسم آزاد بخش سمت چپ تیر را مطابق شکل زیر رسم می‌کنیم.

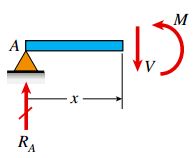
با توجه به معادلات تعادل این جسم آزاد، روابط مورد نیاز برای تعیین نیروی برشی V و گشتاور خمشی M در فاصله x از تکیه‌گاه A به صورت زیر خواهند بود:

این روابط، تنها برای بخش سمت چپ بار P اعتبار دارند. در مرحله بعد، سمت راست بار P (فاصله‌ای بین a تا L) بر روی تیر را برش می‌دهیم. سپس، نمودار جسم آزاد بخش سمت چپ تیر را مطابق شکل زیر رسم می‌کنیم.

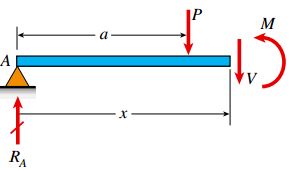
با توجه به معادلات تعادل این جسم آزاد، روابط مورد نیاز برای تعیین نیروی برشی و گشتاور خمشی به دست می‌آیند:

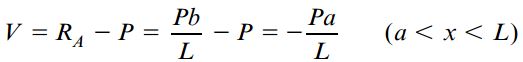
و

توجه داشته باشید که این روابط فقط برای بخش سمت چپ تیر اعتبار دارند. شکل زیر، نمودار نیروی برشی و نمودار گشتاور خمشی تیر AB را نمایش می‌دهد. این نمودارها با استفاده از روابط به دست آمده برای بخش سمت راست و چپ بار متمرکز P رسم شده‌اند.

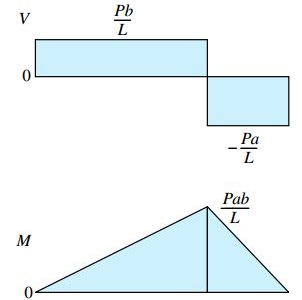
با توجه به نمودار نیروی برشی می‌توان مشاهده کرد که مقدار نیروی برشی در تکیه‌گاه A (فاصله x=0) با مقدار عکس‌العمل R_A برابر است. این نیرو تا رسیدن به نقطه اعمال بار P ثابت باقی می‌ماند. سپس، مقدار آن در نقطه اعمال بار به صورت ناگهانی و به اندازه P کاهش می‌یابد. در بخش سمت راست تیر نیز مانند بخش سمت چپ، میزان نیروی برشی ثابت است اما مقدار عددی آن با عکس‌العمل موجود در نقطه B برابری می‌کند.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

بر اساس نمودار گشتاور خمشی، این گشتاور در سمت چپ تیر از مقدار صفر در تکیه‌گاه A تا مقدار Pab/L در محل اعمال بار متمرکز (فاصله x=a) به صورت خطی افزایش می‌یابد. در بخش سمت راست نیز گشتاور خمشی از مقدار Pab/L در محل اعمال بار تا مقدار صفر در تکیه‌گاه B (فاصله x=L) به صورت خطی کاهش می‌یابد. به این ترتیب، گشتاور خمشی ماکسیمم برابر است با:

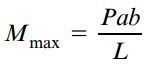
این گشتاور در محل اعمال بار متمرکز رخ می‌دهد. روابط مربوط به تعیین نیروی برشی و گشتاور خمشی موجود در سمت راست محل اعمال بار با توجه به معادلات تعادل جسم آزاد بخش سمت چپ تیر به دست می‌آیند (شکل زیر). این جسم آزاد در معرض نیروهای R_A و P به علاوه V و M قرار دارد. در این مثال بخصوص، استفاده از بخش سمت راست تیر به عنوان جسم آزاد، تحلیل مسئله را ساده‌تر می‌کند؛ چراکه در این حالت تنها یک نیرو (R_B) به علاوه V و M در معادلات تعادل وجود خواهند داشت. توجه داشته باشید که استفاده از هر کدام از این نمودارها (سمت چپ یا راست تیر)، تغییری در نتایج به دست آمده ایجاد نمی‌کند.

اکنون می‌توانیم برخی از ویژگی‌های نمودارهای نیروی برشی و گشتاور خمشی تیر AB را مورد تحلیل قرار دهیم. با توجه به نمودار نیروی برشی، شیب dV/dx در بازه‌های 0 تا a و a تا L برابر با صفر است. این نتیجه با معادله dV/dx=-q مطابقت دارد. بر اساس نمودار گشتاور خمشی، شیب dM/dx در بازه‌های 0 تا a و a تا L با مقدار نیروی برشی V برابری می‌کند. در بخش سمت چپ بار P، شیب نمودار گشتاور خمشی مثبت و برابر با Pb/L است. بخش سمت راست بار، یک شیب منفی با مقدار Pa/L- دارد. به این ترتیب، در محل اعمال بار، نمودار نیروی برشی با یک تغییر ناگهانی (به اندازه P) و نمودار گشتاور خمشی با یک تغییر شیب مواجه می‌شود.

در این مرحله از تحلیل، مساحت زیر نمودار نیروی برشی را مورد بررسی قرار می‌دهیم. در محدوده x=0 تا x=a، مساحت نمودار نیروی برشی برابر با Pab/L است. این کمیت، افزایش گشتاور خمشی به اندازه Pab/L در محدوده مذکور را نمایش می‌دهد. در فاصله x=a تا x=L، مساحت نمودار نیروی برشی با مقدار Pab/L- برابری می‌کند. منفی بودن این مساحت، بیانگر کاهش گشتاور خمشی به اندازه Pab/L- در محدوده مورد بررسی است. در نهایت، گشتاور خمشی در تکیه‌گاه B به مقدار صفر می‌رسد.

اگر گشتاورهای خمشی موجود در هر دو تکیه‌گاه تیر برابر با صفر باشند، مساحت نمودار نیروی برشی در محدوده x=0 تا x=L صفر خواهد بود. معمولاً این حالت را می‌توان در تیرهای ساده‌ای مشاهده کرد که هیچ کوپلی بر روی آن‌ها اعمال نمی‌شود. به خاطر داشته باشید که در طراحی تیرها از مقادیر ماکسیمم و مینیمم نیروهای برشی استفاده می‌شود. برای یک تیر ساده با یک بار متمرکز، نیروی برشی ماکسیمم در تکیه‌گاه نزدیک به محل اعمال بار و گشتاور خمشی ماکسیمم در زیر محل اعمال بار رخ می‌دهد.

بار گسترده یکنواخت

شکل زیر، تیر ساده‌ای را نمایش می‌دهد که تحت یک بار گسترده یکنواخت با شدت q قرار گرفته است. به دلیل متقارن بودن تیر و بار اعمال شده بر روی آن، مولفه‌های عمودی عکس‌العمل‌های تکیه‌گاهی (R_A و R_B) برابر با qL/2 هستند (در این مثال، عکس‌العمل‌های تکیه‌گاهی مولفه افقی ندارند).

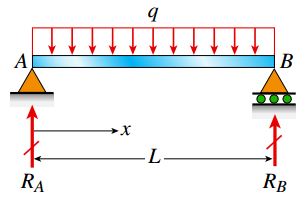
به این ترتیب، روابط مورد نیاز برای تعیین نیروی برشی و گشتاور خمشی موجود در فاصله x از انتهای سمت چپ تیر به صورت زیر خواهد بود:

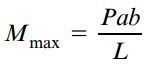
و

معادلات بالا برای تمام طول تیر قابل استفاده هستند. با رسم این معادلات، نمودارهای نیروی برشی و گشتاور خمشی تیر به دست می‌آیند. نمودار نیروی برشی تیر مورد بررسی، از یک خط شیب‌دار مستقیم در محدوده x=0 تا x=L تشکیل می‌شود. مقدار عددی نیروی برشی در نقاط ابتدایی و انتهایی این محدوده با مقدار عکس‌العمل‌های موجود در آن نقاط برابر است. شیب خط نمودار نیز با مقدار q- برابری می‌کند.

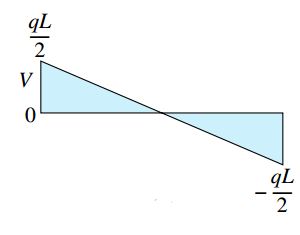
نمودار گشتاور خمشی تیر نیز یک منحنی سهمی‌وار را تشکیل می‌دهد. این منحنی حول مرکز تیر دارای تقارن است. در هر یک از مقاطع عرضی تیر، شیب منحنی گشتاور خمشی با مقدار نیروی برشی در آن مقطع برابر خواهد بود:

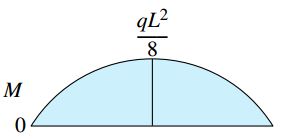
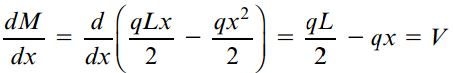
در این مثال، مقدار ماکسیمم گشتاور خمشی در نقطه مرکزی تیر رخ می‌دهد (جایی که dM/dx و نیروی برشی صفر هستند). به این ترتیب، با جایگذاری x=L/2 در رابطه M، خواهیم داشت:

مساحت نمودار شدت بار (شکل زیر) برابر با qL است. از این‌رو، به دلیل برابر بودن مساحت نمودار بارگذاری با VB-VA، با حرکت از نقطه A تا نقطه B، نیروی برشی V به اندازه qL کاهش می‌یابد. در صورت به دست آوردن تفاوت مقادیر نیروهای برشی از روی نمودار نیز همین اختلاف به دست خواهد آمد.

مساحت نمودار نیروی برشی در محدوده x=0 تا x=L/2 برابر با qL²/8 است. این مساحت، میزان افزایش گشتاور خمشی در محدوده مذکور را نمایش می‌دهد. به همین ترتیب، میزان کاهش گشتاور خمشی در محدوده x=L/2 تا x=L برابر با qL²/8 خواهد بود.

چندین بار متمرکز

در صورت اعمال چندین بار متمرکز بر روی یک تیر ساده، روابط مربوط به نیروهای برشی و گشتاورهای خمشی، برای هر یک از نواحی بین محل اعمال بارها تعیین می‌شوند.

اگر نمودار جسم آزاد بخش سمت چپ تیر در فاصله x از انتهای A را رسم کنیم، معادلات زیر برای بخش اول تیر به دست می‌آیند:

معادلات مربوط به بخش دوم تیر نیز به صورت زیر خواهند بود:

برای بخش سوم و چهارم می‌توانیم از نمودار جسم آزاد سمت راست تیر استفاده کنیم. در این حالت، تعداد بارهای اعمال شده بر روی نمودارهای جسم آزاد کم‌تر خواهد بود. به این ترتیب، برای نیروی برشی و گشتاور خمشی بخش سوم خواهیم داشت:

در نهایت، روابط مربوط به تعیین نیروی برشی و گشتاور خمشی در بخش چهارم تیر نیز به صورت زیر خواهند بود:

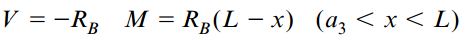
معادلات به دست آمده در این بخش را می‌توان برای رسم نمودارهای نیروی برشی و گشتاور خمشی مورد استفاده قرار داد. شکل زیر، نمودار نیروی برشی تیر مورد بررسی در این بخش را نمایش می‌دهد. بر اساس این نمودار، مقدار نیروی برشی در هر بخش تیر ثابت است و با رسیدن به محل اعمال هر یک از بارهای متمرکز، مقدار این نیرو به صورت ناگهانی و به اندازه بار اعمال شده تغییر می‌کند.

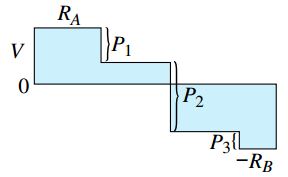
شکل زیر، نمودار گشتاور خمشی تیر مورد تحلیل را نمایش می‌دهد. با توجه به این نمودار، مقدار گشتاور خمشی در هر بخش تیر، یک تابع خطی از فاصله x است. به این ترتیب، نمودار گشتاور خمشی مربوط به هر بخش، یک خط شیب‌دار مستقیم خواهد بود. به منظور رسم این خطوط می‌توانیم مقادیر x=a₂ ،x=a₁ و x=a₃ را در معادلات به دست آمده جایگذاری کنیم و گشتاورهای مربوط به هر بخش را به دست بیاوریم.

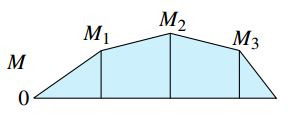
به این ترتیب، خواهیم داشت:

اگر نقاط معرف این مقادیر را توسط خطوط مستقیم به هم وصل کنیم، نمودار گشتاور خمشی کل تیر ایجاد می‌شود (مانند نمودار بالا). برای هر بخش از نمودار نیروی برشی، شیب متناظر dM/dx در نمودار گشتاور خمشی تغییر می‌کند. اختلاف بین گشتاورهای خمشی در فاصله بین دو نقطه بارگذاری با مساحت نمودار نیروی برشی در همان محدوده برابر است. به عنوان مثال، اختلاف بین گشتاورهای خمشی در فاصله P₁ تا P₂، از رابطه M₂-M₁ به دست می‌آید.

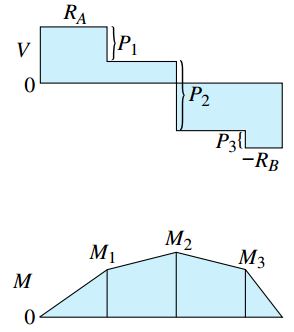
با توجه به روابط به دست آمده برای گشتاورهای خمشی هر بخش، داریم:

این رابطه، مساحت نمودار نیروی برشی در محدوده x=a₁ تا x=a₂ را نمایش می‌دهد. گشتاور خمشی ماکسیمم در تیرهایی که فقط تحت بارهای متمرکز قرار دارند در زیر یکی از این بارها یا یکی از تکیه‌گاه‌ها رخ می‌دهد. به خاطر داشته باشید که شیب نمودار گشتاور خمشی با نیروی برشی برابر است. بنابراین در گشتاورهای خمشی مینیمم یا ماکسیمم، عبارت dM/dx (شیب نمودار گشتاور) و نیروی برشی تغییر علامت می‌دهند. به علاوه، در تیرهایی که فقط تحت بارهای متمرکز قرار دارند، علامت تنش برشی تنها در زیر محل اعمال بار تغییر می‌کند.

فیلم آموزش مقاومت مصالح ۲ + مفاهیم کلیدی در فرادرس

کلیک کنید

اگر در حین حرکت بر روی محور x، نیروی برشی مانند شکل زیر از یک مقدار مثبت به یک مقدار منفی تغییر کند، شیب نمودار گشتاور خمشی تیز از مثبت به منفی تغییر خواهد کرد. این مسئله بیانگر وجود گشتاور خمشی ماکسیمم در این سطح مقطع است. در طرف مقابل، تغییر مقدار نیروی برشی از منفی به مثبت، وجود یک گشتاور خمشی مینیمم را نمایش می‌دهد. از نظر تئوری، نمودار نیروی برشی می‌تواند محور افقی را در چند محل مختلف قطع کند. با این وجود، احتمال رخ دادن چنین حالتی بسیار پایین است. در این صورت، برای هر یک از نقاط تقاطع در نمودار نیروی برشی، یک مقدار مینیمم یا ماکسیمم محلی در نمودار گشتاور خمشی به وجود می‌آید. در نتیجه، به منظور یافتن گشتاورهای خمشی ماکسیمم مثبت و منفی باید تمام مقادیر مینیمم و ماکسیمم محلی را با هم مقایسه کرد.

نکات تکمیلی

عبارت‌های ماکسیمم و مینیمم در اغلب موارد برای بیان مفهوم بزرگ‌ترین و کوچک‌ترین مقدار مورد استفاده قرار می‌گیرند. در نتیجه، صرف نظر از روش رسم نمودار گشتاور خمشی (به کارگیری یک تابع پیوسته هموار یا اتصال چندین خط مستقیم)، عبارت گشتاور خمشی ماکسیمم یک مقدار حداکثری را بیان می‌کند. علاوه بر این نکته، در اغلب موارد باید بین کمیت‌های مثبت و منفی تمایز قائل شد.

به این منظور می‌توان از عبارت‌هایی نظیر گشتاور ماکسیمم مثبت یا گشتاور ماکسیمم منفی نیز استفاده کرد. در هر دو مورد، عبارت گشتاور ماکسیمم مثبت/منفی بیانگر کمیتی با بزرگ‌ترین مقدار عددی است. به عنوان مثال، گشتاور ماکسیمم منفی در واقع بزرگ‌ترین مقدار عددی گشتاور منفی را نمایش می‌دهد. این توضیحات برای کمیت‌های دیگری نظیر نیروی برشی و خمیدگی نیز صادق هستند.

احتمال رخ دادن گشتاورهای خمشی ماکسیمم مثبت و منفی در نقاط زیر وجود دارد:

• سطح مقطعی که تحت بار متمرکز قرار گرفته باشد و نیروی برشی در آن نقطه تغییر علامت دهد.
• سطح مقطعی که نیروی برشی در آن برابر با صفر است.
• تکیه‌گاهی که یک عکس‌العمل عمودی در آن وجود دارد.
• سطح مقطعی که یک کوپل بر روی آن اعمال می‌شود.

توجه: مصادیق هر یک از موارد بالا را می‌توانید در بخش‌های قبلی مشاهده کنید.

در صورت اعمال چندین بار بر روی یک تیر، نمودارهای نیروی برشی و گشتاور خمشی با استفاده از برهم‌نهی (جمع‌بندی) نمودارهای حاصل از هر بخش قابل رسم خواهند بود. به عنوان مثال، نمودار نیروی برشی شکل زیر (اعمال چندین بار متمرکز)، در واقع از جمع سه نمودار مجزا (مانند نمودار اعمال یک بار متمرکز) به دست آمده است. برهم‌نهی نمودارهای نیروی برشی و گشتاور خمشی در تیرهای معین استاتیکی هیچ مانعی ندارد؛ چراکه در این نوع تیرها، رابطه بین نیروهای برشی و گشتاورهای خمشی با بارهای اعمال شده به صورت خطی است.

برنامه‌های کامپیوتری و سایت‌های اینترنتی مختلف (به عنوان مثال skyciv و beamguru)، امکان رسم نمودارهای نیروی برشی و گشتاور خمشی را فراهم می‌کنند. بعد از یادگیری مبانی این نمودارها و نحوه رسم آن‌ها می‌توانید از این ابزارها برای تحلیل مثال‌های عددی استفاده کنید.

^^