رسم نمودار نیروی برشی و گشتاور خمشی – مثال های طبقه بندی شده

در مبحث «نمودار نیروی برشی و گشتاور خمشی»، نحوه رسم و تفسیر نمودارهای نیروی برشی و گشتاور خمشی برای سه حالت بارگذاری (یک بار متمرکز، یک بار گسترده یکنواخت و چندین بار متمرکز) را مورد بررسی قرار دادیم. در بخش دوم این مبحث، به منظور آشنایی بیشتر و بهتر با روشهای تحلیل نمودارهای نیروی برشی و گشتاور خمشی در شرایط مختلف، به تشریح چندین مثال متنوع و طبقهبندی شده (از شرایط ساده تا پیچیده) خواهیم پرداخت.
مثال 1
شکل زیر، تیر سادهای را نمایش میدهد که در معرض یک بار گسترده یکنواخت با شدت q قرار دارد. این بار گسترده فقط به بخشی از تیر اعمال میشود.
با توجه به پیکربندی تیر و اطلاعات مسئله، نمودارهای نیروی برشی و گشتاور خمشی را رسم کنید.

تحلیل این مثال را با تعیین عکسالعملهای تکیهگاهی تیر شروع میکنیم. به این منظور نمودار جسم آزاد کل تیر را در نظر بگیرید.
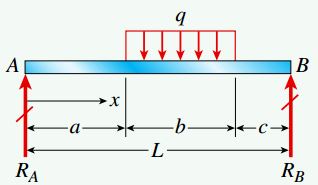
با توجه به نمودار جسم آزاد کل تیر، روابط مورد نیاز برای تعیین عکسالعملهای RA و RB به صورت زیر خواهند بود:
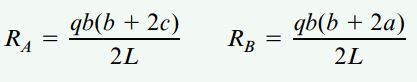
نیروهای برشی و گشتاورهای خمشی
به منظور تعیین نیروهای برشی و گشتاورهای خمشی برای کل تیر باید تیر را به سه بخش مجزا تقسیم کنیم. به این ترتیب، باید ایجاد یک برش برای هر بخش، نیروی برشی V و گشتاور خمشی M درون تیر مشخص میشود. در مرحله بعد، با در نظر گرفتن V و M به عنوان مجهولات مسئله، نمودار جسم آزاد آن بخش تیر را رسم میکنیم (به عنوان نمونه، نمودار جسم آزاد بخش میانی تیر در شکل زیر نمایش داده شده است).
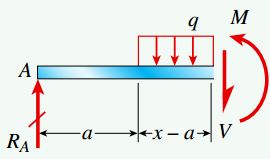
در مرحله آخر، با جمع نیروهای موجود در راستای عمودی، روابط نیروی برشی و با جمع گشتاورهای حول سطح مقطع ایجاد شده، روابط گشتاور خمشی در هر بخش را به دست میآوریم:
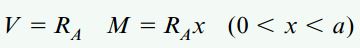
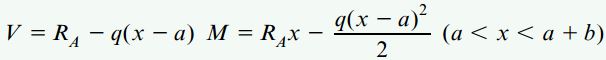
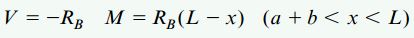
روابط بالا برای محاسبه نیروی برشی و گشتاور خمشی در تمام مقاطع تیر مورد استفاده قرار میگیرند. تمام عبارتهای موجود در این روابط با در نظر گرفتن قاعده علامتگذاری تغییر شکل بیان شدهاند. با توجه به مطالب ارائه شده در مبحث «روابط بین بار، نیروی برشی و گشتاور خمشی در تیرها»، مشتق dV/dx=-q و مشتق dM/dx=V است. با از استفاده از این نکته و مشتق گرفتن از روابط بالا میتوانیم صحت آنها را مورد بررسی قرار دهیم.
نمودارهای نیروی برشی و گشتاور خمشی
در این مرحله، با استفاده از روابط به دست آمده در بخش قبل، نمودارهای نیروی برشی و گشتاور خمشی را مطابق شکلهای زیر رسم میکنیم.
نمودار نیروی برشی دارای خطوط افقی در نواحی بدون بارگذاری و یک خط شیبدار مستقیم (با شیب منفی) در ناحیه بارگذاری است.
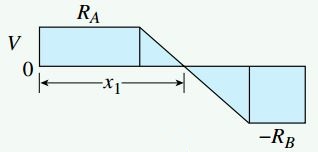
نمودار گشتاور خمشی نیز دو خط شیبدار مستقیم در نواحی بدون بارگذاری و یک منحنی سهمیوار در ناحیه بارگذاری را نمایش میدهد. شیب خطوط مستقیم به ترتیب برابر با RA و RB- است. علاوه بر این، این خطوط شیبدار در نقطه برخورد با منحنی سهمیوار بر آن مماس هستند. توجه داشته باشید که بر اساس قاعده علامتگذاری تغییر شکل، نمودار گشتاور خمشی ناحیه تحت فشار تیر را نمایش میدهد. به این ترتیب، تمام سطح بالایی تیر در معرض فشار قرار دارد. این موضوع با توجه به پیکربندی تیر و نحوه اعمال نیرو قابل پیشبینی بود.
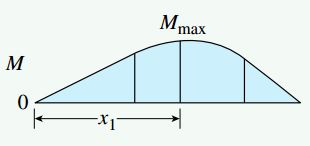
گشتاور خمشی ماکسیمم
گشتاور خمشی ماکسیمم در محلی رخ میدهد که نیروی برشی در آن صفر باشد. اگر روابط به دست آمده برای V (رابطه بخش دوم در این مثال) را برابر با صفر قرار دهیم، محل رخ دادن گشتاور خمشی ماکسیمم مشخص میشود:
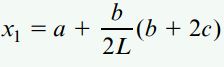
با جایگذاری x1 در رابطه M (رابطه بخش دوم در این مثال)، رابطه گشتاور خمشی ماکسیمم نیز به دست میآید:
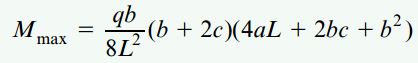
گشتاور خمشی ماکسیمم همیشه در بین ناحیه اعمال بار گسترده رخ میدهد. در یک حالت خاص، اگر بار گسترده به صورت متقارن بر روی تیر اعمال شود (a=c)، روابط بالا به صورت زیر ساده خواهند شد:
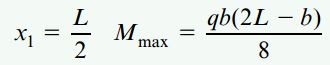
در صورت اعمال بار گسترده بر روی تمام طول تیر، Mmax=qL2/8 خواهد بود.
مثال 2
شکل زیر، تیر یکسر گیرداری را نمایش میدهد که در معرض دو بار متمرکز قرار دارد.
با توجه به پیکربندی تیر و اطلاعات مسئله، نمودارهای نیروی برشی و گشتاور خمشی را رسم کنید.

عکسالعملهای تکیهگاهی
با توجه به نمودار جسم آزاد کل تیر (شکل بالا)، عکسالعمل عمودی RB و گشتاور عکسالعمل MB قابل محاسبه خواهند بود:

توجه: جهت رو به بالا برای نیروی عکسالعمل عمودی و چرخش پادساعتگرد برای گشتاور عکسالعمل به عنوان جهتهای مثبت در نظر گرفته میشوند.
نیروهای برشی و گشتاورهای خمشی
با ایجاد برش در هر یک از بخشهای تیر، رسم نمودارهای جسم آزاد مربوط به آنها و حل معادلات تعادل، امکان تعیین نیروهای برشی و گشتاورهای خمشی فراهم میشود:
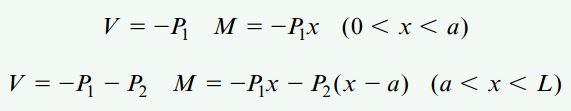
نمودارهای نیروی برشی و گشتاور خمشی
شکلهای زیر، نمودارهای نیروی برشی و گشتاور خمشی را نمایش میدهند. همان طور که مشاهده میشود، نیروی برشی در بین نقاط بارگذاری دارای یک مقدار ثابت است و در محل قرارگیری تکیهگاه به مقدار حداکثری خود (RB) میرسد.

نمودار گشتاور خمشی شامل دو خط راست میشود که شیب هر یک از آنها با نیروی برشی بخش مربوطه برابر است. مقدار حداکثری گشتاور خمشی در تکیهگاه رخ میدهد. این مقدار از نظر عددی با گشتاور عکسالعمل MB و مساحت کل نمودار نیروی برشی برابری میکند.
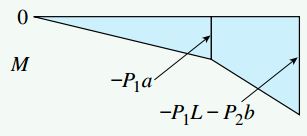
به دلیل ثابت بودن نمودار نیروی برشی در بین نقاط بارگذاری، نمودار گشتاور خمشی در بین این نقاط به صورت خطی است. نمودار گشتاور خمشی، ناحیه تحت فشار تیر را نمایش میدهد (در این مثال سطح زیر تیر). به همین دلیل، سطح بالایی تیر در معرض کشش قرار دارد.
مثال 3
شکل زیر، یک تیر ساده با انتهای آزاد را نمایش میدهد. یک بار گسترده یکنواخت با شدت q=400lb/ft بر روی تمام طول تیر اعمال میشود. علاوه بر این، این تیر در فاصله 9 فوتی از تکیهگاه سمت چپ خود تحت بار متمرکز P=2400lb نیز قرار دارد.
با توجه به پیکربندی تیر و اطلاعات مسئله، ابتدا روابط مورد نیاز برای تعیین نیروی برشی V و گشتاور خمشی M را به صورت تابعی از x (فاصله تا تکیهگاه سمت چپ) به دست آورید. سپس، نمودارهای نیروی برشی و گشتاور خمشی را رسم کنید.

عکسالعملهای تکیهگاهی
برای شروع تحلیل، ابتدا نمودار جسم آزاد کل تیر را مطابق شکل زیر رسم میکنیم. در مرحله بعد، نیروهای عکسالعمل RA و RB را به دست میآوریم. سپس با ایجاد برش در نقطه D، مقدار نیروی برشی VD و گشتاور خمشی MD در این نقطه را مورد محاسبه قرار میدهیم. در این مرحله، تغییرات نیروی برشی V و گشتاور خمشی M بر روی تمام طول تیر قابل محاسبه و رسم خواهد بود. با توجه به اعمال بار متمرکز P و نیروی عکسالعمل RB، توابع معرف نیروی برشی (V(x و گشتاور خمشی (M(x دارای بخشهای جداگانه هستند. از اینرو، به منظور دستیابی به توابع (V(x و (M(x در طول کل تیر باید سه برش جداگانه را مورد بررسی قرار دهیم.
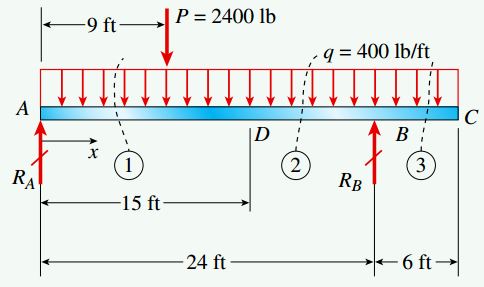
بر اساس نمودار جسم آزاد کل تیر (شکل بالا) میتوانیم نیروهای عکسالعمل RA و RB را به ترتیب با جمع نیروهای موجود در راستای y و جمع گشتاورهای حول نقطه A به دست بیاوریم:
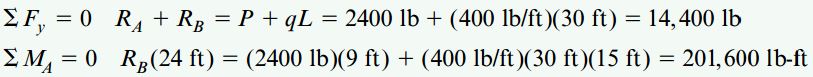
با حل معادله دوم، RB=8400lb و با قرار دادن این مقدار در معادله اول و حل آن، RA=6000lb خواهد بود. این مقادیر برای تعیین توابع (V(x و (M(x در برشهای مختلف مورد استفاده قرار میگیرند.
نیروی برشی (V(x و گشتاور خمشی (M(x
بر اساس مکانهای مشخص شده در شکل قبلی (شمارههای 1 تا 3)، نمودار جسم آزاد کل تیر را به سه نمودار جسم آزاد مجزا تقسیم میکنیم. توجه داشته باشید که دو نمودار، برش مربوطه نسبت به تکیهگاه سمت چپ و در یک نمودار، این برش نسبت تکیهگاه سمت راست ایجاد شده است.

اکنون از نمودارهای جسم آزاد بالا برای تعیین توابع (V(x در بخشهای مختلف تیر استفاده میکنیم:
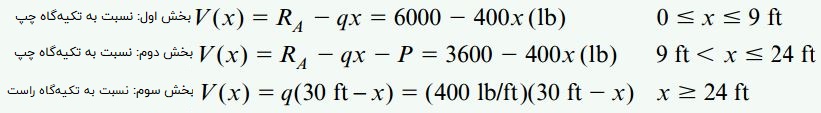
برای نمودار جسم آزاد سوم بخش سوم (نمودار راست)، یافتن تابع (V(x با استفاده از بخش سمت راست تیر راحتتر از به کارگیری بخش سمت چپ است (به دلیل عدم وجود نیروی عکسالعمل RA و بار P در نمودار سمت راست). در مرحله بعد، توابع (M(x در هر یک از بخشها را به دست میآوریم:
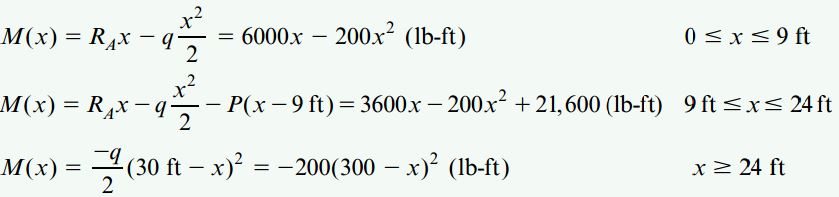
مقدار ماکسیمم نیروی برشی در فاصله بین تکیهگاههای A و B رخ میدهد. گشتاور خمشی ماکسیمم نیز در محلی با V=0 اعمال میشود. اگر تابع (V(x را برابر با صفر قرار دهیم، محل رخ دادن گشتاور خمشی ماکسیمم در x=xm=9ft به دست میآید. با جایگذاری xm در تابع گشتاور، مقدار M(xm)=Mmax=37800lb-ft نیز تعیین میشود.
نمودارهای نیروی برشی و گشتاور خمشی
یکی از روشهای رسم نمودارهای نیروی برشی و گشتاور خمشی، تعیین توابع (V(x و (M(x برای تمام طول تیر و استفاده از نرمافزارهای کامپیوتری به منظور رسم این نمودارها است. در روش دیگر، از تفسیر گرافیکی روابط بین بار، نیروی برشی و گشتاور خمشی برای رسم نمودارهای V و M استفاده میشود. بر اساس این روش گرافیکی، نمودارهای زیر به دست میآیند:
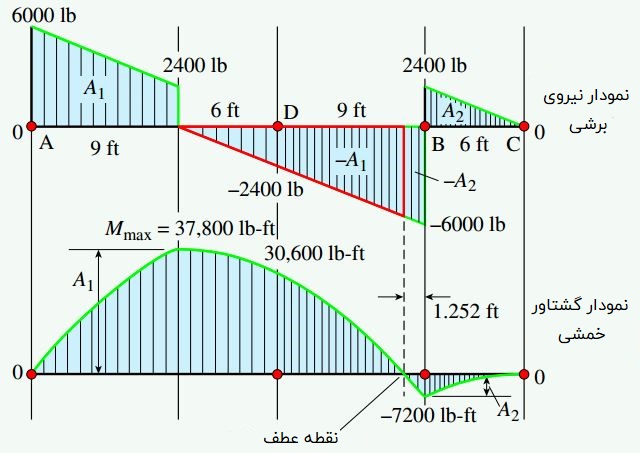
در ادامه، نکات مورد نیاز برای مراحل رسم نمودارهای بالا را به صورت گام به گام توضیح میدهیم:
- الف: مقدار نیروی برشی V در فاصله بسیار کمی از سمت راستِ نقطه A با نیروی عکسالعمل RA برابر است. با فاصله گرفتن از این نقطه، نیروی برشی متناسب با شدت بار q بر واحد فوت کاهش مییابد. به این ترتیب، در فاصله x=9ft، مقدار این نیرو از 6000lb به [6000lb-(9ft*400lb/ft)=2400lb] میرسد.
- ب: شیب خط مماس بر نمودار نیروی برشی با مقدار منفی عرض نمودار بارگذاری برابر است (dV/dx=-q(x. به دلیل ثابت بودن بار (q(x، نیروی برشی به صورت خطی تغییر میکند.
- ج: در فاصله بسیار کوچکی از سمت راست محل اعمال بار متمرکز، مقدار نیروی برشی (2400lb) به اندازه P=2400lb کاهش مییابد. به این ترتیب، نیروی برشی در این نقطه به مقدار صفر میرسد. در نتیجه، این نقطه (xm=9ft) بیانگر محل رخ دادن گشتاور ماکسیمم مثبت خواهد بود.
- د: میزان تغییرات گشتاور خمشی از تکیهگاه A (فاصله x=0) تا محل رخ دادن گشتاور ماکسیمم (x=9ft) با مساحت زیر نمودار نیروی برشی در همین محدوده برابر خواهد بود. این ناحیه ذوزنقهای شکل در نمودار نیروی برشی با عنوان A1 علامتگذاری شده است:

- ه: رابطه انتگرالی بین بار و نیروی برشی نشان میدهند که به دلیل ثابت بودن نمودار بارگذاری (q(x، نمودار نیروی برشی (V(x خطی خواهد بود. علاوه بر این، رابطه انتگرالی بین نیروی برشی و گشتاور خمشی نیز بیان میکند که به دلیل خطی بودن نمودار نیروی برشی (V(x، نمودار گشتاور خمشی (M(x به صورت یک منحنی درجه دو خواهد بود.
- و: مقدار نیروی برشی در نقطه D با 6ft)*(q)=-2400lb-) برابر است (علامت منفی، رو به پایین بودن جهت اعمال نیرو را نمایش میدهد). به این ترتیب، نیروی برشی در x=D نسبت به x=xm مقدار کمتری دارد. مقدار گشتاور خمشی در نقطه D از اختلاف بین Mmax با مساحت مثلث تشکیل شده در نمودار نیروی برشی (بین فاصله x=xm تا x=15ft) به دست میآید:
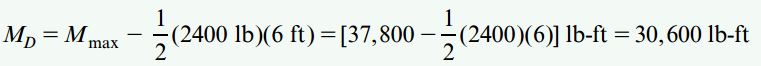
- ز: با جایگذاری مساحت کل مثلث تشکیل شده در نمودار نیروی برشی (بین فاصله x=xm تا x=24ft)، گشتاور خمشی اعمال شده در نقطه B به صورت زیر تعیین میشود:

- ق: با عبور از نقطه B بر روی نمودار نیروی برشی و در فاصله بسیار کوچکی از سمت راست این نقطه، مقدار نیروی برشی از 6000lb- تا 2400lb+ تغییر افزایش مییابد. این افزایش 8400 پوندی نیروی برشی به دلیل وجود نیروی عکسالعمل RB در تکیهگاه B رخ میدهد.
- ر: مقدار گشتاور خمشی در نزدیکی سمت چپ نقطه B برابر با صفر است. این محل با عنوان «نقطه عطف» (Inflection Point) شناخته میشود. اگر دو ناحیه علامتگذاری شده با A1 در نمودار نیروی برشی را با هم برابر قرار دهیم، فاصله بین نقطه عطف تا تکیهگاه B به دست میآید. ناحیه زیر نمودار نیروی برشی در فاصله بین B تا C که با A2 علامتگذاری شده برابر با 7200lb-ft است. با افزودن این عدد به گشتاور MB، نمودار گشتاور خمشی در نقطه C به مقدار صفر بازمیگردد.

در شکل بالا، از روش تفسیر گرافیکی روابط تفاضلی و انتگرالی بین بار، نیروی برشی و گشتاور خمشی برای رسم نمودارهای نیروی برشی و گشتاور خمشی استفاده شد. توابع (V(x و (M(x را میتوان با استفاده از نرمافزارهای پرکاربردی نظیر Maple، MATLAB و .. نیز قابل رسم هستند.
توجه داشته باشید که نمودار گشتاور خمشی بر اساس سطح تحت فشار تیر رسم میشود. از اینرو، بخش زیادی از سطح بالایی تیر (از نقطه A تا نقطه عطف) در معرض فشار و بخش دیگر آن (از نقطه عطف تا نقطه C) در معرض کشش قرار دارد. این مسئله در طراحی تیرهای ساخته شده از مواد خاص دارای اهمیت بالایی است.
مثال 4
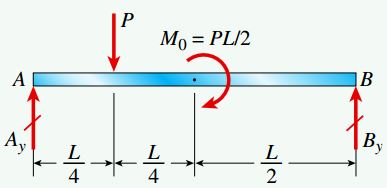
شکل زیر، تیر سادهای را نمایش میدهد که در معرض یک نیروی متمرکز (P) و یک کوپل (M0) قرار گرفته است. با فرض M0=PL/2، نمودارهای نیروی برشی و گشتاور خمشی این تیر را رسم کنید.
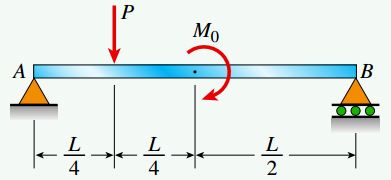
در مرحله اول تحلیل مسئله، نمودار جسم آزاد کل تیر را مطابق شکل زیر رسم میکنیم و با استفاده از آن، نیروهای عکسالعمل Ay و By را به دست میآوریم.
با جمع گشتاورهای حول نقطه B خواهیم داشت:
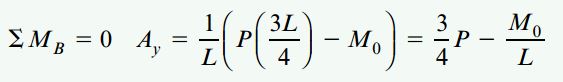
با جمع نیروهای موجود در راستای عمودی نیز داریم:

اگر M0=PL/2 را در معادلات بالا جایگزین کنیم، Ay=P/4 و By=3P/4 خواهد بود. به منظور مشخص کردن نیروی برشی V و گشتاور خمشی M در بخشهای مختلف تیر، سه برش را در نمودار جسم آزاد کل ایجاد میکنیم. به این ترتیب، سه نمودار جسم آزاد مجزا مطابق شکل زیر به دست میآید.
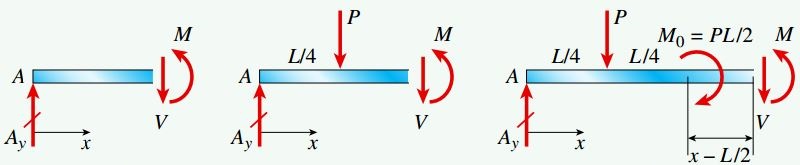
نیروی برشی (V(x و گشتاور خمشی (M(x
در این مرحله، نمودارهای جسم آزاد هر بخش را برای تعیین توابع نیروی برشی و گشتاور خمشی مورد استفاده قرار میدهیم:
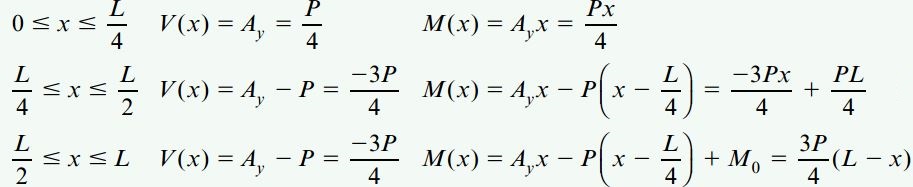
توجه داشته باشید که اگر برای بخش سوم (نمودار راست) از بخش سمت راست تیر استفاده میکردیم، روابط مربوط به تعیین V و M برای این محدوده راحتتر به دست میآمدند.
نمودارهای نیروی برشی و گشتاور خمشی
به منظور رسم نمودارهای مربوطه از روش تفسیر گرافیکی روابط تفاضلی و انتگرالی میان بار، نیروی برشی و گشتاور خمشی استفاده میکنیم. نمودارهای نیروی برشی و گشتاور خمشی این مسئله به صورت زیر هستند.
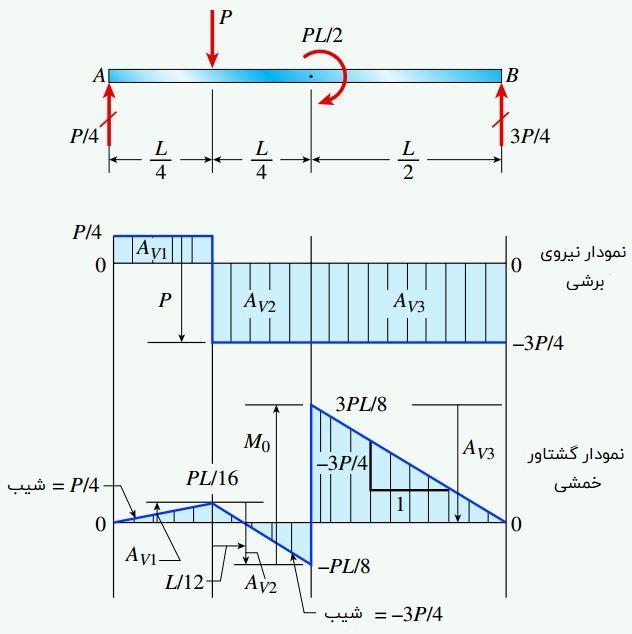
نمودارهای بالا با به کارگیری مراحل زیر به دست آمدهاند:
- به دلیل عدم اعمال بار گسترده (q(x بر روی تیر، نمودار نیروی برشی از چند خط مستقیم با شیب صفر ایجاد میشود (dV/dx=q=0). توجه داشته باشید که مشتق dV/dx در هر سه بخش تیر برابر با صفر است.
- در محل اعمال بار متمرکز (فاصله x=L/4)، نمودار به طور ناگهانی و به اندازه P کاهش مییابد.
- در محل اعمال کوپل (فاصله x=L/2)، نمودار گشتاور خمشی به اندازه M0=PL/2 افزایش مییابد.
در بخش اول، شیب نمودار گشتاور خمشی برابر +P/4 است (ارتفاع نمودار نیروی برشی در این محدوده). در بخشهای دوم و سوم، شیب نمودار گشتاور خمشی با مقدار 3P/4- برابری میکند. رسم این نمودار از رابطه تفاضلی dM/dx=V پیروی میکند. به این ترتیب، شیب هر بخش تیر از مشتق تابع (M(x به دست میآید.
نواحی نامگذاری شده با AV بر روی نمودار نیروی برشی، میزان تغییر ارتفاع هر بخش بر روی نمودار گشتاور خمشی را نمایش میدهند. به عنوان مثال، گشتاور خمشی از مقدار صفر در نقطه A به مقدار AVI=PL/16 در نقطه x=L/4 تغییر میکند.

با توجه به نمودار گشتاور خمشی، بیشتر سطح بالایی تر در معرض فشار قرار گرفته است. در فاصله x=L/12 از محل اعمال بار متمرکز (در فاصله x=L/4+L/12=L/3) نیز یک نقطه عطف وجود دارد. این نقطه با جایگذاری x=L/3 در معادله گشتاور خمشی بخش دوم تیر نیز به دست میآید (M(L/3)=0).
مثال 5
شکل زیر سه تیر را نمایش میدهد که در معرض یک بار گسترده متغیر با شدت q(x)=xq0/L قرار گرفتهاند. نحوه نگهداری هر یک از این تیرها با هم تفاوت دارد. با استفاده از روش تفسیر گرافیکی روابط تفاضلی و انتگرالی بین بار، نیروی برشی و گشتاور خمشی، نمودارهای نیروی برشی و گشتاور خمشی هر یک را رسم کنید.
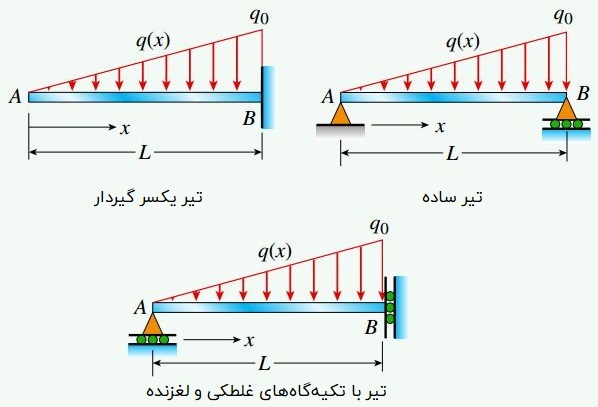
در مرحله اول، با رسم نمودارهای جسم آزاد کل هر تیر، نیروهای عکسالعمل RA و RB را تعیین میکنیم. نیروی برشی V و گشتاور خمشی M نیز از جمع نیروهای هم راستا و جمع گشتاورهای حول مقطعی در فاصله x از تکیهگاه A به دست میآیند.
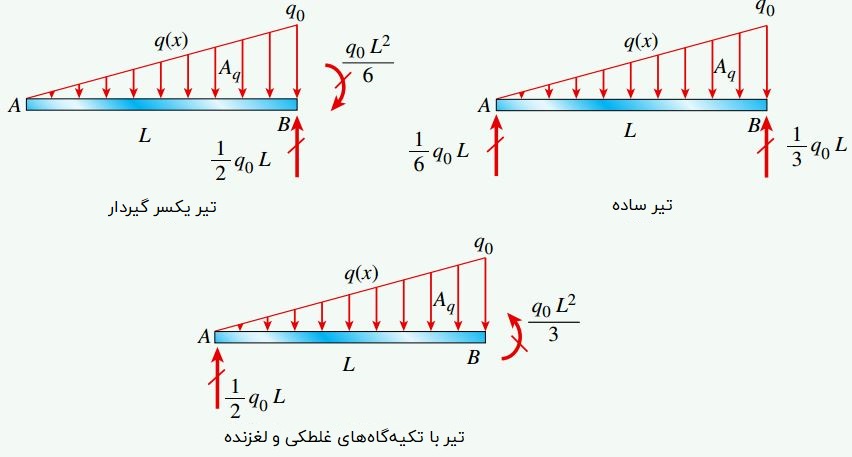
مثالهای قبلی را با به دست آوردن توابع (V(x و (M(x مورد تحلیل قرار دادیم. این مثال را نیز میتوان به همان روش حل کرد. با این وجود، در این مسئله از یک رویکرد کارآمدتر برای تعیین رابطه تفاضلی و انتگرالی بین بار، نیروی برشی و گشتاور خمشی به منظور رسم نمودارهای V و M استفاده خواهیم کرد.
تیر یکسر گیردار
اگر یک بار گسترده بر روی تمام طول تیر اعمال شود، رابطه بین مقادیر نیروهای برشی و شدت بار در فاصله میان دو نقطه مورد بررسی به صورت زیر خواهد بود:

برای تیر یکسر گیردار مورد تحلیل در این مثال، نیروی برشی V در فاصله x از انتهای A با استفاده از انتگرال زیر به دست میآید:
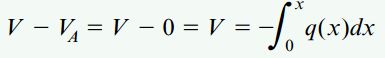
با انتگرالگیری بر روی کل تیر میتوان دریافت که تغییرات نیروی برشی در محدوده A تا B با مقدار منفی مساحت زیر نمودار بار گسترده (Aq-) در شکل زیر برابر است.
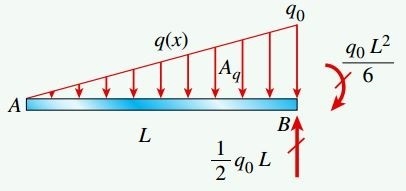
شیب خط مماس بر نمودار نیروی برشی در هر نقطهای با ارتفاع نمودار بار گسترده در همان نقطه برابر است. به دلیل تغییرات خطی نمودار بارگذاری، نمودار نیروی برشی با مرتبه دو تغییر میکند (رابطه انتگرالی بین بار و نیروی برشی).

در صورت اعمال یک بار گسترده بر روی تمام طول تیر، رابطه بین مقادیر نیروهای برشی و گشتاورهای خمشی در فاصله میان دو نقطه مورد بررسی به صورت زیر خواهد بود:

به این ترتیب، گشتاور خمشی M در فاصله x از نقطه A با انتگرالگیری از تابع نیروی برشی در محدوده مورد نظر به دست میآید:

با انتگرالگیری از تمام طول تیر میتوان مشاهده کرد که تغییرات گشتاور خمشی در فاصله بین نقاط A و B با مقدار مساحت زیر نمودار نیروی برشی (AV) برابر است. علاوه بر این، شیب خط مماس بر نمودار گشتاور خمشی در هر نقطه، ارتفاع نمودار نیروی برشی در همان نقطه را نمایش میدهد. به دلیل تغییرات درجه دو نمودار نیروی برشی، نمودار گشتاور خمشی با مرتبه سه تغییر میکند (رابطه انتگرالی بین این دو کمیت). مقادیر ماکسیمم نیروی برشی و گشتاور خمشی در محل قرارگیری تکیهگاه ثابت (x=L) رخ میدهد.

تیر ساده
در تیر ساده نیز همانند تحلیل تیر یکسر گیردار، شیب نمودار نیروی برشی در هر نقطه با مقدار منفی (q(x و شیب نمودار گشتاور خمشی با (V(x در آن نقطه برابر خواهد بود. نیروی برشی ماکسیمم در محل تکیهگاه B (فاصله x=L از تکیهگاه A) و گشتاور خمشی ماکسیمم نیز در نقطه V=0 (فاصله xm=L/(3)0.5) رخ میدهد. با جایگذاری xm در تابع (M(x، مقدار گشتاور خمشی ماکسیمم به دست میآید. به طور کلی برای تیر ساده، میزان تغییرات نیروی برشی در فاصله میان A تا B با مقدار منفی مساحت زیر نمودار بارگذاری Aq-) و میزان تغییرات گشتاور خمشی در این محدوده با مساحت زیر نمودار نیروی برشی (AV) برابری میکند.
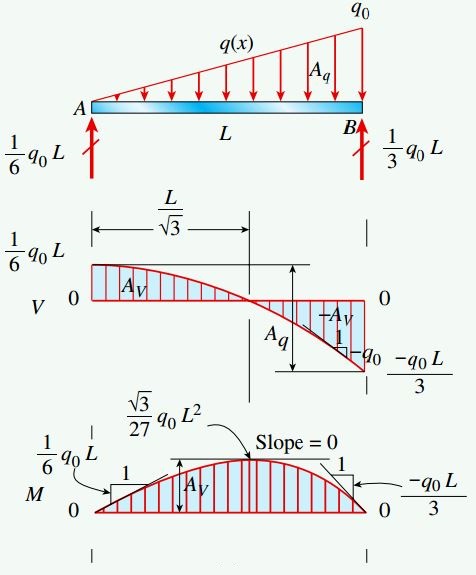
تیر با تکیهگاههای غلتکی و لغزنده
در تیر سوم، کل بار گسترده (Aq=q0L/2) بر روی تکیهگاه A اعمال میشود. به همین دلیل، نیروی برشی ماکسیمم در این محل رخ میدهد. با دور شدن از نقطه A، میزان نیروی برشی با پیروی از یک منحنی مرتبه دو از مقدار Aq در تکیهگاه A تا مقدار صفر در تکیهگاه لغزنده B کاهش مییابد (تکیهگاههای لغزنده قابلیت مقاومت در برابر نیروهای عمودی را ندارند). به دلیل صفر بودن نیروی برشی در تکیهگاه B، گشتاور خمشی ماکسیمم نیز در این محل رخ خواهد داد. مقدار این گشتاور با مساحت زیر کل نمودار نیروی برشی AV=q0L2/3 برابر است.
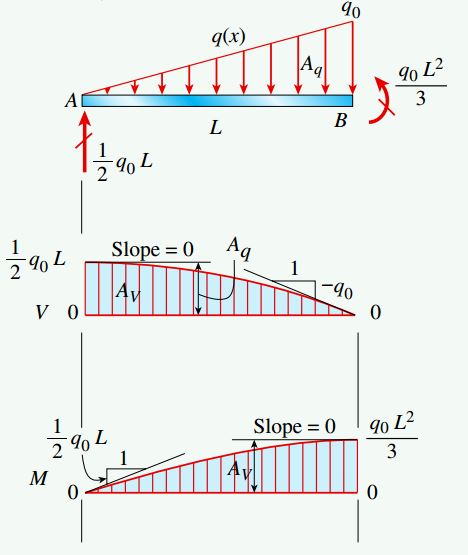
در این مثال، به دلیل الگوی خطی و پیوسته بودن بارگذاری و همچنین عدم اعمال بارهای متمرکز یا کوپلها بر روی تیر، انتگرال گرفتن از محدودههای مورد بررسی کار سادهای خواهد بود. با این وجود، اگر بار متمرکز یا کوپل بر روی تیر اعمال میشد، چند ناپیوستگی در نمودار نیروی برشی و گشتاور خمشی هر تیر به وجود میآمد. توجه داشته باشید که در این حالت باید از روابط جداگانهای برای هر بخش تیر استفاده کنیم. در دو مثال بعدی، شرایط پیچیدهتری را به صورت عددی مورد تحلیل قرار خواهیم داد.
مثال 6
شکل زیر، قابی را نمایش میدهد که در معرض سطح آن در معرض بارهای متمرکز و گسترده (یکنواخت و متغیر) قرار گرفته است. گشتاور MA نیز در نقطه A بر روی تکیهگاه لولایی و نیروی مورب FB بر روی مفصل B اعمال میشود. بار گسترده یکنواختی با شدت q1 بر روی سطح عضو BC (رو به راست) و بار گسترده متغیری با شدت حداکثری q0 بر روی عضو ED (رو به پایین) عمل میکند. مقدار عددی هر یک از کمیتها در شکل زیر نمایش داده شده است. با توجه به اطلاعات مسئله:
- الف: عکسالعملهای تکیهگاهی موجود در نقاط A و C را پیدا کنید.
- ب: نیروهای داخلی موجود بر روی عضو BC را به دست آورید.
- ج: نمودارهای نیروی محوری، نیروی برشی و گشتاور خمشی تمام عضوهای قاب را رسم کنید.

نمودارهای جسم آزاد
در صورت رسم نمودار جسم آزاد کل سازه مطابق شکل زیر، نیروهای عکسالعمل موجود در تکیهگاههای A و D قابل محاسبه خواهند بود. بارهای گسترده اعمال شده بر روی عضوهای ED و BC را میتوانیم به ترتیب با استفاده از نیروهای برآیند Fq0 و Fq1 نمایش دهیم. هر یک از این نیروهای برآیند از مرکز هندسی بار گسترده مرتبط با خود عبور میکنند. به علاوه، مقدار آنها با مساحت زیر نمودار بارگذاری (مثلث و مستطیل) برابر است.
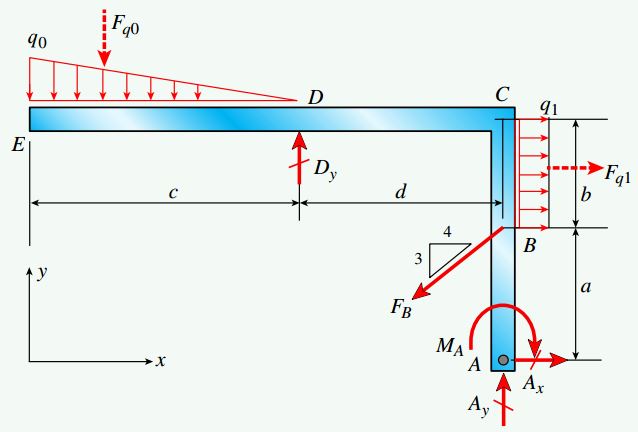
اگر پایینتر از محل قرارگیری مفصل C یک برش را در نمودار جسم آزاد بالا ایجاد کنیم، امکان تعیین نیروی محوری NC، نیروی برشی VC و گشتاور خمشی MC در نزدیکی نقطه C فراهم میشود. نمودارهای ایجاد شده توسط این برش را میتوان به منظور تعیین نیروها و گشتاورهای داخلی موجود در محل برش مورد استفاده قرار داد.
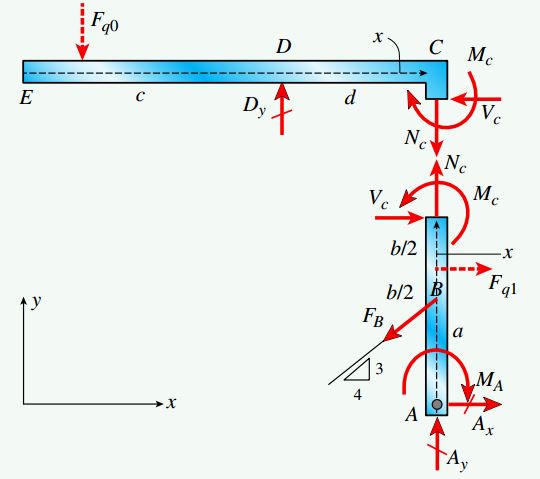
فرآیند حل مسئله
قاب مورد تحلیل در این مسئله از نظر استاتیکی معین است. در ابتدا با به کارگیری نمودار جسم آزاد کل سازه، نیروهای عکسالعمل موجود در نقاط A و D را محاسبه میکنیم. سپس، یکی از نمودارهای جسم آزاد بخش بالایی یا پایینی قاب را به منظور تعیین نیروها و گشتاورهای داخلی موجود در زیر مفصل C مورد استفاده قرار میدهیم. در مرحله بعد، هر یک از عضوهای ABC و EDC را به عنوان تیرهای جداگانه با مرکز هندسی مجزا (در راستای محور x) در نظر میگیریم. پس از این مرحله، توابع نیروی محوری (N(x، نیروی برشی (V(x و گشتاور خمشی (M(x را به دست میآوریم. در انتها نیز با کمک این توابع، نمودارهای مرتبط با هر عضو را رسم میکنیم.
مؤلفههای نیروی متمرکز و برآیندهای بارهای گسترده
به منظور تعیین مقادیر مؤلفههای نیرو، به جای بارهای گسترده از برآیند آنها (Fq0 و Fq1) استفاده میکنیم. بار Fq0 در فاصله c/3=6ft از نقطه E به صورت رو به پایین و بار Fq1 در مرکز BC به صورت رو به راست اعمال میشود. به دلیل مورب بودن نیروی متمرکز FB، باید مؤلفههای عمودی و افقی آن را به دست بیاوریم. مقادیر برآیندهای بارهای گسترده و مؤلفههای نیروی FB به صورت زیر مورد محاسبه قرار میگیرند:
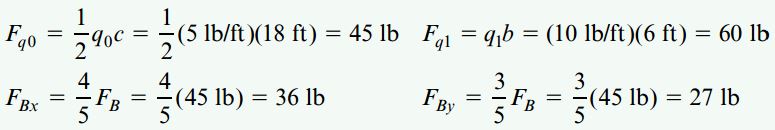
عکسالعملهای خارجی
با استفاده از قاعده علامتگذاری استاتیک، گشتاورها و نیروهای عکسالعمل در راستاهای مختلف را به دست میآوریم:
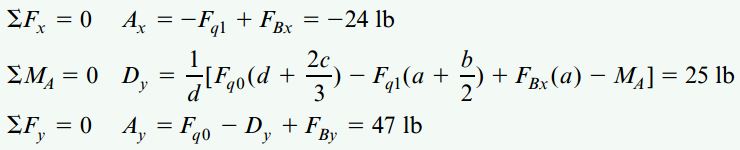
نیروهای داخلی N و V و گشتاور M در پایین نقطه C
با استفاده از قواعد علامتگذاری تغییر شکل، کمیتهای داخلی VC ،NC و MC را تعیین میکنیم. بر اساس این قواعد، جهت اعمال کمیتهای داخلی مذکور مثبت در شکل زیر مثبت است.

اگر تعادل نمودار جسم آزاد بالایی را در نظر بگیریم، خواهیم داشت:
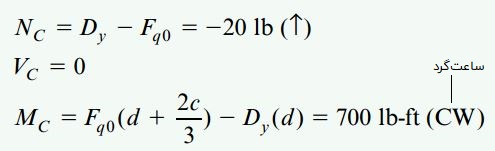
با توجه به منفی بودن NC، جهت فرضی ما در نمودار جسم آزاد بالایی درست نیست. به همین دلیل، در کنار مقدار به دست آمده برای این کمیت از یک پیکان رو به بالا استفاده میکنیم. بر اساس نتایج بالا، جهت فرضی گشتاور MC (چرخش ساعتگرد) با جهت واقعی آن مطابقت دارد.
توابع نیروی محوری، نیروی برشی و گشتاور خمشی
برای به دست آوردن توابع نیروی محوری، نیروی برشی و گشتاور خمشی، هر عضو را به عنوان یک تیر مجزا در نظر میگیریم.
تیر EDC (نمودار جسم آزاد بخش بالایی)
برای تحلیل این تیر، بار مثلثی اعمال شده بر روی محدوده ED را مطابق شکل زیر به بخشهای مثلثی تقسیم میکنیم:
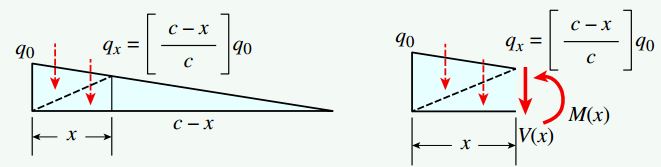
مقدار تابع (N(X بر روی تمام طول تیر برابر با صفر است. به همین دلیل، رابطه مربوط به این تابع را فقط برای یک محدوده (0 تا c+d) مینویسیم. با این وجود، باید روابط مربوط به توابع (V(x و (M(x را برای دو بخش تیر EDC تعیین کنیم:
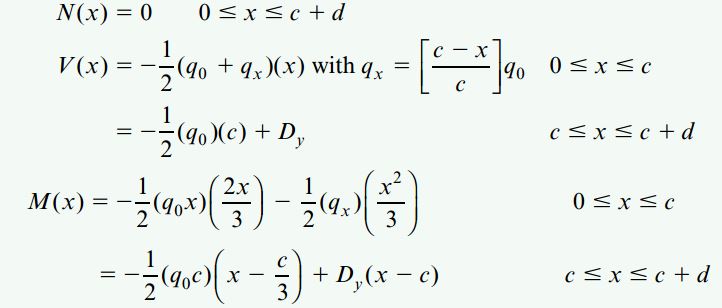
توجه داشته باشید که رابطه qx با استفاده از تشابه مثلثها به دست آمده است.
تیر ABC (نمودار جسم آزاد بخش پایینی)
به منظور تعیین توابع نیروی محوری، نیروی برشی و گشتاور خمشی برای دو بخش AB و BC، ستون ABC را به عنوان یک تیر مجزا در نظر میگیریم. مبدأ این تیر در نقطه A قرار دارد. برای درک بهتر این موضوع میتوانیم تیر ABC را به صورت ساعتگرد و به اندازه 90 درجه دوران دهیم تا بر روی محور افقی قرار گیرد.

به این ترتیب، توابع (V(x) ،N(x و (M(x به صورت زیر خواهند بود:

توجه داشته باشید که روابط V(a+b)=VC ،N(a+b)=NC و M(a+b)=MC بین توابع بالا و نیروهای داخلی در نقطه C برقرار است. از این نکته میتوان برای تأیید صحت روابط به دست آمده در این بخش استفاده کرد.
نمودارهای نیروی محوری، نیروی برشی و گشتاور خمشی
شکلهای زیر، نمودارهای نیروی محوری، نیروی برشی و گشتاور خمشی قاب مورد تحلیل را نمایش میدهند. این نمودارها با استفاده از توابع (V(x) ،N(x و (M(x در بخشهای مختلف قاب رسم شدهاند.

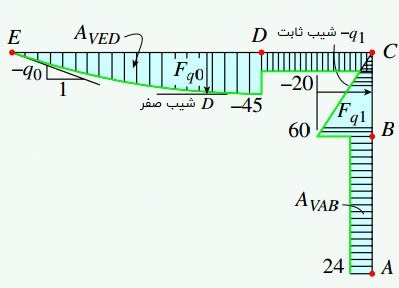
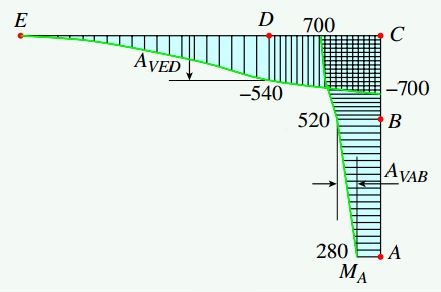
با بررسی نمودارهای بالا میتوان به نتایج زیر رسید:
- نیروی محوری در هر بخشهای AB و BC به صورت فشاری و دارای مقداری ثابت است. مقدار این نیرو در بخش AB با Ay- و در بخش BC با NC برابری میکند.
- به دلیل رو به پایین بودن بار گسترده q0، شیب خط مماس بر نمودار نیروی برشی (dV/dx) در نقطه E با مقدار منفی q0 برابر است ((dV/dx=-d(x). در نقطه D، ارتفاع q به مقدار صفر میرسد. از اینرو، شیب نمودار نیروی برشی بر روی این نقطه نیز صفر میشود. از آنجایی که مساحت زیر منحنی بارگذاری در فاصله بین نقاط E تا D برابر با Fq0 است، تغییرات نیروی برشی در این محدوده برابر با Fq0- خواهد بود. تغییرات نیروی برشی در نقطه D به Dy=25lb+ میرسد و تا نقطه C ثابت باقی میماند. مقدار این نیرو در نزدیکی مفصل C با NC برابر است.
- مساحت زیر نمودار نیروی برشی از نقطه E تا D با AVED نمایش داده میشود. مقدار این مساحت با میزان تغییرات گشتاور خمشی در محدوده مذکور برابر است. تغییرات گشتاور خمشی از نقطه D تا C نیز با مقدار منفی مساحت مستطیل تشکیل شده در زیر نمودار نیروی برشی برابری میکند (20lb*d=-160lb-ft-).
- به دلیل عدم اعمال بار گسترده از نقطه A تا B، مقدار نیروی برشی در این محدوده ثابت است. وجود بار متمرکز FB در نقطه B، باعث افزایش نیروی برشی به اندازه مؤلفه FBx=36lb میشود. پس از نقطه B، این نیرو به صورت خطی و با شیب q- کاهش مییابد و در مفصل C، به مقدار VC=0 میرسد. میزان تغییرات نیروی برشی در محدوده B تا C با Fq1- (مساحت زیر نمودار بارگذاری) برابر است.
- میزان تغییرات گشتاور خمشی از تکیهگاه A (محل اعمال گشتاور MA) تا نقطه B با مقدار مثبت مساحت زیر نمودار نیروی برشی در همین محدوده برابر است (AVAB=24lb*10ft=240lb-ft). گشتاور خمشی از نقطه B تا C به اندازه مساحت زیر نمودار نیروی برشی در همین فاصله (60lb*b/2=180lb-ft) افزایش مییابد.
- با توجه به نمودارهای به دست آمده، مقدار ماکسیمم نیروی محوری فشاری بر روی بخش AB؛ نیروی برشی ماکسیمم بر روی عضو AB و در بالای مفصل B؛ و گشتاور خمشی ماکسیمم نیز بر روی هر دو سمت مفصل C رخ میدهد.



- نمودارهای نیروی محوری، نیروی برشی و گشتاور خمشی قابها معمولاً مانند موارد بالا بر روی قاب رسم میشوند. هیچ نیروی محوری به تیر EDC اعمال نمیشود اما تمام ارتفاع ستون ABC تحت فشار قرار دارد. نمودار گشتاور خمشی نشان میدهد که بخش سمت چپ ستون AB و بخش زیرین تیر EDC در معرض فشار قرار گرفته است.
- اتصال بین تیر EDC و ستون ABC، یکی از ویژگیهای مهم در طراحی این قاب است. به منظور تعیین نیروها و گشتاورهای اعمال شده بر روی این اتصال باید از نمودارهای V ،N و M و نمودار جسم آزاد اتصال C استفاده کنیم (شکل زیر).

با توجه به نمودار جسم آزاد بالا میتوان مشاهده که تعادل نیرو و گشتاور در اتصال C برقرار است. نیروی برشی بخش سمت چپ این اتصال (نیروی VCD) با نیروی محوری در بخش BC (نیروی NBC) برابری میکند. در حالی که نیروی برشی بخش پایینی اتصال C (نیروی VBC) با نیروی محوری انتهای عضو DC (نیروی NCD) یکسان است.
مثال 7
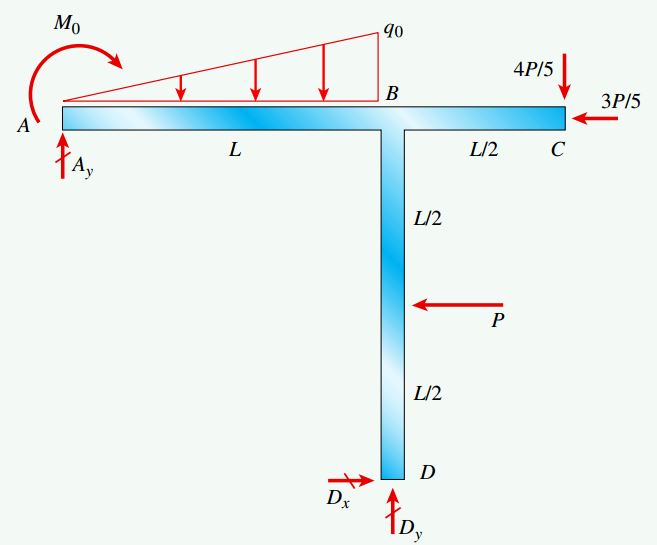
شکل زیر، قابی با یک تکیهگاه غلتکی در نقطه A و یک تکیهگاه گیردار در نقطه D را نمایش میدهد. بار گسترده متغیر با شدت حداکثری q0=10lb/ft بر روی محدوده AB و گشتاور متمرکز M0=300lb-ft بر روی تکیهگاه A اعمال میشود.
علاوه بر این، انتهای بخش آزاد قاب در نقطه C تحت بار متمرکز مورب P=40lb و مرکز ستون BD نیز تحت بار متمرکز افقی P=40lb قرار دارد. طول بخشهای AB و BD برابر با L=12ft و طول بخش آزاد BC برابر با 6ft است. با توجه به اطلاعات مسئله، نمودارهای نیروی محوری، نیروی برشی و گشتاور خمشی این قاب را رسم کنید.

برای شروع حل این مسئله، ابتدا نمودار جسم آزاد کل قاب را مطابق شکل زیر رسم میکنیم. سپس، نیروهای عکسالعمل Dx ،Ay و Dy را به دست میآوریم. به منظور نمایش نیروی محوری N، نیروی برشی V و گشتاور خمشی M در هر بخش، قاب را در مقاطع مناسب برش میدهیم.
بر اساس قواعد علامتگذاری تغییر شکل، جهت اعمال نیروی محوری، نیروی برشی و گشتاور خمشی موجود در نمودارهای جسم آزاد زیر مثبت در نظر گرفته میشود. هر برش، سازه را به دو بخش مجزا تقسیم میکند. با انتخاب هر یک از این بخشها میتوان مقادیر V ،N و M را در محل مورد نظر به دست آورد.
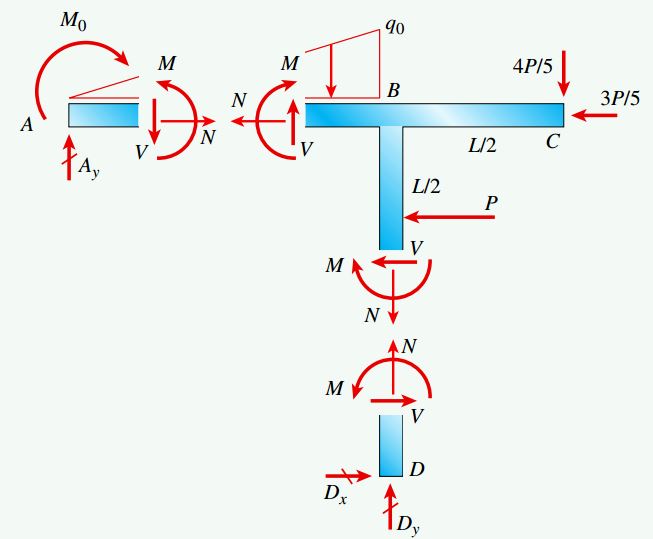
عکسالعملهای خارجی
اگر نیروهای موجود در راستای x و گشتاورهای حول نقطه D را با هم جمع کنیم، مقادیر نیروی عکسالعمل Dx و Ay تعیین میشوند. با جمع نیروهای موجود در راستای y نیز، نیروی عکسالعمل Dy به دست میآید:
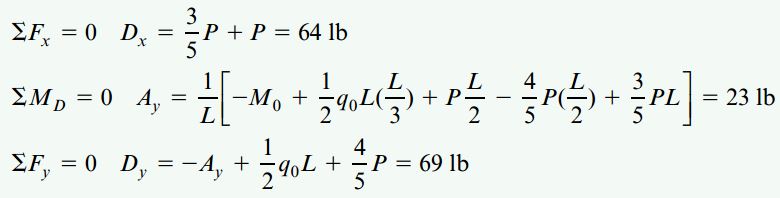
توجه: به منظور تعیین نیروهای عکسالعمل تکیهگاهی از قواعد علامتگذاری استاتیک استفاده میکنیم.
با توجه به مثبت بودن علامت نتایج به دست آمده، جهت فرضی اعمال آنها در نمودار جسم آزاد صحیح خواهد بود. برآیند نیروهای عکسالعمل در نقطه D به صورت زیر تعیین میشود:

تمام مؤلفههای نیروی عکسالعمل در شکل زیر نمایش داده شدهاند.

نیروی محوری N، نیروی برشی V و گشتاور خمشی M
به منظور رسم نمودارهای نیروی محوری، نیروی برشی و گشتاور خمشی دو روش وجود دارد. در گزینه اول، نمودار بالا به منظور تعیین توابع (N(x) ،V(x و (M(x و رسم نمودارهای N ،V و M به کار گرفته میشود. در گزینه دوم، روابط تفاضلی و هندسی بین بار، نیروی برشی و گشتاور خمشی مورد استفاده قرار میگیرند.
عضو AB
با استفاده از نمودار جسم آزاد سمت چپ، داریم:
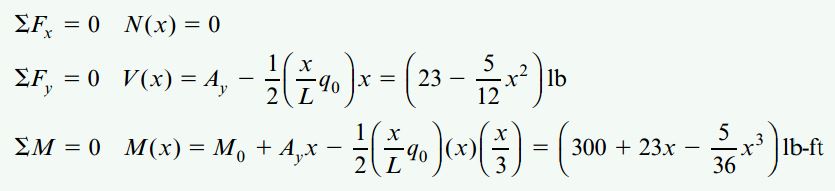
شکل زیر، نمودار نیروی برشی (V(x را نمایش میدهد. نیروی برشی در نزدیکی نقطه A با Ay=23lb برابر است. با حرکت به سمت نقطه B، این نیرو به اندازه 60lb (مساحت زیر نمودار بارگذاری در محدوده A تا B) افزایش مییابد.
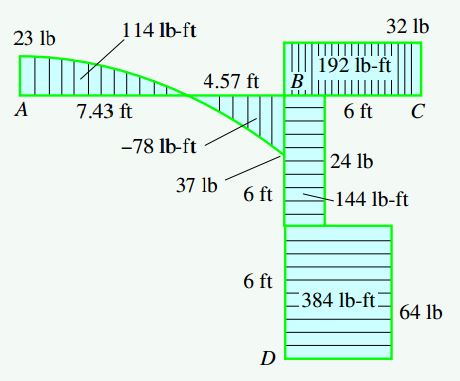
شکل زیر، نمودار گشتاور خمشی (M(x را نمایش میدهد. مقدار گشتاور خمشی در نقطه A با M0=300lb-ft برابر است. با حرکت به سمت راست، این گشتاور تا فاصله x=7.43ft (محل رخ دادن نیروی برشی صفر) به اندازه 114lb-ft (مساحت زیر نمودار نیروی برشی در محدوده A تا x=7.43ft) افزایش مییابد و به مقدار حداکثری 414lbft- میرسد. سپس، در محدوده x=7.43ft تا مفصل B به اندازه 78lb-ft کاهش مییابد.
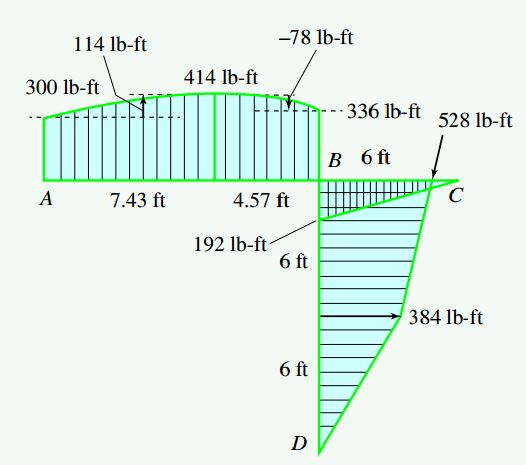
عضو BC
اگر عضو BC را در نزدیکی سمت راست B برش دهیم، کمیتهای V ،N و M در تیر BC قابل محاسبه خواهند بود. در این تیر، نقطه B را به عنوان مبنای فاصله x در نظر میگیریم و از نمودار جسم آزاد سمت راست آن برای تعیین توابع (N(x) ،V(x و (M(x استفاده میکنیم:

نیروی محوری N بر روی عضو BC به صورت فشاری و دارای مقداری ثابت است. با توجه به توابع در رسم شده در نمودارهای زیر مشاهده میشود که نیروی برشی در محدوده BC تغییر نمیکند. مساحت زیر نمودار نیروی برشی در این محدوده با مقدار 32lb*6ft=+192lb-ft+ برابری میکند. این عدد، میزان تغییرات گشتاور خمشی در فاصله B تا C را نمایش میدهد.
عضو DB
در مرحله آخر، عضو DB را در دو محل (بالا و پایین محل اعمال بار متمرکز P) برش میدهیم. سپس با در نظر گرفتن نقطه D به عنوان مبنای فاصله x، توابع (N(x) ،V(x و (M(x را به صورت زیر مینویسیم:
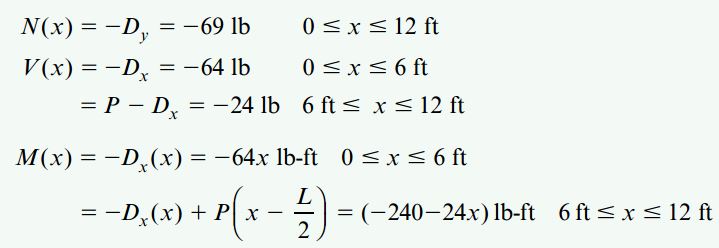
نیروی محوری N بر روی عضو DB نیز همانند عضو BC به صورت فشاری و دارای مقداری ثابت است. نیروی برشی و گشتاور خمشی در محدوده DB منفی هستند (با در نظر گرفتن نقطه D به عنوان مبنا، سمت راست ستون به عنوان بخش منفی محسوب خواهد شد). توجه داشته باشید که مساحت زیر نمودار نیروی برشی در نیمه اول DB، برابر با 64lb*6ft=-384lb-ft- است و میزان تغییرات گشتاور خمشی در این محدوده را نمایش میدهد. مساحت زیر نمودار نیروی برشی از نیمه اول DB تا مفصل B نیز بیانگر کاهش گشتاور خمشی به اندازه 24lb*6ft=-144lb-ft- است. به این ترتیب، مقدار گشتاور خمشی در نزدیکی نقطه B به عدد 528lb-ft=-384-144- میرسد.


نیروها و گشتاورهای موجود در هر مقطع دلخواه را میتوان با استفاده از نمودار جسم آزاد یک سمت آن مقطع به دست آورد. از اینرو، رسم صحیح نمودار جسم آزاد به عنوان یکی از مراحل مهم در تحلیل تیرها به شمار میرود. به کارگیری روابط تفاضلی و هندسی بین بار، نیروی برشی و گشتاور خمشی نیز روش مناسبی برای رسم نمودارهای V ،N و M و تعیین محل رخ دادن مقادیر مثبت هر یک از پارامترها است. نوشتن توابع نیروی محوری، نیروی برشی و گشتاور خمشی معمولاً برای تحلیل سازههای ساده با شرایط بارگذاری ساده به کار میرود.
^^











سلام، باتشکر از مطالب مفیدی که آموزش می دید.
لطف می کنید در متن زیر trajectory را توضیح دهید.
a trajectory of axial force is applied horizontally
.at the cross-section
سلام، ضمن تشکر از اینکه چنین مطالب ارزنده ای جهت یادگیری هموطنان عزیز در سایت قرارمی دهید.اینجانب کارشناس ارشد عمران هستم، واقعا کارتان خوشم امد. ای کاش فایل ورد آن هم در اختیار عموم می گذاشتید.انشالله همیشه تندرست و خوش باشد.
سلام. با تشکر از زحمات شما
در مثال اول روابط بخش دوم و سوم یکی می باشد. لطفا اصلاح فرمایید