خطای حالت ماندگار — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

در آموزشهای پیشین مجله فرادرس، مباحث مربوط به نمایش سیستمهای کنترل را بیان کردیم. تحلیل و طراحی سیستمهای کنترل، مبتنی بر سه ویژگی مهم پاسخ گذرا، پایداری و خطای حالت ماندگار است. در این آموزش، درباره خطای حالت ماندگار بحث خواهیم کرد.
تعریف خطای حالت ماندگار
«خطای حالت ماندگار» (Steady-State Error)، اختلاف بین ورودی و خروجی سیستم در زمان طولانی () برای یک ورودی آزمون است.
ورودیهای آزمون متداول در جدول زیر آورده شدهاند.
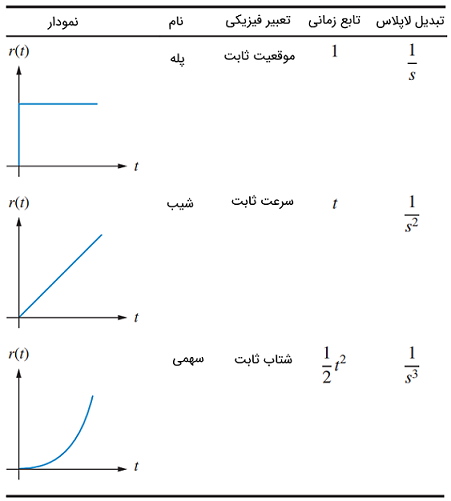
خطای حالت ماندگار را با نشان میدهیم و با استفاده از قضیه مقدار نهایی، داریم:
که در آن تبدیل لاپلاس سیگنال خطای است.
خطای حالت ماندگار هر سیستمی را که اطلاعات آن موجود باشد، میتوان با انجام محاسبات به دست آورد. اما متداول است که فرمول واحد برای سیستم استاندارد با فیدبک واحد استفاده شود. در ادامه، نحوه پیدا کردن خطای حالت ماندگار را برای سیستم با فیدبک واحد و سیستمهای کنترل با فیدبک غیر واحد معرفی میکنیم.
خطای حالت ماندگار برای سیستم با فیدبک واحد
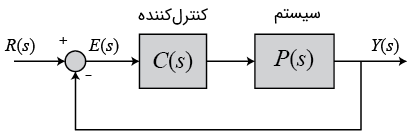
نمودار بلوکی سیستم کنترل حلقهبسته زیر را در نظر بگیرید که فیدبک واحد منفی دارد.
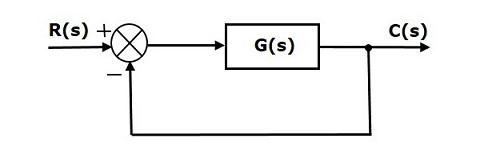
در نمودار بلوکی بالا، تبدیل لاپلاس سیگنال ورودی مرجع ، و تبدیل لاپلاس سیگنال خروجی است.
میدانیم که تابع تبدیل سیستم کنترل با فیدبک واحد منفی به صورت زیر است:
در نتیجه، خروجی سیستم برابر است با:
تابع تبدیل خطای سیستم نیز به صورت زیر است:
با جایگذاری خروجی در معادله خطای اخیر، داریم:
با استفاده از قضیه مقدار نهایی، مقدار خطای حالت ماندگار برابر است با:
جدول زیر، مقدار خطای حالت ماندگار و ثابت انتگرال را برای سیگنالهای ورودی استاندارد مانند پله واحد، شیب واحد و سهمی واحد نشان میدهد.
| سیگنال ورودی | خطای حالت ماندگار | ثابت خطا |
| پله واحد | ||
| شیب واحد | ||
| سهمی واحد |
که در آن ، و به ترتیب، ثابت خطای موقعیت، ثابت خطای سرعت و ثابت خطای شتاب هستند. این ثابتها، ثابت خطای استاتیکی نام دارند.
نکته ۱: اگر هر یک از ورودیهای بالا مقدار دامنهای بیشتر از یک داشته باشد، خطای حالت ماندگار متناظر را در آن ضرب میکنیم.
نکته ۲: نمیتوان خطای حالت ماندگار را برای سیگنال ضربه واحد تعریف کرد، زیرا این سیگنال فقط در صفر تعریف شده است و نمیتوان پاسخ را در زمان بینهایت با آن مقایسه کرد.
مثال
میخواهیم خطای حالت ماندگار سیگنال ورودی را برای سیستم کنترل حلقهبستهای با فیدبک واحد منفی و تابع تبدیل حلقهباز محاسبه کنیم.
سیگنال ورودی، ترکیبی از سه سیگنال پله، شیب و سهمی است. جدول زیر، ثابتهای خطا و مقادیر خطای حالت ماندگار را برای این سه سیگنال نشان میدهد.
| سیگنال ورودی | ثابت خطا | خطای حالت ماندگار |
خطای حالت ماندگار کل، از مجموع خطاهای حالت ماندگار به دست میآید:
بنابراین، خطای خالت ماندگار ، برابر با یک است.
خطای حالت ماندگار برای سیستمهای فیدبک غیر واحد
نمودار بلوکی سیستم کنترل حلقهبسته زیر را در نظر بگیرید که فیدبک غیر واحد منفی دارد.
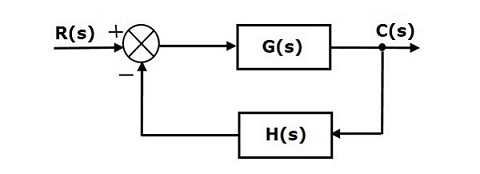
برای جلوگیری از تکرار محاسبات طولانی و استفاده از فرمولهایی که در بالا به دست آوردیم، سیستم فیدبک غیر واحد را به سیستم فیدبک واحد تبدیل میکنیم.
برای این کار، یک مسیر فیدبک واحد مثبت و یک مسیر فیدبک واحد منفی را به نمودار بلوکی اضافه میکنیم. نمودار بلوکی جدید، به صورت زیر درخواهد آمد:
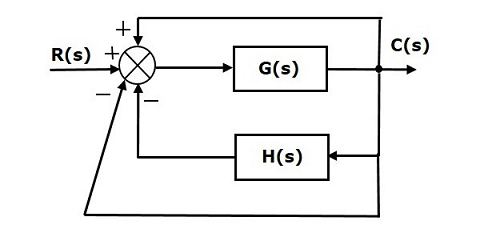
اگر نمودار بالا را با توجه به قواعدی که درباره نمودارهای بلوکی گفتیم، ساده کنیم و فیدبک واحد منفی را نگه داریم، نمودار بلوکی معادل، به صورت شکل زیر خواهد بود.
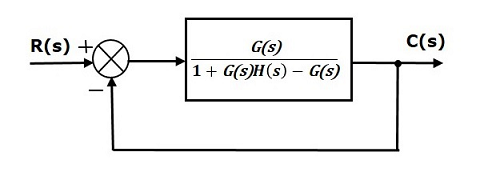
نمودار بلوکی شکل بالا، یک سیستم کنترل حلقهبسته با فیدبک واحد منفی با تابع تبدیل بهجای است. اکنون میتوانیم خطای حالت ماندگار را با استفاده از فرمولهایی که بیان شد محاسبه کنیم.
نوع سیستم و خطای حالت ماندگار
با دانستن ثابتهای خطای استاتیکی و نوع سیستم، میتوان خطای حالت ماندگار را مشخص کرد. «نوع سیستم» (System Type)، به عنوان تعداد انتگرالگیرهای خالصی تعریف میشود که در مسیر پیشِروی یک سیستم فیدبک واحد قرار دارند.
اگر نمودار بلوکی سیستم به صورت زیر باشد، نوع سیستم برابر با خواهد بود. اینکه انتگرالگیر بخشی از کنترلکننده یا سیستم باشد، فرقی ندارد.
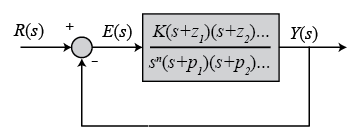
بنابراین، یک سیستم میتواند نوع صفر، نوع یک، نوع دو و غیره باشد. جدولهای زیر، خطای حالت ماندگار را برای سیستمهای نوع صفر، یک و دو نشان میدهند.
| سیستم نوع صفر | ورودی پله | ورودی شیب | ورودی سهموی |
| فرمول خطای حالت ماندگار | |||
| ثابت خطای استاتیکی | ثابت | ||
| خطا | بینهایت | بینهایت |
| سیستم نوع یک | ورودی پله | ورودی شیب | ورودی سهموی |
| فرمول خطای حالت ماندگار | |||
| ثابت خطای استاتیکی | بینهایت | ثابت | |
| خطا | بینهایت |
| سیستم نوع دو | ورودی پله | ورودی شیب | ورودی سهموی |
| فرمول خطای حالت ماندگار | |||
| ثابت خطای استاتیکی | بینهایت | بینهایت | ثابت |
| خطا |
مثال
نمودار بلوکی زیر را در نظر بگیرید.
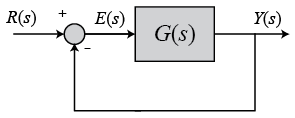
که در آن، تابع تبدیل به صورت زیر است:
از آنجایی که سیستم نوع یک است، خطای حالت ماندگار برای ورودی پله وجود ندارد و برای ورودی سهمی، خطا بینهایت خواهد بود. تنها ورودی که با اعمال آن به سیستم، خطای حالت ماندگار محدود خواهیم داشت، ورودی شیب است. میخواهیم را به گونهای تعیین کنیم که خطای حالت ماندگار سیستم حلقهبسته برای ورودی مرجع شیب، برابر با باشد. ابتدا بهره را با استفاده از نرمافزار متلب بررسی میکنیم:
1s = tf('s');
2G = ((s+3)*(s+5))/(s*(s+7)*(s+8));
3T = feedback(G,1);
4t = 0:0.1:25;
5u = t;
6[y,t,x] = lsim(T,u,t);
7plot(t,y,'y',t,u,'m')
8xlabel('Time (sec)')
9ylabel('Amplitude')
10title('Input-purple, Output-yellow')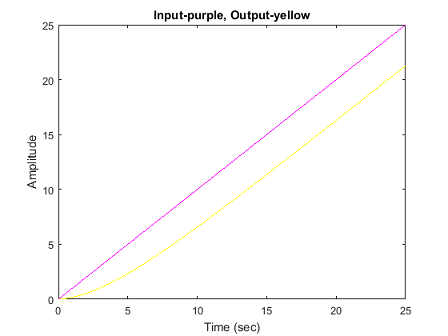
همانطور که میبینیم، خطای حالت ماندگار این سیستم بسیار بزرگ است، زیرا در زمان ثانیه ، خروجی تقریباً و ورودی است (خطای حالت ماندگار تقریباً برابر با است). مسئله را به شکل دیگری حل میکنیم.
همانطور که میدانیم، خطای حالت ماندگار باید برابر با باشد. بنابراین، برای حل مسئله داریم:
اکنون پاسخ به ورودی شیب را برای بررسی میکنیم:
1K = 37.33 ;
2s = tf('s');
3G = (K*(s+3)*(s+5))/(s*(s+7)*(s+8));
4sysCL = feedback(G,1);
5t = 0:0.1:50;
6u = t;
7[y,t,x] = lsim(sysCL,u,t);
8plot(t,y,'y',t,u,'m')
9xlabel('Time (sec)')
10ylabel('Amplitude')
11title('Input-purple, Output-yellow')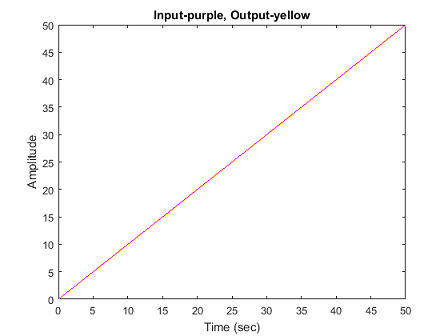
برای آنکه دید بهتری داشته باشیم، بزرگنمایی پاسخ را میبینیم. بدین منظور، پاسخ را بین زمانهای و ثانیه انتخاب میکنیم:
1axis([39.9,40.1,39.9,40.1])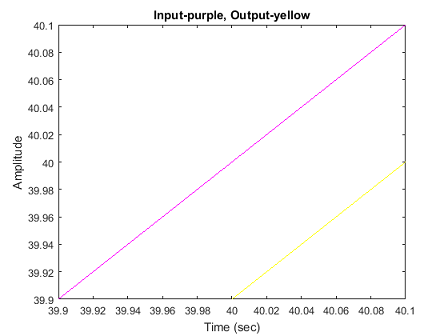
اگر محاسبات مربوط به شکل بالا را انجام دهیم، میبینیم که خطای حالت ماندگار، دقیقاً همان مقدار مطلوب است.
اکنون مسئله را به صورت زیر تغییر میدهیم:
اکنون میخواهیم را به گونهای تعیین کنیم که برای یک ورودی پله، به خطای حالت ماندگار صفر برسیم.
با توجه به جدولهایی که ارائه کردیم، ميتوان گفت که خطای حالت ماندگار سیستم نوع دو به ورودی شیب، برابر با صفر است. بنابراین، میتوان با اضافه کردن یک انتگرالگیر (یک قطب در مبدأ)، به سادگی خطای حالت ماندگار را صفر کرد.
1s = tf('s');
2P = ((s+3)*(s+5))/(s*(s+7)*(s+8));
3C = 1/s;
4sysCL = feedback(C*P,1);
5t = 0:0.1:250;
6u = t;
7[y,t,x] = lsim(sysCL,u,t);
8plot(t,y,'y',t,u,'m')
9xlabel('Time (sec)')
10ylabel('Amplitude')
11title('Input-purple, Output-yellow')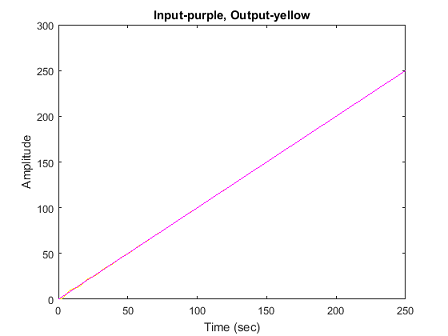
اگر مقداری بزرگنمایی کنیم، میبینیم که اندکی نوسان وجود دارد. البته در حالت ماندگار، خطا مطابق انتظار برابر با صفر است. شکل زیر، پاسخ حول ثانیه را نشان میدهد.
1axis([239.9,240.1,239.9,240.1])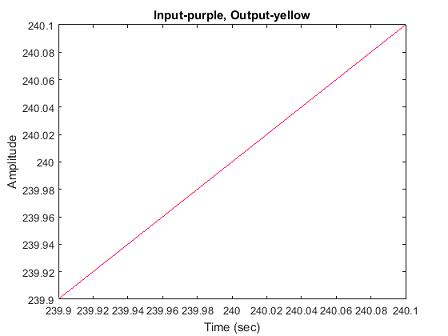
همانطور که میبینیم، خطای حالت ماندگار صفر است.
نکته: خطای حالت ماندگار برای سیستمهای کنترل حلقهبسته ناپایدار، بیمعنی است و فقط برای سیستمهای کنترل حلقهبسته پایدار محاسبه میشود. این بدین معنی است که باید پایداری هر سیستم کنترل را قبل از یافتن خطای حالت ماندگار بررسی کرد.
در صورتی که مباحث بیانشده برای شما مفید بوده و میخواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
- سیستم کنترل حلقه باز — به زبان ساده
- مکان هندسی ریشه ها (Root Locus) در مهندسی کنترل — به زبان ساده
- تقلبنامه (Cheat Sheet) تبدیل لاپلاس
^^













سلام خسته نباشید.ممنون از مطالب مفیدتون.ممنونتون میشم اگه بفرمایید کدام حالت offsetخطای بیشتری داره؟واینکه برای جلوگیری از آن باید چیکار کنیم؟
بسیار عالی و مفید