حل معادلات دیفرانسیل با ماتریس نمایی – به زبان ساده

در این مطلب قصد داریم تا روشی متفاوت به منظور حل معادلات دیفرانسیل همگن را معرفی کنیم. بدین منظور پیشنهاد می‌کنیم ابتدا مطالب معادلات دیفرانسیل و مقدار ویژه و بردار ویژه را مطالعه فرمایید.

تعریف توان در ماتریس‌ها

ماتریس $$A$$ از مرتبه $$n × n$$ را به نحوی در نظر بگیرید که مولفه‌های آن حقیقی یا مجازی هستند. با توجه به مربعی بودن این ماتریس، توان‌های مختلف آن برابر است با:

$$\large \begin {align*} { { A ^ 0 } = I,\;\;{ A ^ 1 } = A,\;\;} & \kern-0.3pt { { A ^ 2 } = A \cdot A,\;\;} \\\\ & \kern-0.3pt { { A ^ 3 } = { A ^ 2 } \cdot A,\; \ldots ,} \\\\ & \kern-0.3pt { { A ^ k } = \underbrace { A \cdot A \cdots A}_\text {k times} } \end {align*}$$

در رابطه فوق $$I$$ نشان دهنده ماتریس همانی از مرتبه $$n$$ است. هم‌چنین در ادامه حاصل جمع ماتریس‌های نمایی را به صورت زیر در نظر می‌گیریم.

$$\large \begin {align*} I + \frac { t } { { 1 ! } } A + \frac { { { t ^ 2 } } } { { 2 ! } } { A ^ 2 } & + { \frac { { { t ^ 3 } } } { { 3 ! } } { A ^ 3 } + \cdots } \\\\ & + { \frac { { { t ^ k } } } { {k ! } } { A^ k } + \cdots } \end {align*}$$

حاصل جمع فوق را ماتریس نمایی نامیده و آن را با $$e ^ { t A }$$ نمایش می‌دهند. این حاصل جمع در ادامه بازنویسی شده است.

$$\large { e ^ { t A } } = \sum \limits _ { k = 0 } ^ \infty {\frac { { {t ^ k } }} { { k ! } } { A ^ k } }$$

سری فوق مطلقا همگرا است. در حالتی حدی زمانی که ماتریس تنها یک عددِ $$a$$ باشد، در این صورت مرتبه ماتریس برابر با $$1×۱$$ است. در این حالت می‌توان از بسط مک لورن به صورت زیر استفاده کرد.

$$\large \begin {align*} e ^ { a t } & = 1 + at + \frac { { { a ^ 2 } { t ^ 2 } } } { { 2! } } + \frac { { { a ^ 3 } { t ^ 3 } } } { { 3! } } + \cdots \\\\ & = { \sum \limits _ { k = 0 } ^ \infty {\frac{ { {a ^ k } { t ^ k } } } { {k ! } } } } \end {align*}$$

توجه داشته باشید که ماتریس نمایی فوق دارای ویژگی‌های زیر است.

• اگر $$A$$، ماتریس صفر باشد، در این صورت رابطه $${ e ^ { t A } } = { e ^ 0 } = I$$ برقرار خواهد بود.
• اگر $$A$$ دارای ماتریس معکوسی همچون $$A ^ { - 1 }$$ باشد، در این صورت رابطه $${ e ^ A } { e ^ { – A } } = I$$ بین ماتریس اصلی و ماتریس معکوس برقرار است.
• ضرب نمایی $${ e ^ { m A } } { e ^ { n A } } = { e ^ { \left ( { m + n } \right ) A } }$$ در این حالت نیز برقرار است. توجه داشته باشید که $$m,n$$ نشان دهنده دو عدد صحیح یا مختلط هستند.
• مشتق ماتریس مطابق با رابطه زیر بدست می‌آید.
  $$\frac { d } { { d t } } \left ( { { e ^ { t A } } } \right ) = A { e ^ { t A } }$$
• اگر $$H$$ یک تبدیل غیر خطی باشد، در این صورت رابطه زیر بین تبدیلات برقرار خواهد بود.
  $$\large {A = H M { H ^ { – 1 } } \Rightarrow \ \ { e ^ { t A } } = H { e ^ { t M } } { H ^ { – 1 } }}$$

در ادامه و در قالب مثال با این تبدیل بیشتر آشنا خواهید شد.

ماتریس نمایی در حل معادلات دیفرانسیل خطی

می‌توان از روش ماتریس نمایی به منظور حل سیستم دستگاه معادلات دیفرانسیل استفاده کرد. بدین منظور در اولین قدم سیستمی از دستگاه معادلات دیفرانسیل را در نظر بگیرید. این سیستم را می‌توان به صورت ماتریسی، به شکل زیر بیان کرد:

$$\large \mathbf { X } ^ { \prime } \left ( t \right ) = A \mathbf { X } \left ( t \right )$$

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

پاسخ عمومی سیستم فوق را می‌توان در قالب ترم‌های توان نمایی ماتریس، به صورت زیر بیان کرد:

$$\large \mathbf { X } \left ( t \right ) = { e ^ { tA } } \mathbf { C }$$

در رابطه فوق $$\mathbf { C } = { \left ( { { C _ 1} , { C _ 2 } , \ldots , { C _ n } } \right ) ^ T }$$ نشان دهنده برداری با $$n$$ مولفه است. بدیهی است که نماد $$T$$ نشان دهنده ترانهاده است. توجه داشته باشید که نوشتن حاصل‌ضرب فوق به صورت زیر اشتباه است.

$$\large \mathop { \mathbf { C } } \limits _ { \left[ { n \times 1 } \right]} \mathop { { e ^ { t A } } } \limits _ { \left[ {n \times n} \right] }$$

برای مسئله‌ای از جنس مقدار اولیه، مولفه‌های $$C$$ به صورت مقدار اولیه بیان می‌شوند. نهایتا حاصل پاسخ همگن را می‌توان به صورت زیر در نظر گرفت.

$$\large { \mathbf { X } \left ( t \right ) = { e ^{ t A } } { \mathbf { X } _ 0 } \;\;} \kern-0.3pt {,\;\;} \kern-0.3pt { { \mathbf { X } _ 0 } = \mathbf { X } \left ( { t = {t_0}} \right ) }$$

بنابراین پاسخ سیستم همگن در صورت معلوم بودن ماتریس نمایی بدست خواهد آمد. به منظور بدست آوردن ماتریس، کافی است از سری بینهایت استفاده کرد.

الگوریتم حل سیستم معادلات دیفرانسیل

در ادامه مراحل حل سیستمی از معادلات دیفرانسیل با استفاده از ماتریس نمایی بیان شده است.

• در ابتدا مقادیر ویژه ($$\lambda _ i$$) ماتریس $$A$$ را بیابید.
• با بدست آمدن مقادیر ویژه، بردار‌های ویژه نیز بدست خواهند آمد.
• با استفاده از بردار‌های ویژه بدست آمده، ماتریس تبدیل $$H$$ را بدست آورید. هم‌چنین بردار معکوس آن یا $$H ^ { - 1 }$$ نیز قابل محاسبه خواهد بود.
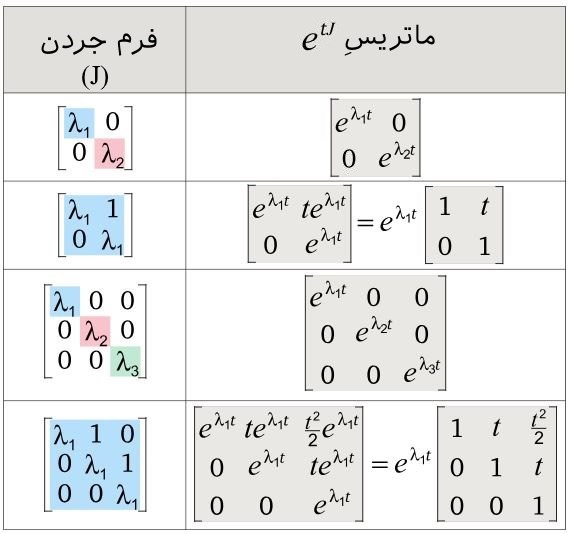
• فرم نرمال جردن را نیز مطابق با رابطه زیر بدست آورید.
  $$J = { H ^ { – 1 } } A H$$
• با بدست آمدن فرم نرمال جردن، ماتریس $${ e ^ { t J } }$$ نیز بدست خواهد آمد. در جدول زیر نحوه چیدن مولفه‌های ماتریس ارائه شده‌اند.

ماتریس نمایی $$e ^ { t A }$$ را با استفاده از رابطه $${ e ^ { t A } } = H { e ^ { t J } } { H ^ { – 1 } }$$ بیابید.

پاسخ عمومی سیستم را به صورت $$\mathbf { X } \left ( t \right ) = { e ^ {t A} } \mathbf { C }$$ در نظر بگیرید. البته برای سیستمی از مرتبه دوم پاسخ باید به صورت زیر در نظر گرفته شود.

$$ \large { \mathbf { X } \left( t \right) = \left[ {\begin{array}{*{20}{ c } } x \\ y \end{array}} \right] } = { { e ^ { t A } } \left[ {\begin{array} {*{20} { c } } { { C _ 1 } } \\ { { C _2 } } \end{array}} \right] } $$

در ادامه مثال‌هایی ذکر شده که با مطالعه آن‌‌ها می‌توانید با حل سیستم‌های معادلات آشنا شوید.

مثال ۱

پاسخ عمومی سیستم زیر را با استفاده از روش ماتریس نمایی بدست آورید.

$$\large { \frac { { d x } } { { d t } } = 2 x + 3 y , \;\;} \kern-0.3pt { \frac { {d y } } { { d t} } = 3 x + 2 y }$$

به منظور پاسخ به این سوال می‌توان از الگوریتم بیان شده در بالا استفاده کرد. بدین منظور در اولین قدم باید مقادیر ویژه را به صورت زیر بدست آورد.

$${{\det \left( { A – \lambda I} \right) }={ \left| {\begin{array}{*{20}{c}}<br /> {2 – \lambda } & 3 \\<br /> 3&{2 – \lambda }<br /> \end{array} } \right| = 0,\;\;}}\\<br /> \Rightarrow<br /> { { \left( {2 – \lambda } \right ) ^ 2 } – 9 = 0,\;\;} \Rightarrow<br /> { 4 – 4\lambda + {\lambda ^2} – 9 = 0,\;\;} \\<br /> \Rightarrow<br /> { { \lambda ^ 2 } – 4\lambda – 5 = 0,\;\;} \Rightarrow<br /> { { \lambda _ 1 } = 5,\;{\lambda _2} = – 1 } $$

بنابراین بردار ویژه مرتبط با مقدار ویژه $${ \lambda _ 1 } = 5$$ برابر است با:

$$ { \left[ {\begin{array}{*{20}{c}} {2 – 5 } & 3\\<br /> 3 & { 2 – 5 } \end {array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{ 1 1 }} }\\ { { V _ { 21} } } \end {array}} \right] = \mathbf{0} }\Rightarrow {\left[ {\begin{array}{*{20}{c}} { – 3 } & 3 \\ 3 & { – 3 } \end{array}} \right]\left[ {\begin{array}{*{20} { c } } { { V _ {1 1 } } } \\ { { V _ { 21 } } } \end {array}} \right] = \mathbf{0}} \Rightarrow<br /> { 3 { V_ { 11 } } – 3 { V_{21}} = 0 } \Rightarrow {{ V _ {1 1} } – {V _ { 21} } = 0 } $$

با قرار دادن $${ V _ { 21 } } = t$$ بردار ویژه $${ \mathbf { V } _ 1 } = { \left ( { { V _ { 11 } } , { V _ { 21 } } } \right ) ^ T }$$ برابر خواهد بود با:

$$ { { V _{ 2 1 } } = t,\;\; }\Rightarrow {{V_{11}} = {V_{21}} = t,\;\;}\Rightarrow<br /> { { \mathbf{V}_1} = \left[ {\begin {array} {*{20}{ c } } { { V _ { 11 } } } \\ { { V _ { 21 } } } \end{array}} \right] = \left[ {\begin {array} {*{20} { c } } t \\<br /> t \end{array}} \right] }={ t\left[ {\begin{array}{*{20} { c } } 1\\ 1 \end{array}} \right] } \sim {\left[ {\begin{array}{*{20}{c}} 1 \\ 1 \end{array}} \right] } $$

به طور مشابه بردار ویژه مرتبط با $${ \lambda _ 2 } = -1$$ نیز برابر است با:

$$ \begin {gather*} { \left[ { \begin {array}{*{20}{c}}<br /> { 2 – \left ( { – 1} \right ) } & 3 \\ 3 & { 2 – \left( { – 1} \right)}<br /> \end {array} } \right] \left[ {\begin{array}{*{20} { c } }<br /> { { V _ { 12 } } } \\ { { V _ { 22 } } } \end{array}} \right] = 0 \;\;} \\ \Rightarrow { \left[ {\begin{array} {*{20}{c}} 3 & 3 \\ 3&3 \end{array} } \right]\left[ {\begin{array} {*{20}{c}}<br /> { { V_{12 } } } \\ { { V _ { 22 } } } \end{array} } \right] = 0 \;\;} \Rightarrow { 3 { V _ {12} } + 3 { V _ {22} } = 0 \;\;} \Rightarrow { { V_ { 12 } } + {V _ { 22 } } = 0 } \end {gather*} $$

با فرض $${ V _ { 22 } } = t$$ دیگر مولفه‌‌های بردار $$V$$ برابرند با:

$$\large { V_ { 12 } } = - { V _ { 22 } }= - t$$

در نتیجه بردار $$V_2$$ برابر است با:

$$\large { { \mathbf{V}_2} = \left[ {\begin{array}{*{20} { c } }<br /> { { V _ { 12 } } } \\ { { V_ { 22 } } } \end{array}} \right] = \left[ { \begin {array} {*{20}{c}}<br /> { – t} \\ t \end{array} } \right] } = {t\left[ {\begin{array}{*{20} { c } } { – 1 } \\<br /> 1 \end {array}} \right] } \sim {\left[ {\begin{array}{*{20} { c } } { – 1 } \\ 1 \end {array}} \right] } $$

از این رو بردار $$H$$ (بردار تبدیلی که از دو بردار ویژه $$V_1$$ و $$V_2$$ بدست آمده) برابر است با:

$$ \large H = \left[ {\begin{array}{*{20} { c } } 1 & { – 1 } \\ 1&1 \end {array} } \right] $$

به همین صورت ماتریس معکوس $$H$$ نیز به صورت زیر بدست خواهد آمد.

$$ \large { \Delta \left ( H \right ) = \left| {\begin{array} {*{20} { c } }<br /> 1& { – 1 } \\ 1&1 \end {array} } \right| } = { 1 + 1 } = { 2 } $$

$$ \large {{H^{ – 1}} }={ \frac { 1 } { { \Delta \left( H \right ) } } { \left[ {\begin{array}{*{20}{ c } } { { H _{ 1 1 } }} & { { H _ { 1 2 } } } \\ { { H _ { 21 } } } & { { H _ { 22 } } } \end{array}} \right]^T} } = {\frac{1}{2}{\left[ {\begin{array}{*{20}{c}} 1&{ – 1} \\ 1&1 \end{array}} \right]^T} } = {\frac { 1 } { 2 } \left[ {\begin{array}{*{20} { c } }<br /> 1 & 1 \\ { – 1 } &1 \end{array}} \right] } $$

با توجه به مقادیر ویژه بدست آمده، فرم جردن برابر است با:

$$ \large {J = \left[ {\begin{array}{*{20}{c}} { { \lambda _ 1 } } & 0 \\ 0 & { { \lambda _ 2 } } \end {array}} \right] }={ \left[ {\begin{array}{*{20} { c } } 5 & 0 \\ 0& { – 1} \end {array}} \right] } $$

البته فرم جردن را می‌توان به صورت زیر و با استفاده از رابطه ماتریس نمایی نیز محاسبه کرد:

$$\begin {align*} { J = {H^{ – 1}}AH } & = {\frac { 1 } { 2 } \left[ {\begin{array}{*{20} { c } } 1&1 \\ { – 1}&1 \end{array}} \right]\left[ {\begin{array}{*{20} { c } } 2 & 3 \\ 3 & 2 \end {array} } \right]\left[ {\begin{array}{*{20} { c } } 1 & { – 1 } \\ 1&1 \end {array} } \right] }<br /> \\\\ & = {\frac { 1 } { 2 } \left[ {\begin{array}{*{20} { c } } 5 & 5 \\ 1&{ – 1} \end {array} } \right]\left[ {\begin{array} {*{20}{c}} 1&{ – 1}\\ 1&1 \end {array}} \right] } \\\\ & = {\frac { 1 } { 2 } \left[ {\begin{array} {*{20}{c}} {5 + 5 } & { – 5 + 5 } \\ {1 – 1} & { – 1 – 1} \end{array}} \right] } \\\\ & = {\frac { 1 } { 2 } \left[ {\begin{array}{*{ 20 } { c } } { 10 } & 0 \\ 0 & { – 2} \end{array}} \right] } = {\left[ {\begin {array}{*{20} { c } } 5 & 0 \\ 0 & { – 1 } \end {array}} \right] } \end {align*} $$

بنابراین ماتریس $${ e ^ { t J } }$$ نیز برابر است با:

$$ \large { e ^ { t J } } = \left[ {\begin{array}{*{20} { c } }<br /> { { e^ { 5 t } } } & 0 \\<br /> 0 & { { e ^ { – t } } }<br /> \end {array} } \right] $$

فیلم آموزش محاسبات عددی با متمتیکا Mathematica – مقدماتی در فرادرس

کلیک کنید

در ادامه به همین صورت ماتریس $${ e ^ { t A } }$$ نیز مطابق با عبارت زیر بدست خواهد آمد.

$$\begin {align*} { { e ^ { t A } } = H { e ^{ t J } } { H ^ { – 1}} } & = {{\left[ {\begin{array}{*{20}{c}} 1&{ – 1} \\ 1&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} { { e ^ { 5 t } } } & 0 \\ 0&{ { e ^ { – t } } } \end{array} } \right] \cdot}\kern0pt{ \frac{1}{2}\left[ {\begin{array}{*{20}{ c } } 1 & 1 \\ { – 1 } & 1 \end {array}} \right] } } \\\\ & = {\frac { 1 } { 2 } \left[ { \begin{array}{*{20}{c}} { { e ^ { 5 t } } } & { – { e ^ { – t } } } \\ { { e ^{ 5 t } } } & { { e^ { – t } } } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&1\\ { – 1}&1<br /> \end{array}} \right] } \\\\ & = {\frac{1}{2}\left[ {\begin{array}{*{20}{c}}<br /> { { e ^{ 5 t } } + { e ^ { – t } } } & { { e ^{ 5 t } } – { e ^ { – t } } } \\<br /> {{ e^ { 5 t} } – { e ^ { – t } } } &{ { e ^{ 5 t } } + { e ^ { – t } } }<br /> \end{array}} \right] } \end {align*} $$

از طرفی پاسخ عمومی سیستم معادلات را نیز می‌توان به شکل زیر بیان کرد:

$$ \large { \mathbf { X } \left ( t \right) = \left[ {\begin{array}{*{20}{ c } } x \\ y \end {array}} \right] } = {{e^{tA}}\left[ {\begin{array}{*{20}{ c } } { { C _ 1 } } \\ { { C_2 } } \end {array}} \right] } = { \frac { 1 } { 2 } \left[ {\begin{array}{*{20} { c } } { { e ^ { 5 t } } + { e ^ { – t } } } & { {e ^ { 5 t } } – {e ^ { – t } } } \\ { { e ^ { 5 t } } – {e^{ – t}}}& { { e^ { 5 t } } + {e^{ – t } } } \end{array}} \right]\left[ {\begin{array}{*{20} { c } } { { C _ 1 } } \\ { { C _ 2 } } \end{array}} \right] } $$

همان‌طور که در بالا نیز بیان شد، مقادیر $$C$$ در عبارت فوق اعدادی ثابت هستند که با توجه به شرایط معادله بدست می‌آیند. پاسخ نهایی را می‌توان به صورت زیر نیز بازنویسی کرد:

$$ \begin {align*} {\mathbf { X } \left( t \right) = \left[ {\begin{array}{*{20}{c } } x \\ y \end {array} } \right] } & = { \frac { 1 }{2}\cdot}\kern0pt { \left[ {\begin{array}{*{20} { c } } { { C _ 1 }{e^{5t}} + { C _ 1 } { e ^ { – t}} \text{+} {C_2}{e^{5t}} – {C_2}{e^{ – t } } } \\ { { C _ 1 } { e ^ { 5 t } } – {C_1}{e^{ – t}} \text{+} {C_2}{e^{5t}} + { C _ 2 } { e ^ { – t } } } \end{array}} \right] } \\\\ & = {\frac{1}{2}\cdot}\kern0pt{\left[ {\begin{array} {*{20} { c } } {{e^{5t}}\left( {{C_1} + {C_2}} \right) + {e^{ – t } } \left( {{C_1} – {C_2}} \right)}\\ {{e^{5t}}\left ( { { C _ 1 } + {C_2}} \right ) – { e ^ { – t}}\left( {{C_1} – {C_2}} \right)} \end{array}} \right] } \\\\ & = {\frac { 1 } { 2 } \left( { { C _ 1 } + { C _ 2 } } \right) { e ^ { 5 t } } \left[ {\begin{array}{*{20}{c}} 1 \\ 1 \end{array}} \right] }+{ \frac { 1 }{2}\left( { { C _ 1 } + { C _ 2 } } \right ) { e^ { – t } } \left[ {\begin{array}{*{20}{c}} 1 \\ 1 \end{array} } \right] } \\\\ & = { { B _ 1 } { e ^ {5 t} } \left[ {\begin{array} {*{ 20 } { c } } 1 \\ 1 \end {array}} \right] + { B _ 2 } { e ^ { – t} }\left[ {\begin{array}{*{20}{c}} 1 \\ 1 \end{array}} \right] } \end {align*} $$

در عبارت بازنویسی شده‌ در بالا، ضرایب $$B$$ نیز اعدادی ثابت هستند که وابسته به ضرایب $$C$$اند.

مثال ۲

با استفاده از روش ماتریس نمایی سیستم معادلات زیر را حل کنید.

$$\large { \frac { { d x} } { { d t } } = 4 x \;\; ,\;\;} \kern-0.3pt { \frac { { d y} } { { d t } } = x + 4 y }$$

معادله مشخصه مربوط به سیستم فوق و مقادیر ویژه آن برابرند با:

$$ { { \det \left ( { A – \lambda I} \right ) } = { \left| {\begin{array}{*{20} { c } } { 4 – \lambda }&0\\ 1 & { 4 – \lambda } \end {array}} \right| = 0,\;\;} } \Rightarrow { { \left ( { 4 – \lambda } \right ) ^ 2 } = 0,\;\;}\Rightarrow { { \lambda _1 } = 4 } $$

بنابراین برای این سیستم تنها یک مقدار ویژه تکراری یافت شد ($$\lambda =4,4$$). بردار ویژه $${ \mathbf { V } _ 1 } = { \left ( { { V _ {1 1 }} , { V_ { 2 1 } } } \right ) ^ T }$$ برابر است با:

$$ \large {\left[ {\begin{array} {*{20} { c } }<br /> {4 – 4 } & 0 \\ 1 & {4 – 4} \end {array}} \right]\left[ { \begin {array} {*{20} { c} } { { V _ { 11 } } } \\ {{V_{21}}} \end{array}} \right] = \mathbf {0 } ,\;\;} \Rightarrow {\left[ {\begin{array}{*{20}{c}}<br /> 0&0\\ 1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{11 } } } \\ {{V_{21 } } } \end{array}} \right] = \mathbf{0},\;\;}\Rightarrow {1 \cdot {V_{11}} + 0 \cdot {V_{21}} = 0 } $$

معادله فوق به ما می‌گوید که $$V _ { 12 }$$ برابر با صفر است؛ از طرفی مقدار $$V _ { 11 }$$ می‌تواند هر عدد دلخواهی باشد. به منظور ۱ بودن اندازه بردار مقدار $$V _ { 12 }$$ را برابر با ۱ انتخاب می‌کنیم. نهایتا بردار ویژه $${ \mathbf { V } _ 1 }$$ برابر می‌شود با:

$$\large { \mathbf { V} _ 1 } = { \left ( { 0 , 1 } \right ) ^ T }$$

بردار مستقل دوم که به صورت $${\mathbf { V } _ 2 } = { \left ( { { V _ { 12 } } , { V_ { 22 } } } \right ) ^ T }$$ در نظر گرفته می‌شود، نیز با استفاده از دستگاه معادلاتی که در ادامه ذکر شده، بدست می‌آید.

$$ \large { \left( {A – { \lambda _ 1 } I } \right ) { \mathbf { V } _ 2 } = {\mathbf { V } _ 1 }, \;\;}\Rightarrow {\left[ {\begin{array}{*{20}{c}}<br /> 0&0\\ 1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{12 } } } \\ {{V_{22 } } } \end{array}} \right] = \left[ {\begin{array}{*{20 } { c} } 0 \\ 1 \end{array}} \right],\;\;}\Rightarrow {\left\{ {\begin{array}{*{20} { l } } { 0 \cdot { V _ { 12 } } + 0 \cdot {V_{22}} = 0}\\ {1 \cdot { V _{ 1 2 } } + 0 \cdot { V_ { 22 } } = 1} \end{array}} \right..} $$

در معادله فوق نیز مقدار $$V_{22}$$ هر عددی می‌تواند باشد. نهایتا به منظور سادگی، مقادیر زیر در نظر گرفته می‌شوند.

$$\large V _{ 22 } = 0 \ , \ V _{ 11 } = 0$$

بنابراین نهایتا بردار $$V_2$$ برابر می‌شود با:

$${ \mathbf { V } _ 2 } = { \left ( { 1 , 0 } \right ) ^ T }$$

حال با استفاده از بردار‌های پایه، ماتریس $$H$$ برابر خواهد بود با:

$$ H = \left[ {\begin{array}{*{20} { c } }<br /> 0&1 \\ 1 & 0 \end {array}} \right] $$

هم‌چنین بردار معکوسِ $${ H ^ { – 1 } }$$ برابر است با:

$$ { { \Delta \left( H \right) = \left| {\begin{array}{*{20}{c}}<br /> 0 & 1 \\ 1 & 0 \end {array} } \right| }={ 0 – 1 = – 1,\;\;}}\kern-0.3pt<br /> { { H ^ { – 1}} = \frac{1} { { \Delta \left( H \right ) } } { \left[ {\begin{array}{*{20 } { c }} { { H _ { 1 1}}}&{{H_{ 12 } } } \\ { { H _ { 2 1 } } } & { { H _ {22 } } } \end{array} } \right] ^T } } $$

در این ماتریس مقادیر $$H_{ij}$$ کوفاکتور‌های ماتریس $$H$$ است. پس از محاسبه، معکوسِ $$H$$ برابر می‌شود با:

$$ \large { { H ^ { – 1 } } = \frac { 1 } { { \left( { – 1} \right)}}{\left[ {\begin{array}{*{20}{c}} 0&{ – 1 } \\ { – 1}&0 \end{array}} \right]^T} } = {\left( { – 1} \right)\left[ {\begin{array}{*{20}{c}} 0&{ – 1}\\<br /> { – 1}&0 \end{array}} \right] } = { \left[ {\begin{array}{*{20}{c}} 0&1\\ 1&0 \end{array}} \right] } $$

به شکلی تصادفی اتفاقی جالب رخ داده است؛ چرا که دو تابعِ $$H$$ و $$H ^ { - 1 }$$ برابر با یکدیگر بدست آمده‌اند. این اتفاق زمانی رخ می‌دهد که توان دوم یک ماتریس برابر باشد با:

$$ \large { { H ^ 2 } = {\left[ {\begin{array}{*{20}{c}}<br /> 0 & 1 \\ 1 & 0 \end {array} } \right] ^ 2 } }<br /> = {\left[ {\begin {array} {*{20} { c } } 0 &1 \\ 1 & 0 \end{array}} \right]\left[ { \begin {array}{*{ 20 } { c } } 0&1\\ 1 & 0 \end{array}} \right] } = {\left[ { \begin {array} {*{20}{c}} {0 + 1 } & { 0 + 0 } \\ {0 + 0}&{1 + 0} \end{array}} \right] } = { \left[ { \begin {array} {*{20} { c } } 1& 0 \\ 0 &1 \end {array}} \right] = I } $$

فرم جردن یا همان $$J$$ مربوط به ماتریس $$A$$ نیز برابر است با:

$$\begin {align*} { J = { H ^ { – 1 } } A H } & = { \left[ { \begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right]\left[ {\begin {array}{*{20}{c}} 4&0\\ 1&4 \end{array}} \right]\left[ {\begin {array}{*{20}{c}} 0&1\\ 1 & 0 \end{array}} \right] } \\\\ & = {\left[ {\begin{array}{*{20}{c}} {0 + 1 } & { 0 + 4 } \\ {4 + 0 } & { 0 + 0 } \end {array} } \right]\left[ {\begin {array}{*{20}{ c } } 0 & 1 \\ 1&0 \end {array} } \right] } \\\\ & = {\left[ {\begin{array}{*{20} { c } } 1 & 4\\ 4 & 0 \end{array}} \right]\left[ {\begin{array}{*{20} { c } } 0 & 1 \\ 1&0 \end {array} } \right] } \\\\ & = { \left[ {\begin {array} {*{20}{c}} { 0 + 4 } & { 1 + 0 } \\ {0 + 0}&{4 + 0} \end{array}} \right] } = {\left[ {\begin{array}{*{20}{c}} 4 & 1 \\ 0& 4 \end{array}} \right] } \end {align*} $$

با بدست آمدن فرم جردن، ماتریس تبدیل نیز برابر خواهد بود:

$$ \large { { e ^ { t J } } = \left[ {\begin{array}{*{20}{c}}<br /> { { e ^{ 4 t } } } & { t { e ^ { 4 t } } } \\ 0&{{e^{4t}}}<br /> \end {array}} \right] }={ { e ^ {4 t } } \left[ {\begin{array}{*{20} { c } } 1& t \\ 0&1 \end{array}} \right] }$$

در نتیجه ماتریس نمایی نیز برابر است با:

$$\begin {align*} { { e ^ { t A } } = H { e ^ { t J } } { H ^ { – 1 } } } & = { { e ^ { 4 t } } \left[ { \begin {array} {*{20} { c } } 0 & 1 \\ 1 & 0 \end {array} } \right] \left[ { \begin {array} {*{20}{c}} 1 & t \\ 0&1 \end {array}} \right] \left[ {\begin{array}{*{20}{c}} 0 & 1 \\ 1&0 \end{array}} \right] } \\\\ & = {{e^{4t}}\left[ {\begin{array}{*{20}{c}} {0 + 0}&{0 + 1 } \\ {1 + 0}&{t + 0} \end{array}} \right]\left[ {\begin{array}{*{20} { c } } 0 & 1 \\ 1 & 0 \end{array}} \right] } \\\\ & = {{e^{4t}}\left[ {\begin{array}{*{20}{c}} 0& 1 \\ 1&t \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 0 & 1 \\ 1 & 0 \end{array}} \right] } \\\\ & = {{e^{4t}}\left[ {\begin{array}{*{20}{c}} {0 + 1 } & { 0 + 0 } \\ {0 + t}&{1 + 0} \end{array}} \right] } = {{e^{4t}}\left[ { \begin{array}{*{20}{c}} 1&0 \\ t&1 \end{array}} \right] } \end {align*} $$

بنابراین نهایتا پاسخ عمومی سیستم برابر می‌شود با:

$$ \large { \mathbf{X}\left( t \right) = \left[ {\begin{array}{*{20}{c}}<br /> x \\ y \end {array}} \right] = { e ^ { t A } } \mathbf{C} }<br /> = { { e ^ { 4 t } } \left[ {\begin {array} {*{20}{c}}<br /> 1 & 0 \\ t & 1 \end {array}} \right] \left[ {\begin{array}{*{20}{c}}<br /> { { C _ 1 } } \\ { { C _ 2 } } \end {array}} \right] } $$

مثال ۳

سیستم معادلات زیر را با استفاده از روش ماتریس نمایی حل کنید.

$$\large { \frac { { d x } } {{ d t } } = x + y \; ,\;\;} \kern-0.3pt {\frac { {d y } } {{ d t } } = – x + y }$$

بدیهی است که برای این سیستم ماتریس $$A$$ برابر است با:

$$\large A = \left [ {\begin{array} {*{20} { c } } 1 & 1 \\ { – 1 } & 1 \end {array} } \right] $$

بنابراین مقادیر ویژه این ماتریس نیز برابرند با:

$$ \begin {align*} {{\det \left( {A – \lambda I} \right) } = { \left| {\begin{array}{*{20} { c } } {1 – \lambda } & 1 \\ { – 1}&{1 – \lambda } \end{array}} \right| = 0 \;\;} } & \Rightarrow { { \left( {1 – \lambda } \right)^2} + 1 = 0 \;\;} \\\\ & \Rightarrow {{\left( {\lambda – 1} \right)^2} = – 1 \;\;} \\\\ & \Rightarrow { \lambda – 1 = \pm i \;\;} \Rightarrow {{\lambda _{1,2}} = 1 \pm i } \end {align*} $$

بنابراین ماتریسِ $$A$$ دو ریشه مختلط دارد. برای هریک از این مقادیر ویژه باید برداری ویژه نیز نسبت داد. بدین منظور $${ \mathbf { V } _ 1 } = { \left ( { { V _ { 11 } }, { V _ { 21 } } } \right ) ^ T }$$ را که مرتبط با مقدار ویژه $${\lambda _1} = 1 + i$$ است، در نظر بگیرید. مولفه‌های این بردار باید معادله زیر را ارضا کنند.

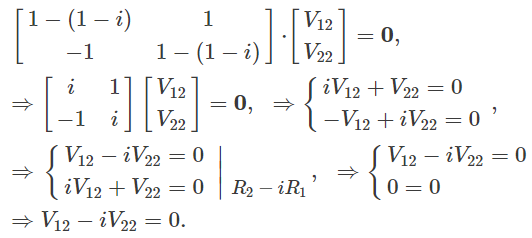
با فرضِ $${ V _ { 21 } } = t$$، مقدار $$V_{21}$$ نیز برابر است با:

$$\large V_{21}=-it$$

بنابراین مقدار $${ \mathbf { V } _ 1 }$$ نیز برابر با عبارت زیر بدست خواهد آمد.

$$ \large { { \mathbf { V } _ 1 } = \left[ {\begin{array}{*{20}{c}}<br /> { { V _ { 11 } } } \\ { { V _ { 21 } } } \end{array}} \right] = \left[ { \begin {array}{*{20} { c } } { – i t } \\ t \end {array} } \right] } = {t\left[ {\begin{array}{*{20} { c } } { – i } \\ 1 \end{array} } \right] } \sim {\left[ {\begin{array}{*{20} { c } } { – i } \\ 1 \end {array} } \right] } $$

به طور مشابه، مولفه‌های بردار ویژه $${\mathbf { V} _ 2 } = { \left( { { V _ { 12 } } , { V _ { 22 } } } \right ) ^ T }$$ مرتبط با $${ \lambda _ 2 } = 1 – i$$ نیز در رابطه زیر صدق می‌کنند.

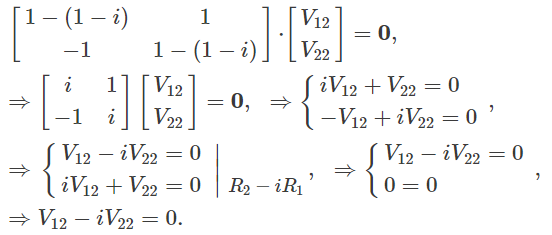
به منظور حل سیستم فوق کافی است از تغییر متغیر $$V _ { 22 } = t$$ استفاده کرد. با استفاده از این تغییر متغیر، دیگر مولفه بردار $$V _ 2$$ برابر با $${ V _ { 12 } } = i t$$ بدست می‌آید. نهایتا بردار $$V _ 2$$ برابر است با:

$$ { { \mathbf { V } _ 2 } = \left[ {\begin{array}{*{20} { c } }<br /> { { V _ { 12 } } } \\ {{V_{22 } } } \end{array}} \right] = \left[ { \begin{array}{*{20} { c} } { i t } \\ t \end {array}} \right] } = {t\left[ { \begin{array}{*{20}{c}} { i } \\ 1 \end{array}} \right] } \sim {\left[ { \begin{array}{*{20}{c } }<br /> { i } \\ 1 \end{array}} \right] } $$

با بدست آمدن بردار‌های ویژه $$V_1$$ و $$V_2$$، بردارهای $$H$$ و $$H^{-1}$$ نیز به صورت زیر بدست خواهند آمد.

$$ \large H = \left[ {\begin{array}{*{20}{c}}<br /> { – i } & i \\ 1 & 1 \end {array} } \right] $$

$$ \large { { H ^ { – 1 } } } = { \frac { 1 } { { \Delta \left ( H \right ) } } { \left[ {\begin{array}{*{20}{ c } } { { H _ { 11 } } } & { { H _{12 } } } \\<br /> { { H _ { 21 } } } & { { H _ { 22 } } } \end{array}} \right]^ T } } $$

توجه داشته باشید که در عبارت فوق، $$Δ ( H )$$، دترمینان و $$H_{ij}$$، کوفاکتور‌های این ماتریس را نشان می‌دهند. بنابراین ماتریس معکوس $$H$$ نیز برابر است با:

$$ \large { \Delta \left( H \right) = \left| {\begin{array}{*{20} { c } }<br /> { – i } & i \\ 1 & 1 \end {array} } \right| } = { – i – i } = { – 2 i } $$

$$ \large { { H ^ { – 1 } } = \frac { 1 } { { \left( { – 2 i } \right ) } } { \left[ {\begin{array}{*{20} { c } } 1 & { – 1 } \\ { – i} & { – i } \end{array}} \right]^T} } = {\frac { 1 } { { \left( { – 2 i } \right ) } } \left[ {\begin{array}{*{20}{c}} 1 & { – i } \\ { – 1 } & { – i} \end {array}} \right] } = {\frac{1}{{2i}}\left[ { \begin {array} {*{20} { c } } { – 1 } & i \\ 1 & i \end {array} } \right] } $$

بنابراین فرم جردن که با رابطه $$J = { H ^ { – 1 } } A H$$ بدست می‌آید نیز برابر است با:

$$ \begin {align*} { { J = \frac { 1 }{{2i}}\left[ {\begin{array}{*{20}{c}} { – 1 } & i \\ 1 & i \end{array}} \right]\left[ { \begin{array}{*{20}{c}} 1&1 \\ { – 1 } & 1 \end {array}} \right] \cdot}\kern0pt{ \left[ {\begin{array}{*{20} { c } } { – i } & i \\ 1&1 \end {array}} \right] }} & = { { \frac { 1 } { { 2 i } } \left[ {\begin{array}{*{20}{c}}<br /> { – 1 – i} & { – 1 + i } \\ {1 – i} & {1 + i} \end{array}} \right] \cdot}\kern0pt{ \left[ {\begin{array}{*{20}{c}}<br /> { – i}&i\\ 1&1 \end {array}} \right] } } \\ & = {\frac { 1 } { {2 i } }\left[ {\begin{array}{*{20}{c}} {2i – 2}& 0 \\ 0&{2i + 2} \end{array}} \right] } \\ & = {\left[ {\begin{array}{*{20}{c}} {\frac { { i – 1 } } { i } } & 0 \\ 0 & { \frac { { i + 1 } } { i } } \end {array}} \right] } \\ & = {\left[ { \begin{array}{*{20} { c } } { 1 + i } & 0 \\ 0 & { 1 – i } \end {array}} \right] } \end {align*} $$

بنابراین ماتریس $$e^{tJ}$$ برابر می‌شود با:

$$ \large { { e^ { t J } } = \left[ {\begin{array}{*{20} { c } } { { e ^ { \left( { 1 + i } \right ) t } } } & 0 \\ 0 & { { e ^ { \left( {1 – i } \right ) t } } } \end{array}} \right] } = { \left[ {\begin {array}{*{20} { c } } { { e ^ t } { e ^ { i t } } } & 0 \\ 0 & { { e ^ t } { e ^ { – i t } } } \end{array}} \right] } = { { e ^ t } \left[ {\begin{array}{*{20} { c } } { { e ^ { i t} } } & 0 \\ 0 & { { e ^ { – i t } } } \end{array}} \right] } $$

بنابراین ماتریس نمایی برابر است با:

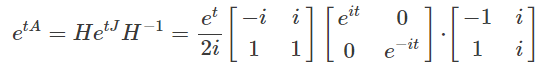
نهایتا توابع نمایی را می‌توان با استفاده از فرمول اویلر به صورت زیر بدست آورد.

$$\large { { e ^ { i t } } = \cos t + i \sin t \;\; ,\;\;} \kern-0.3pt { { e ^ { – i t } } = \cos t – i \sin t }$$

با استفاده از توابع فوق، نهایتا ماتریس نمایی برابر به صورت زیر بدست خواهد آمد.

$$\begin {align*} \require{cancel} { { e ^ { t A } } \text{ = } } & \kern0pt { { \frac { { { e ^ t } } } { { 2 i } } \left[ {\begin{array}{*{20}{c}} { – i}& i \\ 1&1 \end {array}} \right] \cdot}}\kern0pt{{ \left[ {\begin{array}{*{20} { c } } {\cos t + i\sin t}&0\\ 0&{\cos t – i\sin t}<br /> \end{array}} \right] \cdot} } \kern0pt{{ \left[ {\begin{array}{*{20}{c}} { – 1}&i\\ 1&i \end{array}} \right] }} \\ & = { { \frac { { {e ^ t } } } { {2 i } }\cdot}}\kern0pt{{\left[ {\begin{array}{*{20}{c}} { – i\cos t + \sin t}&{i\cos t + \sin t } \\ {\cos t + i\sin t}&{\cos t – i\sin t} \end{array}} \right] \cdot}}\kern0pt{{ \left[ {\begin{array}{*{20}{c}}<br /> { – 1}&i\\ 1&i \end{array} } \right] } } \\ & = { \frac { { { e ^ t } } } { { 2 i } } \left[ {\begin{array}{*{20}{c}} {2i\cos t}&{ 2 i \sin t } \\ { – 2i\sin t}&{2i\cos t } \end{array}} \right] } \\ & = {{e^t}\left[ {\begin{array}{*{20}{c}} {\cos t}&{\sin t } \\ { – \sin t } & { \cos t } \end{array}} \right] } \end {align*} $$

بنابراین پاسخ عمومی این معادله نیز نهایتا برابر با بردار زیر بدست می‌آید.

$$\large{\mathbf{X}\left( t \right) = \left[ {\begin{array}{*{20}{c}}<br /> x \\ y \end{array}} \right] = {e^{tA}}\mathbf{C} }<br /> = {{e^t}\left[ {\begin{array}{*{20} { c } } { \cos t}&{\sin t } \\ { – \sin t}&{\cos t} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{C_1}}\\ {{C_2}} \end{array}} \right] } $$

بدیهی است که بردار $$C = { \left ( { { C _ 1 } , { C _ 2} } \right ) ^ T }$$، برداری ثابت محسوب می‌شود. معمولا این ضریب را با استفاده از شرایط اولیه یا شرایط مرزی تعیین می‌کنند.