حد و مشتق تابع مختلط – از صفر تا صد

در مطالب گذشته وبلاگ فرادرس تابع مختلط، را معرفی کردیم. یکی از مفاهیم مهم در مورد این توابع، تحلیلی بودن آن‌ها است. اما قبل از آشنایی با تابع تحلیلی باید با مفهوم حد و مشتق در توابع مختلط آشنا باشید. بنابراین در این مطلب قصد داریم تا نحوه محاسبه حد و مشتق تابع مختلط را توضیح داده و مثال‌هایی نیز از آن ارائه دهیم.

مقدمه

در ریاضیات، مشتق یک تابع مختلط با استفاده از رابطه زیر تعریف می‌شود.

$$f ^ { \prime } ( z ) = \lim _ { \Delta z \rightarrow 0 } \frac { \Delta f } { \Delta z } = \lim _ { \Delta z \rightarrow 0 } \frac { f ( z + \Delta z ) - f ( z ) } { \Delta z }$$

قبل از توضیح کامل در مورد مشتق باید اطلاعاتی در مورد نحوه محاسبه حد داشته باشید. برای نمونه به دو مثالی که در ادامه آمده، توجه فرمایید.

مثال ۱

مشتق تابع مختلط $$f ( z ) = z ^ { 2 }$$ را بیابید.

هدف اصلی از ارائه این مثال، محاسبه مشتق با استفاده از تعریف حد است. بدین منظور داریم:

$$\lim _ { \Delta z \rightarrow 0 } \frac { ( z + \Delta z ) ^ { 2 } - z ^ { 2 } } { \Delta z } = \lim _ { \Delta z \rightarrow 0 } \frac { z ^ { 2 } + 2 z \Delta z + ( \Delta z ) ^ { 2 } - z ^ { 2 } } { \Delta z } = \lim _ { \Delta z \rightarrow 0 } 2 z + \Delta z = 2 z$$

مثال فوق، مثالی آسان محسوب می‌شود. در ادامه مثالی مطرح شده که در محاسبه مشتق آن باید با احتیاط حاصل حد را محاسبه کرد.

مثال ۲

مشتق تابع مختلط $$f ( z ) = \overline { z }$$ را در مبدا بیابید. با استفاده از حد داریم:

$$f ^ { \prime } ( 0 ) = \lim _ { \Delta z \rightarrow 0 } \frac { f ( \Delta z ) - f ( 0 ) }{ \Delta z } = \lim _ { \Delta z \rightarrow 0 } \frac { \overline { \Delta z } } { \Delta z } = \frac { \Delta x - i \Delta y } { \Delta x + i \Delta y }$$

در محاسبه حد فوق از $$\Delta z = \Delta x + i \Delta y$$ استفاده شده است. حال با فرض $$\Delta z \rightarrow 0$$، هر دو مقدار $$\Delta x$$ و $$\Delta y$$ باید به سمت صفر نزدیک شوند. راه‌های زیادی به منظور حرکت روی این مسیر وجود دارد. در این مثال، دو مسیر متفاوت را انتخاب کرده و خواهیم دید که حاصل حد نیز روی آن‌ها متفاوت هستند. در مسیر اول در راستای محور $$x$$ حرکت می‌کنیم. در این راستا تغییرات $$y$$ برابر با صفر بوده ($$\Delta y = 0$$) و مقدار $$\Delta x$$ نیز به صفر نزدیک می‌شود. در نتیجه روی این مسیر می‌توان گفت:

$$f ^ { \prime } ( 0 ) = \lim _ { \Delta x \rightarrow 0 } \frac { \Delta x } { \Delta x } = 1$$

در مسیر دوم فرض کنید در راستای محور $$y$$ حرکت کنیم. در این صورت حاصل حد را می‌توان به صورت زیر بدست آورد.

$$f ^ { \prime } ( 0 ) = \lim _ { \Delta y \rightarrow 0 } \frac { - i \Delta y } { i \Delta y } = - 1$$

همان‌طور که مشاهده می‌شود، دو مسیرِ متفاوت، دو مقدار متفاوت را برای حد نتیجه می‌دهند. از این رو تابع $$f ( z )$$ در نقطه $$z = 0$$ دارای حد نیست. در ادامه مفهوم حد و مشتق را با جزئیات بیشتری توضیح می‌دهیم؛ اما قبل از آن باید با مفهوم دامنه در توابع مختلط آشنا باشید.

دامنه تابع

ناحیه دیسکی، ناحیه‌ای با نقاط قرار گرفته در فاصله $$r$$ از $$z _ 0$$ است. در واقع تمامی نقاط قرار گرفته در $$\left| z - z _ { 0 } \right| < r$$، این نقاط را شامل می‌شوند.

فیلم آموزش ریاضی مهندسی – مرور و حل مساله در فرادرس

کلیک کنید

ناحیه محذوف دیسکی به شعاع $$r$$ و مرکز $$z _ 0$$ نیز ناحیه‌ای است که در آن تمامی نقاط قرار گرفته در فاصله‌ای بسیار اندک از $$z _ 0$$ حذف شده باشند. این ناحیه شامل نقاط $$0 < \left| z - z _ { 0 } \right| < r$$ است.

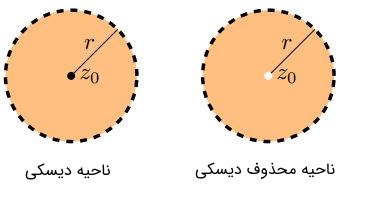
تعریف: یک ناحیه باز در یک صفحه مختلط به مجموعه نقاطی از $$A$$ گفته می‌شود به نحوی که بتوان حول هر نقطه از آن، یک ناحیه دیسکی تعریف کرد. معمولا به شکلی ساده، منطقه مذکور را ناحیه $$A$$ می‌نامیم. برای نمونه در شکل زیر دو ناحیه $$A$$ و $$B$$ نشان داده شده‌اند. توجه داشته باشید که خط‌چین‌ها نشان‌دهنده این موضوع هستند که مرز $$A$$ جزئی از $$A$$ محسوب نمی‌شود. با توجه به این تعریف نمی‌توان به دور تمامی نقاط قرار گرفته در ناحیه $$B$$، یک دایره کشید به نحوی که دایره مذکور در ناحیه $$B$$ قرار داشته باشد. در نتیجه ناحیه $$B$$ یک ناحیه باز محسوب نمی‌شود. این در حالی است که اگر نقطه‌ای را در ناحیه $$A$$ انتخاب کنید می‌توان یک دایره را به نحوی دور آن کشید که تمامی دایره در $$A$$ قرار داشته باشد. در نتیجه می‌توان گفت که تنها $$A$$ یک ناحیه باز محسوب می‌شود.

حد و تابع پیوسته

تعریف: اگر تابع $$f ( z )$$ روی یک ناحیه محذوف در اطراف $$z _ 0$$ تعریف شده باشد، در این صورت در ابتدا حد زیر را در نظر بگیرید.

$$\color {white} {\lim _ { z \rightarrow z _ { 0 } } f ( z ) } \lim _ { z \rightarrow z _ { 0 } } f ( z ) = w _ { 0 } \color {white} {\lim _ { z \rightarrow z _ { 0 } } f ( z ) }$$

اگر مقدار $$f ( z )$$ به سمت $$w _ 0$$ میل کند در این صورت مسیر نزدیک شدن $$z$$ به $$z _ 0$$ مهم نیست. در حقیقت به درستی می‌توان گفت تابع در نقطه مذکور دارای حد است. در شکل زیر حد $$\lim _ { z \rightarrow z _ { 0 } } f ( z ) = w _ { 0 }$$ از چندین مسیر مختلف نشان داده شده است. همان‌طور که مشاهده می‌کنید تمامی این مسیر‌ها در صفحه $$w$$ به نقطه $$w _ 0$$ نزدیک شده‌اند.

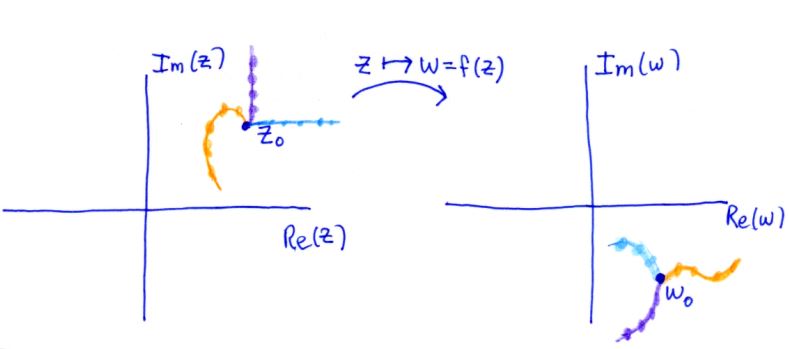
بسیاری از توابع غیرکسری که به صورت چندجمله‌ای هستند، ویژگی فوق را دارند. برای نمونه:

$$\lim _ { z \rightarrow 2 } z ^ { 2 } = 4$$

در ادامه مثالی ارائه شده که برای آن حد در مبدا وجود ندارد.

مثال ۳

نشان دهید که حد زیر موجود نیست.

$$\lim _ { z \rightarrow 0 } \frac { z } { \overline { z } } = \lim _ { z‌ \rightarrow 0 } \frac { x + i y } { x - i y }$$

با حرکت روی محور $$x$$، حاصلِ $$\frac { z } { \overline { z } } = \frac { x } { x } = 1$$ بدست می‌‌آید. بنابراین حاصل حد نیز در این مسیر برابر با $$1$$ است. از طرفی با حرکت روی محور موهومی یا همان محور $$y$$ نیز می‌توان گفت:

$$\frac { z } { \overline { z } } = \frac { i y } { - i y } = - 1$$

همان‌طور که مشاهده می‌کنید با انتخاب دو مسیر متفاوت، دو مقدار متفاوت بدست آمد. بنابراین می‌توان گفت این تابع در نقطه مذکور حدی ندارد.

ویژگی‌های حد

بسیاری از ویژگی‌های حد در توابع مختلط همانند توابع حقیقی است. در ابتدا فرض کنید حد دو تابع $$f$$ و $$g$$ به صورت زیر باشد.

$$\lim _ { z \rightarrow z _ { 0 } } f ( z ) = w _ { 1 } \text { , } \lim _ { z \rightarrow z _ { 0 } } g ( z ) = w _ { 2 }$$

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

در این صورت می‌توان گزار‌ه‌های زیر را بیان کرد:

• $$\lim _ { z \rightarrow z _ { 0 } } f ( z ) + g ( z ) = w _ { 1 } + w _ { 2 }$$
• $$\lim _ { z \rightarrow z _ { 0 } } f ( z ) g ( z ) = w _ { 1 } \cdot w _ { 2 }$$
• اگر $$w _ { 2 } \neq 0$$ باشد در این صورت می‌توان گفت: $$w _ { 2 } \neq 0$$
• اگر $$h ( z )$$ تابعی پیوسته باشد که در همسایگی $$w _ 1$$ تعریف شده باشد، در این صورت می‌توان حد $$\lim _ { z \rightarrow z _ { 0 } } h ( f ( z ) ) = h \left( w _ { 1 } \right)$$ را بیان کرد.

البته در اینجا اثبات موارد فوق ارائه نشده است. توجه داشته باشید که حد تابع مختلط را می‌توان در قالب تابع دوضابطه‌ای نیز تعریف کرد. در این حالت حد بخش حقیقی و موهومی به طور مجزا بیان می‌شوند. در ادامه این حد ارائه شده است.

$$\lim _ { z \rightarrow z _ { 0 } } f ( z ) = w _ { 0 } \text { iff } \left \{ \begin {array} { l } { \lim _ { P \rightarrow P _ { 0 } } u ( x , y ) = u _ { 0 } } \\ { \lim _ { P \rightarrow P_{0}} v(x, y)=v_{0}}\end{array}\right.$$

مقادیر $$P$$ و $$P _ 0$$ و $$w _ 0$$ نیز برابرند با:

$$P = ( x , y ) , P _ { 0 } = \left ( x _ { 0 } , y _ { 0 } \right) , w _ { 0 } = u _ { 0 } + i v _ { 0 }$$

عبارت "iff" نشان‌دهنده گزاره اگر و تنها اگر است.

توابع پیوسته

یک تابع، در صورتی پیوسته است که هیچ بریدگی یا پرشی در آن وجود نداشته باشد. البته تعریف دقیق‌تر را می‌توان به صورت زیر بیان کرد:

تعریف: اگر تابع $$f ( z )$$ روی ناحیه‌ای باز در اطراف $$z _ 0$$ تعریف شده و حد $$\lim _ { z \rightarrow z _ { 0 } } f ( z ) = f \left( z _ { 0 } \right )$$ نیز موجود باشد، در این صورت می‌توان گفت تابع $$f ( z )$$ در نقطه $$z _ 0$$ پیوسته است.

حال فرض کنید که تابع مختلط به صورت مولفه‌های حقیقی و موهومیِ جداگانه بیان شود:

$$f ( z ) = u ( x , y ) + i v ( x , y )$$

اگر تابع مختلط به صورت بالا بیان شود در این صورت $$u ( x , y )$$ و $$v ( x , y )$$ باید به‌طور مجزا در نقطه مدنظر حد داشته باشند.

مثال ۴

تابعی چند‌جمله‌ای را به صورت زیر در نظر بگیرید.

$$P ( z ) = a _ { 0 } + a _ { 1 } z+ a _ { 2 } z ^ { 2 } + \ldots + a _ { n } z ^ { n }$$

این تابع روی تمامی صفحه مختلط، پیوسته است. دلیل این امر نیز آن است که $$( x + i y ) ^ { k }$$ روی تمامی صفحه پیوسته است.

ویژگی‌های توابع پیوسته

از آنجایی که پیوستگی بر حسب حد توضیح داده می‌شود، بنابراین می‌توان ویژگی‌های زیر را برای آن بیان کرد. بدین منظور در ابتدا فرض کنید $$f ( z )$$ و $$g ( z )$$ روی ناحیه‌ای همچون $$A$$ پیوسته باشد. در این صورت می‌توان گزاره‌های زیر را برای آن بیان کرد:

• $$f ( z )$$+$$g ( z )$$ روی تمامی ناحیه $$A$$ پیوسته است.
• حاصل ضرب $$f ( z )$$$$g ( z )$$ نیز روی ناحیه $$A$$ پیوسته است.
• $$f ( z ) / g ( z )$$ روی تمامی نواحی به جزء نواحی که در آن $$g ( z ) = 0$$، پیوسته است.
• اگر $$h$$ روی $$f ( A )$$ پیوسته باشد، در این صورت $$h ( f ( z ) )$$ نیز روی $$A$$ پیوسته است.

با استفاده از این ویژگی‌ها، می‌توان گفت توابعی به شکل زیر همواره پیوسته هستند.

• $$e ^ { z ^ 2 }$$
• $$\cos ( z ) = \left( \mathrm { e } ^ { i z } + \mathrm { e } ^ { - i z } \right) / 2$$

اگر $$P ( z )$$ و $$Q ( z )$$ چندجمله‌هایی پیوسته باشند، در این صورت کسر $$P ( z ) / Q ( z )$$ نیز در تمامی نقاط به جز ریشه‌های مخرج پیوسته خواهد بود.

حد بینهایت

زمانی مجموعه نقاط $$\{ z _ n \}$$ در بینهایت قرار دارند که اندازه آن‌ها به بینهایت میل کند ($$| z _ n | \to \infty$$). این میل کردن می‌تواند در هر جهتی باشد. توجه داشته باشید که با توجه به این تعریف، ممکن است بخش حقیقی یا موهومی یک عدد، بسیار کوچک باشد، اما اندازه آن بسیار زیاد و یا به عبارتی بینهایت باشد. در شکل زیر مسیر‌های مختلفی که در آن مقادیر $$z$$ به بینهایت میل می‌کنند، نشان داده شده‌اند.

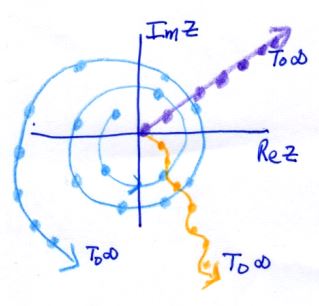
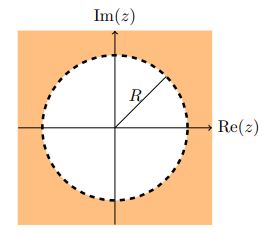
اگر یک دایره بزرگ به مرکز صفر ترسیم کنیم، در این صورت هرآنچه که در بیرون از این دایره قرار می‌گیرد را همسایگی بینهایت می‌نامند. در شکل زیر این همسایگی با رنگ نارنجی نشان داده شده است.

اگر حد زیر برقرار باشد،

$$\color {white} {\lim _ { z \rightarrow \infty } \frac { 1 } { z } = 0 } \lim _ { z \rightarrow \infty } \frac { 1 } { z } = 0 \color {white} {\lim _ { z \rightarrow \infty } \frac { 1 } { z } = 0 }$$

در این صورت می‌توان گزار‌ه‌های زیر را بیان کرد:

$$\begin {array} { l } {\lim _{ z \rightarrow z _ { 0 } } f ( z ) = \infty \Leftrightarrow \lim _ { z \rightarrow z _{ 0 } } 1 / f ( z ) = 0 } \\ \\ { \lim _ { z \rightarrow \infty } f ( z ) = w _ { 0 } \Leftrightarrow \lim _ { z \rightarrow 0 } f ( 1 / z ) = w _ { 0 } } \\ \\ { \lim _ { z \rightarrow \infty} f ( z ) = \infty \Leftrightarrow \lim _ { z \rightarrow 0 } \frac { 1 } { f ( 1 / z ) } = 0 } \end{array}$$

توجه داشته باشید که تعریف نشده و بینهایت، گزار‌ه‌هایی متفاوت در پاسخ حد محسوب می‌شوند.

مثال ۵

حاصل حد $$\lim _ { z \rightarrow \infty } e ^ { z }$$ در بینهایت موجود نیست. دلیل این امر این است که مقدار این تابع در بینهایت، در مسیر‌های مختلف متفاوت است. در حقیقت اگر این تابع به صورت $$\mathrm { e } ^ { z } = \mathrm { e } ^ { x } \mathrm { e } ^ { i y }$$ بیان شود، آن‌گاه می‌توان حاصل حد را از مسیر‌های مختلف بدست آورد. برای نمونه در ادامه، پاسخ این حد در دو مسیر متفاوت بدست آمده است.

$$\begin{array} { l } { \lim _ { x \rightarrow - \infty } \mathrm { e } ^ { x } \mathrm { e } ^ { i y } = 0 } \\ { \lim _ { x \rightarrow + \infty } \mathrm { e } ^ { x } \mathrm { e } ^ { i y } = \infty } \end {array}$$

همان‌طور که مشاهده می‌کنید از دو مسیر مختلف، دو پاسخ متفاوت بدست آمده، بنابراین این تابع در بینهایت حدی ندارد.

مشتق

تعریف مشتق یک تابع مختلط نیز مشابه با تابع حقیقی است. به طور دقیق‌تر می‌توان گفت مشتق تابعی مختلط همچون $$f ( z )$$ در نقطه $$z _ 0$$، با توجه به حد زیر تعریف می‌شود.

$$f ^ { \prime } \left( z _ { 0 } \right ) = \lim _ { z \rightarrow z _ { 0 } } \frac { f ( z ) -f \left( z _ { 0 } \right) } { z - z _ { 0 } }$$

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

اگر حد فوق موجود باشد، در این صورت به تابع $$f$$ در نقطه $$z _ 0$$ اصطلاحا تحلیلی یا مشتق‌پذیر گفته می‌شود. به همین صورت اگر $$f$$ روی ناحیه‌ای باز همچون $$A$$ مشتق‌پذیر باشد، در این صورت این تابع روی کل ناحیه $$A$$ تحلیلی تلقی می‌شود.

بدیهی است که محاسبه حد با استفاده از تعریف، کاری زمان‌بر و خسته‌کننده خواهد بود. از این رو بهتر است که در توابع مختلط نیز از قوانین مشتق‌گیری استفاده شود. اکثر قوانین مشتق‌گیری در توابع حقیقی را می‌توان برای توابع مختلط نیز بیان کرد. این قوانین به صورت زیر هستند.

• $$\frac { d } { d z } ( f ( z ) + g ( z ) ) = f ^ { \prime } + g ^ { \prime }$$
• $$\frac { d } { d z } ( f ( z ) g ( z ) ) = f ^ { \prime } g + f g ^ { \prime }$$
• $$\frac { d } { d z } ( f ( z ) / g ( z ) ) = \frac { f ^ { \prime } g - f g ^ { \prime } } { g ^ { 2 } }$$
• $$\frac { d } { d z } g ( f ( z ) ) = g ^ { \prime } ( f ( z ) ) f ^ { \prime } ( z )$$
• $$\frac { d f ^ { - 1 } ( z ) } { d z } = \frac { 1 } { f ^ { \prime } \left( f ^ { - 1 } ( z ) \right) }$$

برای درک روابط فوق، قانون ضرب در ادامه اثبات شده است.

$$\begin{aligned} \frac{d}{d z}(f(z) g(z)) &=\lim _{z \rightarrow z_{0}} \frac{f(z) g ( z ) - f \left(z_{0}\right) g\left( z _ { 0 } \right) } { z - z _ { 0 } } \\ &=\lim _{z \rightarrow z _ { 0 } } \frac{\left(f(z)-f \left( z _ { 0‌ } \right)\right) g ( z ) + f \left( z _ { 0 } \right) \left( g ( z ) - g \left( z _ { 0 } \right)\right)}{z-z _ { 0 } } \\ &=\lim _{z \rightarrow z _ { 0 } } \frac { f ( z ) - f \left( z _ { 0 } \right) } { z - z _ { 0 } } g ( z ) + f \left(z _ { 0 } \right) \frac{\left( g ( z ) - g \left( z _ { 0 } \right)\right ) } { z - z _ { 0 } } \\ & = f ^ { \prime } \left( z _ { 0 } \right) g \left( z _ { 0 } \right) + f \left( z _ { 0 } \right) g ^ { \prime } \left( z _ { 0 } \right) \end{aligned}$$

حال که با مفهوم حد و مشتق در توابع مختلط آشنا شدید در مطلب آینده تابع تحلیلی را توضیح خواهیم داد.

در صورتی که مطلب فوق برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضی
• مجموعه آموزش‌های فیزیک
• تابع مختلط — به زبان ساده
• تابع هارمونیک — به زبان ساده
• مانده تابع — به زبان ساده

^^