جمع و تفریق چند جمله ای ها — به زبان ساده

چند جملهای ها (Polynomial) در ریاضیات نقش بسیار مهمی دارند. بسیاری از توابع به صورت چند جمله ای نوشته میشوند. برای مثال توابع خطی، توابع سهمی و غیره همگی به صورت چند جملهای هستند. بنابراین جبر چند جملهای (انجام چهار عمل اصلی روی آنها) برای کسانی که در زمینه ریاضیات (حتی ریاضیات پایه) فعالیت دارند ضروری است. در دروس دبیرستان نیز جبر چند جمله ای ها یکی از بحثهای مهم تلقی میشود. در این نوشتار از مجله فرادرس به موضوع جمع و تفریق چند جمله ای ها خواهیم پرداخت و با ذکر مثالهای مختلف، زاویههای تاریک آن را برایتان روشن خواهیم کرد.
برای آشنایی بیشتر با چند جملهایها بهتر است نوشتارهای دیگر مجله فرادرس مانند چند جملهایها — به زبان ساده و تقسیم چند جمله ای ها — به زبان ساده را مطالعه کنید. همچنین خواندن کاربرد فاکتورگیری در حل معادلات ریاضی — به زبان ساده و اتحاد و تجزیه در ریاضی — به زبان ساده خالی از لطف نیست.
جمع و تفریق چند جمله ای ها
یک چند جملهای (Polynomial) به صورت عملگر جمع بین جملاتی از توانهای متغیر (که معمولا نامیده میشود) ساخته میشود. البته ممکن است بیش از یک متغیر نیز در چند جملهای نقش داده باشد که در این صورت چند جملهای را «چند متغیره» (Multivariate Polynomial) مینامیم. به چند جملهای زیر دقت کنید.
البته گاهی چنین چند جملهای را به صورت عبارتهای جبری نیز به کار میبرند.
برای پیدا کردن درجه چند جملهای چند متغیره ابتدا توانهای متغیرها را در هر یک از بخشها یا جملهها جمع کرده و بزرگترین آنها را به عنوان «درجه چند جملهای» (Degree of Polynomial) به کار میبریم. برای مثال در چند جملهای قبلی، درجه یا مرتبه، برابر با ۵ است زیرا بزرگترین مجموع توانها مربوط به جمله است.
ولی زمانی که چند جملهای فقط از یک متغیر تشکیل شده باشد، آن را یک چند جملهای «تک متغیره» (Univariate Polynomial) نامگذاری کردهاند. در این حالت بزرگترین توان متغیر، درجه چند جملهای را مشخص میکند. معمولا برای نمایش چند جملهایها از حروف بزرگ لاتین مثل یا استفاده میکنند و درجه آن را به صورت اندیس در پایین این حروف نمایش میدهند. به این ترتیب ، یک چند جملهای از درجه ۴ است که متغیر آن محسوب شده است. فرم کلی چند جملهای تک متغیره درجه به صورت زیر نوشته میشود. به علامت جمع () که برای نمایش عملیات جمع به صورت خلاصه در رابطه قرار گرفته، توجه کنید.
رابطه بالا به شرطی که باشد، یک چند جملهای مرتبه یا درجه است. درجه چند جملهای باید یک عدد صحیح و نامنفی باشد. در ادامه این متن هر زمان به چند جملهایها اشاره میکنیم، منظورمان چند جملهای تک یا یک متغیره است.
نکته: همانطور که گفته شد، توان هر یک از متغیرها در چند جملهای، نمیتواند منفی یا کسری باشد. البته وجود ضرایب غیر صحیح (مثل ) در چند جملهایها مشکلی ایجاد نمیکند. اگر توانها غیر صحیح و منفی باشند، در این حالت، ترکیب چنین جملههایی را یک «عبارت جبری» (Algebra Expression) مینامند.
در زیر یک نمونه از چند جملهای درجه ۴ را مشاهده میکنید.
البته ممکن است بعضی از ضرایب جملهها صفر باشند. در این صورت چند جملهای را ناقص میگویند. برای مثال چند جملهای زیر از درجه ۴ بوده ولی ناقص محسوب میشود، زیرا ضرایب متغیر برای توانهای ۲ و ۳ برابر با صفر است.
باید توجه داشته باشید که جمع یا تفریق چند جمله ای ها باز هم باعث تولید یک چند جملهای میشود.
نکته: توابع چند جملهای، هموار و پیوسته هستند. این گونه خصوصیات، چنین توابعی را پرکاربرد کرده و اغلب در ریاضیات و علوم دیگر، برای تقریب توابع پیچیده از توابع چند جملهای استفاده میکنند.
در ادامه در سه بخش به مفهوم و شیوه محاسبه جمع و تفریق چند جمله ای ها خواهیم پرداخت. ابتدا نقش جمله یا جملههای مشابه را در جمع و تفریق چند جمله ای ها بیان کرده، سپس عمل جمع و تفریق چند جمله ای را با ذکر مثال بازگو خواهیم کرد.
جمله مشابه بین چند جمله ای ها
جمله مشابه در بین دو چند جملهای، عبارتی است که توان متغیر یا متغیرهای آن در هر دو چند جملهای یکسان باشد. توجه داشته باشید که در اینجا مشابه به معنی داشتن توان یکسان در هر دو عبارت است و ضرایب در تعیین این عبارت مشابه نقشی ندارند. برای مثال در سطرهای زیر عبارتهای مشابه بین دو چند جملهای مشخص شدهاند.
برای جمع و تفریق چند جملهای ها، شناخت جملات مشابه از اهمیت زیادی برخودار است. همین موضوع را در محاسبات مربوط به عبارتهای جبری نیز باید مد نظر قرار دهید.
نکته: اگر هم توان و هم ضریب متغیر در چند جملهای، یکسان بود، هر دو عبارت با هم برابر هستند.
جمع چند جمله ای ها
برای آشنایی با نحوه جمع کردن چند جملهایها به ذکر دو مثال میپردازیم. به یاد داشته باشید که کلید اصلی در این محاسبه، شناسایی جملههای مشابه است.
مثال ۱
حاصل جمع چند جملهایهایی که در ادامه مشاهده میکنید براساس جمع جبری ضرایب جملههای مشابه نوشته شده است.
نتیجه حاصل از جمع دیگر هیچ جمله مشابهای ندارد، در نتیجه عبارت مورد نظر، از این حالت سادهتر نخواهد شد.
مثال ۲
در این مثال، جملههای مشابه به تعداد همه جملهها نیست. به همین دلیل شاید کار محاسبه سادهتر شده باشد.
مشخص است که جملههای غیر مشابه، در جمع ظاهر شده و بدون تغییر باقی مانده و در نتیجه حاصل جمع ظاهر میشوند. در ادامه نیز ضریب جملههای مشابه را از طریق جمع جبری محاسبه کرده و به همراه متغیرشان نمایش دادهایم تا حاصل جمع تکمیل گردد.
نکته: گاهی برای شناسایی بهتر جملههای مشابه، هر دو چند جملهای را براساس درجه جملهها، به ترتیب قرار داده و به صورت جمع زیر هم، محاسبات را دنبال میکنند. در تصویر زیر نمونهای از این حالت را مشاهده میکنید.
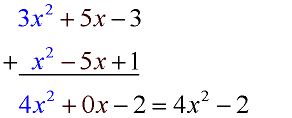
تفریق چند جمله ای ها
فرض کنید قرار است چند جملهای را از کم کنیم. باز هم از الگوی اعداد برای مشخص کردن نحوه تفریق چند جملهایها استفاده میکنیم. کافی است عبارت را قرینه کنیم و با جمع کنیم. به یاد دارید که تفریق عدد ۱۵ از ۲۸ را به صورت زیر مینویسیم:
به همین ترتیب برای تفاضل دو چند جملهای نیز به صورت زیر عمل میکنیم.
نکته: قرینه یک چند جمله ای به سادگی قابل محاسبه است. کافی است در تمامی جملهها، علامتهای جمع را به تفریق و تفریق را به جمع تبدیل کنید. یا کل چند جملهای را در ضرب کنید. مطلبی در مورد ضرب چند جملهایها نیز در مجله فرادرس منتشر شده است.
برای روشن شدن موضوع به دو مثال میپردازیم که مربوط به جمع و تفریق چند جمله ای ها است.
مثال ۳
حاصل تفریق چند جملهای های زیر را بوسیله قرینه سازی و جمع انجام میدهیم.
مثال ۴
با توجه به این که درجه دو چند جملهای ها برای محاسبه تفاضل یکسان نیست، جملات غیر مشابه در تفریق باقی میمانند.
توجه داشته باشید که عبارت با ضریب صفر در چند جملهای نوشته نمیشود.
نکته: از آنجایی که عملگر جمع دارای خاصیت جابجایی است، میتوانیم ترتیب جملهها را از درجه بزرگتر به کوچکتر بنویسیم. البته این امر الزامی نیست ولی خواندن چند جملهای در این حالت سادهتر خواهد شد.
همانطور که در تصویر زیر میبینید، مرتبسازی براساس درجه هر عبارت در سادهسازی جمع و تفریق چند جمله ای ها بسیار موثر است. به این ترتیب جملههای مشابه در زیر یک دیگر نوشته شده و جمع جبری صورت میگیرد. واضح است که ضریب جمله های ناموجود برای هر توان، صفر در نظر گرفته میشود. به همین دلیل ضریب در چند جملهای اول صفر قرار گرفته است تا به این ترتیب همه جملههای مشابه (به ترتیب توان) در زیر یکدیگر نوشته شوند.
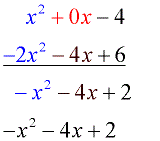
خلاصه و جمعبندی
همانطور که در این متن از مجله فرادرس خواندید، موضوع جمع و تفریق چند جمله ای ها بسیار ساده است ولی در اغلب موارد دانش آموزان مقطع دبیرستان با شنیدن عبارت چند جملهای سردرگم میشوند. در این نوشتار سعی کردیم که پیچیدگی مفهومی برای جبر چند جملهای ها بخصوص جمع و تفریق را کاهش دهیم. به این ترتیب با ذکر مثال های مختلف و متنوع انتظار داریم همه موضوعات در حوزه جمع و تفریق چند جمله ای ها را پوشش داده باشیم. در نوشتارهای دیگر از مجله فرادرس، به موضوع ضرب و تقسیم چند جملهایها نیز پرداخته شده است.













سلام وقت شما به خیر. ممنون از شما.
اگر دو موغیر داشته باشیم چه باید کرد؟
مثلا دوجمله ای:
چطور 18b به توان دو را از 12a به توان دو کسر کنیم؟
سلام.
در این صورت یک چندجملهای بهصورت زیر داریم که −(18b)2 و (12a)2 جملات آن هستند:
(12a)2−(18b)2=144a2−324b2
موفق باشید.
در مثال ۲ به جای x- نوشته شده 4x-
در مثال ۳ به جای ۲+ نوشته شده ۲-
درود بیکران!
از اینکه اشکالات و اشتباهات ما را گوشزد میکنید، سپاسگزاریم. متن مطابق با نظر شما تغییر و دوباره منتشر شد. از همراهی شما فرهیخته گرامی، با مجله فرادرس، خرسندیم.
پیروز و سربلند باشید.