تقسیم چند جمله ای ها — به زبان ساده

حتما تا به حال با مفهوم «چند جملهای» (Polynomial) در دیگر نوشتههای فرادرس آشنا شدهاید. در این قسمت به تقسیم چند جمله ای ها و شیوه محاسبه آن میپردازیم. برای شروع بهتر است مفهوم تقسیم و ویژگیهای آن را مرور کنیم.
فرض کنید قرار است هفت شیرینی را بین دو نفر تقسیم کنیم. حاصل چه خواهد بود.
به این معنی که خارج قسمت این تقسیم برابر با ۳ و باقیمانده آن نیز برابر با 0.5 یا همان است.
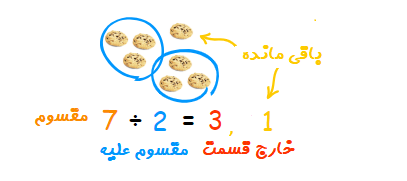
در اینجا را «مقسوم» (Dividend)، را «مقسوم علیه» (Divisor) و را «خارج قسمت» (Quotient) مینامند. همچنین مقدار «باقیمانده» (Reminder) تقسیم خوانده میشود.
به این ترتیب مشخص است که میتوان حاصل این تقسیم را به صورت زیر نیز نمایش داد.
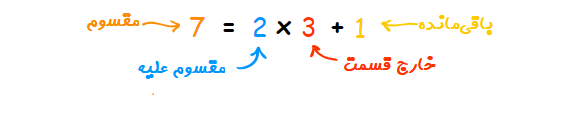
این تصویر نشان میدهد که میتوان مقسوم را به صورت حاصلضرب مقسوم علیه در خارج قسمت بعلاوه باقیمانده نوشت. در ادامه، از همین خصوصیات و قواعد برای تقسیم چندجملهایها نیز استفاده خواهیم کرد.
تقسیم چند جمله ای
برای آشنایی با نحوه تقسیم چند جمله ای ها، بهتر است برای یادآوری، به مفهوم و خصوصیات چندجملهایها اشارهای کوتاه داشته باشیم ولی برای آشنایی بیشتر با آنها بهتر است مطلب چندجملهایها – به زبان ساده را مطالعه کنید.
چند جملهایها
همانطور که به یاد دارید شکل استاندارد یک چند جملهای درجه n به صورت زیر است:
از آنجایی که بزرگترین توان در این چند جملهای n است، آن را چند جملهای درجه n مینامند. مشخص است که در این حالت ضریب متغیر و نیز ضریب متغیر است. همینطور ضریب متغیر و ضریب متغیر است. در انتها نیز ضریب متغیر محسوب شده ولی به علت آنکه هر مقدار به توان ۰ برابر با ۱ است، این جمله فقط با ضریب نمایش داده شده است. در حقیقت چند جملهای درجه n باید به صورت زیر نوشته میشد:

ولی برای سادگی و راحتی کار چندجملهای درجه را به شکلی که قبلا دیدید، نمایش میدهیم. به این ترتیب یک چند جملهای درجه n را کامل مینامیم، اگر همه جملات آن وجود داشته باشد. از طرفی نماد به ما میگوید که با یک چند جملهای کامل درجه n سروکار داریم که متغیر آن x است.
اگر چند جملهای کامل نباشد (همه جملات آن موجود نباشد) آن را چند جملهای ناقص مینامیم. مشخص است که چند جملهای درجه n، باید حتما دارای عبارت باشد به این معنی که ضریب است. برای مثال چند جملهای یک چند جملهای کامل است در حالیکه چند جملهای ناقص درجه ۳ نامیده میشود. ولی دیگر یک چند جملهای درجه ۳ ناقص نخواهد بود، زیرا بزرگترین توان آن دیگر ۳ نیست.
مفهوم تقسیم چندجملهایها
فرض کنید چند جملهای را میخواهیم بر تقسیم کنیم. یعنی داشته باشیم:
که در آن مقسوم، مقسوم علیه، خارج قسمت و نیز باقیمانده نامیده میشود. در نتیجه خواهیم داشت.
به تفاوت درجههای چند جملهایها دقت کنید. برای آنکه این تقسیم امکان پذیر باشد، باید باشد. همچنین همیشه و است. بنابراین برای مثال، اگر یک چند جملهای درجه ۵ را بر یک چند جملهای درجه ۲ تقسیم کنیم، خارج قسمت یک چند جملهای درجه ۳ خواهد بود. همینطور باقیمانده نیز یک چند جملهای درجه ۱ بدست میآید.
که در این صورت داریم:
نکته: ممکن است در حالت کلی بعضی از این چندجملهایها، مثل مقسوم، مقسوم علیه، خارج قسمت و یا باقیمانده، چندجملهای کامل نباشند.
تقسیم چند جمله ای به روش فاکتورگیری
گاهی برای انجام تقسیم دو چندجملهای میتوان از روش فاکتورگیری استفاده کرد و عملیات تقسیم را به سرعت و سادگی انجام داد. در این حالت معمولا تقسیم را به صورت کسر نشان داده و عوامل مشترک را در صورت و مخرج کسر مشخص و ساده میکنند. حاصل کسر ساده شده خارج قسمت را نشان میدهد.

مثال ۱
فرض کنید باید تقسیم چند جمله ای را بر محاسبه کنیم. ابتدا تقسیم را به صورت کسر مینویسیم و عوامل مشترک (فاکتور) صورت و مخرج را مشخص میکنیم.
با حذف عوامل مشترک در صورت و مخرج، کسر را ساده میکنیم.
به این ترتیب خارج قسمت برابر با و باقیمانده نیز برابر با صفر است، زیرا:
مثال ۲
خارج قسمت و باقیمانده تقسیم چندجملهای را بر به صورت زیر محاسبه میکنیم.
مشخص است که اینجا از اتحاد جمله مشترک استفاده کردهایم. با حذف عوامل مشترک در صورت و مخرج، کسر را ساده میکنیم.
به این ترتیب خارج قسمت برابر با و باقیمانده نیز برابر با صفر است، زیرا:
مثال ۳
فرض کنید باید تقسیم چند جمله ای را بر محاسبه کنیم. باز هم تقسیم را به صورت کسر مینویسیم.
پس از ساده کردن کسرها خواهیم داشت:
در نتیجه خارج قسمت برابر با و باقیمانده نیز صفر خواهد بود، زیرا:
تقسیم چندجملهای بدون فاکتورگیری (روش طولانی)
برای انجام تقسیم چندجملهای بر چندجملهای طبق قواعد تقسیم اعداد عمل میکنیم. در این روش براساس مراحل زیر، عمل تقسیم را انجام میدهیم.
- ابتدا جملات چندجملهای مقسوم را براساس بزرگترین توانها از چپ به راست مرتب میکنیم. به این ترتیب جمله با بزرگترین توان در سمت چپ قرار میگیرد.
- عمل مرتبسازی جملات چندجملهای مقسوم علیه را نیز برحسب توانهای بزرگ به کوچک انجام میدهیم.
- اولین جمله از سمت چپ چندجملهای مقسوم را بر اولین جمله از سمت چپ مقسوم علیه تقسیم میکنیم.
- باقیمانده تقسیم مرحله ۳ را بر مقسوم علیه محاسبه میکنیم و خارج قسمت حاصل را با خارج قسمت مرحلههای قبلی جمع میکنیم.
- عمل تقسیم را تا زمانی که درجه چند جملهای باقیمانده از درجه مقسوم علیه کمتر شود، ادامه میدهیم.
نکته: برای محاسبه باقیمانده در هر مرحله، راحتتر است که عبارت اول را با قرینه عبارت دوم جمع کنید.
مثال 4
حاصل تقسیم چندجملهای را بر محاسبه کنید.
مشخص است که جملات چندجملهای مقسوم و مقسوم علیه به ترتیب توانهای بزرگ به کوچک قرار گرفتهاند. پس کافی است تقسیم جملههای دارای توانهای بزرگتر را آغاز کنیم. یعنی خواهیم داشت که خارج قسمت این تقسیم برابر با است. سپس نتیجه تقسیم (خارج قسمت) را در مقسوم علیه ضرب کرده و در زیر چند جملهای مقسوم قرار میدهیم.
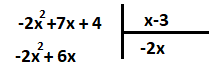
در مرحله بعدی، حاصل ضرب ایجاد شده را از مقسوم کم میکنیم و باقیمانده را بدست میآوریم.
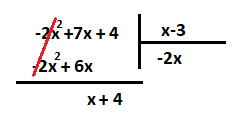
عمل تقسیم باقیمانده بر مقسوم علیه، را در این مرحله انجام داده و خارج قسمت را به خارج قسمت مرحله قبل اضافه میکنیم.
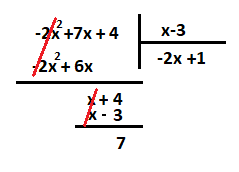
از آنجایی که درجه x در باقیمانده (که در اینجا صفر است) از درجه مقسوم علیه کمتر شده است، عمل تقسیم ادامه نخواهد یافت. در نتیجه خارج قسمت برابر با و باقیمانده نیز است. زیرا:
نکته: در مواقعی که باقیمانده صفر نیست، میتوان خارج قسمت و باقیمانده را ترکیب کرد و به صورت کلی، خارج قسمت را به شکل زیر نوشت:
مشخص است که در این حالت، باقیمانده باید برمبنای مقسومعلیه نوشته شود، یعنی دارای مخرجی برابر با مقسوم علیه باشد. این شیوه نمایش خارج قسمت، به همان شکلی است که در ابتدای متن برای تقسیم کردن اعداد به آن اشاره کردیم و برای مثال حاصل تقسیم بر یعنی را به صورت نوشتیم.
مثال 5
حاصل تقسیم عبارت بر را بدست میآوریم. مشخص است که چند جملهای مقسوم مرتب نیست. ابتدا جملات این چندجملهای را به ترتیب از بزرگ به کوچک مرتب میکنیم.
نکته: از آنجایی که ممکن است در طی مراحل تقسیم به جملات با توانهایی برخورد کنیم که در باقیمانده وجود نداشته باشد، بهتر است مقسوم را به صورت چندجملهای کامل بنویسیم. بنابراین مقسوم به صورت زیر در خواهد آمد.
حال مراحل تقسیم را آغاز میکنیم.
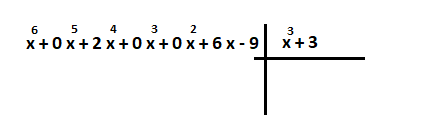
مشخص است که نسبت جملات با بزرگترین توانها در مقسوم و مقسوم علیه به صورت خواهد بود.
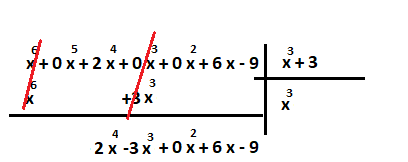
حال براساس باقیمانده عمل تقسیم بر مقسوم علیه را ادامه میدهیم.
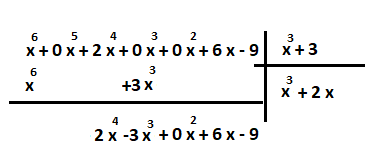
اکنون خارج قسمت را در مقسوم علیه ضرب کرده و باقیمانده تقسیم را بدست میآوریم.
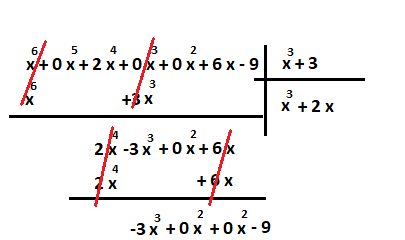
و در آخرین مرحله نیز عمل تقسیم را ادامه داده تا به باقیماندهای برسیم که جمله با بزرگترین توان آن از ۳ یعنی بزرگترین توان مقسوم علیه، کمتر باشد.
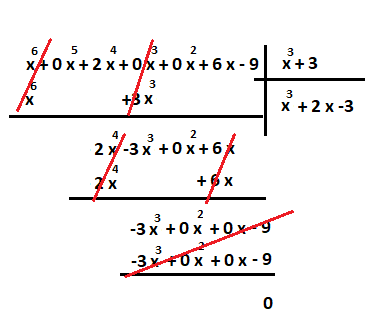
به این ترتیب عمل تقسیم پایان یافته و باقیمانده نیز صفر است. بنابراین میتوان برای آزمایش صحت عملیات تقسیم به صورت زیر عمل کرد:













سلام
جوابتون اشتباهه
6x+7x میشه 13x نه x منها که نیس جمعه
با سلام و وقت بخیر؛
در مرحله دوم، حاصل ضرب ایجاد شده را از مقسوم کم کردیم. در واقع، عملیات زیر را در مرحله دوم انجام دادیم.
–2x2+7x+4–(–2x2+6x)
–2x2+7x+4+2x2–6x
7x+4–6x
x+4
به همین خاطر، علامت جملهها، قرینه شد و x+4 در باقیمانده قرار گرفت.
از همراهی شما با مجله فرادرس سپاسگزاریم.
عالی بود
ممنون
عالی بود.
عالی بود. خیلی ممنون??
good job
سلام و خدا قوت – عالی عالی ممنون