توان در مدار سه فاز — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزشهای پیشین مجله فرادرس، مفاهیم مدارهای سهفاز و روابط حاکم بر آنها را بیان کردیم. در این آموزش، توان در مدار سه فاز و نحوه محاسبه آن را بررسی خواهیم کرد.
برای بهدست آوردن توان در یک سیستم سهفاز، ابتدا توان یک فاز را محاسبه، سپس آن را در سه ضرب میکنیم. برای این کار میتوان از کمیتهای پریونیت نیز استفاده کرد. از آنجایی که فقط اندازه کمیتها در بسیاری از فرمولها و محاسبات توان وجود دارد، و از آنجایی که اندازههای مربوط به سهفاز برابر است، میتوان از یک عبارت ساده برای بهدست آوردن توان استفاده کرد. در ادامه، از $$V_ \phi$$ برای نمایش اندازه ولتاژ فاز، $$I_ \phi$$ برای اندازه جریان فاز و $$V_L$$ و $$I_L$$ بهترتیب، برای ولتاژ و جریان خط استفاده میکنیم. همچنین، $$\mathrm{Z}_\phi$$ را برای اندازه امپدانس فاز بهکار میبریم.
توان اکتیو بار ستاره متعادل
بار ستاره شکل ۱ را در نظر بگیرید. توان هریک از فازها در بخش (ب) این شکل نشان داده شده و برابر با حاصلضرب اندازه ولتاژ فاز $$V_ \phi$$ و جریان فاز $$I_ \phi$$ و کسینوس زاویه $$\theta _\phi$$ بین آنها است.
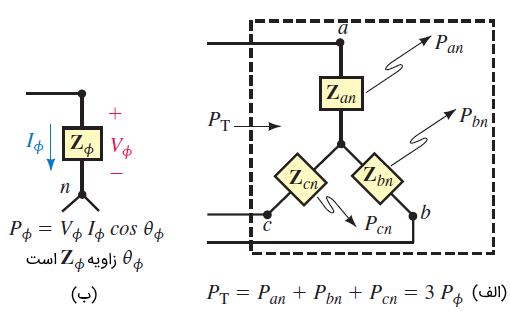
از آنجایی که زاویه بین ولتاژ و جریان فاز، همواره برابر با زاویه امپدانس بار است، توان هر فاز بهصورت زیر تعریف میشود:
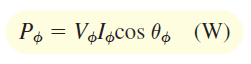
که در آن، $$\theta _ \phi$$ زاویه امپدانس $$\mathbf{Z}_ \phi $$ است. توان کل نیز برابر است با:
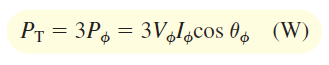
فرمول اخیر را میتوان برحسب کمیتهای خط نیز بیان کرد. همانطور که میدانیم، برای یک بار ستاره، $$I_\phi = I_L$$ و $$V_ \phi =V_L /\sqrt{3}$$ است که در آنها، $$I_L$$ و $$V_L$$ بهترتیب، اندازه جریان و ولتاژ خط هستند. با جایگذاری این روابط در رابطه (۲)، و دانستن اینکه $$3/\sqrt{3}= \sqrt{3}$$، داریم:
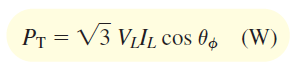
رابطه فوق، فرمول مهمی است که بسیار مورد استفاده قرار میگیرد. دقت کنید که $$\theta _ \phi$$ زاویه امپدانس بار است و زاویه بین $$V_L$$ و $$I_L$$ نیست.
توان هر فاز را میتوان بهصورت زیر نیز بیان کرد:
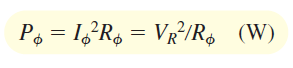
که در آن، $$R_\phi$$ مؤلفه مقاومتی امپدانس فاز، و $$V_R$$ ولتاژ دو سر آن است. توان کل سه فاز برابر است با:
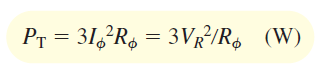
توان راکتیو بار ستاره متعادل
مشابه توان اکتیو، فرمولهای توان راکتیو را میتوان بهصورت زیر نوشت:
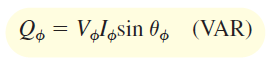
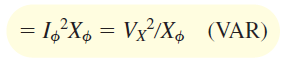
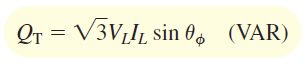
که در آنها $$X_ \phi$$ مؤلفه راکتیو $$\mathbf{Z}_\phi$$، و $$V_X$$ ولتاژ دو سر آن است.
توان ظاهری
توان ظاهری، بهصورت زیر تعریف میشود:
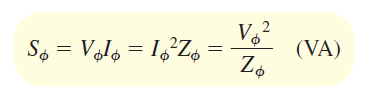
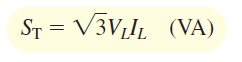
ضریب توان
ضریب توان، نسبت توان اکتیو به توان ظاهری است:
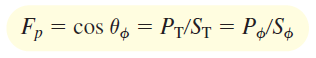
توان بار مثلث متعادل
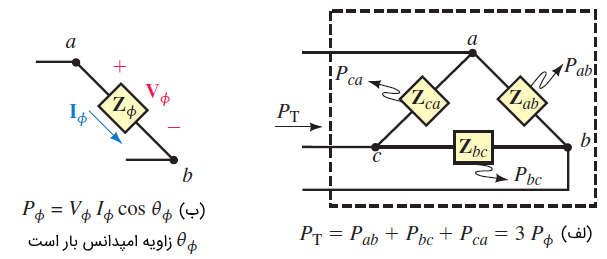
برای یک بار مثلث (شکل ۲ (الف))، توان هر فاز، بهصورت زیر تعریف میشود:
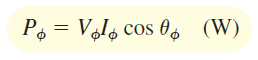
که در آن، $$\theta _\phi$$ زاویه امپدانس بار مثلث است. همانطور که میبینیم، این فرمول مشابه رابطه (۱) مربوط به بار ستاره است. برای توان راکتیو و ضریب توان نیز این شباهت وجود دارد.
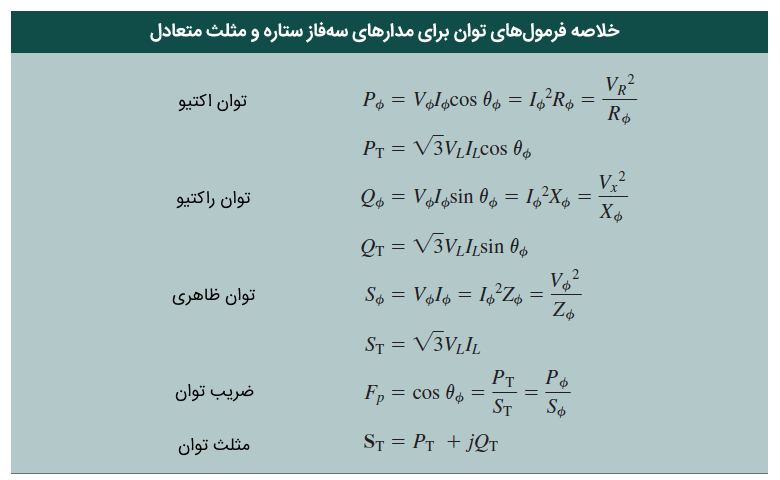
در جدول زیر، فرمولهای مربوط به توان برای بارهای ستاره و مثلث آورده شده است. در همه فرمولهای این جدول، $$\theta _ \phi$$ زاویه امپدانس بار است ($$\mathbf{Z}_{an}$$ برای بارهای ستاره و $$\mathbf{Z}_{ab}$$ برای بارهای مثلث).
توجه کنید که برای محاسبات توان، از مدار معادل تکفاز نیز میتوانیم استفاده کنیم.
اندازهگیری توان در مدارهای سهفاز
برای اندازه گیری توان در یک سیستم سهفاز، بسته به اینکه سهسیمه یا چهارسیمه باشد، باید از چند واتمتر استفاده کرد.
برای یک سیستم چهارسیمه به سه واتمتر نیاز داریم، در حالی که در یک سیستم سهسیمه دو واتمتر کافی است.
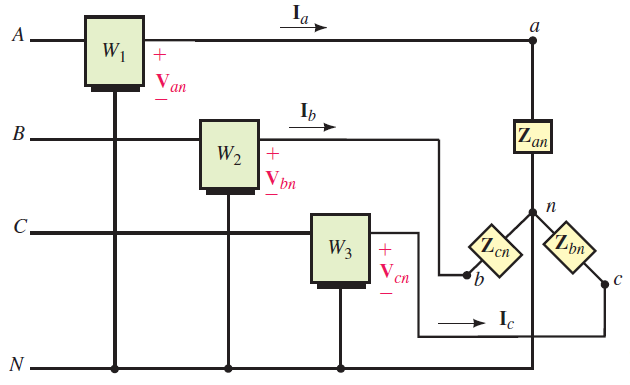
ابتدا سیستم چهارسیمه شکل ۳ را در نظر بگیرید. برای اندازهگیری توان این مدار، توان هریک از فازها را با یک واتمتر اندازهگیری میکنیم. برای این کار، هر واتمتر را بهگونهای متصل میکنیم که جریان فاز از سیمپیچ آن بگذرد و ولتاژ آن، همان ولتاژ فاز باشد. برای مثال، ولتاژ واتمتر $$W_1$$ برابر $$V_{an}$$ و جریان آن برابر $$I_a$$ است. بنابراین، نتیجهای را که از واتمتر میخوانیم، برابر است با:
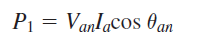
که همان توان فاز $$an$$ است. بهطریق مشابه، $$W_2$$ توان فاز $$bn$$ و $$W_3$$ توان فاز $$cn$$ را نشان میدهد. توان کل، برابر است با:
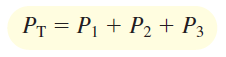
روند فوق، برای مدارهایی با بار نامتعادل نیز برقرار است.
برای اندازهگیری توان در یک سیستم سهسیمه، دو واتمتر کافی است. اتصال واتمترها در شکل ۴ نشان داده شده است. بارها میتوانند ستاره یا مثلث، متعادل یا نامتعادل باشند.
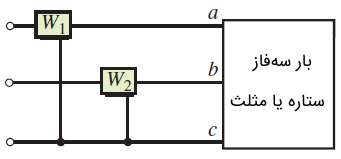
همانطور که در شکل بالا نشان داده شده است، میتوان دو سر واتمترها را به دو ترمینال ولتاژ خط و سر دیگر آن را به ترمینال ولتاژ خط سوم متصل کرد. در نتیجه، توان کل بار، برابر با جمع جبری مقادیری است که واتمترها نشان میدهند. این روش، روش دو واتمتر نامیده میشود. عددی که هر واتمتر نشان میدهد برابر با حاصلضرب اندازه ولتاژ، جریان و کسینوس زاویه بین آن دو است.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
^^











سلام ،وقتی برای مثال می گوییم توان این الکتروموتور5kwهست درحالت مثلث هست یا ستاره؟
ممنون
آموزش ها بسیار عالی و کاربردی هستند و با سپاس از جناب امید زندی که بسیار مسلط و عالی مطالب تشریح و توضیح می دهند، رشته ام برق نیست اما به موضاعات برقی خیلی علاقه مندم
سلام
من ازروی جریان و ولتاژ یه شناور که داخل چاه هستش چطور میتونم محاسبه کیلو وات شناور رو انجام بدم راهنمایی کنید ممنون
سلام.
میتوانید از رابطه (۳) این آموزش استفاده کنید.
سالم و موفق باشید.
فرق بین کنتور دیجیتال سه فاز (۱۰۰)۵ آمپر با کنتور دیجیتال سه فاز (۱۰۰)۲۰ آمپر در چیست؟ تشکر
با سلام لااقل چند مثال از هر فرمول بزنید
بسیار عالی و اموزنده
بسیار جامع و در دسترس
درود سپاس از زحمات شما