فرادرس
مدولاسیون OFDM یا تقسیم فرکانسی چندگانه متعامد چیست؟ — از صفر تا صد
«تقسیم فرکانسی چندگانه متعامد» (Orthogonal Frequency Division Multiplexing) یا مدولاسیون OFDM یکی از روش‌های مدولاسیون است که دارای مزیت‌های بسیاری در انتقال داده‌های دیجیتال است. تکنیک مدولاسیون تقسیم فرکانسی چندگانه متعامد در برخی از جدیدترین سیستم‌های وایرلس پهن باند با نرخ داده بالا مانند WIFI و مخابرات از راه دور سلولی مورد استفاده قرار می‌گیرد. در این مطلب قصد داریم به بررسی اصول کار این روش مدولاسیون بپردازیم و ویژگی‌های آن را بیان کنیم.
مدولاسیون تقسیم فرکانسی چندگانه متعامد یا OFDM
مدولاسیون تقسیم فرکانسی چندگانه متعامد یا OFDM از تعداد زیادی سیگنال‌های حامل استفاده می‌کند که هر کدام از این سیگنال‌های حامل مسئول حمل داده‌های با نرخ بیت پایین هستند. این امر بدین معنی خواهد بود که مدولاسیون OFDM در مقابل «محوشدگی گزینشی» (Selective Fading)، تداخل و اثرات چند مسیری بسیار منعطف است و همچنین درجه کارایی طیفی بالایی دارد. برای سیستم‌های اولیه که از روش مدولاسیون OFDM استفاده می‌کردند، پردازش‌های مورد نیاز در این روش نسبتا سنگین بود. اما با پیشرفت تکنولوژی، مشکلات مدولاسیون OFDM در زمینه توان پردازش مورد نیاز تا حد بسیار زیادی کاهش یافت.
تاریخچه مدولاسیون OFDM
استفاده از روش مدولاسیون OFDM و مدولاسیون چند حاملی به سال‌های اخیر باز می‌گردد. استفاده از این مدولاسیون پلتفرم بسیار مناسبی را برای مخابرات بی‌سیم داده‌‌ها فراهم کرده است. مدولاسیون OFDM اولین بار در سال‌های ۱۹۶۰ و ۱۹۷۰ و در طول تحقیقات روی روش‌های کاهش اثر تداخل بین کانال‌های نزدیک به هم بررسی شد. در واقع هدف از این تحقیقات، نیاز به یک روش مدولاسیون بود که تا حد ممکن مخابرات داده بدون خطا در حضور تداخل و شرایط انتشار گزینشی محقق شود. برای استفاده از روش مدولاسیون OFDM به سطح نسبتا بالایی از پردازش نیاز بود که در آن زمان و در کاربردهای متداول چنین امکانی وجود نداشت.
برخی از اولین سیستم‌هایی که توانستند از روش مدولاسیون تقسیم فرکانسی چندگانه متعامد استفاده کنند، سیستم‌های پخش تلویزیونی دیجیتال بودند. در این سیستم‌ها، مدولاسیون OFDM قادر بود انتقال داده با قابلیت اطمینان بسیار بالا را در شرایط و مسیرهای سیگنال مختلف امکان پذیر کند. یک مثال از این سیستم‌ها در رادیو دیجیتال DAB بود که در اروپا مورد استفاده قرار می‌گرفت. یک کمپانی در کشور نروژ اولین بار اقدام به استفاده از مدولاسیون OFDM برای پخش تلویزیونی کرد.
در سال‌های بعد، به دلیل افزایش توان پردازش سیستم‌ها و نیز افزایش سطح تجمیع مدارات، مهندسان توانستند از روش OFDM در سیستم‌های مخابرات موبایل 4G نیز استفاده کنند و این سرویس از سال ۲۰۰۹ مورد استفاده وسیع قرار گرفت. همچنین امروزه از مدولاسیون OFDM برای WIFI و گستره وسیعی از سایر سیستم‌های داده وایرلس استفاده می‌شود.
اصول کار مدولاسیون OFDM
همان طور که گفتیم، مدولاسیون تقسیم فرکانسی چندگانه متعامد یکی از روش‌های مدولاسیون چند حاملی به شمار می‌آید. یک سیگنال OFDM از تعدادی سیگنال حامل مدوله شده نزدیک به هم تشکیل شده است.
در تصویر زیر نمایی از سیگنال‌های حامل چندگانه در مدولاسیون OFDM نشان داده شده است.
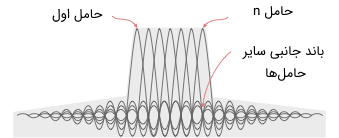
زمانی که مدولاسیونی از هر نوع (صوت، تصویر، داده و ...) را به یک سیگنال حامل اعمال کنیم، آن‌گاه باندهای جانبی از هر طرف گسترده می‌شوند. برای یک گیرنده امری بسیار ضروری است که بتواند تمام سیگنال را به صورت کامل دریافت کند تا در نهایت سیگنال پیام اصلی را از طریق دمدولاسیون سیگنال دریافتی بازسازی کند. در نتیجه، زمانی که سیگنال‌ها بسیار نزدیک به یکدیگر ارسال می‌شوند، باید مدولاسیون به صورتی باشد که گیرنده با استفاده از یک فیلتر قادر به تفکیک آن‌ها از یکدیگر باشد. برای این کار می‌توان از یک باند محافظتی بین هر کدام از آن‌ها استفاده کرد. اگرچه باندهای جانبی از هر حامل با یکدیگر همپوشانی دارند، اما باز هم می‌توان آن‌ها را بدون تداخل (که ممکن است انتظار آن را داشته باشیم.) دریافت کرد؛ زیرا این سیگنال‌ها بر یکدیگر عمود هستند. در ادامه قصد داریم به بررسی اصول کار مدولاسیون تقسیم فرکانس چندگانه متعامد بپردازیم و تمام این موارد را به صورت واضح‌تر بیان کنیم.
در مخابرات اگر انتقال یک سیگنال دیجیتال را در درون یک کانال غیر ایده‌آل در نظر بگیریم، مشاهده می‌کنیم که زمانی که «هم‌پاسخی سرعت سیستم» (reciprocal of the system rate) تا حد زیادی کوچک‌تر از «انتشار زمانی» (طول پاسخ ضربه) کانال غیر ایده‌آل باشد، این کانال موجب ایجاد «تداخلات بین سمبلی» (Intersymbol Interference) می‌شود. در چنین حالتی، یک برابر کننده یا اکوالایزر کانال در گیرنده اعمال می‌شود تا اعوجاجات کانال را جبران کند.
اگر کانال از نوع میان گذر با پهنای باند مشخص باشد، آن‌گاه سیگنال شامل اطلاعات ممکن است در باند پایه تولید شود و سپس به فرکانس باند عبور انتقال یابد. بنابراین سیگنال شامل اطلاعات روی یک سیگنال حامل تکی منتقل می‌شود. نکته دیگری که وجود دارد این است که تداخلات بین سمبلی اکثرا موجب خرابی عملکرد می‌شوند، حتی در حالتی که در گیرنده از آشکارساز بهینه برای بازیابی سمبل‌های پیام استفاده شود.
یک راه دیگر برای طراحی یک سیستم مخابراتی با پهنای باند موثر در حضور اعوجاج کانال این است که پهنای باند کانال موجود را به تعدادی «زیرکانال» (Subchannels) با پهنای باندهای برابر تقسیم کنیم. این تقسیم باید به صورتی باشد که پهنای باند هر زیر کانال به اندازه کافی باریک باشد تا مشخصه پاسخ فرکانسی زیرکانال‌ها تقریبا ایده‌آل شود. این تقسیم پهنای باند کلی به زیرکانال‌های کوچک‌تر در تصویر زیر نشان داده شده است.
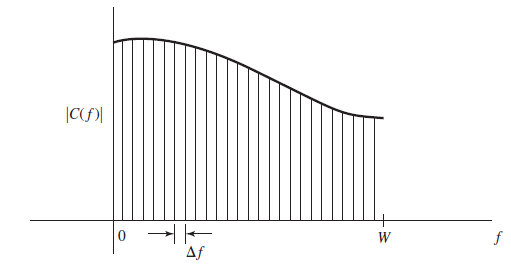
بنا بر آنچه تا کنون گفتیم، تعداد $$ K = W / \triangle f $$ زیرکانال می‌سازیم که سمبل‌های اطلاعات مختلف به صورت همزمان در این K زیرکانال منتقل شوند. در نتیجه این امر، اصطلاحا می‌گوییم که اطلاعات با روش تقسیم فرکانسی چندگانه یا FDM ارسال شده‌اند. در این روش هر زیر کانال متناظر با یک حامل است:
$$ x _ k ( t ) = \sin 2 \pi f _ k t \; \; \; \; \; k = 0 , 1 , ... , k - 1 $$
در این رابطه، $$ f _ k $$ برابر با فرکانس میانی در kاُمین زیرکانال است. با انتخاب نرخ داده برابر با $$ 1 / T $$ در هر کدام از زیرکانال‌ها که برابر با فاصله $$ \triangle f $$ از زیرکانال مجاور است، «زیرحامل‌ها» (Subcarriers) در بازه سمبل T متعامد می‌شوند و از رابطه فاز نسبی بین زیرحامل‌ها مستقل می‌شوند:
$$ \int _ { 0 } ^ { T } \sin ( 2 \pi f _ k t + \phi _ k ) \sin ( 2 \pi f _ i t + \phi _ j ) d t = 0 $$
در این رابطه، $$ f _ k − f _ j = n / T $$ و $$ n = 1 , 2 , . . . , $$ مستقل از مقادیر فازهای $$ \phi _ k $$ و $$ \phi _ j $$ است. به این حالت مدولاسیون تقسیم فرکانسی چندگانه متعامد یا OFDM می‌گویند. در یک سیستم OFDM که دارای k زیرکانال باشد، نرخ سمبل در هر زیرحامل با یک فاکتور N نسبت به نرخ سمبل در یک سیستم تک حاملی یا SC کاسته می‌شود. در یک سیستم تک حاملی از تمام پهنای باند W کانال استفاده می‌شود و نرخ انتقال داده آن برابر با روش OFDM است.
به همین دلیل بازه سمبل در مدولاسیون OFDM برابر با $$ T = K T _ S $$ است که $$ T _ S $$ بازه سمبل در سیستم تک حاملی است. با انتخاب k به اندازه کافی بزرگ، بازه سمبل T نیز به صورت قابل ملاحظه‌ای نسبت به طول زمان «پراکندگی زمانی کانال» (Channel Time Dispersion) بزرگ‌تر می‌شود. بنابراین می‌توان تداخلات بین سمبلی را از طریق انتخاب k کوچک‌تر کرد. به عبارت دیگر، هر زیر کانال پاسخ فرکانسی ثابت $$ C ( f _ k ) , k = 0, 1, . . . , K − 1 $$ خواهد داشت.
تا هنگامی که سنکرون زمانی را بین زیرحامل‌ها حفظ کنیم، مدولاسیون OFDM امکان انتقال سمبل یا بیت‌های متفاوت را روی هر زیر حامل فراهم می‌کند. به همین دلیل زیرحامل‌هایی که به دلیل تضعیف پایین‌تر، SNR بزرگ‌تری دارند، می‌توانند برای انتقال بیت‌های بیشتری (نسبت به زیرکانال‌های با SNR پایین‌تر) مدوله شوند. به عنوان مثال، ممکن است در یک سیستم OFDM از مدولاسیون QAM با اندازه خوشه‌های مختلف استفاده شود.
مدولاتور و دمدولاتور در یک سیستم مدولاسیون تقسیم فرکانسی چندگانه متعامد یا OFDM را می‌توان با استفاده از بانک‌های فیلتری موازی بر اساس تبدیل فوریه گسسته پیاده‌سازی کرد. زمانی که تعداد زیرکانال‌ها بزرگ باشد، مثلا $$ K > 25 $$، مدولاتور و دمدولاتور در یک سیستم OFDM به صورت موثری با کمک الگوریتم تبدیل فوریه سریع یا FFT برای محاسبه تبدیل فوریه گسسته پیاده‌سازی می‌شود. در قسمت‌های بعد، یک سیستم OFDM را بررسی خواهیم کرد که مدولاتور و دمدولاتور آن بر اساس تبدیل فوریه گسسته پیاده‌سازی شده‌اند.
یک مشکل عمده که در حالت کلی در مدولاسیون چند حاملی و در حالت خاص در مدولاسیون OFDM وجود دارد، مقادیر بزرگ نسبت توان پیک به میانگین یا PAR است که در سیگنال انتقالی به صورت ذاتی وجود دارد. در سیگنال ارسالی زمانی پیک‌های بزرگ اتفاق می‌افتد که سیگنال‌های زیرکانال k به صورت سازنده فاز اضافه می‌کنند. این چنین پیک‌های بزرگی در سیگنال ممکن است موجب اشباع تقویت کننده توان در فرستنده شوند و در نتیجه «اعوجاج مدولاسیون متقابل» (Intermodulation Distortion) در سیگنال ارسالی به وجود آید.
اعوجاج مدولاسیون متقابل را می‌توان کاهش داد و یا آن را به صورت کامل حذف کرد. برای این کار باید توان در سیگنال ارسالی کاهش داده شود که در نتیجه تقویت کننده توان در فرستنده در ناحیه خطی عمل می‌کند. البته این کاهش توان منجر به عملکرد غیرموثر سیستم OFDM می‌شود. روش‌های متنوعی برای کاهش PAR در سیستم‌های مدولاسیون چند حاملی به وجود آمده است. یکی از ساده‌ترین این روش‌ها، ایجاد شیفت فازهای مختلف در هر یک از زیرحامل‌ها است که شیفت فازها به صورت شبه‌تصادفی و یا به وسیله برخی الگوریتم‌ها انتخاب می‌شوند تا مقدار PAR کاهش داده شود.
پیاده‌سازی الگوریتم مدولاسیون OFDM به وسیله الگوریتم تبدیل فوریه سریع (FFT)
در این قسمت می‌خواهیم یک سیستم مدولاسیون OFDM را پیاده‌سازی کنیم که در آن از QAM برای انتقال داده روی هر یک از زیرحامل‌ها و از الگوریتم FFT برای پیاده‌سازی مدولاتور و دمدولاتور استفاده می‌شود.
بلوک دیاگرام پایه سیستم OFDM در تصویر زیر نشان داده شده است.
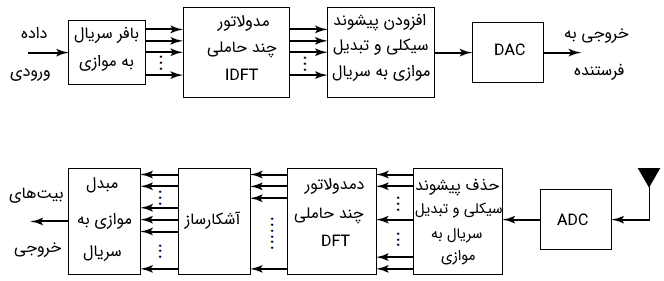
همان طور که در تصویر بالا نیز دیده می‌شود، یک بافر سریال به موازی رشته اطلاعات را به فریم‌های $$ B _ f $$ بیتی تقسیم می‌کند. $$ B _ f $$ بیت در هر فریم به k گروه تجزیه می‌شوند و به گروه iاُم $$ b _ i $$ بیت اختصاص داده می‌شود. در نتیجه می‌توان نوشت:
$$ \sum _ { i = 1 } ^ {k } b _ i = B _ f $$
مدولاتور چند حاملی را می‌توان به عنوان سیستمی برای تولید k زیرکانال QAM مستقل در نظر گرفت که نرخ سمبل در هر زیرکانال برابر با $$ 1 / T $$ و سیگنال‌ها در هر زیر کانال دارای خوشه مشخصی هستند. به همین دلیل تعداد نقاط سیگنال برای زیرکانال iاُم برابر با $$ \large M _ i = 2 ^ {b _ i } $$ است. حال فرض کنید نقاط سیگنال با مقادیر مختلط متناظر با سیگنال‌های اطلاعات در k زیرکانال را با $$ X _k , \; k = 0 , 1 , . . . , K − 1 $$ نشان دهیم.
سمبل‌های اطلاعات $$ \{ X _ k \} $$ نشان دهنده مقادیر تبدیل فوریه گسسته یا DFT مربوط به سیگنال مدولاسیون چند حاملی OFDM یعنی $$ x ( t ) $$ هستند که دمدولاسیون روی هر زیر حامل QAM است. به این دلیل که $$ x ( t ) $$ باید یک سیگنال با مقادیر حقیقی باشد، تبدیل فوریه گسسته N نقطه‌ای $$ \{ X _ k \} $$ آن در مشخصه تقارن صدق می‌کند. پس می‌توان نوشت:
$$ X _ { N − k } = X ^ * _ k $$
بنابراین با تعریف زیر از K سمبل اطلاعات، $$ N = 2 K $$ سمبل می‌سازیم:
$$ \begin {aligned}
X _ { N - k } &= X _ { k } ^ { * } , \quad k = 1 , 2 , \ldots, K - 1 \\
X _ { 0 } ^ { \prime } &= \operatorname { Re } \left ( X _ { 0 } \right) \\
X _ { N } &= \operatorname { Im } \left ( X _ { 0 } \right )
\end {aligned} $$
به این نکته توجه کنید که سمبل اطلاعات $$ X _ 0 $$ به دو بخش تقسیم می‌شود که هر دو آن‌ها حقیقی هستند. اگر رشته جدید سمبل‌ها را با $$ \left \{ X _ { k } ^ { \prime } , k = 0 , 1 , \ldots , N - 1 \right \} $$ نشان دهیم، تبدیل فوریه گسسته معکوس N نقطه‌ای به صورت نقاط حقیقی زیر خواهد بود:
$$ x _ { n } = \frac { 1 } { \sqrt { N } } \sum _ { k = 0 } ^ { N - 1 } X _ { k } ^ { \prime } e ^ { j 2 \pi n k / N} \quad \; \; \; n = 0 , 1 , \ldots , N - 1 $$
در این رابطه، $$ \frac { 1 } { \sqrt { N } } $$ یک فاکتور مقیاس‌دهی است. دنباله مقادیر $$ \{ x _ n , \; 0 \leq n \leq N - 1 \} $$ متناظر با نمونه‌های سیگنال تقسیم فرکانسی چندگانه متعامد $$ x ( t ) $$، از k زیرحامل تشکیل شده‌اند که می‌توان آن‌ها را به صورت زیر نشان داد:
$$ x _ { t } = \frac { 1 } { \sqrt { N } } \sum _ { k = 0 } ^ { N - 1 } X _ { k } ^ { \prime } e ^ { j 2 \pi k t / T } \quad \; \; \; 0 \leq t \leq T $$
در این رابطه T برابر با طول سیگنال و $$ x _ n = x ( n T / N ) , \; n = 0 , 1 , . . . , N − 1 $$ است. فرکانس‌های زیرحامل‌ها نیز به صورت زیر هستند:
$$ f _ k = k / T , \; \; \; k = 0 , 1, . . . , K − 1 $$
نمونه‌های سیگنال $$ \{ x _ n \} $$ که با محاسبه تبدیل فوریه گسسته معکوس تولید شده‌اند، از یک مبدل دیجیتال به آنالوگ یا DAC عبور داده می‌شوند که خروجی آن در حالت ایده‌آل برابر با شکل موج سیگنال OFDM یا تقسیم فرکانسی چندگانه متعامد $$ x ( t ) $$ است. $$ x ( t ) $$ برابر با ورودی کانال در نظر گرفته می‌شود. در این صورت سیگنال خروجی از کانال را می‌توان به صورت زیر نوشت:
$$ r ( t ) = x ( t ) * c ( t ) + n ( t ) $$
در این رابطه $$ c ( t ) $$ برابر با پاسخ ضربه کانال و * نماد عمل کانولوشن است. از آنجا که پهنای باند $$ \triangle f $$ هر زیرکانال به نحوی انتخاب شده است که نسبت به پهنای باند کلی کانال یعنی $$ W = K \triangle f $$ بسیار باریک باشد، در نتیجه طول سمبل $$ T = 1 / \triangle f $$ نسبت به طول پاسخ ضربه کانال بزرگ‌تر است. برای روشن‌تر شدن این مفهوم فرض کنید پاسخ ضربه کانال شامل m + 1 نمونه سیگنال باشد که $$ m \ll N $$ است.
یک روش بسیار ساده برای حذف کامل تداخلات بین سمبلی یا ISI، این است که یک «بازه زمانی محافظ» (Time Guard) یا باند محافظ با طول $$ m T / N $$ را در میان انتقال بلوکهای داده متوالی اعمال کنیم. اعمال یک فاصله زمانی، این امکان را به پاسخ کانال می‌دهد که قبل از ارسال بلوک بعدی متشکل از K سمبل، میرا شود. در تصویر زیر نمایی از مفهوم باند محافظ در مدولاسیون OFDM نشان داده شده است.
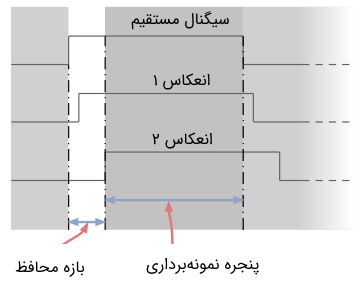
یک روش دیگر برای حذف تداخلات بین سمبلی این است که یک «پیشوند سیکلی» (Cyclic Prefix) به هر بلوک از N نمونه سیگنال $$ \{ x _ n, \; 0 ≤ n ≤ N − 1 \} $$ الحاق کنیم. پیشوند سیکلی برای بلوکهای نمونه‌های سیگنال از سمپل‌های $$ x _ { N - m }, x _ { N - m + 1 } , . . . , x _ { N - 1 } $$ تشکیل شده است. این نمونه‌ها به ابتدای بلوک الحاق می‌شوند و بنابراین رشته‌ای با طول N + m نمونه ایجاد می‌کنند که از n = - m تا n = N - 1 اندیس‌دهی می‌شوند و m نمونه نخست پیشوند سیکلی را تشکیل می‌دهند. در تصویر زیر مفهوم پیشوند سیکلی نشان داده شده است.
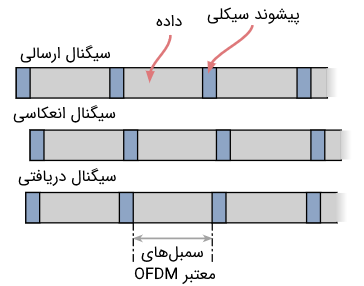
بنابراین اگر مقادیر نمونه‌های پاسخ کانال برابر با $$ \{ c _ n \;, \; 0 ≤ n ≤ m \} $$ باشند، آن گاه حاصل کانولوشن $$ \{ c _ n \} $$ با $$ \{ x _ n, \; - m ≤ n ≤ N − 1 \} $$ سیگنال دریافت شده $$ \{ r _ n \} $$ را ایجاد می‌کند. چون تداخلات بین سمبلی در هر جفت از بلوکهای انتقال سیگنال متوالی، روی m نمونه اول سیگنال تاثیر می‌گذارد، در نتیجه از m نمونه اول از $$ \{ r _ n \} $$ صرف نظر می‌کنیم و سیگنال را بر اساس نمونه‌های سیگنال دریافتی $$ \{ r _ n , \; 0 \leq n \leq N - 1 \} $$ دمدوله می‌کنیم.
اگر مشخصه‌های کانال را در حوزه فرکانس مشاهده کنیم، پاسخ فرکانسی کانال در فرکانس‌های زیرکانال $$ f _ k = k / T $$ به صورت زیر است:
$$ C _ { k } = C \left( \frac { 2 \pi k } { N } \right) = \sum _ { n = 0 } ^ { m } c _ { n } e ^ { - j 2 \pi n k / N }, \quad k = 0 , 1 , \ldots , N - 1 $$
چون اختلالات بین سمبلی با استفاده از پیشوند سیکلی و یا باند زمان محافظ از بین رفته است، در نتیجه رشته دمدوله شده از سمبل‌ها را می‌توان به صورت زیر نشان داد:
$$ \hat { X } _ { k } = C _ { k } X _ { k } ^ { \prime } + \eta _ { k } , \quad k = 0 , 1 , \ldots , N - 1 $$
که در این رابطه، $$ \{ \hat { X } _ { k } \} $$ برابر با خروجی تبدیل فوریه گسسته N نقطه‌ای است که توسط دمدولاتور محاسبه شده است و $$ \{ \eta _ { k } \} $$ برابر با نویز جمع شونده است که سیگنال را خراب می‌کند. همان طور که در تصویر قبل نشان داده شد، سیگنال دریافت شده با استفاده از محاسبه تبدیل فوریه گسسته آن سیگنال بعد از گذر از یک مبدل آنالوگ به دیجیتال یا ADC دمدولاسیون می‌شود. در مورد مدولاتور OFDM، محاسبه تبدیل فوریه گسسته در دمدولاتور به صورت موثر و با استفاده از الگوریتم تبدیل فوریه سریع یا FFT انجام می‌شود.
برای بازیابی سمبل‌های اطلاعات از روی مقادیر تبدیل فوریه گسسته به دست آمده، ضروری است که فاکتورهای کانال $$ \{ C _ { k } \} $$ را تخمین و جبران‌سازی کنیم. اندازه‌گیری کانال را می‌توان با استفاده از ارسال اولیه یک رشته مدوله شده معلوم روی هر یک از زیرحامل‌ها و یا به سادگی با استفاده از انتقال زیرحامل‌های مدوله نشده انجام داد. اگر مشخصه‌های کانال بسیار آهسته در زمان تغییر کنند، آن‌گاه می‌توان تغییرات زمانی را با استفاده از تصمیم‌گیری در خروجی آشکارساز تعقیب کرد. بنابراین سیستم چند حاملی مدولاسیون تقسیم فرکانسی چندگانه متعامد می‌تواند به صورتی ساخته شود که تطبیقی عمل کند.
نرخ انتقال داده روی هر یک از زیرحامل‌ها را می‌توان با انتخاب مناسب توان انتقالی متوسط و تعداد بیت‌هایی که توسط هر زیرحامل منتقل می‌شود، بهینه کرد. مقدار نسبت سیگنال به نویز یا SNR بر زیرکانال را می‌توان به صورت زیر تعریف کرد:
$$ \text { SNR } _ k = \frac { T P _ k { | C _ k |} ^ 2 } { \sigma ^ 2 _ { n k } } $$
در این رابطه $$ T $$ برابر با طول سمبل، $$ P _ k $$ توان انتقالی متوسط اختصاص داده شده به زیرکانال kاُم، $$ { | C _ k |} ^ 2 $$ مربع دامنه پاسخ فرکانسی kاُمین زیرکانال و $$ \sigma ^ 2 _ { n k } $$ واریانس نویز سیستم است. در زیرکانال‌های با نسبت سیگنال به نویز بزرگ نسبت به زیرکانال‌های با نسبت سیگنال به نویز کوچک، بیت یا سمبل‌های بیشتری را با استفاده از خوشه QAM بزرگ منتقل کرد. بنابراین نرخ بیت در هر زیرکانال را می‌توان به صورتی بهینه کرد که عملکرد نرخ خطا در بین زیرکانال‌ها برابر باشد و مشخصه‌های مطلوب را ارضا کند.
OFDM چند حاملی با استفاده از مدولاسیون QAM روی هر یک از زیرکانال‌ها که در بالا به توصیف آن پرداختیم، در کاربردهای بسیاری مورد استفاده قرار می‌گیرد که از آن جمله می‌توان به انتقال پرسرعت داده با استفاده از خطوط تلفن اشاره کرد.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزشهای مهندسی مخابرات
- آموزش مخابرات ۱
- مجموعه آموزشهای مهندسی الکترونیک
- آموزش مبانی الکترونیک – مفاهیم تئوریک به همراه شبیه سازی عملی و کاربردی
- مدولاسیون SSBSC چیست؟ — به زبان ساده
- گزینندگی کانال مجاور یا ACS در مخابرات چیست؟ — از صفر تا صد
- مدولاسیون کلیدزنی شیفت فاز یا PSK چیست؟ — از صفر تا صد
^^
سلام خيلي ممنون از مطالب مفيدتون.ميشه مقاله انگليسي درمورد ofdm به من معرفي كنيد
عالی هستین مثل همیشه.
مرسی که هستین