تقارن مرکزی چیست؟ — به زبان ساده + مثال

در آموزشهای پیشین مجله فرادرس، با تقارن محوری آشنا شدیم و ویژگیهای آن را بیان کردیم. در این آموزش، یکی دیگر از انواع تقارن، یعنی تقارن مرکزی را معرفی میکنیم و با ویژگیهای آن آشنا میشویم.
تقارن چیست؟
تقارن یکی از ویژگیهای اشکال هندسی است. اگر شکلی را جابهجا کنیم، بچرخانیم یا تحت بازتاب و تجانس قرار دهیم و تغییری در آن حاصل نشود، آنگاه میگوییم این شکل تقارن دارد.
آشنایی با انواع تقارن در هندسه
ابتدا انواع تقارن در هندسه را مرور میکنیم. تقارن را میتوان در هنگام چرخاندن، بازتاب یا لغزش یک شکل یا جسم مشاهده کرد. چهار نوع تقارن وجود دارد که در موارد مختلف قابل مشاهدهاند.
- تقارن انتقالی (Translational Symmetry)
- تقارن چرخشی (Rotational Symmetry)
- تقارن بازتابی (Reflexive Symmetry)
- تقارن لغزشی (Glide Symmetry)
تقارن انتقالی
اگر جسمی، با جهتگیری یکسان در حرکت رو به جلو و عقب، از موقعیتی به موقعیت دیگر منتقل شود، به آن «تقارن انتقالی» میگویند. به عبارت دیگر، تقارن انتقالی به عنوان لغزش یک جسم روی یک محور تعریف میشود. بهعنوان مثال، شکل زیر که در آن شکل با حفظ محور ثابت به جلو و عقب حرکت میکند، تقارن انتقالی را نشان میدهد.
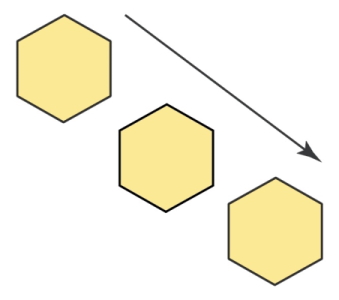
تقارن چرخشی
هنگامی که یک جسم در یک جهت خاص، حول یک نقطه میچرخد، به آن «تقارن چرخشی» میگویند که به «تقارن شعاعی» نیز معروف است. تقارن چرخشی زمانی وجود دارد که شکلی چرخانده شود و شکل با مبدأ یکسان باشد. زاویه تقارن دورانی کوچکترین زاویهای است که شکل میتواند در آن بچرخد تا با خودش منطبق شود و ترتیب تقارن نحوه انطباق جسم با خود در هنگام چرخش است.

در هندسه، اشکال زیادی وجود دارد که تقارن چرخشی دارند. به عنوان مثال، شکلهایی مانند دایره، مربع، مستطیل تقارن دورانی یا چرخشی دارند. تصویر بالا نشان میدهد که چگونه ساختار ستاره دریایی از تقارن چرخشی پیروی میکند. اگر ستاره دریایی را حول نقطه P بچرخانید، همچنان از همه جهات یکسان به نظر میرسد.

چرخ و فلک معروف، موسوم به «چشم لندن»، نمونهای از تقارن چرخشی است. ميتوانیم اشیاء زیادی را در زندگی واقعی پیدا کنید که دارای تقارن چرخشی هستند، مانند چرخها، آسیابهای بادی، تابلوهای جادهها، پنکههای سقفی و غیره.
تقارن بازتابی
تقارن بازتابی یا انعکاسی که تقارن آینهای نیز نامیده میشود، نوعی تقارن است که در آن نیمی از جسم، نیمه دیگر جسم را منعکس میکند. به عنوان مثال، به طور کلی، صورت انسان در سمت چپ و راست یکسان است و تقارن بازتابی دارد (البته بدون در نظر گرفتن چیزهایی مثل خال و مدل مو).

تقارن لغزشی
تقارن لغزشی ترکیبی از هر دو تبدیل انتقالی و بازتابی است. بازتاب لغزشی ماهیت جابهجایی دارد و تغییر در ترتیب (ابتدا انتقال رخ دهد یا ابتدا انتقال)، خروجی بازتاب لغزش را تغییر نمیدهد. تصویر متحرک زیر، تقارن لغزشی را بهخوبی نشان میدهد.

کاربردهای جالب تقارن
یک زیبابین (کالیدوسکوپ) آینههایی در داخل خود دارد که تصاویری را تولید میکند که دارای چندین خط تقارن هستند. زاویه بین آینهها تعداد خطوط تقارن را تعیین میکند.

پیش آمده است که چندین شیء متقارن را در زندگی روزمره خود مشاهده کرده باشیم، مانند رنگولی. جنبه قابل توجه تقارن را میتوان در طرحهای رنگولی مشاهده کرد. این طرحها در هند به دلیل نقوش منحصر به فرد و متقارن خود مشهور هستند. این شکلها علم رنگارنگ تقارن را به تصویر میکشند.
تقارن محوری چیست؟
تقارن محوری یکی از انواع تقارن است که نمونههای آن در اطرافمان بهوفور یافت میشود. وقتی شکلی نسبت به یک خط (یا محور) متقارن باشد، میگوییم تقارن نوع محوری دارد. شکل سمت چپ تصویر بخش قبل یک تقارن نوع محوری را نشان میدهد.
با یک مثال، تقارن محوری را بیشتر توضیح میدهیم. شکل زیر را در نظر بگیرید.
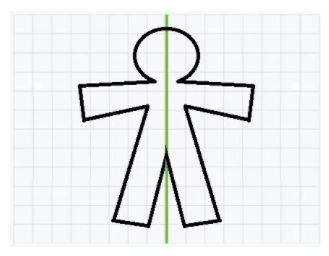
از میان سه عمل جابهجایی، چرخش و بازتاب، تقارن نوع محوری با عمل «بازتاب» تعریف میشود. برای وجود تقارن نوع محوری، باید خطی وجود داشته باشد بازتاب بخشی از شکل نسبت به آن، بخش دیگرش را بسازد. اما بازتاب چیست؟ عمل بازتاب را میتوان با یک تصور ساده درک کرد. برای مثال، آدمک شکل بالا را در نظر بگیرید. فرض کنید این آدمک را روی کاغذ رسم میکنیم. اگر کاغذ را دقیقاً روی خط سبز نشانداده شده در شکل تا کنیم، میبینیم که دو نیمه آن دقیقاً بر هم منطبق خواهند شد. این همان مفهموم بازتاب است.
تقارن مرکزی چیست؟
یکی از انواع مهم تقارن، تقارن مرکزی است. نام اصلی تقارن مرکزی، «تقارن نقطهای» (Point Symmetry) است که چون نقطه خاص مرکز یا همان مبدأ را در نظر میگیریم، به آن تقارن مرکزی میگوییم. یک جسم دارای تقارن مرکزی است اگر هر قسمت از جسم دارای در طرف دیگر نسبت به مرکز بازتاب داشته باشد. بدین صورت که اگر هر نقطه از شکل را در نظر بگیریم و از آن نقطه به مرکز یک خط رسم کنیم و خطا را در همان امتداد بهاندازه فاصله تا مبدأ ادامه دهیم، یک نقطه دیگر وجود داشته باشد.
شکل زیر تقارن مرکزی را بهخوبی نشان میدهد. به هریک از نقاط که بهدلخواه انتخاب شدهاند، دقت کنید. میبینیم که اگر دو نقطه مشابه (همرنگ) را به هم وصل کنیم، خط از مرکز میگذرد و فاصله هردو آن دو نقطه نسبت به مرکز با هم برابر است. در شکل زیر نقطه سبز مرکز است.
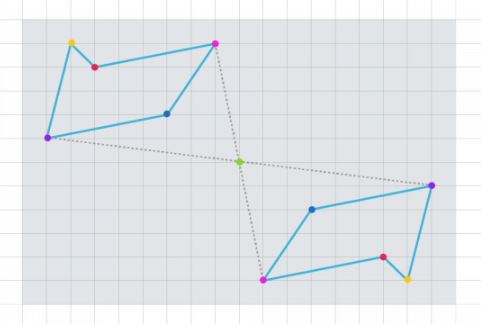
یک تعریف دیگر برای تقارن مرکزی این است: اگر شکلی دارای تقارن دورانی 180 درجه باشد، تقارن مرکزی دارد. بدین صورت که اگر کل یک شکل را بهاندازه ۱۸۰ درجه حول یک نقطه بچرخانیم، یک تقارن مرکزی ایجاد میشود.
ویدیوی کوتاه زیر تقارن مرکزی و چرخش ۱۸۰ درجهای حول نقطه مرکزی را بهخوبی نشان میدهد. میبینیم که اگر ۱۸۰ درجه یکی از شکلها را بچرخانیم، روی شکل دیگر منطبق میشود.
ویدیوی زیر نیز نشان میدهد که اگر شکل را ۱۸۰ درجه حول نقطه مرکز بچرخانیم، یک شکل با تقارن مرکزی خواهیم داشت.
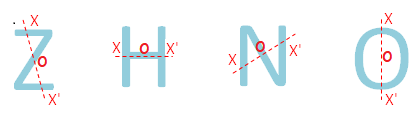
بسیاری از حروف الفبای انگلیسی تقارن مرکزی دارند. نقطه O نقطه مرکزی است و قسمتهای منطبق در جهت مخالف هستند.
دقت کنید، وقتی چیزی مثل یک پیکان تقارن مرکزی داشته باشد، باید جهت دو بخش آن مخالف هم باشند. شکل زیر این موضوع را بهخوبی نشان میدهد.
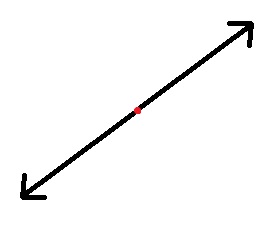
چگونه بفهمیم یک شکل تقارن مرکزی دارد؟
اما چگونه میتوان بررسی کرد که یک شکل نسبت به یک نقطه تقارن دارد یا خیر؟ یکی از راههای بررسی اینکه آیا یک شکل نسبت به یک نقطه (در اینجا مرکز) تقارن دارد، چرخاندن آن یک بخش آن بهاندازه ۱۸۰ درجه است. اگر شکل مشابه شکل اصلی باشد، نسبت به آن متقارن است. یک راه دیگر نیز این است که چمد نقطه دلخواه از شکل را انتخاب کنیم و خطی رسم کنیم که از مرکز بگذرد و آن خط را بهاندازه فاصله نقطه تا مرکز ادامه دهیم، اگر دو نقطه از دو بخش شکل روی یک خط باشند و فاصله آنها از مرکز برابر باشد و این شرط برای سایر نقاط دلخواه برابر باشد، شکل تقارن مرکزی خواهد داشت.
شکل زیر دو منحنی را نشان میدهد که نسبت به مبدأ تقارن دارند.
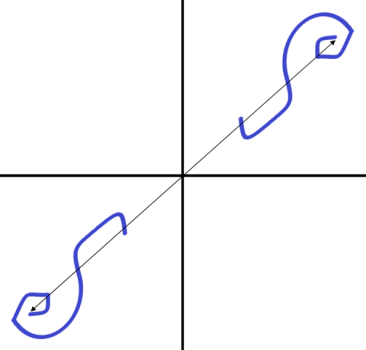
آیا دایره تقارن مرکزی دارد؟
جواب به این سؤال مثبت است. مرکز دایره مرکز تقارن آن است.
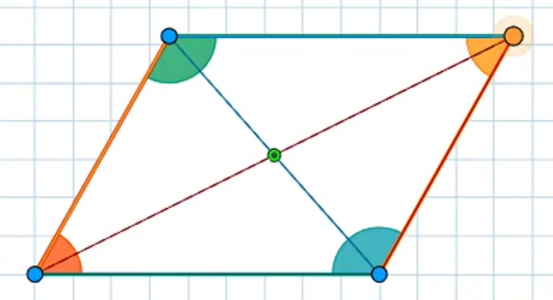
آیا متوازیالاضلاع مرکز تقارن دارد؟
محل تقاطع دو قطر متوازیالاضلاع مرکز تقارن آن است. اگر این شکل را روی کاغذ رسم کنیم و حول مرکز بهاندازه ۱۸۰ درجه بچرخانیم، میبینیم که روی خودش منطبق میشود.
آیا مستطیل تقارن مرکزی دارد؟
مستطیل و مربع شکلهایی هستند که تقارن مرکزی دارند.
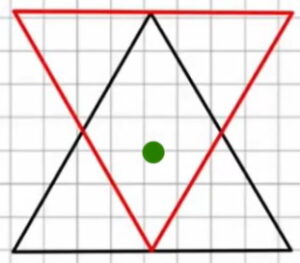
آیا مثلث تقارن مرکزی دارد؟
اگر مثلث سیاه را ۱۸۰ درجه نسبت به نقطه سبز دوران دهیم، میبینیم که مثلث قرمز حاصل میشود. به دلیل اینکه با ۱۸۰ درجه چرخش، مثلث قرمز روی مثلث سیاه منطبق نمیشود، نتیجه میگیریم کخ مثلث تقارن مرکزی ندارد.
مثالهای تقارن مرکزی
در این بخش، مثالهایی را از تقارن مرکزی بررسی میکنیم.
مثال اول
تعیین کنید که آیا شکل زیر تقارن مرکزی دارد یا خیر.
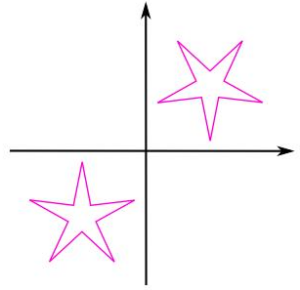
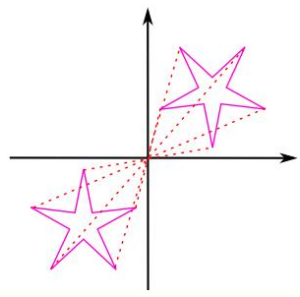
جواب: بله. در شکل داده شده بالا، هر قسمت از شکل دارای یک قسمت منطبق با نقطه مرکز است. همچنین، اگر دو شکل را نسبت به مبدأ بسنجیم، میبینیم که تقارن دارند. شکل زیر بهخوبی این تقارن را نشان میدهد.
مثال دوم
آیا شکل زیر تقارن مرکزی دارد؟
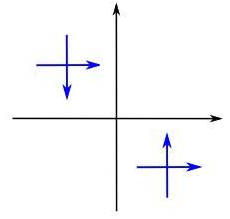
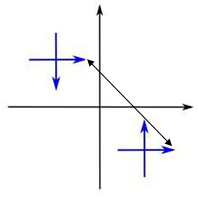
جواب: خیر، شکل داده شده در بالا یکی از شروط تقارن مرکزی را برآورده نمیکند. به این معنا که، جهت پیکانها در دو شکل باید مخالف باشد و نیست. شکل زیر این موضوع را بهخوبی نشان میدهد. به دو فلش سمت راست دقت کنید که نسبت به مبدأ تقارن ندارند.
مثال سوم
بیان کنید که آیا شکل زیر در مورد یک نقطه تقارن دارد یا خیر.
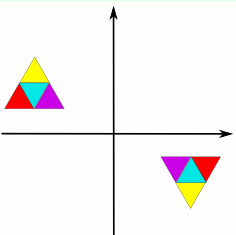
جواب: بله. در شکل داده شده در بالا، اگر هریک از دو مثلث را حول مبدأ بهاندازه ۱۸۰ درجه بچرخانیم، بر مثلث دیگر منطبق میشود. از طرفی، شکل زیر بهخوبی تقارن مرکزی را نمایش میدهد.
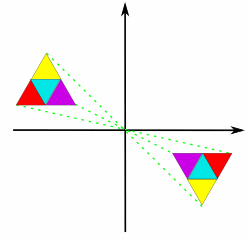
مثال چهارم
آیا شکل زیر نسبت به نقطه مبدأ متقارن است؟
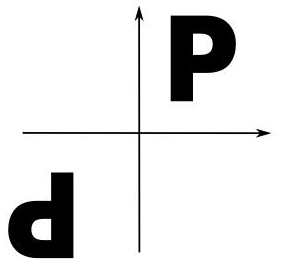
جواب: خیر. شکل زیر بهخوبی نشان میدهد که اگر نقطه مشابهی از دو شکل را در نظر بگیریم، فاصله یکسانی از نقطه مبدأ ندارند.
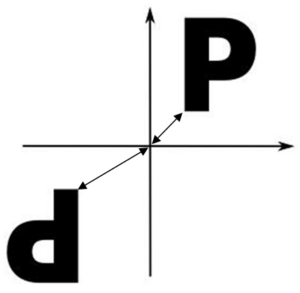
مثال پنجم
آیا شکل زیر نسبت به مبدأ متقارن است؟

جواب: بله. برای شکل بالا میتوان گفت هر نقطه از شکل یک نقطه متقارن نسبت به نقطه مرکزی دارد که در جهت مخالف آن است. شکل زیر تقارن مرکزی را بهخوبی نشان میدهد.
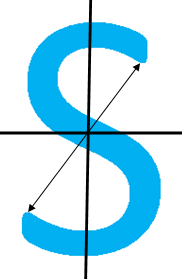
مثال ششم
شکل زیر را در نظر بگیرید. آیا این شکل متقارن است؟ اگر پاسخ مثبت است، نوع تقارن را بیان کنید.
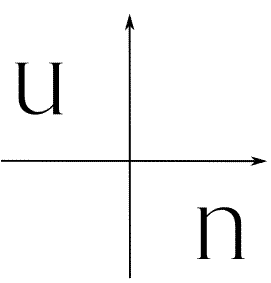
جواب: میبینیم که هر نقطه از یکی از دو شکل را انتخاب کنیم، متقارن آن نسبت به مبدأ روی شکل دیگر وجود دارد. شکل زیر تقارن مرکزی را بهخوبی نشان میدهد.
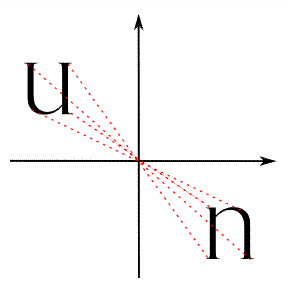
مثال هفتم
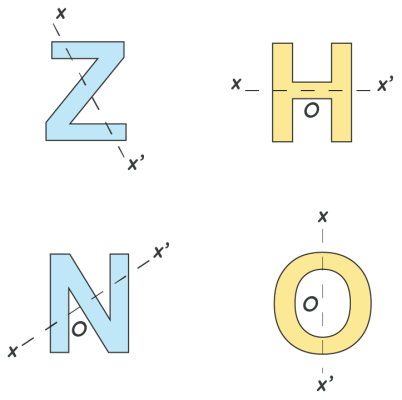
از بین حروف الفبای انگلیسی Z و H و N و O، کدامیک تقارن مرکزی دارند؟
جواب: شکل زیر بهخوبی نشان میدهد که همه این حروف تقارن مرکزی دارند.
جمعبندی
در این آموزش، ابتدا به معرفی تقارن و انواع آن پرداختیم. سپس، مطالبی را درباره تقارن مرکزی و ویژگیهای آن بیان کردیم. در نهایت، مثالهایی متنوعی از تقارن مرکزی را مورد بررسی قرار دادیم.












درود. سپاس از زحمتی که می کشید. اما کاش فایل پی دی اف یا ورد مطالب را هم به اشتراک می گذاشتید.