فرادرستبدیل منبع در مدار — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
در آموزش‌های قبلی مجله فرادرس با مقاومت‌های سری و موازی و تبدیل ستاره-مثلث برای ساده‌سازی مدارهای الکتریکی آشنا شدیم. در این آموزش، با ابزار دیگری به نام تبدیل منبع آشنا می‌شویم که با کمک آن می‌توان مدارها را ساده‌سازی کرد. اساس این ابزار، مفهوم معادل بودن است. مشخصه جریان-ولتاژ مدار معادل، مشابه با مدار اصلی است.
روش تبدیل منبع در مدار
همان‌طور که می‌دانیم، معادلات ولتاژ گره (یا جریان مش) را می‌توان با تحلیل یک مدار، وقتی که منابع همه منبع جریان مستقل (یا ولتاژ مستقل) باشند، به دست آورد.
بنابراین، گاهی لازم است در تحلیل مدار، منبع ولتاژ سری با مقاومت را با منبع جریان موازی با مقاومت یا بالعکس جایگزین کنیم. هر کدام از این جایگزینی‌ها یک «تبدیل منبع» (Source Transformation) نامیده می‌شود.
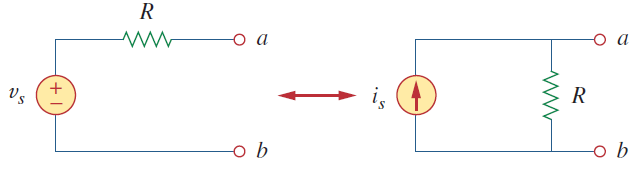
در واقع می‌توان گفت که تبدیل منبع فرایند جایگزینی منبع ولتاژ $$V _ S$$ سری با مقاومت $$R$$ با منبع جریان $$i _ S $$ موازی با مقاومت $$R$$ و بالعکس است.
دو مدار شکل بالا، معادل هستند و رابطه ولتاژ-جریان در ترمینال‌های $$a-b $$ آن‌ها با هم مشابه است. معادل بودن این دو مدار را به سادگی می‌توان نشان داد. اگر منابع خاموش باشند، مقاومت معادل در ترمینال‌های $$a-b$$ هر دو مدار برابر با $$R$$ است. همچنین، وقتی ترمینال‌های $$a-b$$ اتصال کوتاه شوند، جریان اتصال کوتاهی که از $$a$$ به $$b$$ می‌گذرد، در مدار سمت چپ برابر با $$ i _ { s c } = v _ s / R $$ و در مدار سمت راست برابر با $$ i _ { s c } = i _ s $$ است. بنابراین، از آنجایی که دو مدار معادل هستند، رابطه $$ v _ s / R = i _ s $$ برقرار است. در نتیجه، شرط تبدیل منابع، برقراری رابطه زیر است:
$$ \large v _ s = i _ s R $$ یا $$ \large i _ s = \frac { v _ s } { R } $$
تبدیل منابع را می‌توان به منابع وابسته نیز اعمال کرد. در این مورد باید به متغیرهای وابسته دقت کنیم. همان‌گونه که در شکل ۲ نشان داده شده است، یک منبع ولتاژ وابسته سری با مقاومت را می‌توان به منبع جریان موازی با مقاومت و بالعکس تبدیل کرد. البته باید شرایط معادله‌ای که در بالا ذکر شد برقرار باشد.
مشابه تبدیل ستاره-مثلث که قبلاً با آن آشنا شدیم، تبدیل منبع اثری بر سایر بخش‌های مدار ندارد. تبدیل منبع، در صورتی که بتوان از آن استفاده کرد، ابزار قدرتمندی است که با استفاده از آن می‌توان تحلیل مدار را تسهیل کرد. البته، هنگام استفاده از روش تبدیل منابع باید موارد زیر را در نظر بگیریم:
- در شکل‌های ۱ و ۲، جهت منبع جریان به سمت پلاریته مثبت منبع ولتاژ است.
- طبق معادله‌ای که در بالا بیان شد، وقتی $$R = 0 $$ باشد، تبدیل منبع ولتاژ امکان پذیر نیست. همچنین، عملاً نمی‌توانیم یک منبع جریان ایده‌آل (با $$ R = \infty$$) را با یک منبع ولتاژ محدود جایگزین کنیم.
مثال‌ها
در این بخش دو مثال را از کاربرد تبدیل منابع در تحلیل مدار بیان می‌کنیم.
مثال ۱
با استفاده از تبدیل منبع، مقدار $$ v _ o $$ را در مدار زیر محاسبه کنید.
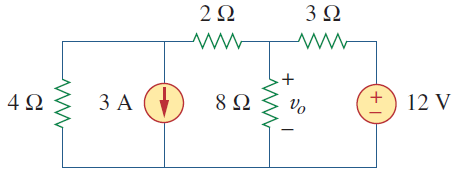
حل: ابتدا منابع ولتاژ و جریان را تبدیل می‌کنیم و به مدار شکل ۴ (الف) می‌رسیم.
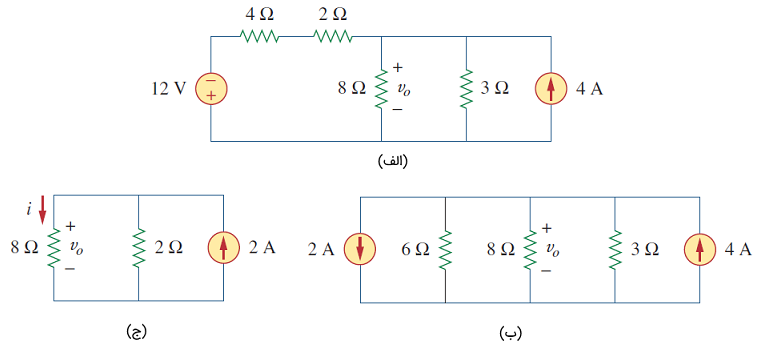
ترکیب سری دو مقاومت ۴ و ۲ اهمی و تبدیل منبع ولتاژ ۱۲ ولتی منجر به شکل ۴ (ب) خواهد شد. اکنون دو مقاومت موازی ۳ و ۶ اهمی را ترکیب می‌کنیم که حاصل آن ۲ اهم است. در ادامه، دو منبع جریان موازی را با هم ساده کرده و به یک منبع جریان ۲ آمپری می‌رسیم که جهت آن به بالا است.
در نهایت، با انجام مراحل فوق و استفاده از تبدیل منابع، به مدار شکل ۴ (ج) می‌رسیم.
اکنون از رابطه تقسیم جریان استفاده می‌کنیم و داریم:
$$ \large i = \frac {2 } { 2 + 8 } (2) = 0.4 \, \text{A}$$
و
$$ \large v _ o = 8 i = 8 ( 0.4) = 3.2 \, \text{V}$$
از آنجایی که دو مقاومت ۸ و ۲ اهمی در شکل ۴ (ج) موازی هستند، ولتاژ آن‌ها برابر با $$ v _ o $$ است. در نتیجه، می‌توان نوشت:
$$ \large v _ o = ( 8 || 2 ) ( 2 \, \text{A}) = \frac { 8 \times 2 } { 10 } ( 2 ) = 3.2 \, \text{V} $$
مثال ۲
جریان $$v _ x $$ مدار شکل ۵ را محاسبه کنید.
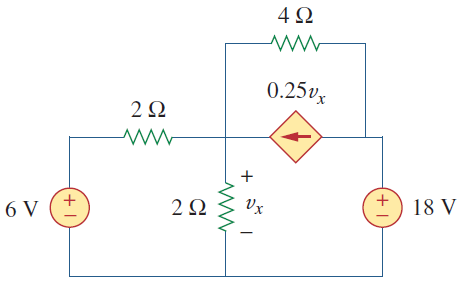
حل: مدار شکل ۵، شامل یک منبع جریان کنترل شده با ولتاژ است. این منبع وابسته را مطابق شکل ۶ (الف) به یک منبع ولتاژ وابسته تبدیل می‌کنیم. نیازی به تبدیل منبع ولتاژ ۱۸ ولتی نیست، زیرا مقاومت سری با آن وجود ندارد. دو مقاومت ۲ اهمی موازی را ساده می‌کنیم که به یک مقاومت ۱ اهمی می‌انجامد. خود مقاومت ۱ اهمی با منبع جریان ۳ آمپری موازی است.
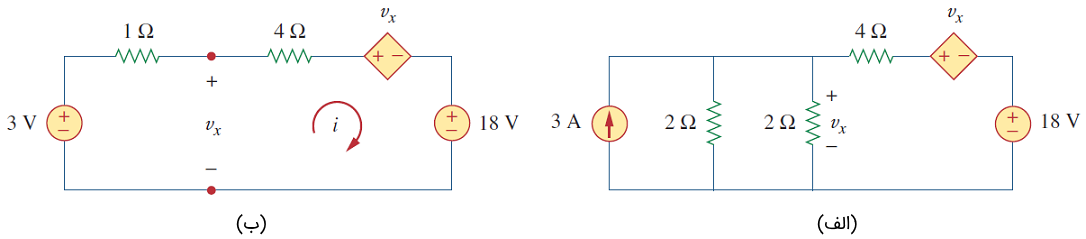
طبق شکل ۶ (ب)، منبع جریان را به یک منبع ولتاژ تبدیل می‌کنیم. توجه کنید که ولتاژ $$ v _ x $$ بدون تغییر باقی می‌ماند.
با اعمال قانون ولتاژ کیرشهف (KVL) در حلقه مدار شکل ۶ (ب)، داریم:
$$ \large - 3 + 5 i + v _ x + 18 = 0 $$
مجدداً اگر قانون ولتاژ کیرشهف را در حلقه‌ای که تنها شامل منبع ولتاژ ۳ ولتی و مقاومت ۱ اهمی است اعمال کنیم، ولتاژ $$v _ x $$ به صورت زیر به دست می‌آید:
$$ \large - 3 + 1 i + v _ x = 0 \; \; \; \; \Rightarrow \; \; \; \; v _ x = 3 -i $$
با ترکیب دو معادله اخیر، داریم:
$$ \large 15 + 5 i + 3 - i = 0 \; \; \; \; \Rightarrow \; \; \; \; i = - 4.5 \, \text {A} $$
همچنین، می‌توانیم KVL را بر حلقه شامل $$ v _ x $$، مقاومت ۴ اهمی، منبع ولتاژ کنترل شده با جریان و منبع ولتاژ ۱۸ ولتی در شکل ۶ (ب) اعمال کنیم:
$$ \large - v _ x + 4 i + v _ x +18 = 0 \; \; \; \; \Rightarrow \; \; \; \; i = - 4.5 \, \text {A} $$
در نتیجه، خواهیم داشت:
$$ \large v _ x = 3 - i = 7 . 5 \, \text{V}$$
اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
^^
فیلم های آموزش تبدیل منبع در مدار — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
فیلم آموزشی تبدیل منابع در مدار
فیلم آموزشی حل چند مثال از تبدیل منابع در مدار
بسیار ممنونم از اموزش زیبا و روانتون
موفق و سربلند باشید
سلام
استفاده کردم خدا خیرتون بده انشاالله طاعات وعباداتتان قبول حق .
سلام احمد عزیز.
از اینکه این آموزش بریتان مفید بوده است، بسیار خوشحالیم.
شاد و پیروز باشید.
سلام؛ خیلی ممنون از مطالب مفیدتون.
سلام دستت درد نکنه ، استفاده کردم و یاد گرفتم.