ادمیتانس — به زبان ساده

در راستای تکمیل مجموعه مقالات مجله فرادرس در حوزه فیزیک الکتریسیته و مهندسی برق، در این مقاله قصد داریم تا با زبانی ساده به مقوله ادمیتانس در مدارهای الکتریکی بپردازیم. با ما در ادامه مطلب همراه باشید.
امپدانس
در دو مقاله «برخی پارامترهای رایج در مهندسی برق — به زبان ساده» و «امپدانس و محاسبه آن -- به زبان ساده»، با پارامتر «امپدانس» (Impedance) یک مدار آشنا شدید. به طور کلی امپدانس یک عدد مختلط، یعنی از دو بخش حقیقی مقاومتی و بخش موهومی واکنشی (از جنس مقاومت) تشکیل شده و به صورت زیر نشان داده میشود:
(1)
مطابق با رابطه فوق، قسمت حقیقی امپدانس همان مقاوت و قسمت موهومی آن راکتانس است. میدانیم که مطابق با قانون اهم، رابطه میان ولتاژ و جریان به صورت است. اگر مدار فقط متشکل از مقاومت باشد، ولتاژ و جریان اختلاف فاز صفر درجه داشته و به اصطلاح همفاز هستند. در مقالات «خازن در جریان متناوب -- به زبان ساده» و «عناصر پسیو (Passive) در مدارهای AC — به زبان ساده» دیدیم که اگر عناصری نظیر خازن یا سلف که نسبت به عبور جریان متناوب از خود مقاومتی موسوم به «راکتانس» (Reactance) نشان میدهند، وجود داشته باشد، اختلاف فاز بین ولتاژ و جریان به اندازه 90 درجه میشود. پس رابطه امپدانس به طور کاملتر به فرم زیر در میآید:
(2)
توجه داشته باشید که راکتانس خازنی به صورت علامت منفی در محاسبات ظاهر میشود. یادآور میشویم که در مداری با منبع تغذیه متناوب و یک خازن، جریان به اندازه 90 درجه جلوتر و در سلف، به اندازه 90 درجه عقبتر از ولتاژ است. جهت یادآوری به نمایش فازوری شکل (1) دقت کنید.
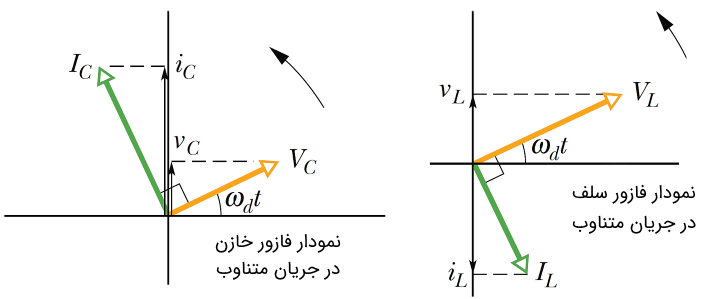
ادمیتانس
معکوس امپدانس را «ادمیتانس» (Admittance) نامیده که آن را با نماد نشان میدهند. پس داریم:
(3)
در نتیجه از قانون اهم، رابطه بین ولتاژ و جریان به صورت زیر در میآيد:
(4)
از آنجا که در مخرج رابطه ادمیتانس عددی مختلط وجود دارد، میتوانیم با ضرب مزدوج مختلط امپدانس در صورت و مخرج رابطه (۲)، ادمیتانس را به صورت زیر بنویسیم:
(5)
رابطه فوق را میتوان به صورت زیر نوشت که در آن «کنداکتانس» (Conductance) و سوسپتانس (Susceptance) است.
(6)
دو پارامتر کنداکتانس و سوسپتانس نیز به صورت زیر تعریف میشوند:
(7)
(8)
در سیستم بینالمللی واحد کمیتهای ادمیتانس ، کنداکتانس و سوسپتانس «زیمنس» (Siemens) است که با نماد یا نمایش داده میشود. همچنین واحد نیز به طور غیر رسمی برای آنها به کار میرود. در واقع طبق رابطه و از آنجا که واحد امپدانس اهم (Ω) است، واحد را که عکس واژه است، به کار میبرند.
از دو رابطه (۷) و (۸) میتوان بخش مقاومتی و واکنشیِ (راکتانس) رابطه امپدانس را به صورت زیر بر حسب دو پارامتر و نوشت:
(9)
(10)
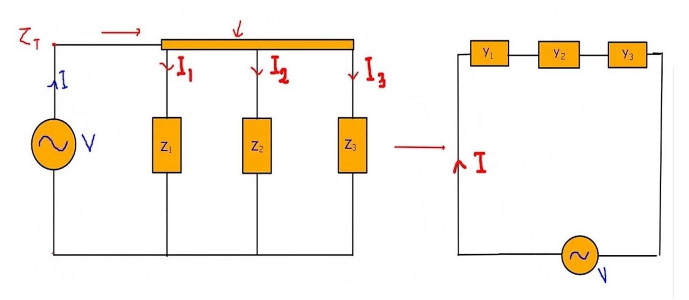
دیدیم که ادیمتانس چیزی جز معکوس امپدانس نیست. از آنجا که ماهیت ادمیتانس و امپدانس هر دو مقاومتی است، جهت راحتی کار در تحلیل مدار داریم:
امپدانس معادل مدار سری:
(11)
و ادمیتانس معادل مدار موازی:
(12)
رابطه فوق در واقع از روی فرمول مقاوت معادل موازی به دست میآید.
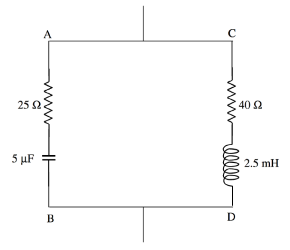
مثال
امپدانس مدار شکل (2) که متصل به منبع تغذیه جریان متناوبی به فرکانس را به دست آورید:
برای راکتانس خازنی و سلفی دو رابطه زیر را داشتیم:
طبق رابطه (۱) و محاسبه راکتانس خازن و راکتانس سلف از دو رابطه فوق، امپدانس را در دو شاخه و محاسبه میکنیم.
حال طبق رابطه (5) و سادهسازی ریاضی، ادمیتانس دو شاخه و را مینویسیم. همچنین برای راحتی استفاده از رابطه (12)، مخرج دو رابطه را یکسان کردیم.
پس ادمیتانس معادل (کل) مدار شکل (2) به صورت زیر در میآید:
با معکوس کردن ، امپدانس معادل مدار به دست میآید.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مدار الکتریکی — مفاهیم و کاربردها
- امپدانس ورودی (Input Impedance) تقویت کننده — مفاهیم کلیدی
- خازن در جریان متناوب -- به زبان ساده
- خازن موازی — به زبان ساده
^^













تو مثال که ادمیتانس cd رو حساب میکردید مخرج میشه ۱۷۰۰ بعد با صورت ساده میشه و میشه ۱۷۰ ولی اشتباهی مقدارمجذور Rو X رو از هم کم کردید و شده ۱۵۰۰ که بعد ساده کردید شد ۱۵۰
که غلطه
سلام.
متن اصلاح شد.
سپاس از همراهی و بازخوردتان.
خیلی عالی و قابل درک. دمتون گرم.