اتصال موازی سلف ها — به زبان ساده

در آموزشهای قبلی مجله فرادرس، با اتصال سری سلفها آشنا شدیم. در این آموزش، در مورد اتصال موازی سلف ها بحث خواهیم کرد. به طور خلاصه میتوان گفت ولتاژی که روی تک تک سلفهای موازی میافتد، با هم برابر است. به عبارت دیگر، سلفهای موازی ولتاژ مشترک و یکسانی دارند.
$$\large V_{L1}=V_{L2}=V_{L3}=V_{AB}...\,etc$$
در شکل زیر، سلفهای $$L_1$$، $$L_2$$ و $$L_3$$ بین دو نقطه $$A$$ و $$B$$ با یکدیگر موازی هستند.
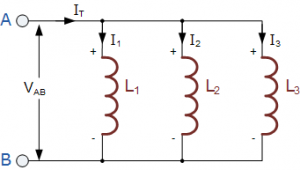
از آموزش قبلی در مورد اتصال سری سلفها میدانیم که اندوکتانس معادل چند سلف سری شده ($$L_T$$) برابر با مجموع اندوکتانس تک تک سلفها است. اما اندوکتانس معادل چند سلف موازی شده به شکل متفاوتی محاسبه میشود که در ادامه توضیح خواهیم داد.
با توجه به «قانون جریان کیرشهف» (Kirchoff’s Current Law) یا $$KCL$$، مجموع جریانهای گذرنده از سلفهای شکل بالا برابر است با:
$$\large I_{T}=I_{1}+I_{2}+I_{3}$$
همچنین، از آموزشهای قبلی در مورد سلف میدانیم که ولتاژ (نیرو محرکه الکتریکی) دو سر سلف برابر است با:
$$\large V=L\frac{di}{dt}$$
بنابراین با جایگذاری جریان سلفها ($$I_1+I_2+I_3$$) در معادله ولتاژ دور سر سلف داریم:
$$\large V_{AB}=L_T\frac{d}{dt}\left(i_1+i_2+i_3\right)=L_T\left(\frac{di_1}{dt}+\frac{di_2}{dt}+\frac{di_3}{dt}\right)$$
با جایگزینی $$\frac{di}{dt}$$ با $$\frac{v}{L}$$ معادله زیر به دست میآید:
$$\large V_{AB}=L_T\left(\frac{v}{L_1}+\frac{v}{L_2}+\frac{v}{L_3}\right)$$
با حذف مقدار ولتاژ از دو طرف معادله، فرمول نهایی برای محاسبه اندوکتانس سلفهای موازی به صورت زیر به دست میآید:
$$\large \frac{1}{L_T}= \frac{1}{L_1}+ \frac{1}{L_2}+ \frac{1}{L_3}\,...\,+ \frac{1}{L_N}$$
در اینجا، مشابه محاسبه مقاومت موازی معادل، به جای جمع تک تک اندوکتانسها، مقدار معکوس همهی اندوکتانسها ($$ \frac{1}{L_n}$$) با هم جمع میشود. البته مشابه اتصال سری سلفها، معادله بالا تنها در حالتی درست است که هیچگونه اندوکتانس متقابل یا تزویج مغناطیسی بین سلفها وجود نداشته باشد (از نظر مغناطیسی، همه سلفها نسبت به یکدیگر ایزوله باشند). اگر تزویجی بین سلفها وجود داشته باشد، بر مقدار اندوکتانس معادل سلفهای موازی تاثیر میگذارد.
فرمول بالا برای هر تعداد سلف موازی شده با یکدیگر به کار میرود. با این وجود، زمانی که تنها دو سلف با یکدیگر موازی باشد، میتوان فرمول ساده زیر را به کار برد:
$$\large L_{T}=\frac{L_1\times L_2}{L_1+L_2}$$
یک موضوع خیلی مهم در موازی کردن سلفها، این است که همواره اندوکتانس معادل چند سلف موازی، از اندوکتانس کوچکترین سلف مجموعه که با هم موازی شدهاند، کمتر خواهد بود.
مثال ۱
سه سلف با اندازههای $$60\,mH$$، $$120\,mH$$ و $$75\,mH$$ به صورت موازی به یکدیگر متصل شدهاند و هیچگونه اندوکتانس متقابلی بین آنها وجود ندارد. اندوکتانس معادل سلفهای موازی را محاسبه کنید.
حل:
$$\large \frac{1}{L_T}=\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3}$$
$$\large \, \therefore\,L_T=\frac{1}{\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_2}}=\frac{1}{\frac{1}{60\,mH}+\frac{1}{120\,mH}+\frac{1}{75\,mH}}$$
$$\large L_T=\frac{1}{38.333}=26\,mH$$
سلفهای موازی شده با القای متقابل
سلفهایی را در نظر بگیرید که به صورت موازی به یکدیگر متصل هستند و توسط شار مغناطیسی با هم پیوند دارند. در این حالت، با توجه به مقدار تزویج مغناطیسی بین سیمپیچها، اندوکتانس متقابل تغییر خواهد کرد و در نتیجه اندوکتانس معادل سلفهای موازی، نسبت به حالت بدون شار مغناطیسی، افزایش یا کاهش مییابد. تاثیر این اندوکتانس متقابل، بر اساس فاصله سیمپیچها و موقعیت آنها نسبت به یکدیگر تعیین میشود.
جمع یا تفریق شدن اندوکتانس معادل سلفهای موازی با القای متقابل را با یک نقطه که نشانگر پلاریته سلف است نشان میدهند. این موضوع را در شکل زیر مشاهده میکنید.
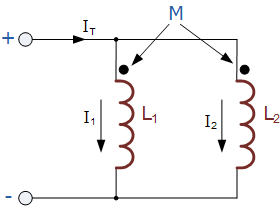
با توجه به شکل بالا، جریان گذرنده از سلف اول ($$L_1$$) برابر با $$I_1$$ و جریان گذرنده از سلف دوم ($$L_2$$) برابر با $$I_2$$ است. با توجه به موازی بودن دو سلف، ولتاژ دو سر آنها با یکدیگر برابر است. بنابراین، در حالت بالا که دو سلف موازی دارای پلاریته موافق هستند، اندوکتانس معادل برابر است با:
$$\large L_T=\frac{L_1L_2\,-M^2}{L_1+L_2-2\,M}$$
که در آن، $$2\,M$$ نشاندهنده تاثیر سیمپیچ $$L_1$$ بر سیمپیچ $$L_2$$ یا بالعکس است.
اگر اندوکتانس دو سلف با یکدیگر برابر و همچنین تزویج مغناطیسی بین آنها کامل باشد، اندوکتانس معادل حالت موازی شده، با اندوکتانس هر یک از آنها برابر است ($$L_T=L_1=L_2=M$$). همچنین، مشابه دو سلف با اندوکتانس خودی که با هم موازی هستند، اگر اندوکتانس متقابل صفر باشد، اندوکتانس معادل برابر با $$L\div2$$ است.
اگر یکی از دو سلف نسبت به دیگری معکوس باشد، در این صورت اندوکتانس متقابل بین دو سلف، تاثیر خنثی کنندگی بر سیمپیچها دارد. این حالت در شکل زیر نشان داده شده است.
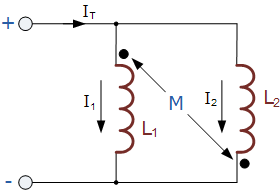
اندوکتانس معادل سلفها در این حالت برابر است با:
$$\large L_T=\frac{L_1L_2\,-M^2}{L_1+L_2+2\,M}$$
در این حالت، اگر اندوکتانس دو سلف باهم برابر و تزویج مغناطیسی بین آنها کامل باشد، به دلیل اینکه دو سلف اثر هم را خنثی میکنند، اندوکتانس معادل آنها برابر با صفر است. این حالت مشابه شرایطی است که دو سلف با اندوکتانس خودی و با پلاریته معکوس، با هم موازی هستند.
به عبارت دیگر، میتوان گفت که سلفها در زمان عبور جریان، «اتصال کوتاه» (Short Circuit) میشوند و اندوکتانس معادل آنها برابر با $$\left(L\pm M\right)\div2$$ است.
مثال ۲
دو سلف با اندازههای $$75\,mH$$ و $$55\,mH$$ به صورت موازی به یکدیگر متصل شدهاند. همچنین، تزویج مغناطیسی بین دو سلف به صورت موافق است (دو سلف دارای پلاریته هم جهت هستند). اندوکتانس متقابل برابر با $$22.5\,mH$$ است. اندوکتانس معادل این دو سلف موازی را محاسبه کنید.
حل:
$$\large L_T=\frac{L_1\times L_2\,-M^2}{L_1+L_2-2\,M}$$
$$\large L_T=\frac{75\,mH\times 55\,mH\,-22.5\,mH^2}{75\,mH+55\,mH-2\times22.5\,mH}$$
$$\large L_T=42.6\,mH$$
مثال ۳
اندوکتانس معادل مدار سلفی زیر را محاسبه کنید.
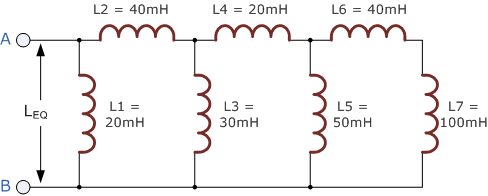
حل:
در ابتدا، اندوکتانس معادل شاخه $$L_A$$ (سلف $$L_5$$ موازی شده با دو سلف $$L_6$$ و $$L_7$$) را محاسبه میکنیم:
$$\large L_A=\frac{L_5\times\left(L_6+L_7\right)}{L_5+L_6+L_7}=\frac{50\,mH\times\left(40\,mH+100\,mH\right)}{50\,mH+40\,mH+100\,mH}=36.8\,mH$$
سپس، اندوکتانس معادل شاخه $$L_B$$ (سلف $$L_۳$$ موازی شده با دو سلف $$L_۴$$ و $$L_A$$) را به دست میآوریم:
$$\large L_B=\frac{L_3\times\left(L_4+L_A\right)}{L_3+L_4+L_A}=\frac{30\,mH\times\left(20\,mH+36.8\,mH\right)}{30\,mH+20\,mH+36.8\,mH}=19.6\,mH$$
در انتها، محاسبات اندوکتانس معادل مدار $$L_{EQ}$$ (سلف $$L_۱$$ موازی شده با دو سلف $$L_۲$$ و $$L_B$$) را انجام میدهیم:
$$\large L_{EQ}=\frac{L_1\times\left(L_2+L_B\right)}{L_1+L_2+L_B}=\frac{20\,mH\times\left(40\,mH+19.6\,mH\right)}{20\,mH+30\,mH+19.6\,mH}=15\,mH$$
بنابراین، اندوکتانس معادل مدار سلفی برابر با $$15\,mH$$ است.
جمع بندی
مشابه مقاومتها، سلفهای موازی نیز ولتاژ یکسانی دارند. همچنین، اندوکتانس معادل یک مجموعه موازی از سلفها، از اندوکتانس کوچکترین سلف آن مجموعه کوچکتر خواهد بود.
مشابه سلفهای سری، سلفهای موازی خاصیت القای متقابل دارند و بر اساس مقدار تزویج مغناطیسی بین آنها (که توسط پلاریته سلفها نشان داده میشود)، اندوکتانس معادلشان به نسبت حالت بدون القای مغناطیسی کم یا زیاد خواهد شد. بدین صورت که اگر سلفها پلاریته یکسان داشته باشند، القای متقابل به اندوکتانس معادل افزوده میشود و اگر پلاریته مخالف هم داشته باشند، القای متقابل از اندوکتانس معادل کم خواهد شد.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی برق
- آموزش ماشینهای الکتریکی 1
- مجموعه آموزشهای مهندسی قدرت
- آموزش الکترومغناطیس مهندسی
- مغناطیس چیست؟ — به زبان ساده
- مدارهای مغناطیسی — به زبان ساده
- آشنایی با ترانسفورماتورها — مجموعه مقالات جامع وبلاگ فرادرس
^^










واقعا سایتتون برا یادگیری عالیه