آزمون کندال W در آمار | پیاده سازی در SPSS
آزمون و روشهای ناپارامتری در آمار بسیار پر کاربرد هستند. در زمانی که اندازه نمونه کوچک بوده یا توزیع دادههای قابل تعیین نبوده و شرایط قضیه حد مرکزی برقرار نباشد، باید روشهای ناپارامتری آمار را به کار برد. در این نوشتار از مجله فرادرس به یک آزمون ناپارامتری به نام آزمون کندال W در آمار خواهیم پرداخت که برای دادههای ترتیبی و مقایسه چندین تیمار مناسب است. برای انجام محاسبات مربوطه نیز از نرمافزار محاسبات آماری SPSS کمک خواهیم گرفت.
برای آشنایی بیشتر با روشهای ناپارامتری و آزمون فرض، بهتر است نوشتارهای آمار پارامتری و ناپارامتری – انتخاب روش های تحلیل و آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات را مطالعه کنید. همچنین خواندن آزمون علامت (Sign Test) — به زبان ساده و آزمون فریدمن در SPSS | راهنمای کاربردی نیز خالی از لطف نیست.
آزمون کندال W در آمار
یکی از آزمونهای معروف در زمینه دادههای ترتیبی، آزمون کندال W است که توسط آمار شناس انگلیسی «موریس کندال» (Maurice Kendall) معرفی شد. او بوسیله آماره W، میزان همخوانی رتبهها را اندازهگیری کرد. واضح است که این آزمون برای «دادههای ترتیبی» (Ordinal) مناسب است.
آماره W کندال که به «ضریب توافق کندال» یا «ضریب همخوانی کندال» (Kendall's coefficient of concordance) نیز معروف است، یک آماره ناپارامتری است که نرمال شده «آزمون فریدمن» (Friedman Test) محسوب میشود. از این آماره و آزمون کندال W میتوان برای ارزیابی توافق یا سازگاری بین رأی دهندگان یا داورها استفاده کرد.
مقادیر آماره W کندال از صفر (به معنی عدم توافق) تا یک (به معنی توافق کامل) تغییر میکند. به عنوان مثال فرض کنید از تعدادی افراد جامعه، خواسته شده است تا به لیستی از مشغلههای ذهنی (از مهمترین تا کمترین اهمیت) رتبه بدهند. به این ترتیب با آزمون کندال W میتوان به این نتیجه رسید پاسخدهندگان نسبت به مشغلههای روزمره، توافق دارند یا خیر؟ در صورتی که باشد، تمامی پاسخدهندگان در اولویت مشغلههای ذهنی، اتفاق نظر داشتهاند و اگر باشد، ترتیب نگرانیهای آنها کاملا با یکدیگر فرق خواهد داشت و توافق بین پاسخ دهندگان وجود ندارد و حتی ممکن است پاسخهای آنها کاملاً تصادفی و از روی بیاطلاعی داده شده باشد.
نکته: واضح است هر چه مقدار W به یک نزدیک باشد، نشانگر توافق و هر چه به صفر نزدیک باشد، نمایانگر عدم توافق است.
در آزمونهای معمول برای سنجش وابستگی (وابستگی خطی) بین متغیرها، از «ضریب همبستگی پیرسون» (Pearson correlation coefficient) استفاده میشود که فرض نرمال بودن جامعههای آماری در آن نهفته است. از این شاخص اغلب برای نمایش رابطه خطی بین دو ویژگی دو جامعه بهره میبرند. در مقابل در آزمون کندال W هیچ فرضی راجع به ماهیت توزیع احتمال در نظر گرفته نمیشود و میتوان به تعداد دلخواه () تیمار یا جامعه را مورد بررسی قرار داد.
آماره و ناحیه بحرانی آزمون کندال W
فرض کنید آزمودنی دارای «رتبه» (Rank) برابر با است که اندیس نشانگر شماره داور است. از طرفی میدانیم که آزمودنی و دارو (تیمار) در مجموعه دادهها وجود دارد. مجموع همه رتبهها برای آزمودنی ام را نامیده و به صورت زیر محاسبه میکنیم.
میانگین رتبهها برای همه مشاهدات نیز بر طبق فرمول زیر حاصل میشود.
به منظور رسیدن به آماره کندال W، مجموع مربعات اختلاف رتبهها نسبت به میانگین را محاسبه کرده و آن را مطابق با رابطه زیر، مینامیم.
به این ترتیب آماره آزمون کندال W به صورت زیر تعریف و محاسبه خواهد شد.
واضح است که اگر همه داورها (تیمارها) یکسان رتبهبندی کرده باشند، ، برابر با ۱ و در صورتی که نتایج کاملا متناقض در آرای آنها وجود داشته باشد، صفر خواهد شد.
مثال ۱
جدول زیر را برای رتبه بندی دو داور روی سه تابلو نقاشی در نظر بگیرید. در اینجا میخواهیم مقدار را در حالتی که همه در رتبهبندی توافق دارند، مورد بررسی قرار دهیم.
| تابلو ۱ | تابلو ۲ | تابلو ۳ | |
| داور اول | 1 | 2 | 3 |
| داور دوم | 1 | 2 | 3 |
| مجموع رتبهها () | 2 | 4 | 6 |
به این ترتیب محاسبات طبق فرمولهای گفته شده به صورت زیر خواهد بود:
در نتیجه مقدار به صورت زیر محاسبه خواهد شد.
و مقدار برابر با ۱ حاصل میشود.
مثال ۲
این بار حالت عدم تفاهم در نظرات و آرا را در نظر میگیریم. به جدول زیر توجه کنید.
| تابلو ۱ | تابلو ۲ | تابلو ۳ | |
| داور اول | 1 | 2 | 3 |
| داور دوم | 3 | 2 | 1 |
| مجموع رتبهها () | 4 | 4 | 4 |
محاسبات گفته شده، این بار به صورت زیر در خواهند آمد.
در نتیجه مقدار به صورت زیر محاسبه خواهد شد.
واضح است که مقدار برابر با صفرشده و مشخص است که نتایج برای داور دوم کاملا عکس داور اول است، هر چند برای تابلو دوم یک نظر داشتهاند. در نتیجه به نظر میرسد که کاملا شانسی (یا بدون تخصص) تابلوها را ارزشگذاری کردهاند.
«کندال» و «گیبونس» (Gibbons) در کتابی که در سال ۱۹۹۰ به نام «روشهای همبستگی رتبهای» منتشر کردند، بین «ضریب همبستگی اسپیرمن» (Spearman's rank correlation coefficients) و کندال W رابطه زیر را اثبات کردند.
طرح بلوکهای ناقص
تا اینجا فرض بر این بود که طرح آزمایش مورد نظر در آزمون کندال W یک طرح متوازن و کامل است. به این معنی که همه تیمارها روی همه بلوکها اجرا شدهاند. ولی اگر طرح بلوکها کامل نباشد، شیوه محاسبه آماره آزمون کندال W متفاوت خواهد بود.
طرح بلوک نامتوازن را به صورت زیر در نظر بگیرید.
- هر داور (تیمار) به آزمودنی، رتبهای یکسان داده است. واضح است که .
- هر آزمودنی، دقیقا به تعداد بار، رتبهبندی شده است. .
- هر زوج از آزمودنیها با یکدیگر برای قضاوت در اختیار بعضی از داورها به تعداد بار قرار میگیرند. این مقدار برای همه زوجها ثابت بوده و بزرگتر از ۱ است.
چنین طرحی را به صورت نشان میدهند. به این ترتیب آماره آزمون کندال W به صورت زیر تعریف میشود.
اگر و باشد، طرح کامل بوده و رابطه بالا به آماره کندال W برای طرح کامل تبدیل میشود.
آماره کندال W برای رتبههای گرهدار
در بحث رتبههای مقادیر تکراری، نسبت دادن رتبه، با شیوههای مختلف مانند میانگین رتبه، رتبه حداقل، رتبه تصادفی و ... به کار میرود. اما در اینجا از رتبه میانگین برای آماره آزمون کندال W استفاده خواهیم کرد. وقتی رتبهها، گرهدار میشوند (رتبه برای مقادیر تکراری)، به هر یک از مقادیر میانگین رتبههای واقعی نسبت داده میشود.
البته اگر هیچ مقدار برابری (یا نظر یکسانی) وجود نداشته باشد، رتبههای تکراری نیز ایجاد نخواهد شد. البته این امر کمی غیر عادی خواهد بود. به عنوان مثال، مجموعه دادههای {80،76،34،80،73،80} را در نظر بگیرید. واضح است که مقدارهای 80 پس از مرتبسازی مجموعه داده از کوچک به بزرگ، در رتبههای ۴، 5 و 6 قرار میگیرند. از آنجایی که همگی آنها برابر هستند بهتر است که میانگین رتبهها یعنی {4،5،6} را به عنوان رتبه هر یک از آنها به کار ببریم. در نتیجه رتبه ۵ برای هر یک از مقدارهای ۸۰ در نظر گرفته میشود و مجموعه رتبهها به صورت {5،3،1،5،2،5} برای همه دادهها ساخته میشود.
در صورت وجود رتبه گرهدار مقدار آماره W، کاهش مییابد. با این حال، این کار، تغییر زیاد روی مقدار صدک آماره آزمون نخواهد داشت، مگر اینکه تعداد رتبههای گرهدار بسیار زیاد باشد. برای تصحیح رتبهها، از ضریب تصحیحی به شکل زیر استفاده خواهیم کرد.
بطوری که ، تعداد رتبههای گرهدار در گروه ام از رتبههای گرهدار است. از طرفی نیز تعداد گروههایی است که رتبههای گرهدار دارند. واضح است که بین ۱ تا n برای داور یا تیمار ام تغییر خواهد کرد.
بنابراین، ضریب تصحیح برای مجموعه رتبههای داور ام است. توجه داشته باشید که اگر هیچ گرهای در رتبهها وجود نداشته باشید، مقدار صفر خواهد بود.
با در نظر گرفتن عامل تصحیح رتبههای گرهدار آماره آزمون کندال W به صورت زیر در خواهد آمد.
که در آن مجموع رتبهها برای آزمودنی ام و نیز مجموعه مقادیر روی همه مجموعهٔ (تعداد داورها یا تیمارها) رتبهها است.
آزمونهای با معنایی
در صورتی که رتبهها، کامل باشند (رتبه گرهدار وجود نداشته باشد)، آماره مناسب برای آزمون کندال براساس فرض صفر (که نشانگر رتبههای تصادفی است) به صورت زیر خواهد بود.
که دارای توزیع کای ۲ (Chi-Squared) با درجه آزادی است. اگر رتبهها ناقص باشند، آنگاه آماره آزمون به صورت زیر در خواهد آمد.
که باز هم توزیع کای ۲ با درجه آزادی خواهد داشت.
«لژندر» (Legendre) توان آزمون کای ۲ و آزمون ترتیبها را به منظور مقایسه معنیداری آزمون کندال W با استفاده از شبیهسازی انجام داد که براساس شبیهسازی صورت گرفته، معلوم شد که آزمون کندال W به ازاء محافظهکارتر از آزمون ترتیبها (Permutation Testing) است.
از طرفی «ماروتزی» (Marozzi) آماره آزمون کندال W و کارهای لژندر را توسعه داد و یک آماره جدید در سال ۱۹۳۹، مطرح کرد که دارای توزیع F است.
درجه آزادی آماره به ترتیب و است. او این نتیجه را گرفت که برای های کوچک، استفاده از آماره مناسبتر است.
اگر میخواهید مفاهیم اولیه و همچنین کاربرد آزمونها و روشهای ناپارامتری در آمار را فرا بگیرید، بهتر است فیلم آموزشی که در ادامه معرفی شده را مشاهده کنید. این آموزش بخصوص برای کسانی که در حوزه مدیریت و حسابداری و همچنین بازاریابی فعالیت دارند، مفید خواهد بود.
- برای مشاهده فیلم آموزش آزمون آماری ناپارامتریک و اجرای آن با SPSS - ویژه مدیریت و علوم انسانی + اینجا کلیک کنید.
آزمون کندال W در SPSS
هر چند محاسبات مربوط به آماره آزمون کندال W ساده به نظر میرسد، ولی استفاده از نرمافزارهای محاسبات آماری بر دقت و سرعت عملیات میافزاید. در این بخش به بررسی نحوه اجرای آزمون کندال W در SPSS خواهیم پرداخت. البته ابتدا با یک مثال موضوع را آغاز میکنیم.
مقایسه نتایج داوری بین چند نوشابه گازدار با آزمون کندال W
مثال: شش نوع نوشیدنی گاز دار به پنج دارو برای سنجش مطلوبیت ارائه شده است. هر یک از آنها به هر نوشابه براساس میزان رضایت، امتیازی از ۱ تا ۶ میدهد. واضح است که هر چه عدد امتیاز بیشتر باشد، مطلوبیت بیشتر خواهد بود. مقدار امتیاز ۱ کمترین رتبه (Worst) و امتیاز ۶ بیشترین مطلوبیت (Best) را نشان میدهد.
این مجموعه داده در فایلی به نام colatest.sav در قالب فشرده از اینجا قابل دریافت است. واضح است که در صورت خارج کردن فایل از حالت فشرده به فایل اطلاعاتی SPSS دسترسی داشته و میتوانید آن را در این نرمافزار، بارگذاری کنید.
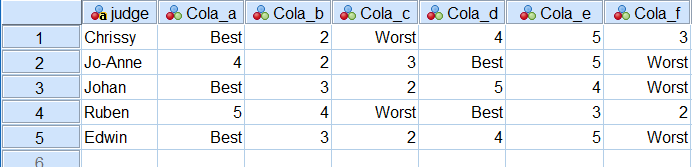
بهتر است ابتدا نگاهی به مجموعه دادهها بیاندازیم. در تصویر ۱، نمونهای از سطرهای این جدول اطلاعاتی را مشاهده میکنید. ستون اول، اسامی داورها و ستونهای بعدی امتیاز به نوشابهها است. هر ستون اختصاص به امتیاز یک نوشیدنی خاص دارد و سطرها، امتیاز داورها را برای آنها نشان میدهند.
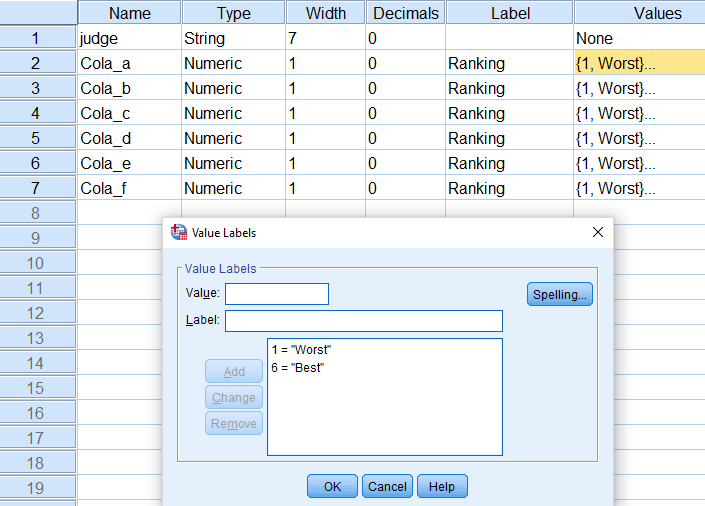
متغیرها و نوع هر یک از آنها نیز در تصویر ۲ دیده میشود. توجه داشته باشید که امتیازها از نوع «اسمی» (Nominal) هستند ولی رفتار ما با آنها به صورت دادههای «ترتیبی» (Ordinal) یا رتبهای خواهد بود. البته این موضوع در اجرای آزمون کندال تاثیری نخواهد گذاشت.
برای پاسخ به اینکه کدام نوشیدنی بهترین امتیاز را دارد، «آزمون فریدمن» (Friedman Test) مناسب خواهد بود، زیرا امتیازها به صورت رتبه بوده و تشکیل متغیرهای ترتیبی میدهند. ولی سوال اصلی ما این است که آیا همه داورها نسبت به میزان رضایت از نوشابهها، رفتار یکسانی دارند یا نه؟ در حقیقت اگر نظر داورها با یکدیگر مغایرت شدید داشته باشد، نمیتوانیم به نتایج ارزیابی نوشابهها، اعتماد داشته باشیم.
به این ترتیب میزان توافق آراء این داورها بر حسب آماره کندال W و همینطور آزمون مربوط به آن سنجیده میشود. در ادامه نحوه اجرای این آزمون در محیط SPSS را فرا خواهیم گرفت.
ولی قبل از شروع کار، بهتر است ایده اصلی در پس آماره آزمون کندال W را بیشتر درک کنیم. اجاره دهید در این قسمت، دو موقعیت فرضی را که در تصویر ۳، برای این مثال، نشان داده شده در نظر بگیریم: ۱- توافق کامل و ۲- اختلاف نظر کامل در بین رای داوران یا رای دهندگان.
نکته: محاسبات زیر در اکسل صورت گرفته است. جمع رتبهها برای هر دو حالت «کمترین توافق» و «بیشترین توافق» در سطر انتهایی (Column Total) محاسبه شده است.
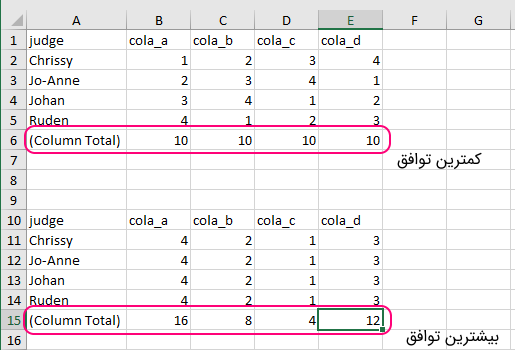
همانطور که میبینید، میزان توافق رای دهندگان با تفاوت در اختلاف ستونهای کل (Column Total) مشخص میشود. به این ترتیب میتوانیم میزان تفاوت در این اعداد را به عنوان یک شاخص یا آماره (مثل واریانس) بیان کنیم. طبق رابطهای که در قسمت قبل معرفی شد، شاخص آماری را به صورت زیر معرفی میکنیم.
صورت کسر نشانگر واریانس روی «جمع ستون» (Column Total) است و مخرج کسر نیز حداکثر واریانس ممکن براساس سطر جمع ستونها (Column Total) را نشان میدهد. در نتیجه، آماره آزمون کندال W همیشه بین 0 و 1 است. به عنوان مثال، نتیجه اختلاف نظر که در تصویر ۳ دیده میشود، با توجه به یکسان بوده مجموع آراء، باعث میشود که واریانس مقادیر سطر Column Total صفر شوده و در نتیجه آماره آزمون کندال W=0 بدست آید. اما در حالتی که توافق کامل بین آراء دیده میشود آماره W = 1 خواهد بود. زیرا واریانس در مجموع ستون با حداکثر واریانس ممکن برابر است.
نکته: مهم نیست که چگونه رتبه بندی را انجام میدهید (از بزرگ به کوچک یا کوچک به بزرگ)، بلکه مهم میزان پراکندگی بین رتبهها است.
کدی که در زیر مشاهده میکنید به منظور پیادهسازی آزمون کندال W در SPSS نوشته شده است.
1*Kendall's W from nonparametric tests - legacy dialogs - k related samples.
2
3NPAR TESTS
4/KENDALL=cola_a cola_b cola_c cola_d cola_e cola_f
5/MISSING LISTWISE.البته میتوانید از طریق فهرستها نیز به این دستور دسترسی پیدا کنید. مسیر مربوط به تصویر ۴ را طی کنید تا به پنجره K Related Samples برسید.
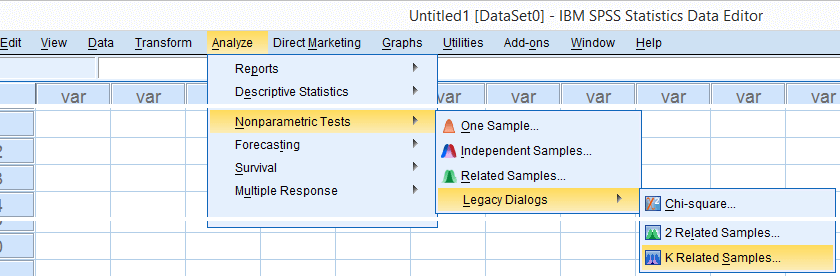
در تصویر ۵، تنظیمات و متغیرهایی که باید در بخش test Variables قرار گیرند، مشخص شدهاند. اگر می خواهید آزمون آماری با توزیع دقیق آماره W را به کار ببرید، از دکمه Exact استفاده کنید. در غیر اینصورت SPSS، آماره آزمون کندال W را با توزیع مجانبی برای فرض صفر در نظر میگیرد.
دکمه Statistics نیز برای درخواست آمارههایی نظیر میانگین و واریانس به کار میرود. البته ما هیچکدام از این گزینهها را به کار نبردهایم. ولی به طور پیشفرض، میانگین رتبهها محاسبه خواهد شد.
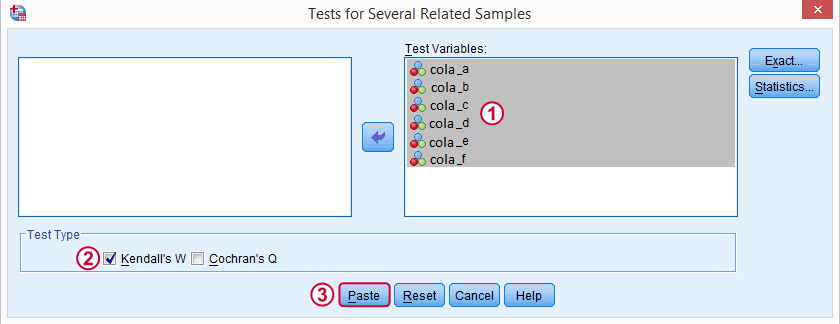
در صورتی که بخواهید کد این دستور را در پنجره Syntax ظاهر کنید، از دکمه Paste استفاده کنید. در غیر اینصورت به منظور اجرا، دکمه OK را انتخاب کنید. خروجیهای حاصل از اجرای این آزمون در ادامه قابل مشاهده هستند. البته برای هر یک از آنها نیز تفسیری یا توضیحی ارائه کردهایم.
خروجی و تفسیر نتایج آزمون کندال W
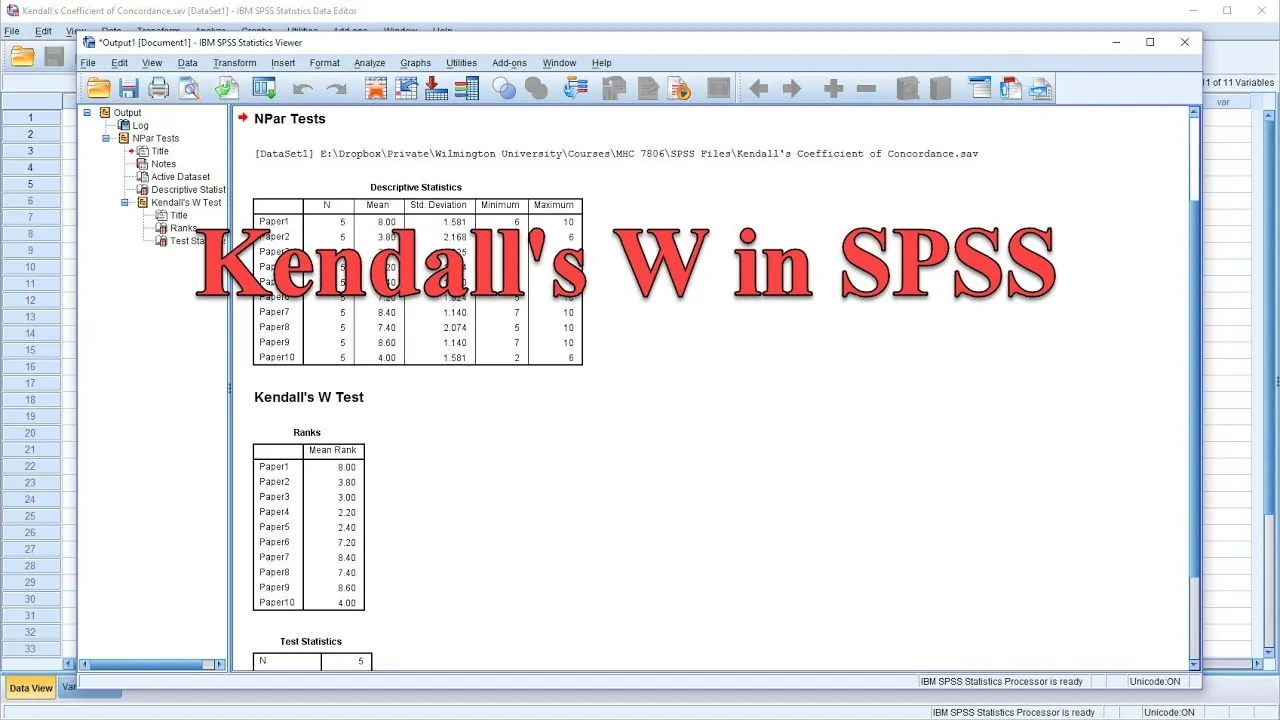
نتیجهای که پس از اجرای دستورات گفته شده، در پنجره خروجی Output نرمافزار SPSS ظاهر میشود، معرفی میانگین رتبهها است. این مقادیر را در ابتدای تصویر ۶ با عنوان Ranks مشاهده میکنید. با توجه به مقدار رتبهها، نوشابه A یا همان (cola_a) بیشترین میانگین رتبهها را دارد پس نسبت به دیگران دارای امتیاز رضایت بیشتری است. همچنین در ادامه نیز نتایج مربوط به محاسبه آماره آزمون کندال W دیده میشود.
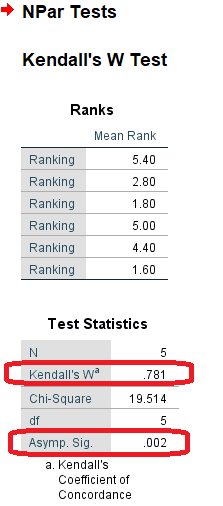
همانطور که مشخص است، مقدار آماره آزمون برابر با 781. بوده و از طرفی مقدار Sig یا همان مقدار احتمال (p value) کوچکتر از سطح آزمون مثلا ۰٫۰۵ است در نتیجه فرض صفر که تصادفی بودن (عدم تطابق) نتایج آراء در نظر گفته شده، رد خواهد شد. همچنین میبینید که مقدار آماره کای برای این آزمون ۱۹٫۵۱۴ است که از صدک 95ام این توزیع بزرگتر بوده. این نتایج، همگی به رد فرض صفر میانجامند.
میانگین همبستگی اسپیرمن
یکی دیگر از معیارهای اندازهگیری مطابقت، میانگینگیری روی «ضرایب همبستگی اسپیرمن» (Spearman Correlation Coefficient) است. همانطور که گفتیم بین آماره ازمون کندال و ضریب همبستگی اسپیرمن رابطه زیر برقرار است.
بطوری که میانگین همبستگی اسپیرمن و () تعداد داوران را نشان میدهد. به این ترتیب در مثال ما مقدار همبستگی اسپیرمن به صورت زیر محاسبه میشود و میتوان نتایج حاصل از داوریها را یکسان در نظر گرفت.
نکته: معمولا اگر ضریب همبستگی اسپیرمن بزرگتر از ۰٫۶ باشد، همبستگی را زیاد در نظر میگیریم.
معرفی فیلم آموزش آزمون آماری ناپارامتریک و اجرای آن با SPSS - ویژه مدیریت و علوم انسانی
هر چند روشهای پارامتری نسبت به روشهای ناپارامتری، بخصوص در آزمونهای آماری، توان بیشتری دارند ولی متاسفانه پیششرطهای استفاده از آنها در دادههای واقعی باعث میشود که نتوان به سادگی از آنها استفاده کرد. برای مثال فرض نرمال بودن جامعه آماری، یکی از فرضیههای مهم در به کارگیری روشهای پارامتری محسوب میشود که در جامعههای آماری واقعی کمتر به وقوع میپیوندد.
به همین دلیل در زمانی که توزیع قابل تشخیص نبوده یا تعداد مشاهدات و نمونه به اندازه کافی بزرگ نباشند، بهتر است از روشهای ناپارامتری که وابستگی کمتری به توزیع (بخصوص توزیع نرمال) دارند، استفاده شود.
در این فرادرس، مدرس سعی کرده است که هم هدف و شرایط اجرای آزمونهای ناپارامتری را شرح داده و هم چگونگی اجرای آن را در محیط نرم افزار SPSS، آموزش دهد. در این بین با ذکر بعضی از مثالها، محاسبات به صورت دستی و همچنین با نرمافزار اجرا خواهند شد.
این فرادرس شامل چهار ساعت و هفت دقیقه، فیلم آموزشی است که در قالب یازده درس ارائه میشود. فهرست عناوین این درسها در ادامه آورده شدهاند.
- درس یکم: بررسی آزمون های پارامتریک و ناپارامتریک و تفاوت آنها
- درس دوم: آزمون علامت یک نمونهای به همراه اجرا در محیط SPSS
- درس سوم: آزمون علامت زوج نمونه ای و اجرا در نرمافزار SPSS
- درس چهارم: آزمون رتبه علامت دار یا ویلکاکسون (Wilcoxon) در SPSS
- درس پنجم: آزمون های مجموع رتبه ها، شامل آزمون U (ویلکاکسون، یو من ویتنی) و آزمون H (کروسکال - والیس) به همراه اجرای این آزمونها در محیط SPSS
- درس ششم: آزمون مبتنی بر ردیفها
- درس هفتم: ضریب همبستگی ناپارامتری رتبهای اسپیرمن و محاسبه آن در SPSS
- درس هشتم: آزمون کولموگروف - اسمیرنوف (Kolmogorov–Smirnov) به منظور آزمون یکویی برازش در SPSS
- درس نهم: آزمون فریدمن (Friedman Test) برای مقایسه چندین جامعه مستقل در SPSS
- درس دهم: آزمون مک - نمار (McNemar's Test) در جدول توافقی
- درس یازدهم: آزمون کوکران (Cochran Test) و کاربرد آن در تحلیل دادههای دو وضعیتی
این آموزش بخصوص برای کسانی که در حوزههای مدیریت، حسابداری، روانشناسی، آمار، علوم اجتماعی، علوم سیاسی و علوم تربیتی به تحقیق میپردازند، مفید خواهد بود. برای درک بهتر و سرعت در فراگیری مطالب این آموزش، آشنایی با محیط نرمافزار اکسل و همچنین کار با نرم افزار SPSS، به همراه آشنایی با آمار و آزمونهای آماری لازم و ضروری است.
- برای مشاهده فیلم آموزش آزمون آماری ناپارامتریک و اجرای آن با SPSS - ویژه مدیریت و علوم انسانی + اینجا کلیک کنید.
خلاصه و جمعبندی
در این نوشتار به بررسی روش محاسبه آماره و اجرای آزمون ناپارامتری کندال W پرداخته محاسبات و نتایج حاصل از اجرای آن را در خروجیهای مربوط به نرمافزار SPSS تفسیر کردیم. همانطور که گفته شد، این آزمون به منظور سازگاری چندین تیمار روی دادههای ترتیبی کاربرد دارد. در نتیجه اگر میخواهید توافق نتایج یک داوری یا قضاوت که براساس رتبهبندی صورت گرفته است را ارزیابی کنید، آزمون کندال W گزینه مناسبی خواهد بود.














با درود و آرزوی سلامتی،
آقای دکتر آرمان ریبد درک بسیار خوبی از آمار دارند و در حد خلاصه نویسی، کار عالیست.
با احترام،
مقدم.
با سلام و وقت به خیر
خیلی ممنونم از آموزش های خوبتون. سوالی از حضورتدن داشتم:
چنانچه رتبه گره دار داشتیم چگونه در اس پس اس اس از آزمون کندال دبلیو استفاده کنیم؟