وتر چیست؟ — به زبان ساده

در آموزش‌های قبلی مجله فرادرس، با دو شکل هندسی دایره و مثلث آشنا شدیم. اگر با این شکل‌ها سر و کار داشته باشید، احتمالاً واژه وتر را نیز خواهید شنید که برای این دو شکل هندسی به کار می‌رود. در این آموزش، با وتر در دایره و وتر در مثلث آشنا می‌شویم.

وتر دایره

«وتر» (Chord) دایره پاره‌خطی است که دو نقطه روی محیط دایره را به هم وصل می‌کند.

فیلم آموزش ریاضی پایه هفتم – جامع و با نکات مهم در فرادرس

کلیک کنید

بنابراین، می‌توان گفت که هر دایره بی‌نهایت و‌تر دارد. جالب است بدانید که قطر بلندترین و‌تر دایره است که از مرکز آن عبور می‌کند. شکل زیر یک دایره و دو و‌تر‌ و یک شعاع آن را نشان می‌دهد.

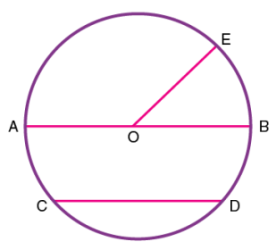
در دایره شکل بالا با مرکز O، پاره‌خط AB قطر دایره (طولانی‌ترین وتر)، OE شعاع دایره و CD و‌تر دایره است.

اکنون دایره شکل زیر را در نظر بگیرید. فرض کنید CD وتر دایره بوده و دو نقطه P و Q را هر جایی روی محیط دایره مشخص کنیم.

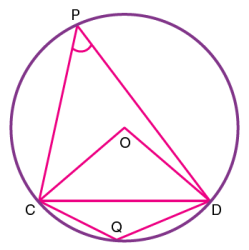
اگر نقاط انتهایی وتر CD را به نقطه P وصل کنیم، آنگاه زاویه $$\angle CPD$$ به عنوان زاویه مقابل به و‌تر شناخته می‌شود. همچنین، زاویه $$\angle CQD$$ زاویه مقابل به وتر در نقطه Q است. زاویه $$\angle COD$$ نیز زاویه مقابل به و‌تر CD است که در مرکز O قرار گرفته است.

• مطالب پیشنهادی برای مطالعه:
  • عدد پی (Π) چیست؟ — کاربردها به زبان ساده
  • نسبت محیط دایره به قطر آن چیست؟ — به زبان ساده
  • شعاع چیست؟ — شعاع دایره به زبان ساده (+ فیلم آموزش رایگان)
  • نسبت محیط دایره به شعاع آن چیست؟ — به زبان ساده
  • دایره چند شعاع دارد؟ — تصویری و به زبان ساده

فرمول طول وتر دایره

شکل زیر را در نظر بگیرید.

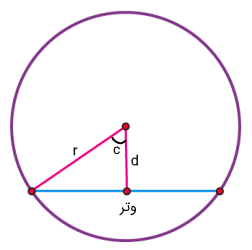
دو فرمول اصلی برای یافتن طول وتر یک دایره وجود دارد:

• با داشتن فاصله عمودی وتر از مرکز دایره، طول وتر‌ برابر است با:

$$\large 2 \times \sqrt {r^2-d^2}$$ = طول وتر

• اگر $$\angle c$$ نصف زاویه مقابل به وتر باشد، طول وتر‌ به صورت زیر به دست می‌آید:

$$\large 2 \times r \times \sin (c)$$ = طول وتر

در فرمول‌های بالا، $$r$$‌ شعاع دایره، $$d$$ فاصله عمودی وتر تا مرکز دایره و $$c$$ زاویه بین شعاع و خط عمود است.

چند قضیه درباره وتر دایره

در این بخش، چند قضیه معروف را درباره وترِ دایره بیان می‌کنیم.

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

قضیه ۱: وترهایی که طول آن‌ها برابر است، زاویه‌های مقابل آن‌ها که در مرکز قرار دارند، با هم برابر هستند.

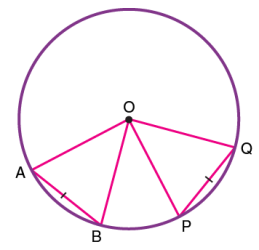
قضیه ۲: وترهایی که زاویه مقابل آن‌ها در مرکز بوده و اندازه این زاویه‌ها مساوی است، دارای طول برابری هستند.

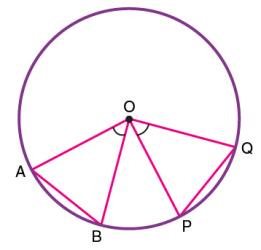
قضیه ۳:‌ وترهای برابر در یک دایره، فاصله یکسانی تا مرکز دایره دارند. یعنی اگر AB برابر با CD باشد، OP و OQ برابر خواهند بود.

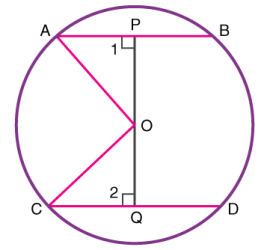
قضیه 4: خطی که از مرکز دایره تا نقطه میانی وتر رسم می‌شود، عمود بر آن است. به عبارت دیگر، هر خط از مرکز دایره که وتر را به دو قسمت مساوی تقسیم کند، عمود بر آن است. عکس این قضیه نیز برقرار است.

قضیه 5: اگر سه نقطه غیرهم‌خط وجود داشته باشد، فقط یک دایره وجود دارد که می‌تواند از آن‌ها عبور کند.

قضیه ۶: وترهایی با فاصله یکسان از مرکز یک دایره دارای طول برابر هستند.

• مطالب پیشنهادی برای مطالعه:
  • قطاع و مقطع دایره و محاسبات آن در هندسه — به زبان ساده + فیلم آموزش رایگان
  • محیط نیم دایره چیست؟ — به زبان ساده + حل تمرین و مثال
  • مساحت نیم دایره چگونه بدست می‌آید؟ — به زبان ساده + حل مثال
  • محیط ربع دایره چیست؟ — به زبان ساده + حل تمرین و مثال
  • مساحت ربع دایره چیست؟ — به زبان ساده + حل تمرین و مثال

مثال‌های وتر دایره

در این بخش چند مثال را بررسی می‌کنیم.

فیلم آموزش هندسه پایه دهم – هندسه 1 در فرادرس

کلیک کنید

مثال اول وتر دایره

فاصله وتر دایره‌ای تا مرکز آن، برابر با ۴ سانتی‌متر و شعاع دایره ۷ سانتی‌متر است. طول وتر آن دایره را پیدا کنید.

حل: طول شعاع $$r = 7\; \text{cm}$$ و فاصله عمودی $$d = 4 \; \text{cm}$$ وتر تا مرکز دایره را داریم. طبق فرمولی که بیان کردیم، طول وتر به صورت زیر به دست می‌آید:

$$\large 2 \times \sqrt {r^2-d^2} = 2\sqrt{7^2-4^2 }=2\sqrt{49-16}\\ \large =2\sqrt{33} = 2\times 5.744 = 11.48 \; \text{cm}$$

مثال دوم وتر دایره

شعاع، قطر و وتر دایره زیر را مشخص کنید.

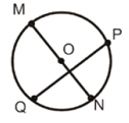
حل: MN و PQ وترهای دایره هستند. وترِ MN که از مرکز دایره عبور کرده و بزرگ‌ترین وتر دایره است، قطر دایره نیز هست. همچنین، ON و OM شعاع‌های دایره هستند.

مثال سوم وتر دایره

در شکل زیر، اگر اندازه وتر PQ برابر با ۱۰ واحد باشد، اندازه پاره‌خط PA چقدر است؟

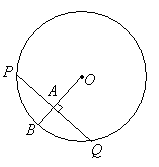
حل: همان‌طور که در شکل می‌بینیم، OB عمود بر PQ است. بنابراین، طبق قضایایی که در بالا گفتیم (قضیه ۴)، اندازه PA نصف PQ، یعنی ۵ واحد است.

وتر مثلث

در مثلث قائم‌الزاویه، وتر‌ به جای واژه انگلیسیِ Hypotenuse به کار می‌رود. ‌وتر طولانی‌ترین ضلع مثلث قائم‌الزاویه است. این ضلع روبه‌روی زاویه قائم (90 درجه) است.

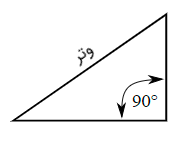
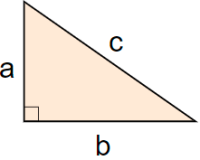
طول وتر مثلث قائم‌الزاویه را می‌توان با استفاده از قضیه فیثاغورس به دست آورد.‌ در مثلث قائم‌الزاویه زیر، وتر طبق قضیه فیثاغورس برابر است با:

$$\large c = \sqrt{a^2 + b^2 }$$