فرادرسقضیه تونن (Thevenin’s Theorem) — مفاهیم کلیدی (+ دانلود فیلم آموزش رایگان)
در آموزش‌های قبل دیدیم که می‌توان مدارهای الکتریکی پیچیده را با قوانین مداری کیرشهف (KVL و KCL)، تحلیل مش و تحلیل گره حل کرد. اما علاوه بر این روش‌ها، قضایای تحلیل مداری وجود دارند که با استفاده از آن‌ها می‌توان جریان و ولتاژ هر نقطه‌ای از مدار را محاسبه کرد. در این آموزش، «قضیه تونن» (Thevenin’s Theorem) را معرفی می‌کنیم که یکی از مهم‌ترین قضایای تحلیل مدار است.
قضیه تونن بیان می‌کند: «هر مدار خطی متشکل از منابع ولتاژ و مقاومت‌ها را می‌توان با یک منبع ولتاژ با مقاومت سری با آن جایگزین کرد». به عبارت دیگر، می‌توان هر مدار الکتریکی را بدون توجه به میزان پیچیدگی، با یک مدار دو سر شامل منبع ولتاژ و مقاومت یا امپدانس سری با آن ساده کرد. شکل زیر این موضوع را به خوبی نشان می‌دهد.
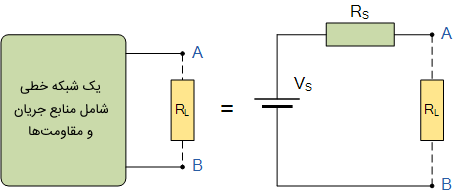
قضیه تونن، خصوصاً برای معادل‌سازی سیستم‌های شامل باتری و مدارهای مقاومتی متصل به آن‌ها مناسب است.
برای بررسی مدار از دو سر مقاومت $$R_L$$، شبکه تک قطبی شامل عناصر مقاومتی و منابع انرژی را می‌توان با مقاومت معادل Rs و ولتاژ معادل Vs جایگزین کرد. مقاومت Rs مقدار مقاومت منبع از دید دوسر خروجی مدار و Vs مقدار ولتاژ مدار باز است.
مدار شکل زیر را در نظر بگیرید. می‌خواهیم مدار معادل تونن را از دو سر A و B محاسبه کنیم.
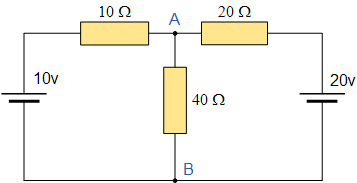
محاسبه مقاومت معادل
برای تحلیل مدار، ابتدا فرض می‌کنیم مقاومت بین دو سر A و B وجود نداشته باشد و آن را مدار باز می‌کنیم. سپس برای محاسبه مقاومت معادل، منابع ولتاژ را اتصال کوتاه می‌کنیم (منابع جریان را مدار باز می‌کنیم).
اکنون، مقاومت معادل را می‌توان با محاسبه مقاومت کل دیده شده از دو سر A و B به دست آورد. شکل زیر، تغییرات مدار را برای محاسبه مقاومت معادل نشان می‌دهد.
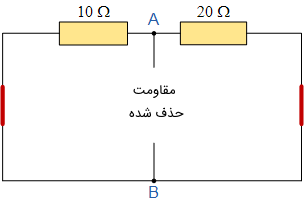
با توجه به شکل بالا، دو مقاومت 10 و 20 اهمی موازی می‌شوند و معادل آن‌ها طبق رابطه زیر به دست می‌آید:
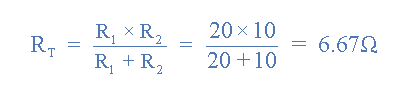
محاسبه ولتاژ معادل
ولتاژ Vs، برابر با کل ولتاژی است که هنگام مدار باز بودن A و B (یعنی مقاومت $$R_L$$ را از مدار جدا کنیم)، بین آن‌ها می‌افتد.
در این حالت، منابع در مدار حضور دارند. با کمک شکل زیر، این ولتاژ را محاسبه می‌کنیم.
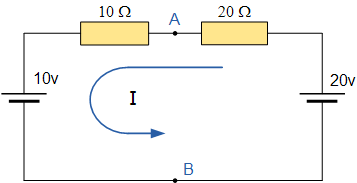
جریان حلقه مدار با عبارت زیر قابل محاسبه است:
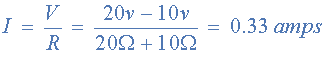
این مقدار جریان، از هر دو مقاومت می‌گذرد، بنابراین می‌توان ولتاژ $$V_{AB}$$ را به صورت زیر به دست آورد:
$$V_{AB}=20-(20\Omega\times0.33A)=13.33V$$
یا
$$V_{AB}=10+(10\Omega\times0.33A)=13.33V$$
در نهایت، مدار معادل تونن متشکل از منبع ولتاژ 13.33 ولتی و مقاومت 6.67 اهمی به صورت زیر به دست می‌آید.
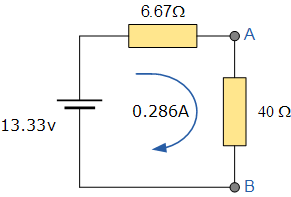
جریان مدار معادل با رابطه ساده زیر محاسبه می‌شود:
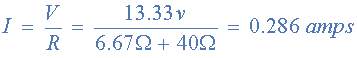
که برابر با مقداری است که با استفاده از قانون مداری کیرشهف به دست آوردیم.
مدار معادل تونن ترانزیستورها، منابع ولتاژ مانند باتری‌ها و غیره در طراحی مدار بسیار مهم است.
جمع‌بندی
دیدیم که قضیه تونن، یکی دیگر از ابزارهای تحلیل مدار است که برای کاهش مدارهای پیچیده به یک مدار ساده (شامل یک منبع ولتاژ و یک مقاومت) استفاده می‌شود. اگر از دو ترمینال A و B به مدار نگاه کنیم، مدار معادل دقیقاً مانند مدار اصلی عمل می‌کند و رابطه i-v از دو سر A و B در دو حالت مشابه است.
روند اصلی حل معادله با کمک قضیه تونن را می‌توان به صورت زیر خلاصه کرد:
- مقاومت بار $$R_L$$ یا عنصر دیگر مدار را که در نظر دارید، از مدار حذف کنید.
- مقاومت $$R_S$$ را با اتصال کوتاه کردن منابع ولتاژ و مدار باز کردن منابع جریان محاسبه کنید.
- ولتاژ $$V_S$$ را با یکی از روش‌های تحلیل مدار بیابید.
- جریان مقاومت بار $$R_L$$ را محاسبه کنید.
در آموزش بعدی، مدار معادل نورتن را معرفی می‌کنیم که مدار را در یک منبع جریان موازی با مقاومت خلاصه می‌کند.
اگر مطالب بیان شده برای شما مفید بوده و می‌خواهید درباره موضوعات مرتبط با آن بیشتر بدانید، پیشنهاد می‌کنیم به آموزش‌های زیر مراجعه کنید:
^^
فیلم های آموزش قضیه تونن (Thevenin’s Theorem) — مفاهیم کلیدی (+ دانلود فیلم آموزش رایگان)
فیلم آموزشی قضیه تونن
فیلم آموزشی حل مثال از قضیه تونن و روش سریع محاسبه مدار معادل
خیلی کامل و ساده
تشکر
خیلی عالی
ایزد یکتا نگهدارتون باشه
سپاس
بسیار کوتاه, مختصر و مفید بود.
ممنونم از شما.
سلام.
خوشحالیم که این آموزش برایتان مفید بوده است.
شاد و پیروز باشید.
خیلی جامع و مفید و کامل توضیح داده شده.
سلام.
خوشحالیم که این آموزش برایتان مفید بوده است.
شاد و پیروز باشید.