مکانیک شکست الاستیک خطی — مفاهیم، روابط و کاربردها

«مکانیک شکست» (Fracture Mechanics)، یکی از شاخه‌های علم مکانیک است که به مطالعه مکانیسم رشد ترک در مواد مختلف می‌پردازد. در مکانیک شکست، از روش‌های تحلیل مکانیک جامدات برای محاسبه نیروهای محرک اعمال شده بر ترک و از روش‌های تجربی برای تعیین مقاومت ماده در برابر شکست استفاده می‌شود.

امروزه در علم مواد، مکانیک شکست به عنوان یک ابزار مهم برای بهبود عملکرد قطعات مکانیکی به حساب می‌آید. مکانیک شکست با اعمال قوانین فیزیکی تنش و کرنش (بخصوص تئوری‌های الاستیسیته و پلاستیسیته) به عیب و نقص‌های ساختار بلوری مواد در مقیاس میکروسکوپی، رفتار مکانیکی آن‌ها در مقیاس ماکروسکوپی را پیش‌بینی می‌کند. «شکست‌نگاری» (Fractography)، یکی از علوم پرکاربرد در این حوزه است که به منظور ارزیابی دلایل شکست و اعتبارسنجی پیش‌بینی‌های تئوری شکست با شکست‌های واقعی مورد استفاده قرار می‌گیرد. پیش‌بینی رشد ترک یکی از مؤلفه‌های اصلی بررسی «تحمل آسیب» (Damage Tolerance) در اصول طراحی مکانیکی محسوب می‌شود.

به طور کلی، مکانیک شکست به دو بخش «مکانیک شکست الاستیک خطی» (Linear Elastic Fracture Mechanics) و «مکانیک شکست الاستیک-پلاستیک» (Elastic–Plastic Fracture Mechanics) تقسیم‌بندی می‌شود. در این مقاله شما را با مفاهیم، روابط و کاربردهای مکانیک شکست الاستیک خطی آشنا خواهیم کرد.

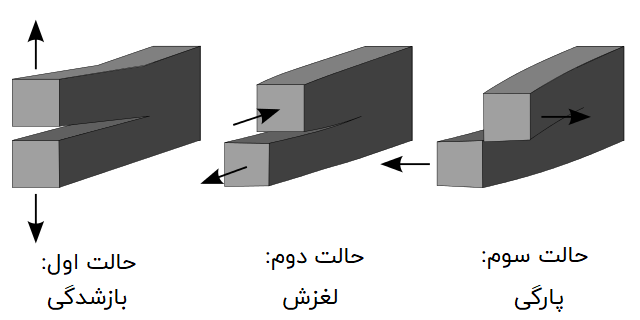
به طور کلی، سه حالت برای شروع رشد ترک وجود دارد:

• ترک حالت اول (Mode I): حالت بازشدگی (ناشی از تنش کششی عمود بر سطح ترک)
• ترک حالت دوم (Mode II): حالت لغزش (ناشی از اعمال یک تنش برشی موازی با سطح ترک و عمود بر بخش جلویی ترک)
• ترک حالت سوم (Mode III): حالت پارگی (ناشی از اعمال تنش برشی موازی با سطح ترک و همچنین موازی با بخش جلویی ترک)

اهمیت مکانیک شکست

عمر مکانیک شکست به کمتر از 100 سال می‌رسد و علم نسبتاً جدیدی به حساب می‌آید. فرآیندهای ساخت، تولید، ماشین‌کاری و شکل‌دهی مواد می‌توانند منجر به ایجاد عیب و نقص‌هایی در قطعات مکانیکی شوند. در فرآیند ساختِ تمام قطعات فلزی، عیب و نقص‌های داخلی و سطحی قابل مشاهده هستند. باید توجه داشت که تمام این عیب و نقص‌ها در هنگام به کارگیری ناپایدار نخواهند بود.

مکانیک شکست روشی است که تحلیل عیب و نقص‌های یک قطعه به منظور شناسایی ترک‌های ایمن (بدون احتمال رشد) و ترک‌های مستعد رشد را امکان‌پذیر می‌کند. ترک‌های مستعد رشد می‌توانند باعث رخ دادن شکست در یک قطعه یا سازه شوند. علیرغم وجود عیب و نقص‌های ذاتی یک سازه، امکان دستیابی به نتایج ایمن در تحلیل تحمل آسیب وجود دارد (وجود عیب و نقص دلیل کافی برای رخ دادن شکست نیست).

اهداف مکانیک شکست

هدف اصلی مکانیک شکست، ارائه پاسخ‌های کمی برای سؤالات زیر است:

• اگر یک قطعه را تابعی از اندازه ترک‌ها در نظر بگیریم، مقاومت آن چقدر خواهد بود؟
• اندازه ترک‌ها باید چقدر باشد تا قطعه تحت شرایط بارگذاری عملیاتی دوام بیاورد؟ به عبارت دیگر، حداکثر اندازه مجاز برای ترک‌ها چقدر است؟
• با در نظر گرفتن یک اندازه اولیه مشخص برای ترک، مدت زمان لازم برای رشد و گسترش آن چقدر خواهد بود؟ به عبارت دیگر، حداقل اندازه قابل شناسایی ترک و حداکثر اندازه مجاز ترک چقدر است؟
• اگر فرض کنیم که یک سازه قبل از به کارگیری دارای عیب و نقص‌هایی با اندازه مشخص باشد (مانند عیب‌های ناشی از فرآیند تولید)، میزان عمر سرویس‌دهی آن چقدر خواهد بود؟
• در طی مدت زمان قابل دسترس برای شناسایی ترک‌ها، هرچند وقت یکبار باید سازه را از نظر وجود ترک مورد بازرسی قرار دارد؟

مکانیک شکست الاستیک خطی

مکانیک شکست الاستیک خطی به منظور تخمین مقدار انرژی مورد نیاز برای گسترش‌ها ترک‌های موجود در یک ماده شکننده مورد استفاده قرار می‌گیرد. در ادامه به معرفی رویکردهای پرکاربرد در این حوزه می‌پردازیم.

معیار گریفیث

مکانیک شکست در طی جنگ جهانی اول توسط «آلن آرنولد گریفیث» (Alan Arnold Griffith)، یک مهندس هوافضای انگلیسی، به منظور توصیف ساز و کار شکست مواد شکننده توسعه یافت. گریفیث شروع مطالعات خود بر روی مکانیک شکست را از دو واقعیت متناقض زیر الهام گرفت:

• تنش مورد نیاز برای ایجاد شکست در یک شیشه، 100 مگا پاسکال (MPa) است.
• تنش تئوری مورد نیاز برای شکستن پیوند اتمی درون یک شیشه، 10000 مگا پاسکال است.

گریفیث احساس کرد که توجیه این مشاهدات متناقض به معرفی یک تئوری جدید نیاز دارد. علاوه بر این، بر اساس آزمایش‌های صورت گرفته توسط او بر روی الیاف شیشه، نشان داده شد که با کاهش قطر الیاف، تنش مورد نیاز برای ایجاد شکست افزایش می‌یابد. از این‌رو، مقاومت کششی تک‌محوری (پارامتری پرکاربرد در پیش‌بینی شکست مواد پیش از ارائه معیار گریفیث) نمی‌توانست به عنوان یک ویژگی مستقل از مشخصات نمونه آزمایشگاهی در نظر گرفته شود. گریفیث بیان کرد که کم بودن مقاومت شکست مشاهده شده در آزمایش‌ها و همچنین وابستگی این مقاومت به اندازه نمونه، به حضور نقص‌ها و ترک‌های میکروسکوپی درون ماده مربوط می‌شود.

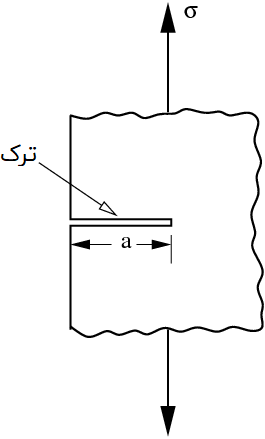
گریفیث برای تأیید فرضیه تأثیر ترک‌ها بر روی مقاومت ماده، یک ترک مصنوعی بر روی نمونه‌های شیشه ایجاد کرد. این ترک مصنوعی به صورت سطحی و بسیار بلندتر از دیگر ترک‌های نمونه بود. آزمایش‌ها نشان دادند که حاصل‌ضرب جذر طول ترک در تنش شکست نمونه، یک مقدار تقریباً ثابت است:

a: طول ترک؛ σ_f: تنش در لحظه شکست؛ C: ثابت عددی

توجیه این رابطه با توجه به تئوری الاستیسیته خطی دشوار است. بر اساس تئوری الاستیسیته خطی، تنش و کرنش پیش‌بینی شده روی نوک یک ترک نوک‌تیز در مواد الاستیک خطی، بی‌نهایت خواهد بود. گریفیث به منظور برطرف کردن این مشکل، یک رویکرد ترمودینامیک را برای توصیف رابطه مشاهده شده توسعه داد.

برای رشد یک ترک و گسترش سطوح آن از هر دو طرف باید انرژی سطحی به اندازه کافی افزایش یافته باشد. گریفیث با حل مسئله الاستیسیته یک ترک محدود در یک صفحه الاستیک، رابطه‌ای را برای تعیین ثابت C با توجه به انرژی سطحی ترک به دست آورد. مراحل انجام رویکرد اتخاذ شده برای این محاسبات به صورت زیر خلاصه می‌شوند:

• محاسبه انرژی پتانسیل ذخیره شده در یک نمونه کامل تحت بارگذاری کششی تک‌محوری
• فیکس کردن مرزهای نمونه برای جلوگیری ایجاد ترک بر اثر اعمال بار - وجود ترک باعث رهاسازی تنش و کاهش انرژی الاستیک در نزدیکی سطوح ترک می‌شود. از طرف دیگر، ترک انرژی سطحی کلی نمونه را افزایش می‌دهد.
• محاسبه تغییرات انرژی آزاد (انرژی سطحی – انرژی الاستیک) به عنوان تابعی از طول ترک - شکست هنگامی رخ می‌دهد که انرژی آزاد به مقدار حداکثری خود در طول بحرانی ترک برسد. با افزایش طول ترک پس از این مقدار حداکثری، انرژی آزاد کاهش خواهد یافت.

گریفیث با در نظر گرفتن مراحل محاسباتی بالا به رابطه زیر دست یافت:

E: مدول یانگ؛ γ: چگالی انرژی سطحی ماده

گریفیث با در نظر گرفتن مقدار 62 گیگا پاسکال برای مدول یانگ و مقدار 1 ژول بر مترمربع (J/m²) برای چگالی انرژی سطحی، مطابقت بسیار خوبی را بین تنش پیش‌بینی شده شکست و تنش آزمایشگاهی شکست برای یک نمونه شیشه مشاهده کرد.

معیار گریفیث توسط «جانسون» (Johnson)، «کندال» (Kendall) و «رابرتس» (Roberts) برای مسائل مربوط به سطوح چسبنده نیز مورد استفاده قرار گرفته است. نتایج یک تحقیق صورت گرفته توسط «پوپوف» (Popof) در سال 2017 نمایش داد که به کارگیری مستقیم معیار گریفیث در یک سلول عددی، امکان دستیابی به یک رابطه بسیار قدرتمند برای روش المان مرزی را فراهم می‌کند.

اصلاحات اروین

تا اوایل دهه 1950 میلادی، مطالعات گریفیث توسط گروه بزرگی از مهندسان نادیده گرفته می‌شد. این مسئله دو دلیل کلی داشت:

1. برای مواد واقعی مورد استفاده در سازه‌ها، مرتبه بزرگی سطح انرژی مورد نیاز برای ایجاد شکست نسبت به انرژی سطحی بزرگ‌تر است.
2. در این‌گونه مواد همیشه مقداری تغییر شکل غیر الاستیک در بخش جلویی ترک وجود دارد که فرض محیط الاستیک خطی به همراه تنش‌های بی‌نهایت در نوک ترک را به کلی رد می‌کند.

تئوری گریفیث با داده‌های تجربی به دست آمده از آزمایش بر روی مواد شکننده‌ای نظیر شیشه مطابقت بسیار خوبی دارد. اگرچه برای مواد شکل‌پذیری مانند فولاد، مقدار انرژی سطحی پیش‌بینی شده توسط این تئوری معمولاً بسیار بزرگ است. به همین دلیل برای این‌گونه مواد از رابطه زیر استفاده می‌شود:

در طی جنگ جهانی دوم، گروهی از دانشمندان آزمایشگاه تحقیقاتی وابسته به نیروی دریایی ایالات متحده به سرپرستی «جورج رنکین اروین» (George Rankine Irwin)، دریافتند که خاصیت پلاستیسیته نقش بسیار مهمی را در شکست مواد شکننده بازی می‌کند.

در مواد شکل‌پذیر (حتی مواردی که شکننده به نظر می‌رسند)، یک ناحیه پلاستیک در نوک ترک توسعه می‌یابد (تصویر زیر). با افزایش بارگذاری، اندازه این ناحیه بزرگ‌تر می‌شود. این افزایش اندازه تا هنگام رشد ترک و تخلیه مواد تحت کشش الاستیک در پشت نوک ترک ادامه خواهد داشت. چرخه بارگذاری و باربرداری پلاستیک در نزدیکی نوک ترک باعث اتلاف انرژی به صورت حرارت می‌شود. بنابراین، به منظور تعدیل انرژی در معادله گریفیث برای مواد شکننده باید عبارتی برای بیان اتلاف انرژی اضافه می‌شد.

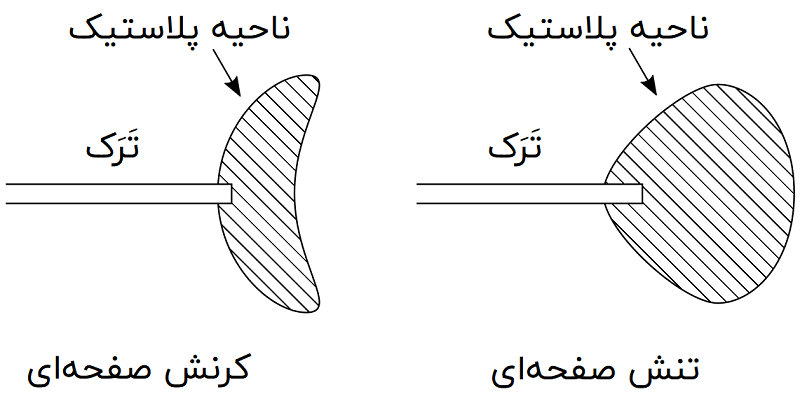
در رویکرد اروین، انرژی به دو بخش زیر تقسیم می‌شود:

• بخش اول: انرژی کرنش الاستیک ذخیره شده که با رشد ترک تخلیه می‌شود. این بخش، نیروی محرک ترمودینامیک برای ایجاد شکست است.
• بخش دوم: انرژی اتلاف شده که شامل اتلاف انرژی پلاستیک و انرژی سطحی می‌شود. این انرژی اتلاف شده، مقاومت ترمودینامیک در برابر شکست را فراهم می‌کند.

با توجه به موارد بالا، رابطه انرژی کل به صورت زیر خواهد بود:

γ: انرژی سطحی؛ G_p: اتلاف انرژی پلاستیک بر واحد مساحت رشد ترک

با توجه به رابطه بالا، فرم اصلاح شده معیار انرژی گریفیث به صورت زیر نوشته خواهد شد:

برای مواد شکننده‌ای نظیر شیشه، انرژی سطحی بر اتلاف انرژی غلبه می‌کند (2γ≈G). در نتیجه مقدار انرژی کل تقریباً برابر 2 ژول بر مترمربع خواهد بود. در مواد شکل‌پذیری مانند فولاد، اتلاف انرژی پلاستیک پارامتر غالب بوده (G_p≈G) و انرژی کل تقریباً برابر 1000 ژول بر مترمربع است. برای پلیمرهایی با دمای نزدیک به دمای انتقال شیشه، مقدار انرژی کل بین 2 تا 1000 ژول بر مترمربع تغییر می‌کند.

ضریب شدت تنش

یکی دیگر از دستاوردهای مهم اروین و همکارانش، یافتن روشی برای محاسبه مقدار انرژی قابل دسترس شکست با توجه به تنش مجانبی و میدان‌های جابجایی اطراف بخش جلویی ترک در یک جامد الاستیک خطی بود. رابطه بین عبارت مجانبی تنش نرمال در حالت اول بارگذاری و ضریب شدت تنش به صورت زیر است:

σ_ij: تنش‌های کوشی؛ x: فاصله نقطه مورد بررسی تا نوک ترک؛ θ: زاویه نقطه مورد بررسی نسبت به صفحه دربرگیرنده ترک؛ f_ij: توابع وابسته به هندسه ترک و شرایط بارگذاری

اروین کمیت K را «ضریب شدت تنش» (Stress Intensity Factor) نام‌گذاری کرد. از آنجایی که کمیت f_ij بدون بعد است، ضریب شدت تنش با واحد مگا پاسکال در جذر متر (MPam0.5) بیان می‌شود. با در نظر گرفتن مدل ریاضی «سخت‌کننده» (Stiffener) نیز یک عبارت مجانبی مشابه برای میدان تنش به دست می‌آید.

آزادسازی انرژی کرنشی

بر اساس مشاهدات اروین، در صورتی که اندازه ناحیه پلاستیک اطراف یک ترک نسبت به طول آن کوچک باشد، انرژی مورد نیاز برای رشد ترک وابستگی زیادی به حالت تنش در نوک ترک نخواهد داشت. به عبارت دیگر، در این حالت می‌توان از یک راه حل کاملاً الاستیک برای محاسبه مقدار انرژی قابل دسترس شکست استفاده کرد.

به این ترتیب، نرخ آزادسازی انرژی برای رشد ترک یا «نرخ آزادسازی انرژی کرنشی» (Strain Energy Release Rate) به صورت تغییرات انرژی کرنشی الاستیک بر واحد مساحت رشد ترک قابل محاسبه خواهد بود:

U: انرژی الاستیک سیستم؛ a: طول ترک؛ P: اندیس شرایط بارگذاری ثابت؛ u: اندیس شرایط جابجایی ثابت

اروین نشان داد که رابطه بین نرخ آزادسازی انرژی کرنشی و ضریب شدت تنش برای ترک حالت اول (بازشدگی) به صورت زیر بیان می‌شود:

E: مدول یانگ؛ v: نسبت پواسون؛ K_I: ضریب شدت تنش حالت اول

علاوه بر این، اروین نشان داد که نرخ آزادسازی انرژی کرنشیِ یک ترک مسطح در یک جسم الاستیک خطی برای اکثر شرایط بارگذاری عمومی را می‌توان با توجه به ضریب شدت تنش برای ترک‌های حالت اول، حالت دوم (لغزش) و حالت سوم (پارگی) بیان کرد.

در قدم بعدی، اروین فرض کرد که اندازه و شکل ناحیه اتلاف انرژی در طی شکست ترد تقریباً ثابت باقی می‌ماند. بر اساس این فرضیات، انرژی مورد نیاز برای ایجاد یک واحد سطح شکست، ثابتی است که تنها به نوع ماده بستگی دارد. این ثابت، یک ویژگی مادی جدید با عنوان «چقرمگی شکست» (Fracture Toughness) بود که با G_Ic نمایش داده می‌شد. امروزه، این ثابت با نام ضریب شدت تنش بحرانی (K_Ic) و به عنوان ویژگی معرف مکانیک شکست الاستیک خطی شناخته می‌شود (شرایط کرنش صفحه‌ای).

ناحیه پلاستیک نوک ترک

از نظر تئوری، در نقطه‌ای نزدیک به شعاع صفر، تنش موجود در نوک ترک بی‌نهایت خواهد بود. این مسئله را می‌توان به عنوان تکینگی تنش در نظر گرفت. باید توجه داشت که وجود تکینگی تنش در مسائل واقعی امکان‌پذیر نیست. به همین دلیل، در مطالعات عددی حوزه مکانیک شکست، استفاده از شکاف‌های مدور و نوک‌تیز برای نمایش ترک‌ها روش مناسب‌تری به شمار می‌رود که در آن به جای تکینگی نوک تر از یک ناحیه تمرکز تنش وابسته به هندسه استفاده می‌شود. بر اساس آزمایش‌های صورت گرفته، تمرکز تنش نوک ترک در مواد واقعی دارای یک مقدار محدود اما بزرگ‌تر از تنش اسمی اعمال شده بر روی نمونه است. مقدار تنش‌های موجود در نزدیکی نوک یک ترک را می‌توان با کمک معادله زیر محاسبه کرد:

σ_l: مقدار تنش در نزدیکی نوک ترک؛ σ: مقداری وابسته به تنش اسمی اعمال شده؛ Y: ضریب تصحیح وابسته به هندسه نمونه؛ r: فاصله شعاعی تا نوک ترک

 

به این ترتیب، حتماً یک ویژگی یا مکانیسم خاص درون ماده وجود دارد که مانع از گسترش خود به خودی ترک می‌شود. بر اساس فرضیات، تغییر شکل پلاستیک در نوک ترک، تیزی آن را کاهش می‌دهد. این تغییر شکل پیش از هر چیزی به تنش اعمال شده در راستای مناسب (در اکثر موارد، راستای y در دستگاه مختصات کارتزین)، طول ترک و هندسه نمونه بستگی دارد.

جورج اروین به منظور تخمین چگونگی گسترش ناحیه تغییر شکل پلاستیک، مقاومت تسلیم ماده را با تنش‌های میدان‌های دور در راستای y و در امتداد ترک (راستای x) برابر قرار دارد. سپس، معادله به دست آمده را نسبت به شعاع مؤثر حل کرد. اروین با استفاده از این رابطه، معادله زیر را برای تعیین شعاع ایدئال ناحیه پلاستیک در نوک ترک به دست آورد:

مدل‌های ارائه شده برای مواد ایدئال، قرارگیری ناحیه پلاستیک به دست آمده از رابطه بالا در مرکز نوک ترک را تأیید می‌کنند. رابطه بالا، شعاع ایدئال تغییر شکل ناحیه پلاستیک در بخش بالایی نوک ترک را به دست می‌آورد. این شعاع در بسیاری از علوم مرتبط با سازه کاربرد دارد؛ چراکه مقدار آن تقریب خوبی برای درک نحوه رفتار ماده در هنگام اعمال تنش است.

پارامترهای ضریب شدت تنش و شاخص چقرمگی ماده (K_C) و تنش تسلیم (σ_Y) اطلاعات زیادی را راجع به ماده، خواص آن و اندازه ناحیه پلاستیک نمایش می‌دهند. به همین دلیل، این پارامترها از اهمیت بالایی برخوردار هستند. به عنوان مثال، در صورت بالا بودن مقدار K_C، می‌توان نتیجه گرفت که ماده چقرمه (در برابر شکست مقاوم) است.

در طرف مقابل، اگر مقدار σ_Y زیاد باشد، می‌توان به شکل‌پذیری بیشتر ماده پی برد. نسبت این دو پارامتر نیز برای تعیین شعاع ناحیه پلاستیک اهمیت دارد. در صورتی که σ_Y کوچک باشد، نسبت مربع K_C به σ_Y (مانند رابطه بالا) بزرگ خواهد بود. در نتیجه، شعاع ناحیه پلاستیک نیز مقدار بزرگی خواهد شد. این وضعیت نشان می‌دهد که ماده می‌تواند به صورت پلاستیک تغییر شکل دهد و بنابراین چقرمه است. در مجموع، تخمین اندازه ناحیه پلاستیک در بالای نوک ترک را می‌توان به منظور تحلیل دقیق‌تر نحوه رفتار ماده در حضور ترک‌ها مورد استفاده قرار داد.

بارگذاری چرخه‌ای نیز فرآیندی مشابه با مراحل بالا را شامل می‌شود. اگر یک نمونه تحت بارگذاری چرخه‌ای دارای ترک باشد، تغییر شکل پلاستیک در محل نوک ترک رخ خواهد داد و رشد آن با تأخیر مواجه خواهد شد. در صورت وجود نوسان یا بارگذاری اضافی، مدل فعلی به میزان کمی تغییر می‌کند. دلیل این امر، مطابقت مدل با افزایش ناگهانی تنش نسبت به شرایط بارگذاری قبلی است.

در بارگذاری‌های بزرگ (بارگذاری اضافی)، رشد ترک تا بیرونِ ناحیه پلاستیک ادامه می‌یابد و از محدوده تغییر شکل پلاستیک اولیه عبور می‌کند. اگر فرض کنیم که بزرگی تنش اضافی برای ایجاد شکست کامل در نمونه کافی نباشد، ترک در محل نوک جدید خود تحت تأثیر تغییر شکل پلاستیک بیشتر قرار می‌گیرد. این مسئله باعث بزرگ‌تر شدن ناحیه تنش‌های پسماند پلاستیک می‌شود. فرآیند مذکور، چقرمگی و عمر ماده را افزایش می‌دهد؛ چراکه ناحیه پلاستیک جدید از ناحیه پلاستیک در شرایط اعمال تنش عادی بزرگ‌تر خواهد بود. علاوه بر این، افزایش ناحیه پلاستیک، ظرفیت ماده در برابر تحمل بارگذاری چرخه‌ای را نیز بهبود می‌بخشد.

چقرمگی شکست و روش‌های آزمایش آن

چقرمگی خاصیتی است که میزان مقاومت یک ماده در برابر شکست را بیان می‌کند. این خاصیت مکانیکی، از اهمیت بالایی در مسائل مهندسی برخوردار است. چندین روش مختلف آزمایش برای اندازه‌گیری چقرمگی شکست ماده وجود دارد. در این آزمایش‌ها معمولاً از یک نمونه شیاردار در یکی از چندین پیکربندی موجود استفاده می‌شود. با توجه به اهداف مقاله پیش رو، در این بخش به معرفی روش‌های تعیین چقرمگی شکست کرنش صفحه‌ای (K_Ic) خواهیم پرداخت.

هنگامی که یک ماده پیش از شکست، رفتار الاستیک خطی از خود به نمایش می‌گذارد (مانند حالتی که ناحیه پلاستیک در مقایسه با ابعاد نمونه کوچک است)، مقدار بحرانی ضریب شدت تنش برای ترک حالت اول را می‌توان به عنوان یک پارامتر شکست مناسب در نظر گرفت. این روش با توجه به ضریب شدت تنش بحرانی برای کرنش صفحه‌ای، یک معیار کمی از چقرمگی شکست را ارائه می‌کند. به منظور اطمینان از معنادار بودن نتایج باید پس از اتمام هر آزمایش، اعتبارسنجی‌های مورد نیاز صورت گیرد. ابعاد نمونه باید ثابت و به اندازه‌ای بزرگ باشند که شرایط کرنش صفحه‌ای در نوک ترک را تضمین کنند. این الزامات باعث محدودیت در نحوه اجرای آزمایش می‌شوند.

نکته اصلی در آزمایش‌های مبتنی بر چقرمگی شکست (K) این است که باید از قرار داشتن شکست‌های نمونه تحت شرایط الاستیک خطی اسمی اطمینان حاصل کرد. این مسئله لزوم کوچک بودن ناحیه پلاستیک در مقایسه با مقطع نمونه را نشان می‌دهد.

آزمایش چقرمگی شکست در شرایط کرنش صفحه‌ای

نمونه‌های خمش شکاف تک لبه‌ای (SENB یا خمش سه‌نقطه‌ای) و نمونه‌های فشرده کششی (C_T)، متداول‌ترین پیکربندی‌های آزمایش چقرمگی شکست هستند. برای تعیین دقیق چقرمگی شکست کرنش صفحه‌ای باید نمونه‌ای را انتخاب کرد که ضخامت آن از یک مقدار بحرانی (B) بیشتر باشد. بر اساس آزمایش‌های صورت گرفته، شرایط کرنش صفحه‌ای در صورت صادق بودن رابطه زیر کاربرد دارد:

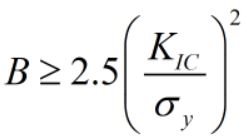
B: حداقل ضخامتی که باعث ایجاد کمترین انرژی کرنش پلاستیک در نوک ترک می‌شود؛ K_IC: چقرمگی شکست ماده؛ s_y: تنش تسلیم ماده

هنگامی که یک ماده با چقرمگی شکست مجهول مورد آزمایش قرار می‌گیرد، از نمونه‌ای با ضخامت مقطع کامل یا اندازه‌ای متناسب با چقرمگی پیش‌بینی شده آن استفاده می‌شود. اگر مقدار چقرمگی شکست حاصل از آزمایش در رابطه بالا صدق نکند، باید آزمایش را با یک نمونه ضخیم‌تر تکرار کرد. هنگامی که یک آزمایش قادر به برطرف کردن الزامات مورد نیاز (مانند ضخامت) به منظور اطمینان از وجود شرایط کرنش صفحه‌ای نباشد، مقادیر به دست آمده چقرمگی شکست با K_C نمایش داده خواهند شد.

حالت‌های تنش صفحه‌ای و تنش انتقالی

در مواقعی که انرژی پلاستیک نوک ترک قابل اغماض نیست، پارامترهای دیگر مکانیک شکست (مانند انتگرال J و منحنی R) برای تعیین خصوصیات ماده مورد استفاده قرار می‌گیرند. داده‌های به دست آمده از آزمایش‌های دیگر به ضخامت نمونه مورد آزمایش بستگی خواهند داشت و به عنوان خواص واقعی ماده محسوب نخواهند شد. اگرچه، شرایط کرنش صفحه‌ای در تمام پیکربندی‌های سازه صادق نیست. از این‌رو، استفاده از مقادیر K_IC در طراحی نواحی نسبتاً نازک می‌تواند منجر به نتایج بسیار محافظه‌کارانه و در نتیجه افزایش وزن و هزینه ساخت آن شود.

در مواردی که حالت تنش واقعی به صورت صفحه‌ای یا انتقالی باشد، به کارگیری داده‌های به دست آمده از انتگرال J و نمودار R مناسب‌تر خواهد بود. این حالت برای شکست‌های آرام و پایدار (پارگی شکل‌پذیر) نسبت به شکست‌های سریع (شکننده) کاربرد بیشتری دارد. شرط در نظر گرفتن حالت تنش صفحه‌ای یا انتقالی به صورت زیر است:

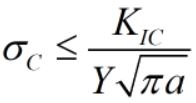
σ_c: تنش بحرانی اعمال شده که باعث ایجاد شکست می‌شود؛ K_IC: چقرمگی شکست کرنش صفحه‌ای؛ Y: یک ثابت عددی مرتبط با هندسه نمونه؛ a: طول ترک برای ترک‌های لبه‌ای یا نصف طول ترک برای ترک‌های داخلی

محدودیت‌های مکانیک شکست الاستیک خطی

یکی از مشکلاتی که محققان آزمایشگاه تحقیقاتی وابسته به نیروی دریایی ایالات متحده با آن مواجه شدند، رفتار مواد مورد استفاده در ساخت کشتی‌ها (نظیر ورق‌های فولادی بدنه کشتی) بود. این مواد رفتار کاملاً الاستیک ندارند و نوک ترک‌های موجود بر روی آن‌ها نیز در معرض مقدار قابل توجهی از تغییر شکل‌های پلاستیک قرار می‌گیرد. کوچک بودن مقیاس تسلیم ماده به عنوان یکی از فرضیات اساسی اروین در مکانیک شکست در نظر گرفته می‌شود (کوچک بودن اندازه ناحیه پلاستیک نسبت به طول ترک).

با این وجود، این فرضیه برای انواع بخصوصی از شکست در فولادهای ساختمانی دارای محدودیت است و امکان ایجاد شکست‌های ترد در این مواد فولادی و رخ دادن حوادث فاجعه‌بار وجود دارد. در مجموع، کاربرد مکانیک شکست الاستیک خطی برای فولادهای ساختمانی محدود بوده و استفاده از آزمایش‌های چقرمگی شکست نیز هزینه‌بر است. به همین دلیل، در این شرایط باید از رویکردهای مکانیک شکست الاستیک-پلاستیک استفاده کرد.

ملاحظات مکانیک شکست در کاربردهای مهندسی

به منظور اجرای تحلیل و پیش‌بینی گسیختگی در مکانیک شکست به اطلاعات زیر نیاز است:

• بار اعمال شده
• تنش پسماند
• شکل و اندازه قطعه مورد آزمایش
• شکل، اندازه، محل قرارگیری و جهت‌گیری ترک

تمامی اطلاعات بالا همیشه در دسترس نخواهند بود. به همین دلیل، معمولاً از فرضیات محافظه‌کارانه برای انجام تحلیل‌ها کمک گرفته می‌شود. گاهی اوقات نیز تحلیل‌های مکانیک شکست پس از رخ دادن گسیختگی مورد استفاده قرار می‌گیرند. اگر شکست در عدم حضور بارهای اضافی رخ داده باشد، وجود ترک‌های بسیار بزرگ شناسایی نشده در حین بررسی‌های معمول یا چقرمگی پایین ماده به عنوان دلایل رخ دادن شکست در نظر گرفته می‌شوند.

روابط ریاضی مکانیک شکست

در بخش انتهایی، به معرفی متداول‌ترین روابط ریاضی موجود در مکانیک شکست می‌پردازیم.

معیار گریفیث

برای مسائل ساده‌ای نظیر ورق‌های نازک مستطیلی به همراه یک ترک عمود بر راستای بارگذاری، تئوری گریفیث به فرم زیر درمی‌آید:

G: نرخ آزادسازی انرژی کرنشی؛ σ: تنش اعمال شده؛ a: نصف طول ترک؛ E: مدول یانگ که در شرایط کرنش صفحه‌ای باید بر ضریب سختی ورق (1-v²) تقسیم شود.

در یک تعریف دیگر، نرخ آزادسازی انرژی کرنشی به صورت نرخ جذب انرژی توسط رشد ترک در نظر گرفته می‌شود. با جایگذاری تنش در لحظه شکست (σ_f) به جای تنش اعمال شده خواهیم داشت:

شرط G≥G_c به عنوان معیاری برای شروع رشد ترک در نظر گرفته می‌شود.

اصلاحات اروین

سرانجام با ارائه یک فرم اصلاح شده برای معیار گریفیث، شدت تنش جایگزین نرخ آزادسازی انرژی کرنشی و چقرمگی شکست جایگزین انرژی نقطه ضعف سطحی شد. رابطه بین این پارامترهای جدید و پارامترهای معرفی شده توسط گریفیث به صورت زیر نوشته می‌شود:

برای تنش صفحه‌ای داریم:

و برای کرنش صفحه‌ای داریم:

K_I: شدت تنش؛ K_c: چقرمگی شکست؛ v: نسبت پواسون

توجه به این ضروری است که مقادیر اندازه‌گیری پارامتر شکست (K_c) در شرایط کرنش صفحه‌ای و تنش صفحه‌ای با هم متفاوت هستند. شکست زمانی رخ می‌دهد که شرط K_I≥K_c برقرار باشد. برای موارد خاص تغییر شکل در شرایط کرنش صفحه‌ای، K_c به K_Ic تبدیل شده و به عنوان یکی از خواص ماده در نظر گرفته می‌شود. اضافه شدن اندیس I در این پارامتر، به دلیل روش‌های مختلف بارگذاری برای ایجاد رشد ترک در ماده است. در واقع این اندیس، حالت اول (Mode I) بارگذاری را نمایش می‌دهد.

رابطه‌ای که در بالا برای K_I ارائه شد، تنها در ورق بی‌نهایت به همراه ترک مرکزی قابل استفاده است. این رابطه برای هندسه‌های دیگر تغییر می‌کند. به همین دلیل، به منظور تعیین هندسه باید از یک ضریب تصحیح بی‌بعد (Y) استفاده کرد. به این ترتیب داریم:

Y، تابعی از طول ترک و عرض ورق است که برای ورقی با عرض محدود W که ترکی با طول 2a در راستای ضخامت آن قرار گرفته، داریم:

و ورقی با عرض محدود W که یک ترک لبه‌ای با طول a در راستای ضخامت آن قرار گرفته، داریم:

الاستیسیته و پلاستیسیته

از آنجایی که مهندسان به استفاده از پارامتر K_Ic برای تعیین چقرمگی شکست عادت کرده‌اند، رابطه زیر برای تبدیل J_Ic به این پارامتر ارائه شده است:

برای تنش صفحه‌ای داریم:

و برای کرنش صفحه‌ای داریم:

^^