پایداری با دقت مرتبه اول — به زبان ساده

در مطالب گذشته وبلاگ فرادرس در مورد مفاهیم پایداری و همچنین تابعی تحت عنوان تابع لیاپانوف صحبت کردیم. این تابع به ما کمک می‌کرد تا بتوانیم وضعیت پایداری یک سیستم را بررسی کنیم. در این مطلب قصد داریم تا در مورد پایداری با دقت مرتبه اول صحبت کنیم.

پایداری با دقت مرتبه اول

به منظور بررسی پایداری، در ابتدا سیستمی خودکار از $$n$$ معادله دیفرانسیل را به صورت زیر در نظر بگیرید.

$$\large { \frac { {d { x_ i } } } { { d t } } = { f _ i } \left( { { x _ 1 } ,{ x _ 2 } , \ldots ,{ x _ n } } \right ),\;\; } \kern0pt { i = 1,2, \ldots ,n }$$

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

سیستم معادلات فوق را می‌توان به صورت برداری، مطابق با عبارت زیر نیز بیان کرد.

$$ \large { \mathbf { X ^ { \prime } } = \mathbf { f } \left ( \mathbf{X} \right),\;\;} \kern0pt {\text{where}\;\;\mathbf { X } = \left[ {\begin{array}{*{20} { c } } { { x _ 1 } } \\ {{x_2}}\\ \vdots \\ {{x_n}} \end{array}} \right],\;\;}\kern0pt {\mathbf{f} = \left[ {\begin{array}{*{20 } { c } } { { f _ 1} } \\ { { f _ 2 } } \\ \vdots \\ { { f _ n } } \end{array}} \right] } $$

فرض کنید $$\mathbf { X } = \mathbf { 0 }$$ نقطه تعادل سیستم باشد که هدف نیز بررسی پایداری آن است. هم‌چنین فرض بر این است که $${ f _ i } \left ( \mathbf { X } \right )$$ در نزدیکی مبدا دوبار مشتق‌پذیر بوده و این مشتق نیز پیوسته باشد. از این رو می‌توانیم توابع $$x_i$$ را به صورت زیر و در قالب بسط مک‌ لورن بیان کنیم. البته مشتقات مرتبه دوم و بالاتر در نظر گرفته نمی‌شوند. به همین دلیل به این روش، پایداری با دقت مرتبه اول گفته می‌شود.

$$\large \begin {gather*} {\frac { { d{ x _ i } } } { { d t } } = \frac { { \partial { f _ i} } } { { \partial { x _1 } } } \left( 0 \right) { x_1} + \frac { { \partial { f _ i} } } { { \partial { x _2 } }} \left( 0 \right ) { x _ 2 } + \cdots } \\\\ + { \frac { { \partial {f _ i} } } { { \partial {x _ n} } }\left( 0 \right ) { x _n } } + { { R _ i } \left( {{x_1},{x_2}, \ldots ,{x_n } } \right) } \end {gather*}$$

در این‌جا $${ R _ i } \left ( { { x _ 1 } , { x _2 } , \ldots ,{ x _ n } } \right )$$ نشان‌دهنده ترم‌های مرتبه دوم نسبت به متغیر‌های $${ { x _ 1 } , { x _ 2 } , \ldots { x _ n } }$$ است. بسط مک‌لورن ارائه شده در بالا را می‌توان به صورت برداری-ماتریسی، همان‌طور که در ادامه آمده، بیان کرد:

$$\mathbf { X ^ { \prime } } = J \mathbf { X } + \mathbf { R } \left ( \mathbf { X } \right )$$

ژاکوبینِ $$J$$ را می‌توان مطابق با رابطه زیر بیان کرد:

$$ \large J = \left[ {\begin{array}{*{20}{c}}<br /> { \frac { { \partial { f _ 1 } } } { { \partial { x _ 1 } } } } & { \frac { { \partial { f _ 1 } } } { { \partial { x _ 2 } } } } & \vdots &{\frac{{\partial { f _1 } }} { {\partial { x _ n } } } } \\ { \frac { { \partial { f _ 2 } } } { { \partial { x _ 1 } } } } & { \frac { { \partial {f_2 } } } { {\partial { x _ 2 } } } } & \vdots &{\frac { { \partial { f _ 2 } } } { { \partial { x _ n } } } } \\ \cdots & \cdots & \vdots & \cdots \\ {\frac{{\partial { f _ n } } } { { \partial { x _ 1} } } } & { \frac{{\partial { f _ n } } } { { \partial { x _ 2 } } } } & \vdots & { \frac { { \partial { f _ n } } } { { \partial { x _ n } } } }<br /> \end{array} } \right] $$

توجه داشته باشید که مقادیر مشتقات جزئی تشکیل‌دهنده ماتریس فوق،‌ در نقطه بسط داده شده، یعنی $$X=0$$ محاسبه می‌شوند. در مطالعه پایداری، سیستم‌های خطی را می‌توان مطابق با رابطه زیر در نظر گرفت.

$$\large \mathbf { X ^ { \prime } } = J \mathbf { X }$$

بر خلاف معادله غیر خطی بیان شده، از معادله فوق در این مطلب استفاده می‌کنیم. این معادله خطی بوده و از مرتبه اول است. پایداری سیستمی که در آن مشخصه‌های سیستمِ غیرخطیِ اصلی و سیستم مرتبه اولِ مرتبط با آن مشابه باشند، توسط لیاپانوف توضیح داده شده است. در ادامه برخی از نتایج نظریه لیاپانوف ارائه شده‌اند.

نظریه لیاپانوف در پایداری و ناپایداری مرتبه اول

اگر حداقل یکی از مقادیر ویژه $${ \lambda _ i }$$ مربوط به ماتریس ژاکوبین ($$J$$) دارای مقداری مثبت در بخش حقیقی خود باشد، در این صورت پاسخ صفرِ $$X=0$$ معادله سیستم خطی شده، ناپایدار است. به همین صورت می‌توان گفت اگر تمامی مقادیر ویژه $${ \lambda _ i }$$ دارای بخش حقیقی منفی باشند، در این صورت پاسخ صفرِ $$X=0$$ پایدار است.

فیلم آموزش سیستم های کنترل غیر خطی با رویکرد حل مساله در فرادرس

کلیک کنید

در موارد بحرانی که تمامی مقادیر ویژه ماتریس ژاکوبین منفی و صفر هستند، وضعیت پایداری مبهم بوده و ریشه‌های صفر ممکن است وضعیتی پایدار یا ناپایدار داشته باشند. در این موارد نمی‌توان از روش پایداری مرتبه اول استفاده کرده و باید از روش‌های دیگری به منظور بررسی پایداری استفاده کرد. بنابراین از روش لیاپانوف زمانی می‌توان استفاده کرد که بخش حقیقی مقادیر ویژه ماتریس ژاکوبین غیر صفر باشند.

موقعیت تعادل ریشه $$\mathbf { X } = \mathbf { 0 }$$ سیستمی از مرتبه $$n$$ را در نظر بگیرید. این سیستم در زیر ارائه شده است.

$$\large \mathbf { X ’ } = \mathbf { f } \left ( \mathbf { X } \right )$$

به چنین سیستمی در صورتی که بخش حقیقی مقادیر ویژه ماتریس ضرایب آن غیر صفر باشد، «ناهموار» (Rough) گفته می‌شود. در این حالت ماتریس $$J$$ دقیقا $$n$$ مقدار حقیقی مجزا دارد.

توجه داشته باشید در مواردی که با سیستمی از مرتبه دو روبرو هستیم، فقط یکی از سه حالت زیر، ناهموار محسوب می‌شوند.

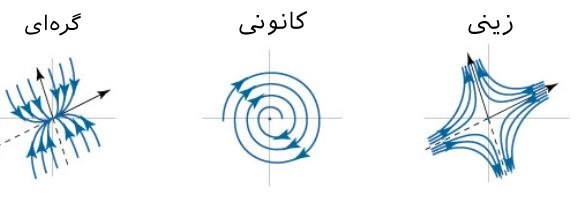
نهایتا می‌توان گفت که روش پایداری مرتبه اول را می‌توان تنها برای بررسی پایداری سیستم‌های ناهموار (سیستم‌هایی با پایداری ساختاری) استفاده کرد. در ادامه مثال‌هایی ذکر شده که پیشنهاد می‌شود آن‌ها را مطالعه فرمایید.

مثال ۱

پایداری نقطه تعادلِ سیستمِ زیر را با استفاده از تقریب مرتبه اول بررسی کنید.

$$\large { \frac { { d x } } { { d t } } = y + 3 { x ^2 } + 2 { y^ 2 } \;,\;\;} \kern0pt { \frac { { d y } } { { d t } } = – 2 x – y + x y }$$

در این مسئله توابع $$f _ 1$$ و $$f _ 2$$ به صورت زیر هستند.

$$\large { { { f_ 1 } \left ( { x ,y } \right) } = { y + 3 { x ^ 2 } + 2 { y ^ 2 } \;\;} } \kern-0.3pt { { { f _ 2 } \left( { x , y } \right ) } = { – 2x – y + xy } }$$

بدیهی است که این توابع پیوسته بوده و در همسایگی نقطه تعادلِ $$X=0$$ نیز مشتق‌پذیر هستند. هم‌چنین واضح است که بزرگی ترم‌های غیرخطی از مرتبه ۲ است. از این رو این سیستم تمامی ملزومات لازم به منظور بررسی با تقریب مرتبه اول را دارا خواهد بود. در اولین قدم باید اجزا ماتریس ژاکوبین را در نقطه $$X=0$$ به صورت زیر بدست آورد.

$$\large \begin {align*} { \frac { { \partial { f _ 1 } } } { { \partial x } } = 6 x , \;\;} \kern-0.3pt { \frac{{\partial { f _ 1} } } { { \partial y } } = 1 + 6y,\;\;}\kern-0.3pt { \frac { { \partial { f_ 2 } } } { { \partial x } } = – 2 + y,\;\;}\kern-0.3pt { \frac { { \partial { f _ 2 } } } { { \partial y } } = – 1 + x } \end {align*}$$

$$ \large \begin {gather*} \require{AMSmath.js} \Rightarrow{ {\left. {\frac{{\partial { f _1 } } } { { \partial x} } } \right|_{\substack{ x = 0 \\ y = 0 } } } = 0,\;\;} \kern-0.3pt {{\left. {\frac{{\partial { f _ 1} } } { { \partial y} } } \right|_{\substack{ x = 0\\ y = 0 } } } = 1,\;\;}\kern-0.3pt { { \left. {\frac{{\partial { f _ 2} } } { { \partial x } } } \right|_{\substack{ x = 0\\ y = 0} } } = – 2 \;\;} \\\\ \kern-0.3pt { { \left. {\frac { { \partial { f _ 2 } }} {{ \partial y } } } \right|_{\substack{ x = 0\\ y = 0} } } = – 1,\;\;}\kern-0.3pt { \Rightarrow J = \left[ {\begin{array}{*{20}{r}} 0&1\\ { – 2}&{ – 1} \end{array}} \right] } \end {gather*} $$

بنابراین مقادیر ویژه برابرند با:

$$ \large \begin {align*} {\det \left ( { J – \lambda I} \right) = 0 \;\;} & \Rightarrow {\left| {\begin {array}{*{20} { c } } {0 – \lambda } & 1 \\<br /> { – 2}&{ – 1 – \lambda } \end {array}} \right| = 0 \;\;} \\ & \Rightarrow { \lambda \left( { \lambda + 1} \right) + 2 = 0 \;\;} \\ & \Rightarrow { { \lambda ^ 2 } + \lambda + 2 = 0 \;\;} \\ & \Rightarrow {D = – 7 \;\;} \\ & \Rightarrow { { \lambda _{1,2}} = \frac{{ – 1 \pm \sqrt { – 7} } } { 2 } } = { – \frac { 1 } { 2 } \pm \frac{{i\sqrt 7 } } { 2 } } \end {align*} $$

معادله مشخصه دو ریشه مختلط دارد که بخش حقیقی آن‌ها منفی هستند.

$$\large { \text {Re} \left[ { { \lambda _ 1 } } \right] \lt 0,\;\;} \kern-0.3pt { \text {Re} \left[ { { \lambda _ 2 } } \right] \lt 0 }$$

بنابراین می‌توان گفت که پاسخ صفر سیستم از نظر تئوری پایداری مرتبه اول، پایدار است. توجه داشته باشید که نقطه تعادل این سیستم از نوع کانونی است.

مثال ۲

نقطه تعادل سیستم زیر را یافته و پایداری آن را با استفاده از تقریب مرتبه اول بیابید.

$$\frac { { d x } } { { d t } } = { x ^ 2 } – y \; ,\;\; \frac { { d y } } { { d t } } = x – 1$$

فیلم آموزش طراحی سیستم های کنترل غیر خطی در فرادرس

کلیک کنید

در ابتدا نقطه تعادل را با استفاده از صفر قرار دادن معادلات به صورت زیر بدست می‌آوریم.

$$ \large {\left\{ \begin{array}{l}<br /> \frac { { d x } } { { d t } } = 0 \\ \frac { { d y } } { { d t } } = 0 \end{array} \right. \;\;} \Rightarrow {\left\{ {\begin {array}{*{20}{ l } } { { x ^ 2 } – y = 0} \\ {x – 1 = 0} \end{array}} \right. \;\;} \Rightarrow<br /> {\left\{ {\begin{array}{*{20}{l}} {x = 1} \\ {y = 1} \end {array}} \right. } $$

با توجه به این که نقطه $$(1, 1 )$$، پاسخ صفر محسوب نمی‌شود، از تغییر متغیر زیر استفاده می‌کنیم.

$$\large { u = x – 1 \; , \;\;} \kern-0.3pt { v = y – 1 }$$

با قرار دادن تغییر متغیر فوق در معادله اصلی داریم:

$$ \large \begin {gather*} \require{cancel} {\left\{ \begin{array}{l} {\frac { { d \left ( { u + 1 } \right) } } {{ d t } } }={ {\left( {u + 1} \right)^2} } - { \left( {v + 1} \right) } \\ { \frac { { d \left( {v + 1} \right ) } } { { d t } } } = { u + \cancel {1} }-{ \cancel{1} } \end {array} \right. \;\;} \\ \\ \Rightarrow {\left\{ {\begin{array}{*{20}{ l } } {{\frac{ { d u } } { {d t }} } = { { u ^ 2 } + 2u }+{ \cancel{1} – v – \cancel { 1 } } } \\ { \frac { { d v } } { { d t } } = u} \end{array}} \right. \;\;} \Rightarrow { \left\{ {\begin {array}{*{20} { l } } { \frac { { d u} } {{ d t} } = { u ^ 2 } + 2u – v } \\ { \frac {{ d v } } { {d t } } = u } \end{array}} \right.} \end {gather*} $$

به منظور تعیین کردن پایداری پاسخ صفر، ژاکوبینِ $$J$$ باید محاسبه شود. در نتیجه در ابتدا توابع $$f$$ را به‌صورت زیر در نظر می‌گیریم:

$$\large { { { f _ 1 } \left ( { u , v } \right ) } = { { u ^ 2 } + 2 u – v,\;\;} } \kern-0.3pt { { f _2 } \left ( { u , v } \right ) = u }$$

بنابراین مشتقات جزئی برابرند با:

$$\large {{\frac { { \partial { f _1 } } } { { \partial u}} = 2u + 2 \; ,\;\;} \kern-0.3pt { \frac { { \partial { f _1 } }} { { \partial v}} = – 1 \; ,\;\;} \kern-0.3pt { \frac { { \partial { f _ 2} } } { { \partial u } } = 1 \; ,\;\;}\kern-0.3pt { \frac { { \partial { f _2 } } } { { \partial v } } = 0 } }$$

به همین صورت مشتق جزئی در نقطه $$(u = 0 ,v = 0)$$ نیز برابر است با:

$$\large { { \left. {\frac{{\partial { f _ 1} } } { {\partial u } } } \right|_{\substack { u = 0 \\ v = 0 } } } = 2,\;\;}\kern-0.3pt {{\left. {\frac{{\partial { f_ 1 } } } { { \partial v } } } \right|_{\substack { u = 0 \\ v = 0 } } } = – 1,\;\;} \kern-0.3pt {{\left. {\frac{{\partial { f _2 } } }{ {\partial u } } } \right|_{\substack{ u = 0 \\ v = 0 } } } = 1,\;\;}\kern-0.3pt {{\left. {\frac{{\partial { f _2 } } } { { \partial v } } } \right|_{\substack { u = 0 \\ v = 0 } } } = 0 }$$

هم‌چنین مقادیر ویژه ماتریس $$J$$ برابر است با:

$$ \large \begin {gather*} {J = \left[ {\begin{array}{*{20}{r}} 2 & { – 1} \\ 1 & 0 \end{array}} \right],\;\;}\kern-0.3pt {\det \left( {J – \lambda I} \right) = 0,\;\;} \Rightarrow {\left| {\begin{array}{*{20}{c}} {2 – \lambda } & { – 1}\\ 1&{0 – \lambda } \end{array}} \right| = 0,\;\;} \\ \\ \Rightarrow { \lambda \left( {\lambda – 2} \right) + 1 = 0,\;\;} \Rightarrow { { \lambda ^ 2 } – 2\lambda + 1 = 0,\;\;} \\ \\ \Rightarrow { { \left( {\lambda – 1} \right)^2} = 0,\;\;} \\ \\ \Rightarrow { { \lambda _ {1 , 2 } } = 1.} \end {gather*} $$

بنابراین ماتریس $$J$$ دارای مقدار ویژه‌ای تکراری برابر با $$\lambda = 1$$ است. با توجه به تعریف یک نقطه پایدار با استفاده از مقادیر ویژه متفاوت توصیف می‌شود. با توجه به یکسان بودن این مقادیر برای این سیستم، نمی‌توان این سیستم را با استفاده از پایداری مرتبه اول بررسی کرد. برای تحلیل درست می‌توان از روش‌های دیگری همچون تابع لیاپانوف استفاده کرد.

مثال ۳

موقعیت‌های پایدار سیستم زیر را یافته و پایداری آن را بررسی کنید. هم‌چنین شماتیکی از فاز‌های سیستم خطی مرتبط با آن را ترسیم کنید.

$$\large { \frac { { d x } } { { d t } } = { e ^ { x + y } } – 1,\;\;} \kern0pt{\frac { { d y } } { { d t } } = \ln \left( { 1 + x } \right ) }$$

فیلم مجموعه آموزش مهندسی کنترل – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

در ابتدا نقاط پایدار سیستم را با حل سیستم جبری زیر بدست می‌آوریم.

$$\large {\left\{ \begin{array} { l } \frac { { d x } } { { d t } } = 0 \\ \frac { { d y } } { { d t } } = 0 \end{array} \right. \;\;}\Rightarrow {\left\{ \begin {array} { l } { e ^ { x + y } } – 1 = 0 \\ \ln \left ( { 1 + x } \right ) = 0 \end {array} \right. }$$

معادله دوم، مقدار $$x = 0$$ را نتیجه می‌دهد. با قرار دادن آن در معادله اول مقدار $$y$$ برابر با عدد زیر بدست می‌آید.

$$\large { { e ^ y } – 1 = 0 , \;\; } \Rightarrow { { e ^ y } = 1 \;\; } \Rightarrow { y = 0 }$$

بنابراین سیستم دارای تنها یک نقطه تعادل است ($$x= \ 0,y= \ 0$$). به منظور بررسی پایداری پاسخ صفر، سمت راست دستگاه معادله دیفرانسیل را در قالب بسط مک‌ لورن می‌نویسیم.

$$\large { { f _ 1 } \left( { x , y } \right ) = { e ^ {x + y } } – 1,\;\;} \kern-0.3pt { { f _ 2 } \left ( { x , y } \right ) = \ln \left ( {1 + x} \right) }$$

$$\large { \frac { { \partial { f _ 1 } } } { { \partial x } } = { e ^ { x + y } },\;\;} \kern-0.3pt { \frac { { \partial { f _ 1 } } } { { \partial y } } = { e ^ { x + y } } \;\;}\kern-0.3pt { \frac { { \partial { f _ 2 } } } { { \partial x } } = \frac{ 1 } { { 1 + x } } \;\;} \kern-0.3pt { \frac { { \partial { f _ 2 } } }{ { \partial y } } = 0 }$$

در ادامه مقادیر مشتقات جزئی در نقطه $$x = 0 \ , \ y = 0$$ برابر با مقادیر زیر بدست می‌آیند.

$$\large \begin {gather*} {{\left. {\frac{{\partial {f_1}}}{{\partial x}}} \right|_{\substack{ x = 0 \\ y = 0 } } } = 1,\;\;}\kern-0.3pt {{\left. {\frac{{\partial { f _1 }} } { { \partial y } } } \right|_{\substack{ x = 0\\ y = 0}}} = 1,\;\;} \\ \\ \kern-0.3pt {{\left. {\frac { { \partial { f _2 } } } { { \partial x}}} \right|_{\substack{ x = 0\\ y = 0}}} = 1,\;\;}\kern-0.3pt {{\left. {\frac{{\partial { f _ 2 } }} { {\partial y}}} \right|_{\substack{ x = 0\\ y = 0}}} = 0.} \end {gather*}$$

بنابراین مقادیر ویژه ماتریس ژاکوبین برابرند با:

$$ \large \begin {align*} { J = \left[ {\begin{array}{*{20} { c } }<br /> 1&1\\1&0 \end {array}} \right],\;\;} & \kern-0.3pt { \det \left( {J – \lambda I} \right ) = 0,\;\;} \\\\ & \Rightarrow {\left| {\begin {array}{*{20} { c } } {1 – \lambda } & 1 \\ 1&{0 – \lambda } \end {array}} \right| = 0,\;\; } \\\\ & \Rightarrow {\lambda \left ( { \lambda – 1} \right) – 1 = 0,\;\;} \\\\ & \Rightarrow { { \lambda ^ 2 } – \lambda – 1 = 0,\;\;} \\\\ & \Rightarrow { D = 5,\;\; } \\\\ & \Rightarrow { { \lambda _ { 1 , 2 } } = \frac { { 1 \pm \sqrt 5 } } { 2 } } = { \frac { 1 } { 2 } \pm \frac { { \sqrt 5 } } { 2 } } \end {align*} $$

همان‌طور که می‌بینید، مقادیر ویژه اعدادی حقیقی با علامت‌های متفاوت هستند.

$$\large { { { \lambda _1} = \frac { 1 } { 2 } + \frac { { \sqrt 5 }}{2} }\approx { 0.5 + 1.12 }={ 1.62,\;\;\;} } \kern-0.3pt { { { \lambda _2} = \frac{ 1 } { 2 } – \frac { { \sqrt 5 } } { 2 } }\approx { 0.5 – 1.12 }={ – 0.62} }$$

مقادیر ویژه نشان می‌دهند که سیستم خطی شده دارای تعادل صفر از نوع زینی است. نتیجه‌گیری مشابهی را می‌توان نسبت به سیستم غیرخطی اصلی داشت. در مرحله بعد باید بردار‌های ویژه را بدست آورد. معادله مربوط به مولفه‌های بردار ویژه اول به صورت زیر بدست می‌آیند.

$$ \large \begin {align*} \left ( { J – { \lambda _ 1 } I } \right ) & { \mathbf { V } _ 1 } = \mathbf { 0 } \;\; \\ \\ & \Rightarrow { { \left[ {\begin{array}{*{20}{ c } } { \frac { 1 } { 2 } – \frac{{\sqrt 5 }}{2}}&1\\ 1&{ – \frac{1}{2} – \frac{{\sqrt 5 } } { 2 } } \end{array}} \right] \cdot}\kern0pt{ \left[ {\begin{array}{*{20} { c } } { { V _{ 11 } } } \\ { { V _ { 21 } } } \end{array}} \right] = \mathbf{0},\;\;}} \\\\ & \Rightarrow {\left\{ {\begin{array}{*{20}{l}} {\left( {\frac{1}{2} – \frac{{\sqrt 5 } } { 2 } } \right){V_{11}} + {V_{21}} = 0 } \\ {{V_{11}} – \left( {\frac { 1 } { 2 } + \frac{{\sqrt 5 }}{2}} \right){V _ { 21 } } = 0} \end{array}} \right.,\;\;} \\\\ & \Rightarrow {\left\{ {\begin{array}{*{20} { l } } {\left( {\frac{1}{2} – \frac { { \sqrt 5 } } { 2 } } \right){V _ { 11 } } + { V _ { 21} } = 0 } \\ {\left( {\frac { 1 } { 2 } – \frac{{\sqrt 5 } } { 2 } } \right){V _ { 11 } } + {V_{21}} = 0} \end{array}} \right.,\;\;} \\\\ & \Rightarrow {\left( {\frac{1}{2} – \frac{{\sqrt 5 }}{2}} \right){V_{11}} + {V_{21}} = 0 } \end {align*} $$

به‌منظور حل دستگاه فوق در اولین قدم، مولفه $${ V _ { 11 } } = t$$ را در نظر می‌گیریم. با این فرض دیگر مولفه‌های بردار $$V _ 1$$ برابرند با:

$$ \large \begin {gather*} { { V _ { 21 } } = – \left( {\frac{1}{2} – \frac{{\sqrt 5 }}{2}} \right ) { V _ { 11 } } } = {- \left( {\frac{1}{2} – \frac{{\sqrt 5 }}{2}} \right)t \approx 0.62t,\;\;} \\ \\ \Rightarrow {{{\mathbf{V}_1} = \left[ {\begin{array}{*{20} { c } } { { V _ { 11 } } } \\ {{V_{21}}} \end{array}} \right] } = {\left[ {\begin{array}{*{20}{ c } } t \\ { 0.62 t } \end{array}} \right] } = { t \left[ {\begin{array}{*{20}{ c } } 1\\ { 0.62 } \end{array}} \right] } } \sim { { \left[ {\begin{array}{*{20} { c } } 1 \\ { 0.62 } \end {array}} \right] } } \end {gather*} $$

به طور مشابه بردار $$V_2$$ نیز به صورت زیر بدست خواهد آمد.

$$ \large \begin {gather*} \left ( { J – { \lambda _2}I} \right){\mathbf{V}_2 = \mathbf { 0 } ,\;\;} \Rightarrow {{\left[ {\begin{array}{*{20}{c}} {\frac{1}{2} + \frac{{\sqrt 5 }}{2}}&1\\ 1&{ – \left( {\frac{1}{2} – \frac{{\sqrt 5 }}{2}} \right)} \end{array}} \right] \cdot}}\kern0pt{{ \left[ {\begin{array}{*{20}{c}} {{V_{12}}}\\ { { V _ { 22 } } } \end{array}} \right] = \mathbf{0},\;\;} } \\ \\ \Rightarrow {\left\{ {\begin{array}{*{20}{l}} {\left( { \frac{ 1 } { 2 } + \frac{{\sqrt 5 }}{2}} \right){V_{12}} + {V_{22}} = 0}\\ {{V_{12}} – \left( {\frac{1}{2} – \frac { { \sqrt 5 } } { 2 } } \right){V_{22}} = 0} \end{array}} \right.,\;\; } \\ \\ \Rightarrow {\left\{ {\begin{array}{*{20} { l } } {\left( {\frac { 1 } { 2 } + \frac{{\sqrt 5 }}{2}} \right){V_{12}} + {V_{22}} = 0 } \\ {\left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right){V_{12}} + { V _ { 22 } } = 0} \end{array}} \right.,\;\;} \\ \\ \Rightarrow {\left ( { \frac { 1 } { 2 } + \frac { { \sqrt 5 } }{2}} \right){V_{12}} + {V_{22}} = 0 } \end {gather*} $$

با تغییر متغیر $${ V _ { 12 } } = t$$ نهایتا بردار $$V_2$$ نیز به صورت زیر بدست خواهد آمد.

$$\begin {gather*} { { V _ { 22 } } = – \left ( {\frac{1}{2} + \frac{{\sqrt 5 } } { 2 } } \right ) { V _ { 12}} } = {- \left( { \frac { 1 } { 2 } + \frac{{\sqrt 5 } } { 2 } } \right)t }\approx{ -1.62t,\;\;} \\ \\ \Rightarrow {{{\mathbf{V}_2} = \left[ {\begin{array}{*{20} { c } } { { V _ { 12 } } } \\ { { V _ { 22 } } } \end{array} } \right] } = {\left[ {\begin{array}{*{20} { c } } t \\ {-1.62t} \end{array} } \right] } = {t\left[ {\begin{array}{*{20} { c } } 1\\ {-1.62} \end{array} } \right] } } \sim{{ \left[ {\begin{array}{*{20 }{ c } } 1 \\ {-1.62} \end {array}} \right] } } \end {gather*} $$

با ترسیم بردار‌های بدست آمده و عبور دادن آن‌ها از مرکز،‌ میدان فازی سیستم خطی شده به صورت زیر بدست می‌آید.

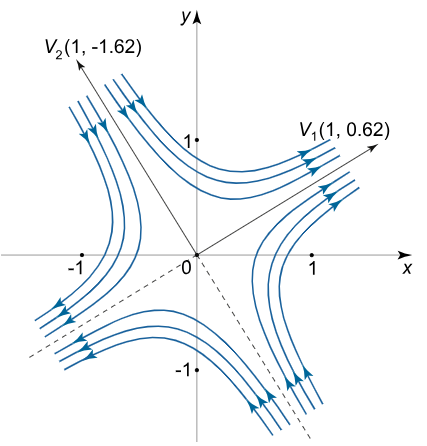
این خطوط نشان دهنده مرز‌های زین هستند. توجه داشته باشید که به منظور شناسایی مسیر کافی است تا نقطه مورد بررسی را در رابطه فوق قرار دهید. برای نمونه با قرار دادن نقطه $$\left ( { 1 , 0 } \right )$$ در بردار بدست آمده در بالا، سرعت میدان برداری در این نقطه برابر است با:

$$\large { { { \left. {\frac { { d x } } { { d t } } } \right|_{\left( {1,0} \right)}} = { e ^ { 1 + 0 } } – 1 } \approx{ 1.72 \;\;\;} } \kern-0.3pt { { { \left. {\frac { { d y } } { { d t } } } \right|_{\left ( { 1 , 0 } \right ) } } = \ln \left( {1 + 1} \right) }={ \ln 2 }\approx { 0.69}}$$

بدیهی است که مقادیر فوق نشان دهنده سرعت میدان به سمت شمال شرقی است.

^^