ممان اینرسی کره توپر و تو خالی – محاسبه به زبان ساده

لختی دورانی یا ممان اینرسی کره، معیاری برای ارزیابی نحوه توزیع جرم این شکل سه‌بعدی حول یک محور مشخص است. به عبارت دیگر، اگر یک کره را حول محور مشخصی بچرخانیم، ذرات آن در برابر شتاب زاویه‌ای، مقاومت می‌کنند. ممان اینرسی کره، مقاومت ذرات آن در برابر این شتاب را نمایش می‌دهد. لختی دورانی، به فاصله ذرات از محور دوران و جرم آن‌ها بستگی دارد. این کمیت، از ضرب جرم هر ذره کره در مربع فاصله آن ذره تا محور دوران و جمع حاصل‌ضرب‌ها محاسبه می‌شود. در این مقاله، به معرفی و اثبات فرمول‌های محاسبه ممان اینرسی کره توپر و توخالی حول محورهای گذرنده از مرکز و محورهای دلخواه می‌پردازیم. علاوه بر این، چندین مثال متنوع را نیز حل می‌کنیم.

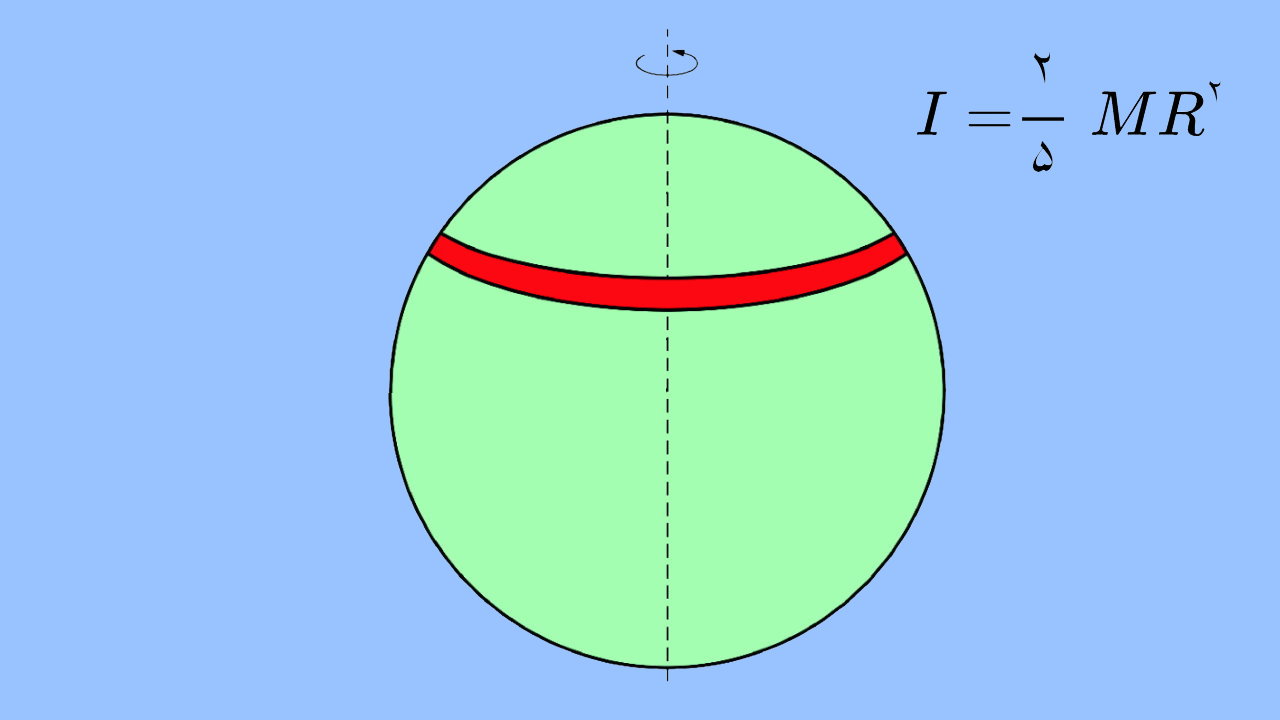
ممان اینرسی چیست ؟

لختی دورانی یا «ممان اینرسی» (Moment of Inertia)، کمیتی است که به منظور نمایش میزان مقاومت یک جسم در برابر شتاب زاویه‌ای حول یک محور دوران مشخص مورد استفاده قرار می‌گیرد. این کمیت، از مجموع حاصل‌ضرب وزن هر ذره در مربع فاصله آن تا محور دوران به دست می‌آید.

فیلم آموزش استاتیک – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

ممان اینرسی با عنوان «جرم زاویه‌ای» (Angular Mass) نیز شناخته می‌شود. تصویر زیر، مقایسه شتاب زاویه‌ای اجسام مختلف را نمایش می‌دهد. جسمی که ممان اینرسی کمتری دارد، به دلیل مقاومت پایین‌تر در برابر شتاب‌زاویه‌ای، زودتر از دیگر اجسام به انتهای مسیر می‌رسد.

فرمول گسسته ممان اینرسی عبارت است از:

$$I = \sum m _ i r _ i ^ ۲$$

این فرمول، تعریف لختی دورانی به زبان ریاضی است. همان‌طور که مشاهده می‌کنید، ممان اینرسی (I)، مجموع حاصل‌ضرب جرم هر نقطه از جسم (جرم m) در فاصله آن نقطه تا محور دوران (فاصله r) است. فرمول پیوسته ممان اینرسی به صورت زیر نوشته می‌شود:

$$I = \int r ^ ۲ dm$$

ممان اینرسی، نحوه توزیع جرم حول محور دوران را نمایش می‌دهد. در صورت تغییر محور دوران، ممان اینرسی نیز تغییر می‌کند. برای شکل‌های معروف، معمولا محور گذرنده از مرکز جرم به عنوان محور دوران در نظر گرفته می‌شود. در ادامه، به معرفی ممان اینرسی یکی از شکل‌های معروف هندسی، یعنی کره می‌پردازیم.

ممان اینرسی کره چگونه بدست می آید ؟

«کره» (Sphere)، مجموعه‌ای از نقاط در فضای سه‌بعدی است که از یک نقطه ثابت، فاصله یکسانی دارند. این شکل، معادل سه‌بعدی دایره است. بسیاری از اجسام طبیعی و مصنوعی، به شکل کره هستند. از این‌رو، آشنایی با ممان اینرسی این شکل، خالی از لطف نیست.

فیلم آموزش ایستایی (استاتیک) – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

فرمول ممان اینرسی کره توپر به صورت زیر نوشته می‌شود:

$$I = \frac { ۲ } { ۵ } M R ^ ۲$$

• I: ممان اینرسی کره
• M: جرم کره
• R: شعاع کره

به خاطر داشته باشید که فرمول بالا، ممان اینرسی کره حول محور گذرنده از مرکز آن (محور منطبق بر روی قطر) را نمایش می‌دهد. اگر محور مماس بر سطح کره را در نظر بگیریم، فرمول ممان اینرسی کره به شکل زیر تغییر می‌کند:

$$I = \frac { ۷ } { ۵ } M R ^ ۲$$

• I: ممان اینرسی کره حول محور مماس بر سطح
• M: جرم کره
• R: شعاع کره

فرمول بالا، بر اساس قضیه محورهای موازی به دست آمده است. در بخش‌های بعدی، به معرفی این قضیه خواهیم پرداخت.

یکای ممان اینرسی کره چیست ؟

ممان اینرسی کره در سیستم یکاهای بین‌المللی SI با یکای کیلوگرم در متر مربع (kg.m^۲) بیان می‌شود. یکای این کمیت در سیستم آمریکایی برابر با پوند فوت در مربع ثانیه (lbf.ft.s^۲) است.

ممان اینرسی دایره چیست ؟

کره، یکی از شکل‌های مرتبط با دایره است. اگر کره را بر روی صفحه گذرنده از مرکز آن برش دهیم، سطح برش به شکل دایره خواهد بود. ممان اینرسی دایره توپر از رابطه زیر به دست می‌آید:

$$I = \frac { \pi } { ۴ } R ^ ۴$$

• I: ممان اینرسی دایره توپر
• π: عدد پی
• R: شعاع دایره

برای سطوح، کمیتی با عنوان «ممان اینرسی سطح» (Area Moment of Inertia) تعریف می‌شود. این کمیت، توزیع هندسی نقاط یک سطح، نسبت به محور دوران مشخص را نمایش می‌دهند. به همین دلیل، در فرمول بالا، خبری از پارامتر M (جرم) نیست. اگر دایره را برابر با یک دیسک (دایره‌ای با ضخامت کم) در نظر بگیریم، ممان اینرسی آن حول محور گذرنده از مرکز و عمود بر سطح به صورت زیر محاسبه می‌شود:

$$I = \frac { ۱ } { ۲ } M R ^ ۲$$

M، جرم دیسک است. فرمول بالا، در اثبات فرمول ممان اینرسی کره توپر مورد استفاده قرار می‌گیرد.

مثال ۱: محاسبه ممان اینرسی کره توپر

لختی دورانی کره توپری به شعاع ۰/۱۲ متر و جرم ۵۵ کیلوگرم را به دست بیاورید.

فرمول لختی دورانی کره توپر عبارت است از:

$$I = \frac { ۲ } { ۵ } M R ^ ۲$$

• I: ممان اینرسی کره
• M: جرم کره برابر با ۵۵ کیلوگرم
• R: شعاع کره برابر با ۰/۱۲ متر

مقادیر معلوم را در فرمول بالا قرار می‌دهیم:

$$I = \frac { ۲ } { ۵ } \times ۵۵ \times ۰/۱۲ ^ ۲$$

$$I = ۲ \times ۱۱ \times ۰/۰۱۴۴$$

$$I = ۲۲ \times ۰/۰۱۴۴$$

$$I = ۰/۳۱۶۸$$

ممان اینرسی کره توپر، برابر با ۰/۳۱۶۸ کیلوگرم در متر مربع (kg.m^۲) است.

اثبات فرمول ممان اینرسی کره توپر

اثبات فرمول ممان اینرسی کره توپر، طی دو مرحله زیر انجام می‌شود:

1. در نظر گرفتن یک برش از کره با ضخامت بسیار کوچک (یک استوانه با ارتفاع بسیار کم یا یک دیسک دایره‌ای)
2.  جمع ممان‌های اینرسی تمام برش‌های کره در راستای یک محور مشخص

فیلم آموزش فیزیک پایه ۱ – مفاهیم پایه + حل مثال در فرادرس

کلیک کنید

تصویر زیر، کره‌ای به شعاع R و جرم M را نمایش می‌دهد. یک المان کوچک از این کره را در نظر بگیرید. ضخامت این المان (dx) به اندازه‌ای کم است که می‌توان آن را به عنوان یک استوانه با ارتفاع جزئی یا یک دیسک دایره‌ای حساب کرد.

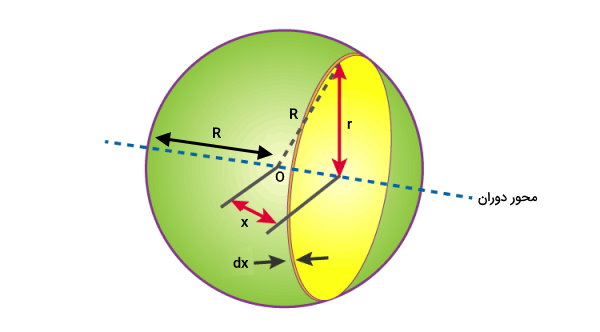
می‌خواهیم فرمول ممان اینرسی کره بالا حول محور مرکزی را اثبات کنیم. این فرمول عبارت است از:

$$I _ s = \frac { ۲ } { ۵ } M R ^ ۲$$

• I_s: ممان اینرسی کره توپر
• M_s: جرم کره
• R_s: شعاع کره

برای اثبات فرمول بالا، باید مجموع ممان‌های اینرسی برش‌های نازک را به دست بیاوریم. این برش‌ها به شکل دیسک توپر هستند. فرمول ممان اینرسی دیسک دایره‌ای توپر به صورت زیر نوشته می‌شود:

$$I _ { d } = \frac { ۱ } { ۲ } M _ d R _ d ^ ۲$$

• I_d: ممان اینرسی دیسک دایره‌ای توپر
• M_d: جرم دیسک
• R_d: شعاع دیسک

شعاع برش‌های کره، در بازه ۰ تا R قرار دارد. برای یک برش دلخواه، این شعاع را برابر با r در نظر می‌گیریم. جرم این برش، مقدار کوچکی از جرم کل کره است. این مقدار را با d_m نمایش می‌دهیم. به این ترتیب، ممان اینرسی یک برش از کره با استفاده از فرمول زیر به دست می‌آید:

$$d I = \frac { ۱ } { ۲ } r ^ ۲ d m$$

• d_I: ممان اینرسی جزئی کره توپر (ممان اینرسی یک برش نازک از کره)
• d_m: جرم جزئی کره (جرم یک برش نازک از کره)
• r: شعاع یک برش از کره

جرم برش کره، با از رابطه زیر محاسبه می‌شود:

$$d m = \rho d v$$

• d_m: جرم برش کره
• ρ: چگالی برش کره
• d_v: حجم جزئی کره (حجم برش نازک)

فرمول محاسبه حجم برش عبارت است از:

$$d v = \pi r ^ ۲ d x$$

• d_v: حجم برش
• r: شعاع برش
• d_x: ضخامت جزئی برش

رابطه بالا را در رابطه جرم قرار می‌‌دهیم:

$$d m = \rho \pi r ^ ۲ d x$$

با قرار دادن این رابطه در فرمول ممان اینرسی، خواهیم داشت:

$$dI = \frac { ۱ } { ۲ } r ^ ۲ \rho \pi r ^ ۲ d x$$

$$d I = \frac { ۱ } { ۲ } \rho \pi r ^ ۴ d x$$

قدم بعدی اثبات فرمول ممان اینرسی کره توپر، نوشتن r بر حسب متغیر x است. فاصله مرکز کره تا مرکز دیسک، برابر با x است. اگر بالاترین نقطه دیسک را به مرکز آن و مرکز کره وصل کنیم، یک مثلث قائم‌الزاویه مانند تصویر زیر به وجود می‌آید.

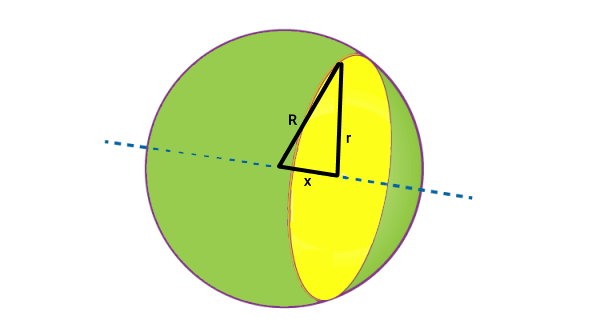
بر اساس قضیه فیثاغورس در مثلث‌های قائم‌الزاویه، شعاع کره برابر است با:

$$R ^ ۲ = r ^ ۲ - x ^ ۲$$

• R: شعاع کره
• r: شعاع دیسک
• x: فاصله مرکز کره تا مرکز دیسک

فرمول بالا را بر حسب r بازنویسی می‌کنیم:

$$r ^ ۲ = R ^ ۲ - x ^ ۲$$

به جای r در فرمول ممان اینرسی دیسک، سمت راست رابطه بالا را قرار می‌دهیم:

$$d i = \frac { ۱ } { ۲ } \rho \pi ( R ^ ۲ - x ^ ۲ ) ^ ۲ d x$$

اگر ممان اینرسی تمام برش‌های کره در بازه R تا R- را با هم جمع کنیم، ممان اینرسی کره به دست می‌آید. به عبارت دیگر، با انتگرال‌گیری از دو طرف رابطه بالا در بازه R تا R-، به ممان اینرسی کره می‌رسیم:

$$\int _ { - R } ^ { R } d I = \int _ { - R } ^ { R }\frac { ۱ } { ۲ } \rho \pi ( R ^ ۲ - x ^ ۲ ) ^ ۲ d x$$

در طرف چپ رابطه بالا، انتگرال dI قرار دارد. جواب این انتگرال در بازه R تا R-، برابر با I است. به این ترتیب، با حل انتگرال طرف راست، به رابطه زیر می‌رسیم:

$$I = \frac { ۸ } { ۱۵ } \rho \pi R ^ ۵$$

می‌دانیم که چگالی کره (ρ)، از تقسیم جرم (M) بر حجم (V)، به دست می‌آید. بنابراین:

$$\rho = \frac { M } { \frac { ۴ } { ۳ } \pi R ^ ۳ }$$

به جای ρ در فرمول به دست آمده برای I، طرف راست رابطه بالا را قرار می‌دهیم:

$$I = \frac { ۸ } { ۱۵ } \times\frac { M } { \frac { ۴ } { ۳ } \pi R ^ ۳ }\pi R ^ ۵$$

$$I = \frac { ۸ M } { ۱۵ \times \frac { ۴ } { ۳ } } R ^ ۲$$

$$I = \frac { ۸ M } { ۵ \times ۴ } R ^ ۲$$

$$I = \frac { ۲ M } { ۵ } R ^ ۲$$

$$I = \frac { ۲ } { ۵ } M R ^ ۲$$

این رابطه، همان فرمول ممان اینرسی کره توپر است.

قضیه محورهای موازی در ممان اینرسی کره توپر

ممان اینرسی یک جسم، حول محوری موازی با محور گذرنده از مرکز جرم آن، از فرمول زیر به دست می‌آید:

$$I = I _ { cm } + M d ^ ۲$$

پارامترهای موجود در این فرمول، عبارت هستند از:

• I: ممان اینرسی حول محور موازی با محور گذرنده از مرکز جرم
• I_cm: ممان اینرسی حول محور گذرنده از مرکز جرم
• M: جرم
• d: فاصله محور دوران با محور گذرنده از مرکز جرم

فیلم آموزش فیزیک پایه 1 – مرور و حل تست در فرادرس

کلیک کنید

رابطه بالا، با عنوان «قضیه محورهای موازی» (Parallel Axis Theorem) شناخته می‌شود. بر اساس این قضیه، ممان اینرسی کره توپر حول محوری موازی با محور گذرنده از مرکز جرم آن برابر است با:

$$I = \frac { ۲ } { ۵ } M R ^ ۲ + M d ^ ۲$$

اگر محور موازی، مماس بر سطح کره باشد، فاصله آن تا محور گذرنده از مرکز جرم، برابر با شعاع کره (R) خواهد بود.

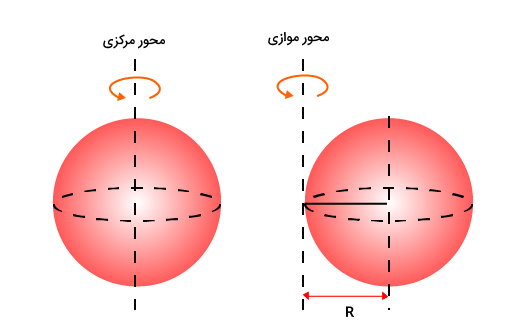
در این حالت، برای ممان اینرسی کره حول محور موازی با محور مرکزی خواهیم داشت:

$$d = R$$

$$I = \frac { ۲ } { ۵ } M R ^ ۲ + M R ^ ۲$$

$$I = \frac { ۲ M R ^ ۲ } { ۵ } + \frac { ۵ M R ^ ۲ } { ۵ }$$

$$I = \frac { ۲ M R ^ ۲ + ۵ M R ^ ۲ } { ۵ }$$

$$I = \frac { ۷ M R ^ ۲ } { ۵ }$$

$$I = \frac { ۷ } { ۵ }M R ^ ۲$$

همان‌طور که مشاهده می‌کنید، ممان اینرسی کره توپر حول محور مماس بر سطح آن، بزرگ‌تر از ممان اینرسی کره توپر حول محور مرکزی است. نسبت این دو برابر است با:

$$\frac { I } { I _ { c m }} = \frac { \frac { ۷ } { ۵ } M R ^ ۲ } { \frac { ۲ } { ۵ } M R ^ ۲ }$$

$$\frac { I } { I _ { c m }} = \frac { \frac { ۷ } { ۵ } } { \frac { ۲ } { ۵ }}$$

$$\frac { I } { I _ { c m }} = \frac { ۷ } { ۲ }$$

$$\frac { I } { I _ { c m }} = ۳/۵$$

با تغییر مکان محور دوران از مرکز به سطح، ممان اینرسی کره، ۳/۵ برابر می‌شود. بنابراین، هر چه محور دوران از مرکز جرم فاصله داشته باشد، ممان اینرسی بزرگ‌تر خواهد بود.

مثال ۲: محاسبه لختی دورانی کره حول محور دلخواه

کره توپری به جرم ۶۰ کیلوگرم و شعاع ۰/۱۵ متر را در نظر بگیرید. این کره را حول محوری موازی با یکی از محورهای گذرنده از مرکز آن دوران می‌دهیم. اگر فاصله مرکز کره تا محور دوران، به اندازه دو برابر شعاع باشد، ممان اینرسی چقدر خواهد بود؟

ممان اینرسی حول محوری موازی با محور مرکزی از رابطه زیر به دست می‌آید:

$$I = I _ { cm } + M d ^ ۲$$

پارامترهای موجود در این فرمول، عبارت هستند از:

• I: ممان اینرسی حول محور موازی با محور گذرنده از مرکز جرم
• I_cm: ممان اینرسی حول محور گذرنده از مرکز جرم
• M: جرم کره برابر با ۶۰ کیلوگرم
• d: فاصله محور دوران با محور گذرنده از مرکز جرم برابر با ۰/۳ متر (دو برابر شعاع کره)

در رابطه بالا، فقط مقدار ممان اینرسی حول محور مرکزی را نداریم. این پارامتر با استفاده از فرمول زیر محاسبه می‌شود:

$$I _ { c m } = \frac { ۲ } { ۵ } M R ^ ۲$$

$$I _ { c m } = \frac { ۲ } { ۵ } \times ۶۰ \times ۰/۱۵ ^ ۲$$

$$I _ { c m } = ۲ \times ۱۲ \times ۰/۰۲۲۵$$

$$I _ { c m } = ۲۴ \times ۰/۰۲۲۵$$

$$I _ { c m } = ۰/۵۴$$

به این ترتیب، داریم:

$$I = I _ { cm } + M d ^ ۲$$

$$I = ۰/۵۴ + ( ۶۰ \times ۰/۰۹ )$$

$$I = ۰/۵۴ + ۵/۴$$

$$I = ۵/۹۴$$

در نتیجه، ممان اینرسی حول محور دلخواه برابر با ۵/۹۴ کیلوگرم در متر مربع است.

ممان اینرسی کره توخالی چگونه بدست می آید ؟

ممان اینرسی کره توخالی یا پوسته کروی حول محور گذرنده از مرکز آن، توسط فرمول زیر به دست می‌آید:

$$I = \frac { ۲ } { ۳ } M R ^ ۲$$

• I: ممان اینرسی کره توخالی حول محور مرکزی
• M: جرم کره
• R: شعاع کره

اگر محور دوران، مماس بر سطح کره توخالی باشد، فرمول ممان اینرسی به صورت زیر تغییر می‌کند:

$$I = \frac { ۵ } { ۳ } M R ^ ۲$$

ممان اینرسی حلقه چیست ؟

«حلقه» (Ring)، یک دایره توخالی است. اگر کره توخالی را در راستای صفحه‌ای عمود بر محور مرکزی برش دهیم، سطح برش به شکل حلقه درمی‌آید.

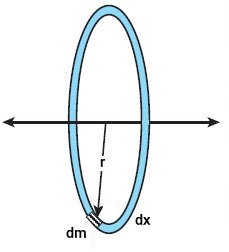
ممان اینرسی سطح حلقه برابر است با:

$$I = \frac { \pi }{ ۴ } \left ( R _ ۲ ^ ۴ - R _ ۱ ^ ۴ \right )$$

• I_x: گشتاور دوم سطح حلقه دایره‌ای نسبت به محور مرکزی
• R_۱: شعاع داخلی سطح حلقه
• R_۲: شعاع خارجی سطح حلقه

اگر یک ضخامت جزئی برای حلقه در نظر بگیریم (حلقه را به صورت یک استوانه توخالی با ارتفاع کم در نظر بگیریم)، ممان اینرسی جرم آن حول محور عمود بر مرکز سطح دربرگیرنده آن (محور تقارن)، با استفاده از فرمول زیر محاسبه می‌شود:

$$I = M R ^ ۲$$

• I: ممان اینرسی حلقه حول محور مرکزی
• M: جرم حلقه
• R: شعاع خارجی حلقه

از رابطه بالا در اثبات فرمول لختی دورانی کره توخالی استفاده خواهیم کرد.

مثال ۳: مقایسه ممان اینرسی کره توپر و توخالی

دو جسم کروی با مشخصات زیر را در نظر بگیرید:

1. کره توپر
   • شعاع ۱۰ سانتی‌متر
   • جرم ۲۰۰ گرم
2. کره توخالی
   • شعاع ۷ سانتی‌متر
   • جرم ۲۳۰ گرم

ممان اینرسی کدامیک از اجسام بالا حول محور مرکزی‌شان بیشتر از ممان اینرسی دیگری است؟

پیش از شروع محاسبات، به یکاهای داده شده توجه داشته باشید. اگر بخواهیم ممان‌های اینرسی را بر اساس یکاهای رایج و استاندارد به دست بیاوریم، ابتدا این یکاها را به متر و کیلوگرم تبدیل کنیم:

1. کره توپر
   • شعاع ۰/۱ متر
   • جرم ۰/۲ کیلوگرم
2. کره توخالی
   • شعاع ۰/۰۷ متر
   • جرم ۰/۲۳ کیلوگرم

لختی دورانی کره توپر عبارت است از:

$$I = \frac { ۲ } { ۵ } M R ^ ۲$$

• I: ممان اینرسی کره
• M: جرم کره برابر با ۰/۲
• R: شعاع کره برابر با ۰/۱

$$I = \frac { ۲ } { ۵ } \times ۰/۲ \times ۰/۱ ^ ۲$$

$$I = \frac { ۰/۴ } { ۵ } \times ۰/۰۱$$

$$I = ۰/۰۸ \times ۰/۰۱$$

$$I = ۸ \times ۱۰ ^ { - ۴ }$$

ممان اینرسی جسم کروی توپر برابر با $$۸ \times ۱۰ ^ { - ۴ } kgm ^ ۲$$ است. لختی دورانی کره توسط رابطه زیر محاسبه می‌شود:

$$I = \frac { ۲ } { ۳ } M R ^ ۲$$

• I: ممان اینرسی کره توخالی حول محور مرکزی
• M: جرم کره توخالی برابر با ۰/۲۳ کیلوگرم
• R: شعاع کره برابر با ۰/۰۷ متر

$$I = \frac { ۲ } { ۳ } \times ۰/۲۳ \times ۰/۰۰۴۹$$

$$I = \frac { ۲ } { ۳ } \times ۰/۰۰۱۱۲۷$$

$$I = \frac { ۰/۰۰۲۲۵۴ } { ۳ }$$

$$I = ۷/۵۳ \times ۱۰ ^ { - ۴ }$$

ممان اینرسی جسم کروی توخالی برابر با $$۷/۵۳ \times ۱۰ ^ { - ۴ }$$ است. بنابراین، در این مثال، کره توپر ممان اینرسی بیشتری نسبت به کره توخالی دارد. توجه داشته باشید که در صورت برابر بودن جرم و ابعاد هر دو کره، ممان اینرسی جسم توخالی، بیشتر می‌شد. این مثال، مقایسه بین ممان‌های اینرسی را می‌خواهد. بنابراین، به دلیل یکسان بودن یکاها، حل مسئله با یکاهای قبلی نیز کفایت می‌کرد. با این وجود، برای نمایش استاندارد ممان‌ها، یکاهای پارامترهای آن‌ها را تغییر دادیم.

اثبات فرمول ممان اینرسی کره توخالی

یک کره توخالی به جرم M، شعاع خارجی R را در نظر بگیرید. فرمول ممان اینرسی این شکل حول محور گذرنده از مرکز جرم آن برابر است با:

$$I = \frac { ۲ } { ۳ } M R ^ ۲$$

برای اثبات فرمول بالا، یک المان کوچک از کره توخالی در راستای صفحه‌ای عمود بر محور مرکزی را در نظر می‌گیریم. این المان، حلقه‌ای به ضخامت dx و شعاع r است که مرکز آن، در فاصله x از مرکز دایره قرار دارد.

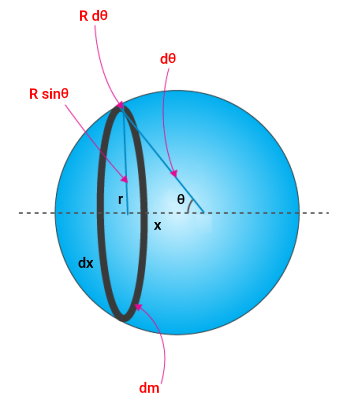
فرمول ممان اینرسی حلقه بالا به صورت زیر نوشته می‌شود:

$$I = m r ^ ۲$$

• I: ممان اینرسی حلقه‌ای از کره
• m: جرم حلقه
• r: شعاع حلقه

ممان اینرسی کره توخالی، مجموع ممان‌های اینرسی تمام حلقه‌های تشکیل‌دهنده آن است. از این‌رو، برای به‌دست آوردن این ممان، می‌توانیم از فرم دیفرانسیلی فرمول بالا استفاده کنیم:

$$d I = r ^ ۲ d m$$

• dI: ممان اینرسی المان حلقه‌‌ای کره توخالی
• r: شعاع المان حلقه‌ای کره توخالی
• dm: جرم المان حلقه‌ای کره توخالی

کره توخالی، یک پوسته یا سطح بسته است. چگالی این سطح از رابطه زیر به دست می‌آید:

$$\rho = \frac { M } { A }$$

• ρ: چگالی کره توخالی
• M: جرم کره توخالی
• A: سطح رویه کره توخالی

چگالی المان حلقه‌ای کره توخالی و چگالی المان حلقه‌ای آن، با یکدیگر برابرند. بنابراین:

$$\rho = \frac { d m } { d A }$$

• ρ: چگالی کره توخالی
• dm: جرم المان حلقه‌ای کره توخالی
• dA: مساحت رویه المان حلقه‌ای کره توخالی

به این ترتیب داریم:

$$\frac { M } { A } = \frac { d m } { d A }$$

رابطه بالا را بر حسب dm بازنویسی می‌کنیم:

$$d m = \frac { M } { A } d A$$

سطح کل رویه کره از رابطه زیر به دست می‌آید:

$$A = ۴ \pi R ^ ۲$$

مساحت رویه المان حلقه‌ای کره توخالی نیز عبارت است از:

$$d A = ۲ \pi r R d \theta$$

عبارت $$۲ \pi r$$، محیط حلقه (فرمول محیط دایره) و عبارت $$R d$$، ضخامت حلقه (فرمول طول کمان دایره) را نمایش می‌دهد. ضرب محیط در ضخامت حلقه، برابر با مساحت آن است. اکنون، شکل کره توخالی و یکی از المان‌های حلقه‌ای آن را در نظر بگیرید. در این شکل، می‌توانیم یک مثلث قائم‌الزاویه با وتر R و ساق‌های r و x ایجاد کنیم. اگر زاویه راس منطبق بر مرکز کره، برابر با θ باشد، بر اساس قوانین مثلثات، خواهیم داشت:

$$\sin \theta = \frac { r } { R }$$

نسبت مثلثاتی بالا را بر حسب r بازنویسی می‌کنیم:

$$r = R \sin \theta$$

رابطه r را درون فرمول به دست آمده برای dA قرار می‌دهیم:

$$d A = ۲ \pi R ^ ۲ \sin \theta d \theta$$

با جایگذاری رابطه dA در فرمول dm، به رابطه زیر می‌رسیم:

$$d m = \frac { M } { A } ( ۲ \pi R ^ ۲ \sin \theta d \theta )$$

$$d m = \frac { M } { ۴ \pi R ^ ۲ } ( ۲ \pi R ^ ۲ \sin \theta d \theta )$$

$$d m = \frac { M } { ۲ } \sin \theta d \theta$$

اکنون، به جای dm در فرمول dI، سمت راست رابطه بالا را نوشته و به جای r، عبارت $$R \sin \theta$$ را می‌نویسیم:

$$d I = ( R \sin \theta ) ^ ۲ ( \frac { M } { ۲ } \sin \theta d \theta )$$

$$d I = \frac { M R ^ ۲ } { ۲ } \sin ^ ۳ \theta d \theta$$

با انتگرال‌گیری از این رابطه بالا نسبت به θ در بازه ۰ تا π، ممان اینرسی کره به دست می‌آید:

$$\int _ { ۰ } ^{ \pi } d I = \int _ { ۰ } ^{ \pi } \frac { M R ^ ۲ } { ۲ } \sin ^ ۳ \theta d \theta$$

$$I = \frac { M R ^ ۲ } { ۲ } \int _ { ۰ } ^{ \pi } \sin ^ ۳ \theta d \theta$$

انتگرال سینوس به توان سه به صورت زیر محاسبه می‌شود:

$$\sin ^ ۳ \left ( \theta \right ) = \sin ^ ۲ \left ( \theta \right ) \sin \left ( \theta \right )$$

$$\sin ^ ۲ \left ( \theta \right ) = ۱ - \cos ^ ۲ \left ( \theta \right )$$

$$\sin ^ ۳ \left ( \theta \right ) = \left ( ۱ - \cos ^ ۲ \left ( \theta \right ) \right ) \sin \left ( \theta \right )$$

$$\int \sin ^ ۳ \left ( \theta \right ) d \theta = \int \left ( ۱ - \cos ^ ۲ \left ( \theta \right ) \right ) \sin \left ( \theta \right ) d \theta$$

برای ساده شدن فرآیند انتگرال‌گیری، تغییر متغیرهای زیر را اعمال می‌کنیم:

$$u = \cos \left ( \theta \right )$$

$$d u = - \sin \left ( \theta \right ) d \theta$$

$$\int \sin ^ ۳ \left ( \theta \right ) d \theta = \int \left ( ۱ - u ^ ۲ \right ) ( - d u )$$

$$\int \sin ^ ۳ \left ( \theta \right ) d \theta = - \int \left ( ۱ - u ^ ۲ \right ) ( d u )$$

$$\int \sin ^ ۳ \left ( \theta \right ) d \theta = - \int ( d u - u ^ ۲ d u )$$

$$\int \sin ^ ۳ \left ( \theta \right ) d \theta = - \int d u + \int u ^ ۲ d u$$

$$\int \sin ^ ۳ \left ( \theta \right ) d \theta = - u + \frac { u ^ ۳ }{ ۳ }$$

پس از بازگرداندن متغیرهای تغییر یافته به عبارت‌های اولیه، خواهیم داشت:

$$\int \sin ^ ۳ \left ( \theta \right ) d \theta = - \cos ( \theta ) + \frac { \cos ^ ۳ ( \theta ) }{ ۳ }$$

مقدار عددی این انتگرال در بازه ۰ تا π برابر است با:

$$\int _ { ۰ } ^ { \pi } \sin ^ ۳ \left ( \theta \right ) d \theta = \left [ - \cos ( \theta ) + \frac { \cos ^ ۳ ( \theta ) }{ ۳ } \right ] _ { ۰ } ^ { \pi }$$

$$\int _ { ۰ } ^ { \pi } \sin ^ ۳ \left ( \theta \right ) d \theta = \left ( - \cos ( \pi ) + \frac { \cos ^ ۳ ( \pi ) }{ ۳ } \right ) - \left ( - \cos ( ۰ ) + \frac { \cos ^ ۳ ( ۰ ) }{ ۳ } \right )$$

$$\int _ { ۰ } ^ { \pi } \sin ^ ۳ \left ( \theta \right ) d \theta = \left ( - ( - ۱ ) + \frac { - ۱ }{ ۳ } \right ) - \left ( - ۱ + \frac { ۱ }{ ۳ } \right )$$

$$\int _ { ۰ } ^ { \pi } \sin ^ ۳ \left ( \theta \right ) d \theta = \left ( ۱ - \frac { ۱ }{ ۳ } \right ) - \left ( - ۱ + \frac { ۱ }{ ۳ } \right )$$

$$\int _ { ۰ } ^ { \pi } \sin ^ ۳ \left ( \theta \right ) d \theta = \left ( \frac { ۲ }{ ۳ } \right ) - \left ( - \frac { ۲ }{ ۳ } \right )$$

$$\int _ { ۰ } ^ { \pi } \sin ^ ۳ \left ( \theta \right ) d \theta = \frac { ۲ }{ ۳ } + \frac { ۲ }{ ۳ }$$

$$\int _ { ۰ } ^ { \pi } \sin ^ ۳ \left ( \theta \right ) d \theta = \frac { ۴ }{ ۳ }$$

به این ترتیب داریم:

$$I = \frac { M R ^ ۲ } { ۲ } \int _ { ۰ } ^{ \pi } \sin ^ ۳ \theta d \theta$$

$$I = \frac { M R ^ ۲ } { ۲ } \times \frac { ۴ }{ ۳ }$$

$$I = \frac { ۲ }{ ۳ } M R ^ ۲$$

در نتیجه، فرمول ممان اینرسی کره توخالی اثبات شد. در صورت تمایل به آشنایی بیشتر با نحوه محاسبه انتگرال توابع مثلثاتی، مطالعه مطلب «انتگرال توابع مثلثاتی — از صفر تا صد» را به شما پیشنهاد می‌کنیم.

قضیه محورهای موازی در ممان اینرسی کره توخالی

قضیه محورهای موازی به صورت زیر نوشته می‌شود:

$$I = I _ { cm } + M d ^ ۲$$

• I: ممان اینرسی حول محور موازی با محور گذرنده از مرکز جرم
• I_cm: ممان اینرسی حول محور گذرنده از مرکز جرم
• M: جرم
• d: فاصله محور دوران با محور گذرنده از مرکز جرم

به عنوان مثال، اگر بخواهیم ممان اینرسی کره توخالی حول محور مماس بر سطح رویه آن را به دست بیاوریم، از این قضیه استفاده می‌کنیم.

فیلم آموزش مکانیک تحلیلی 2 – جامع و کاربردی در فرادرس

کلیک کنید

در این حالت، فاصله محور دوران (محور مماس بر سطح کره) تا محور مرکزی، برابر با شعاع کره (R) است. بنابراین، داریم:

$$I = I _ { cm } + M R ^ ۲$$

ممان اینرسی کره توخالی ممان اینرسی حول محور گذرنده از مرکز جرم برابر است با:

$$I _ c = \frac { ۲ }{ ۳ } M R ^ ۲$$

به این ترتیب:

$$I = \frac { ۲ }{ ۳ } M R ^ ۲ + M R ^ ۲$$

$$I = \frac { ۲ M R ^ ۲ }{ ۳ } + \frac { ۳ M R ^ ۲ } { ۳ }$$

$$I = \frac { ۲ M R ^ ۲ + ۳ M R ^ ۲ } { ۳ }$$

$$I = \frac { ۵ M R ^ ۲ } { ۳ }$$

$$I = \frac { ۵ } { ۳ } M R ^ ۲$$

همان‌طور که مشاهده می‌کنید، ممان اینرسی جسم با فاصله گرفتن محور دوران از محور مرکزی، افزایش می‌یابد. به عنوان مثال، در اینجا، ممان اینرسی حول محور مماس بر سطح، پنج‌سوم ممان اینرسی حول محور مرکزی است.

مثال ۴: محاسبه ممان اینرسی پوسته کروی حول محور دلخواه

لختی دورانی یک کره توخالی حول محور گذرنده از مرکز جرم آن برابر با ۰/۱۸ کیلوگرم در متر مربع بوده و لختی دورانی آن حول محوری موازی با محور مرکزی برابر با ۰/۴۵ کیلوگرم در متر مربع است. آیا محور موازی با محور مرکزی، از داخل کره عبور می‌کند؟

ممان اینرسی کره توخالی حول محور مماس با سطح آن (محور گذرنده از یک نقطه منفرد بر روی سطح کره) برابر است با:

$$I = \frac { ۵ } { ۳ } M R ^ ۲$$

با دور شدن محور دوران از محور مرکزی، مقدار ممان اینرسی افزایش می‌یابد. بنابراین، اگر مقدار ممان اینرسی حول محور دلخواه و موازی با محور مرکزی، کمتر از I باشد، این محور دلخواه از درون کره توپر عبور خواهد کرد. از آنجایی که اندازه شعاع (R) و جرم (M) کره را نداریم، محاسبه I به صورت مستقیم و توسط فرمول بالا امکان‌پذیر نیست. بنابراین، از نسبت I به I_cm، استفاده می‌کنیم. I_cm، ممان اینرسی حول محور مرکزی کره توخالی است که از رابطه زیر به دست می‌آید:

$$I _ { c m } = \frac { ۲ } { ۳ } M R ^ ۲$$

نسبت I به I_cm برابر است با:

$$\frac { I }{ I _ { c m } } = \frac { \frac { ۵ } { ۳ } M R ^ ۲ }{ \frac { ۲ } { ۳ } M R ^ ۲ }$$

$$\frac { I }{ I _ { c m } } = \frac { \frac { ۵ } { ۳ } }{ \frac { ۲ } { ۳ } }$$

$$\frac { I }{ I _ { c m } } = \frac { ۵ }{ ۲ }$$

$$\frac { I }{ I _ { c m } } = ۲/۵$$

با توجه به اطلاعات مسئله، I_cm برابر با ۰/۱۸ کیلوگرم در متر مربع است. از این‌رو، داریم:

$$\frac { I }{ ۰/۱۸ } = ۲/۵$$

$$I = ۲/۵ \times ۰/۱۸$$

$$I = ۰/۴۵$$

ممان اینرسی حول محور دلخواه و موازی با محور مرکزی با مقدار به دست آمده از نسبت بالا برابر شد. در نتیجه، این محور، مماس سطح کره توخالی است و از درون آن عبور نمی‌کند.

سوالات مرتبط با ممان اینرسی کره

در این بخش، به برخی از پرتکرارترین سوالات در رابطه با ممان اینرسی کره به طور خلاصه پاسخ می‌دهیم.

تعریف ممان اینرسی کره چیست ؟

ممان اینرسی یا لختی دورانی کره، معیاری است که مقاومت کره در برابر شتاب زاویه‌ای و نحوه توزیع ذرات آن را نسبت به یک محور مشخص نمایش می‌دهد.

ممان اینرسی کره چگونه محاسبه می شود ؟

ممان اینرسی کره از ضرب جرم هر ذره در مربع فاصله آن ذره تا محور دوران و جمع حاصل این ضرب‌ها محاسبه می‌شود.

فرمول ممان اینرسی کره توپر چیست ؟

فرمول ممان اینرسی کره توپر، برابر با دو-پنجم حاصل‌ضرب جرم در مربع شعاع آن (I = ۳/۵ MR^۲) است.

فرمول ممان اینرسی کره توپر توخالی چیست ؟

فرمول ممان اینرسی کره توخالی، برابر با دو-سوم حاصل‌ضرب جرم در مربع شعاع آن (I = ۲/۳ MR^۲) است.

کمترین ممان اینرسی کره حول کدام محور دوران است ؟

کمترین ممان اینرسی کره، حول محور دوران گذرنده از مرکز جرم آن است.

رابطه بین ممان اینرسی کره با موقعیت محور دوران چگونه است ؟

هر چه محور دوران از مرکز کره فاصله داشته باشد، ممان اینرسی کره حول آن محور بیشتر می‌شود.