مساحت مربع چگونه بدست می آید؟ + فیلم آموزشی و حل تمرین و مثال
مساحت مربع برابر «طول یک ضلع ضربدر خودش» است. البته روشهای مختلفی برای اندازهگیری سطح محدودههای مربعی شکل وجود دارند. یکی از این روشها، تعیین قطر مربع و استفاده از قضیه فیثاغورس است. در این مقاله از مجله فرادرس، روشهای محاسبه مساحت مربع را به همراه چندین مثال کاربردی آموزش میدهیم.


فیلم آموزشی محاسبه مساحت مربع
مساحت مربع چیست ؟
مساحت مربع، معیاری برای تعیین سطح درون محدوده ضلعهای مربع است.
تصویر زیر، یک مربع (ضلعهای سیاه رنگ) و سطح درون آن (بخش رنگی) را نمایش میدهد.

رابطه مربع با مستطیل چیست؟
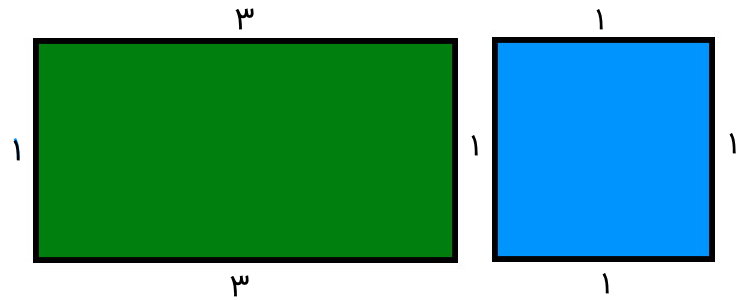
مربع، یکی از شکلهای چند ضلعی است که از چهار ضلع و چهار راس تشکیل میشود. این شکل، شباهت زیادی به مستطیل دارد. در واقع، مربع، یکی از حالتهای خاص مستطیل به شمار میرود. در این چهار ضلعی، اندازه تمام ضلعها با هم برابر است؛ در صورتی که در مستطیل، ضلعهای رو به رویی دارای اندازه برابر هستند.
مساحت مربع چگونه به دست می آید ؟
مساحت مربع، از ضرب طول یک ضلع در خودش به دست میآید. به همین دلیل، برای محاسبه مساحت این شکل هندسی، ابتدا باید طول یکی از ضلعهای آن را تعیین کرد.
فرمول مساحت مربع را میتوان به صورت زیر نوشت:
خودش یک ضلع = مساحت مربع
مثال: تعیین مساحت با طول
مربعی با طول 6 را در نظر بگیرید. مساحت این مربع چقدر است؟
مطابق با تعریف مساحت مربع، داریم:
خودش یک ضلع = مساحت
طول ضلع مربع در صورت سوال برابر 6 است. این مقدار را در رابطه بالا قرار میدهیم:
6 6 = مساحت
36 = مساحت
مساحت مربع مورد سوال برابر 36 است.
علامت ریاضی مساحت چیست؟
در ریاضیات، مساحت مربع و اکثر شکلهای هندسی، با حرف انگلیسی A نشان داده میشود. این حرف، ابتدای کلمه «Area» به معنی «مساحت» است. حرف انگلیسی a نیز معمولا به منظور نمایش ضلع مربع مورد استفاده قرار میگیرد.
فرمول مساحت مربع چیست؟
مساحت مربع به صورت جبری برابر است با:
به عبارت دیگر، مساحت مربع برابر یک ضلع به توان دو است.
واحد اندازه گیری مساحت چیست؟
در سیستم بین المللی، مساحت مربع با یکا یا واحد میلیتر مربع، سانتیمتر مربع، متر مربع و غیره بیان میشود. در ریاضیات، به حاصلضرب هر عدد در خودش، مربع میگویند. با این وجود، منظور از عنوان «مربع» در واحد اندازهگیری مساحت، حاصلضرب دو عدد با واحد یکسان (مانند متر، اینچ و غیره) است.
روش های محاسبه مساحت چه هستند؟
سطح داخل مربع، معمولا با استفاده طول یک ضلع محاسبه میشود. البته در صورت دانستن مقدار اندازه قطر مربع یا مختصات دو راس مجاور، امکان اندازهگیری مساحت وجود خواهد داشت.
| اطلاعات مسئله | روش محاسبه مساحت مربع |
| طول یک ضلع | یک ضلع ضرب در خودش |
| طول قطر | قضیه فیثاغورس و رابطه کلی |
| مختصات دو راس مجاور | جمع برداری و رابطه کلی |
کاربرد مساحت مربع چیست؟
محیط اطراف ما از اجسام مختلف با شکلهای متفاوت تشکیل میشود. یکی از شکلهای پرکاربرد برای ساخت وسایل، مربع است. بسیاری از تابلوها، کاشیها، تختههای بازی، ظرفها، جعبهها، کلیدهای قطعات الکترونیکی و غیره با سطح مربعی شکل ساخته میشوند. آشنایی با نحوه محاسبه سطح اشغال شده توسط مربع میتواند در طراحی این وسایل و برخی از فعالیتهای روزمره به ما کمک کند.

حل مثال های کاربردی
در این بخش، چندین مثال متنوع و کاربردی را در زمینه تعیین مساحت مربع مورد بررسی قرار میدهیم.
مثال اول: تعیین مساحت قاب عکس
شخصی قصد دارد بر روی دیوار خود، یک قاب عکس مربعی شکل نصب کند. اگر طول یکی از ضلعهای این قاب عکس برابر 20 سانتیمتر باشد، سطح اشغال شده توسط آن بر روی دیوار چقدر خواهد بود؟

طبق فرمول مساحت مربع، داریم:
خودش یک ضلع = مساحت مربع
به این ترتیب:
خودش ضلع قاب = مساحت قاب عکس
طول ضلع قاب عکس برابر 20 سانتیمتر است. در نتیجه:
20 20 = مساحت قاب عکس
400 = مساحت قاب عکس
سطح اشغال شده توسط قاب عکس بر روی دیوار برابر 400 سانتیمتر مربع است.
مثال دوم: تعیین مساحت صفحه شطرنج
تصویر زیر، یک صفحه شطرنج ساخته شده بر روی یک میز مربعی شکل را نمایش میدهد. اگر طول ضلع هر یک از خانههای شطرنج برابر 3 سانتیمتر باشد، مساحت کل صفحه شطرنج چقدر خواهد بود؟

هر صفحه شطرنج، از 8 ردیف و 8 ستون تشکیل میشود. به این ترتیب، تعداد خانههای یک صفحه شطرنج برابر است با:
تعداد ستونها تعداد ردیفها = تعداد خانهها
8 8 = تعداد خانهها
64 = تعداد خانهها
هر صفحه شطرنج دارای 64 خانه است. تمام خانههای شطرنج دارای شکل مربعی هستند. مساحت یک خانه شطرنج از رابطه زیر به دست میآید:
خودش یک ضلع = مساحت مربع
3 3 = مساحت خانه شطرنج
9 = مساحت خانه شطرنج
به این ترتیب، مساحت یکی از خانههای شطرنج برابر 9 سانتیمتر مربع خواهد بود. در نتیجه، مساحت کل صفحه شطرنج از رابطه زیر به دست میآید:
تعداد خانهها مساحت یک خانه = مساحت صفحه شطرنج
64 9 = مساحت صفحه شطرنج
576 = مساحت صفحه شطرنج
مساحت صفحه شطرنج مورد سوال برابر 576 سانتیمتر مربع است.
مثال سوم: مساحت قسمت سطح خالی میز
مثال قبلی را در نظر بگیرید. اگر طول یکی از ضلعهای سطح میز مربعی شکل برابر 36 سانتیمتر باشد، مساحت سطح خالی میز چقدر خواهد بود؟
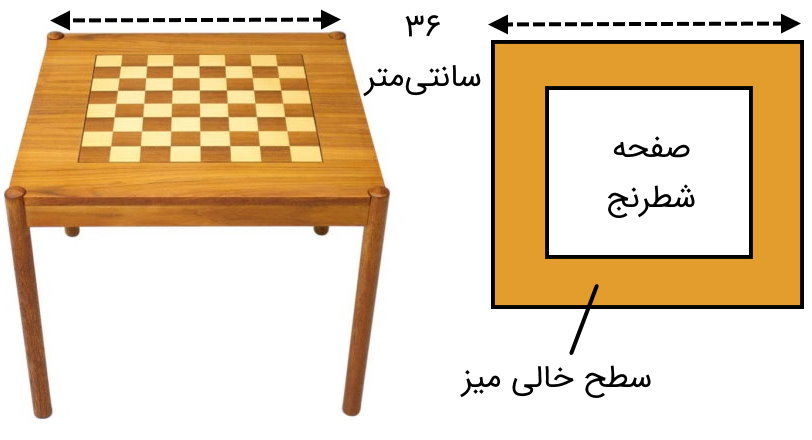
به منظور تعیین سطح خالی میز (مساحت قسمت رنگی مربع در تصویر بالا)، باید مساحت صفحه شطرنج را از مساحت کل میز کم کنیم. بر این اساس، داریم:
مساحت صفحه شطرنج - مساحت کل سطح میز = مساحت خالی میز
با توجه به مثال قبلی، مساحت صفحه شطرنج برابر 576 سانتیمتر مربع است. مساحت کل سطح میز از رابطه زیر به دست میآید:
خودش طول یک ضلع میز = مساحت کل میز
36 36 = مساحت کل میز
1296 = مساحت کل میز
مساحت کل میز برابر 1296 سانتیمتر مربع است. در نتیجه:
مساحت صفحه شطرنج - مساحت کل سطح میز = مساحت خالی میز
576 - 1296 = مساحت خالی میز
720 = مساحت خالی میز
مساحت فضای خالی برابر با 720 سانتیمتر مربع است.
مثال چهارم: مقایسه مساحت مستطیل و مربع
تصویر زیر، یک مربع و یک مستطیل را نمایش میدهد. با توجه به اطلاعات تصویر، مساحت کدام یک از این شکلها بیشتر است.
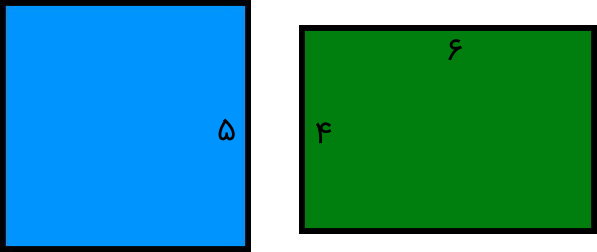
محاسبه مساحت مربع به صورت زیر انجام میشود:
خودش یک ضلع = مساحت مربع
5 5 = مساحت
25 = مساحت
مساحت مربع برابر 25 است. مساحت مستطیل مطابق با رابطه زیر به دست میآید:
عرض طول = مساحت مستطیل
4 6 = مساحت مستطیل
24 = مساحت مستطیل
به این ترتیب، در این مثال، مساحت مربع بیشتر از مساحت مستطیل است.
مثال پنجم: تعیین مساحت با محیط
مساحت مربعی با محیط 20 سانتیمتر را محاسبه کنید.
محیط مربع، مجموع اندازه ضلعهای آن است. از آنجایی که تمام ضلعهای مربع با یکدیگر برابر هستند، فرمول محیط مربع به صورت حاصلضرب یک ضلع در 4 نوشته میشود::
طول یک ضلع 4 = محیط مربع
مقدار محیط از صورت سوال را درون رابطه بالا قرار میدهیم:
طول یک ضلع 4 = 20
طول یک ضلع = 4 ÷ 20
طول یک ضلع = 5
5 = a
طول یک ضلع مربع برابر 5 سانتیمتر است. با مشخص شدن طول، میتوان مساحت مربع را نیز به صورت محاسبه کرد:
خودش یک ضلع = مساحت مربع
5 5 = مساحت
25 = مساحت
در نتیجه، مساحت مربعی با محیط 20 سانتیمتر برابر 25 سانتیمتر مربع است.
مثال ششم: تعیین طول ضلع مربع
طول ضلع مربعی با مساحت 81 متر مربع چقدر است؟
مطابق با رابطه مساحت مربع داریم:
رابطه بالا را میتوان به صورت زیر بازنویسی کرد:
به عبارت دیگر، طول ضلع مربع برابر جذر مساحت آن است. بنابراین:
در نتیجه، طول ضلع مربع برابر 9 سانتیمتر است.
مثال هفتم: تعیین مساحت مجموعه مربعها
تصویر زیر، سه مربع روی هم را نمایش میدهد. اگر طول ضلع مربع 1، دو برابر طول ضلع مربع 2 و طول ضلع مربع 2، دو برابر طول ضلع مربع 3 باشد، مجموع مساحت هر سه مربع چقدر خواهد بود؟
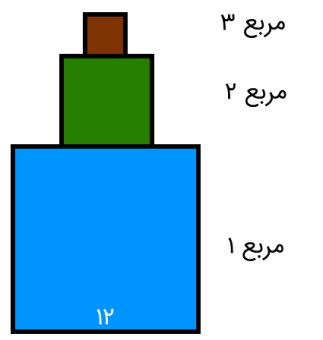
مجموع مساحت مربعها برابر است با:
مساحت مربع 3 + مساحت مربع 2 + مساحت مربع 1 =مساحت کل
به دلیل مشخص بودن طول ضلع مربع 1، ابتدا مساحت این مربع را محاسبه میکنیم:
12 12 = مساحت 1
144 = مساحت 1
طول ضلع مربع 1، دو برابر طول ضلع مربع 2 است. بنابراین:
طول ضلع مربع 2 2 = طول ضلع مربع 1
طول ضلع مربع 2 2 = 12
طول ضلع مربع 2 = 6
مساحت مربع 2 از رابطه زیر به دست میآید:
خودش طول ضلع مربع 2 = مساحت 2
6 6 = مساحت 2
36 = مساحت 2
طول ضلع مربع 3 نیز نصف طول ضلع مربع دو است. به عبارت دیگر:
3 = طول ضلع مربع 3
مساحت مربع 3 نیز مانند دیگر مربعها محاسبه میشود:
خودش طول ضلع مربع 3 = مساحت 3
3 3 = مساحت 3
9 = مساحت 3
اکنون میتوانیم مساحت کل را محاسبه کنیم:
مساحت 3 + مساحت 2 + مساحت 1 =مساحت کل
9 + 36 + 144 =مساحت کل
189 =مساحت کل
مساحت مجموع سه مربع برابر 189 است.
مساحت مربع با قطر
یکی دیگر از روشهای محاسبه مساحت مربع، تعیین قطر آن و استفاده از قضیه فیثاغورس است.
در این روش، مساحت مربع با قطر از رابطه زیر به دست میآید:
2 ÷ خودش قطر = مساحت مربع
به عبارت دیگر:
2 ÷ ۲(قطر) = مساحت مربع
فرمول مساحت مربع با قطر
فرمول ریاضی مساحت مربع با قطر به صورت زیر نوشته میشود:
- A: مساحت
- d: قطر
اثبات فرمول مساحت
اگر قطر مربع را رسم کنیم، دو مثلث قائم الزاویه به وجود میآید.
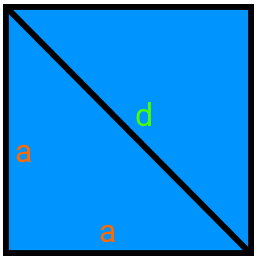
مطابق با قضیه فیثاغورس داریم:
- a: یکی از ساقهای مثلث قائم الزاویه
- b: ساق دیگر مثلث قائم الزاویه
- c: وتر مثلث قائم الزاویه
در تصویر بالا، هر دو ساق برابر ضلع مربع با طول a و وتر برابر قطر مربع با طول d است. به این ترتیب:
a2، همان مساحت مربع است. در نتیجه:
مثال اول: تعیین سطح مربع از روی قطر آن
مساحت مربعی به قطر 12 سانتیمتر، چقدر است؟
مطابق با فرمول مساحت مربع با قطر، داریم:
مساحت مربعی با قطر 12 سانتیمتر برابر 72 سانتیمتر مربع است.
مثال دوم: تعیین مساحت مربع محاط در دایره
تصویر زیر، یک مربع محاط در دایره را نمایش میدهد. اگر شعاع دایره برابر 3.5 سانتیمتر باشد، مساحت مربع چقدر است؟

مربع محاط دایره، مربعی است که مانند تصویر بالا، تمام راسهای آن بر روی محیط دایره قرار میگیرند. در این حالت، قطر مربع برابر با قطر دایره است. مطابق با صورت سوال، شعاع دایره برابر 3.5 سانتیمتر است. به این ترتیب:
2 شعاع دایره = قطر دایره
2 3.5 = قطر دایره
7 = قطر دایره
در نتیجه، قطر مربع محاط در دایره برابر 7 سانتیمتر است. بر اساس فرمول مساحت مربع با قطر، داریم:
مساحت مربع محاط در دایره برابر 24.5 سانتیمتر مربع است.
نسبت مساحت مربعهای متشابه
نسبت مساحتهای دو مربع متشابه برابر نسبت ضلعهای آنها به توان دو است.
فرمول ریاضی نسبت مساحت دو مربع متشابه به صورت زیر نوشته میشود:
- A1: سطح مربع اول
- A2: سطح مربع دوم
- a1: ضلع مربع اول
- a2:ضلع مربع دوم
در رابطه بالا، به جای طول ضلعها از طول قطرها نیز میتواند استفاده کرد. توجه داشته باشید که بر اساس قواعد تشابه در اشکال هندسی، تمام مربعها متشابه هستند.
مثال: تعیین ضلع مربع بر اساس نسبت مساحتها
تصویر زیر، دو مربع متشابه را نمایش میدهد. اگر نسبت مساحت مربع بزرگ به کوچک برابر 4 باشد، طول ضلع مربع بزرگ چقدر خواهد بود؟
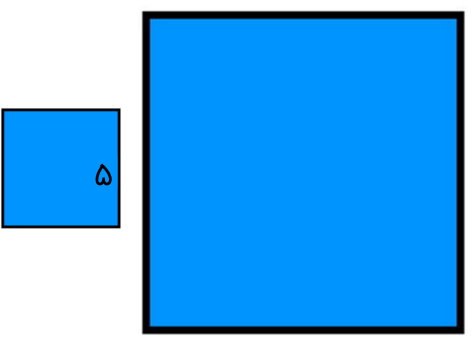
بر اساس فرمول نسبت مساحت دو مربع متشابه، داریم:
پارامترهای رابطه بالا را به صورت زیر در نظر میگیریم:
- A1: سطح مربع بزرگ
- A2: سطح مربع کوچک
- a1: ضلع مربع بزرگ
- a2:ضلع مربع کوچک و برابر 5
مقادیر موجود را درون رابطه قرار میدهیم:
ضلع مربع بزرگتر برابر 10 است.
آزمون مساحت مربع
۱. در تعریف هندسی، چه تفاوت کلیدی بین مربع و مستطیل از نظر ویژگی اضلاع و زوایا وجود دارد؟
در مستطیل فقط اضلاع مجاور برابراند، اما در مربع هیچ ضلعی برابر نیست.
در مربع قطر برابر ندارد، اما در مستطیل این ویژگی وجود دارد.
در مربع همه اضلاع برابرند، اما در مستطیل فقط اضلاع روبرو برابرند.
در مستطیل همه زوایا قائمه نیست، اما در مربع همه زوایا قائمهاند.
ویژگی مهم مربع این است که هر چهار ضلع آن هماندازه هستند، در حالی که در مستطیل فقط اضلاع روبهروی هم با هم برابرند. همچنین هر دو شکل دارای زوایای قائمهاند، پس تفاوت آنها از نظر طول اضلاع است.
۲. اگر طول ضلع مربعی ۸ سانتیمتر باشد، مساحت آن با چه فرمولی و چه نمادهایی محاسبه میشود؟
A = d × d با A مساحت و d قطر مربع
A = a × a با A مساحت و a طول ضلع
A = (d^2) / 4 با A مساحت و d قطر مربع
A = 2 × a با A مساحت و a طول ضلع
فرمول درست برای محاسبه مساحت مربع، ضرب طول ضلع در خودش است که به صورت A = a × a نوشته میشود؛ در این فرمول، A نماد مساحت (Area) و a نماد طول ضلع مربع است.
۳. برای اندازهگیری مساحت یک صفحه دوبعدی، کدام نوع واحد مناسبتر است و چرا استفاده از واحد طولی مناسب نمیباشد؟
میلیمتر (mm) انتخاب خوبی است، چون برای اندازه سطح کاربرد دارد.
بکارگیری متر (m) بهتر است، چون ظاهر ساده دارد.
استفاده از سانتیمتر (cm) کافی است، چون طول ضلع را مشخص میکند.
استفاده از سانتیمتر مربع (cm²) مناسب است، چون تمام سطح را پوشش میدهد.
برای سنجش مساحت یک سطح دوبعدی لازم است از واحدهایی مانند «سانتیمتر مربع (cm²)» استفاده شود، زیرا این واحدها مساحت کل ناحیه را بیان میکنند. اگر واحد خطی مانند «سانتیمتر» یا «متر» بهکار رود، فقط یک بُعد اندازهگیری میشود و تمام فضای داخلی سطح پوشش داده نمیشود. بسته به ابعاد، میتوان از میلیمتر مربع یا متر مربع نیز استفاده کرد، اما بهطور کلی واحدهای طولی مانند «سانتیمتر» یا «متر» مناسب سنجش مساحت نیستند، زیرا فقط اندازه یک ضلع را نمایش میدهند نه وسعت کل سطح.
۴. اگر فقط طول قطر یک مربع داده شده باشد، بهترین روش برای محاسبه مساحت آن با استفاده از فرمول و نمادهای ریاضی چیست؟
ضرب قطر در چهار
جمع کردن قطر و ضلع و ضرب در دو
محاسبه قطر به توان دو و تقسیم بر دو
ضرب قطر در ضلع و تقسیم بر دو
برای محاسبه مساحت مربع با استفاده از قطر، از فرمول مساحت برابر است با قطر به توان دو تقسیم بر دو استفاده میشود، یعنی (d^2)/2. استفاده از عبارت «محاسبه قطر به توان دو و تقسیم بر دو» دقیقا مطابق این روش است. سایر روشها مانند «ضرب قطر در ضلع و تقسیم بر دو» یا «جمع کردن قطر و ضلع و ضرب در دو» هیچکدام فرمول صحیح مربوط به مساحت مربع وقتی فقط قطر داده شده را نشان نمیدهند. همچنین «ضرب قطر در چهار» مربوط به محیط نیست و برای مساحت کاربرد ندارد.
۵. در صورت تشابه دو مربع، ارتباط بین نسبت ضلعها و نسبت مساحتهای آنها چیست و دلیل این رابطه کدام است؟
نسبت مساحتها نصف نسبت ضلعهاست، چون یکی از اضلاع فاکتور گرفته میشود.
نسبت مساحتها برابر با مربع نسبت ضلعهاست، چون مساحت مربع از ضرب دو ضلع برابر محاسبه میشود.
نسبت مساحتها مساوی با نسبت ضلعهاست، چون هر مربع فقط یک بعد دارد.
نسبت مساحتها مستقل از نسبت ضلعهاست و تنها به قطر مربوط است.
رابطه بین نسبت مساحتهای دو مربع متشابه به این صورت است که نسبت مساحتها برابر با مربع نسبت ضلعها خواهد بود، چون مساحت هر مربع از ضرب ضلع در خودش (a × a) یا به صورت a^2 به دست میآید؛ بنابراین اگر نسبت ضلع دو مربع برابر با x باشد، آنگاه نسبت مساحتها برابر با x^2 خواهد بود. پاسخهایی مانند «مساوی بودن نسبت مساحتها با نسبت ضلعها» یا «نصف بودن نسبت مساحتها» نادرست است، چون مساحت، تابعی درجه دوم از ضلع است. همچنین، مساحت صرفا به قطر وابسته نیست و رابطه دقیق با نسبت اضلاع دارد.
۶. کدام مورد نمونهای کاربردی از اهمیت دانستن مساحت مربع در زندگی یا صنعت است؟
محاسبه وزن آسانسور مورد نیاز یک ساختمان
برآورد تعداد کاشیهای لازم برای پوشاندن زمین
انتخاب رنگ دیوار برای زیباسازی اتاق
تعیین ضخامت سیمکشی ساختمان
دانستن مساحت مربع برای «برآورد تعداد کاشیهای لازم برای پوشاندن زمین» اهمیت عملی دارد، زیرا مساحت تعیینکننده تعداد واحدهای سطح برای پوششدهی کامل است. سایر موارد مثل «تعیین ضخامت سیمکشی ساختمان» یا «انتخاب رنگ دیوار برای زیباسازی اتاق» بیشتر با حجم یا ظاهر مرتبط هستند و نقش مستقیمی برای مساحت مربع ندارند. همینطور «محاسبه وزن آسانسور» ارتباطی با سطح مربع نخواهد داشت.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مربع — تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مربع چیست ؟ — تعریف و مفاهیم به زبان ساده (+ فیلم آموزش رایگان)
- قطر مربع چیست و چگونه بدست می آید ؟ — به زبان ساده + حل تمرین و مثال
- چگونه محیط مربع را حساب کنیم؟ + فیلم آموزشی و حل تمرین
- مساحت مربع چگونه بدست می آید؟ + فیلم آموزشی و حل تمرین و مثال(همین مطلب)
- طول ضلع مربع به محیط آن چیست؟ + حل تمرین و مثال
- فرمول محیط مربع چیست ؟ — به زبان ساده + حل تمرین و مثال
- فرمول مساحت مربع چیست ؟ — به زبان ساده + حل تمرین و مثال
- محیط مربع به صورت جبری — فرمول های ریاضی + حل تمرین و مثال
- مساحت مربع به صورت جبری — فرمول های ریاضی + حل تمرین و مثال
- مساحت مربع داخل دایره چگونه بدست می آید ؟ — به زبان ساده + تمرین و مثال
- مساحت مربع با قطر چگونه بدست می آید ؟ – به زبان ساده + حل تمرین و مثال













خیلی عالی بود متشکرم
من کمی مبتدی هستم لطفا اگه وقت کردید پاسخ این سوال رو بدید استاد ممنونم :
معادله تابعی که مساحت مربع را به قطر آن وابسته کند
و
معادله تابعی که مساحت مربع را به ظلع آن وابسته کند
سلام.
اگر فرض کنیم مساحت مربع A باشد و قطر آن d، آنگاه تابع مساحت بهصورت A(d)=2d2 خواهد بود. همجنین، با فرض اینکه ضلع مربع a است، تابع مساحت آن A(a)=a2 است.
سالم و موفق باشید.