تونل زنی کوانتومی چیست؟ – به زبان ساده

درک فیزیک کوانتوم و برخی مفاهیم آن بسیار سخت است. این شاخه از فیزیک به جهان میکروسکوپی و رفتار آن می‌پردازد. جهان در این مقیاس نسبت به جهانی که می‌شناسیم، بسیار متفاوت است. هنگامی که به دنیای اتم‌ها سفر می‌کنیم، قوانین فیزیک کلاسیک کاربردی نخواهند داشت. به عنوان مثال، یک ذره در دنیای ماکروسکوپی، یک ذره و موج، یک موج است. اما بر طبق قوانین کوانتومی، الکترون‌ها می‌توانند همانند ذره یا موج رفتار کنند. حتی اجسام ممکن است در یک زمان در حالت‌های متفاوتی قرار داشته باشند. از این ویژگی برای ساخت کامپیوترهای کوانتومی استفاده شده است. یکی از عجیب‌ترین موضوع‌های مطرح شده در فیزیک کوانتوم، تونل زنی کوانتومی است.

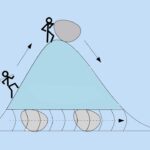
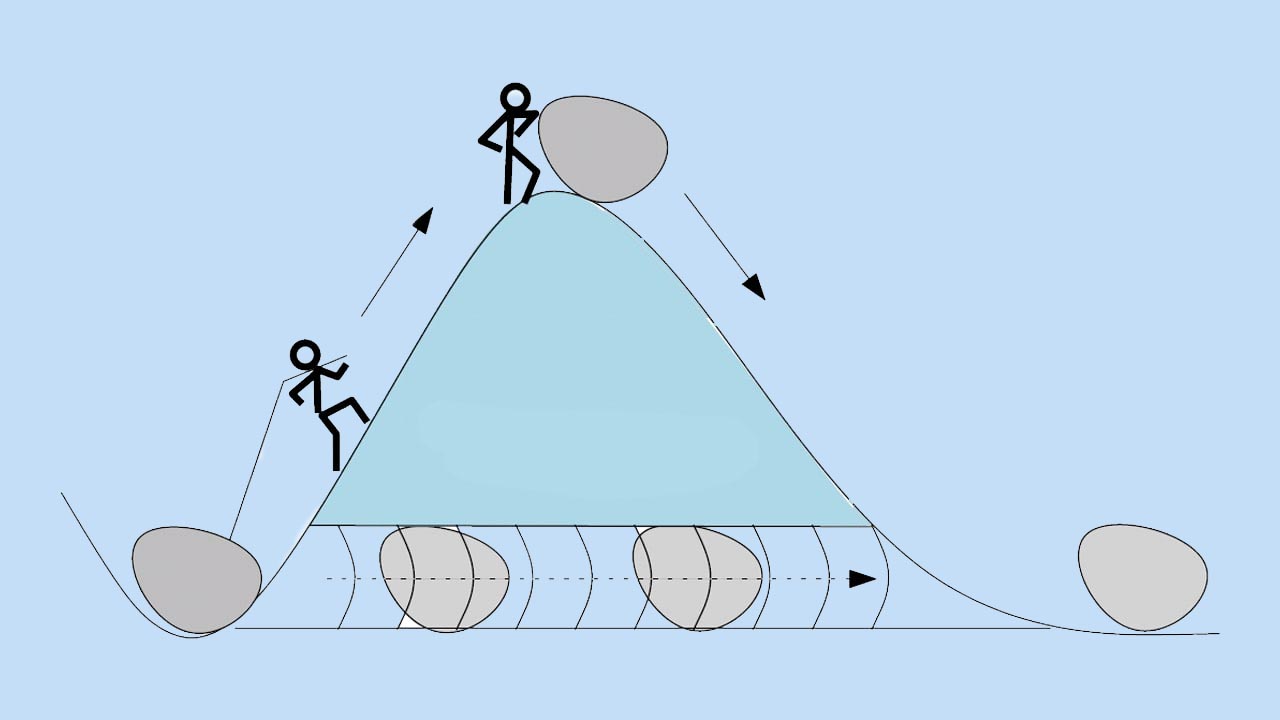
فرض کنید ذره‌ای مانند الکترون یا پروتون را در فضا و در یک طرف سد انرژی پتانسیل قرار می‌دهید. از آنجا که می‌دانید انرژی ذره به اندازه‌ای نیست که از سد پتانسیل بالا و به طرف دیگر سد انرژی برود، آن را برای مدت زمان مشخصی به حال خود رها می‌کنید. پس از بازگشت، اثری از ذره در مکان اولیه نخواهید یافت، بلکه آن را سمت دیگر سد پیدا می‌کنید. ذره موردنظر با حفر تونل به سمت دیگر سد انرژی رفته است. این پدیده بسیار عجیب و در تناقض با قوانین فیزیکی به نظر می‌رسد. در این مطلب، در مورد پدیده تونل زنی کوانتومی، کاربردهای این پدیده و هر آنچه در مورد آن باید بدانید، به زبان ساده صحبت خواهیم کرد. در پایان، کمی در مورد ریاضیات حاکم بر پدیده تونل زنی نیز توضیح می‌دهیم.

تونل زنی کوانتومی چیست ؟

فرض کنید در یک سمت تپه‌ای با ارتفاع مشخص ایستاده‌اید. برای آن‌که به سمت دیگر تپه بروید، هیچ راهی جز بالا رفتن از آن نخواهید داشت. البته راه دیگری نیز وجود دارد. با استفاده از بیل و کلنگ تونلی در تپه حفر کنید و به سمت دیگر بروید. اکنون این مثال ساده را در دنیای فیزیک کوانتوم شبیه‌سازی می‌کنیم. تپه در فیزیک کوانتوم، همان سد انرژی است. برای بالا رفتن از تپه باید انرژی مصرف کنید. اگر خسته یا گرسنه باشید، انرژی کافی برای بالا رفتن از تپه را نخواهید داشت.

نقش شما در فیزیک کوانتوم توسط ذره‌ای مانند الکترون یا پروتون ایفا می‌شود. ذره در یک سمت سد انرژی قرار گرفته است. اگر انرژی ذره به اندازه کافی زیاد باشد، به راحتی از سد انرژی عبور خواهد کرد. اما اگر انرژی آن به اندازه‌ای نباشد که از سد عبور کند، چه اتفاقی رخ می‌دهد؟ برای پاسخ به این پرسش، باید نگاه دوگانه‌ای به ذره‌ای مانند الکترون داشته باشیم. در اینجا، رفتار دوگانه موج-ذره مطرح می‌شود. بر طبق رفتار دوگانه موج-ذره، الکترون نه‌تنها به شکل ذره، بلکه به شکل موج نیز رفتار می‌کند. بنابراین، رفتار موجی الکترون بیان می‌کند که این ذره با احتمال‌های مختلف، در هر جایی از فضا ممکن است قرار داشته باشد. موج نسبت داده شده به الکترون به وجود سد انرژی هیچ اهمیتی نمی‌دهد، گویی آن را اصلا نمی‌بیند.

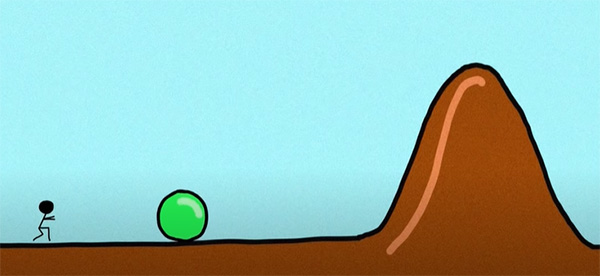
اکنون پرسیدن این سوال منطقی به نظر می‌رسد، آیا قسمتی از موج در سمت دیگر تپه، ظاهر خواهد شد؟ اگر پاسخِ این پرسش، بله باشد، الکترون یا هر ذره کوانتومی دیگر، با احتمال مشخصی در سمت دیگر سد ظاهر می‌شود. به این پدیده، تونل زنی کوانتومی گفته می‌شود. این پدیده در فیزیک کلاسیک غیرممکن است. به تصویر زیر دقت کنید. برای آن‌که سنگ به سمت دیگر تپه برود، باید مقدار انرژی جنبشی که به آن می‌دهیم، از انرژی پتانسیل تپه بیشتر باشد. در غیر این صورت نمی‌تواند به سمت دیگر تپه برود. در فیزیک کلاسیک، سنگ یا این سمت تپه قرار دارد یا سمت دیگر. اما این حالت در دنیای کوانتوم و برای ذره‌ای مانند الکترون، متفاوت است.

یکی از مهم‌ترین تفاوت‌های فیزیک کلاسیک و فیزیک کوانتوم آن است که احتمالات بر فیزیک کوانتوم، حاکم است. به طور دقیق نمی‌توانیم مکان الکترون را در فضا مشخص کنیم، بلکه قرار گرفتن الکترون در مکان x را با احتمال مشخصی بیان می‌کنیم. دلیل این موضوع به اصل عدم قطعیت هایزنبرگ برمی‌گردد. در ادامه، در مورد این اصل با جزییات بیشتری صحبت خواهیم کرد. رفتار الکترون در مقیاس کوانتومی را با جزییات بیشتری توضیح می‌دهیم. الکترونی را در نظر بگیرید که تنها می‌تواند روی محور x، به سمت چپ یا راست، حرکت کند. حرکت الکترون به سمت راست را مثبت و حرکت آن به سمت چپ را منفی در نظر می‌گیریم. در این حالت، گرچه الکترون به حرکت در یک‌بعد محدود شده است، آن را به عنوان الکترون آزاد در نظر می‌گیریم. زیرا هیچ نیروی خارجی بر آن وارد نمی‌شود.

به بیان دیگر، هیچ عامل خارجی بر حرکت الکترون تاثیر نمی‌گذارد. اکنون سد انرژی را به عنوان عامل خارجی، وارد این سیستم می‌کنیم. سوالی که ممکن است مطرح شود آن است که سد انرژی چگونه ایجاد می‌شود. یک راه آسان برای انجام این کار، وارد کردن الکترونی ساکن به سیستم متشکل از الکترون آزاد است. وجود این الکترون، سدی در برابر حرکت آزادانه الکترون اول خواهد بود.

ابتدا به این سوال پاسخ می‌دهیم که چگونه وجود الکترون دوم، حرکت الکترون اول را مختل خواهد کرد. از آنجا که بار الکتریکی الکترون‌ها یکسان و منفی است، یکدیگر را با نیروی الکترواستاتیکی دفع می‌کنند. فرض کنید الکترون اول در مکان $$x_1$$ و الکترون دوم در مکان $$x_2$$ قرار دارند. الکترون اول را به سمت الکترون دوم حرکت می‌دهیم. این الکترون تا جایی به الکترون دوم نزدیک می‌شود که نیروی دافعه الکترواستاتیکی را احساس کند. در اینجا، دو حالت اتفاق می‌افتد:

1. اگر نیروی اولیه وارد شده به الکترون اول برای نزدیک کردن آن به الکترون دوم کافی نباشد، این الکترون پس از نزدیک شدن به الکترون دوم و وارد شدن نیروی دافعه الکترواستاتیکی به آن، به عقب برمی‌گردد.
2. اگر نیروی اولیه وارد شده به الکترون اول برای نزدیک کردن آن به الکترون دوم بسیار زیاد باشد، انرژی جنبشی این الکترون به اندازه‌ای است که بر نیروی دافعه الکترواستاتیکی غلبه و از آن عبور کند.

حالت بالا در تصویر زیر نشان داده شده است. الکترون اول روی محور افقی x حرکت می‌کند. نیروی دافعه بین دو الکترون به صورت تپه‌ای در این محور نشان داده شده است و سد پتانسیل نام دارد. همچنین، مقدار انرژی اولیه داده شده به الکترون اول را نیز می‌توان در این نمودار نشان داد. اگر انرژی اولیه داده شده به الکترون به اندازه کافی بزرگ نباشد، از سد پتانسیل الکترون دوم نخواهد گذشت.

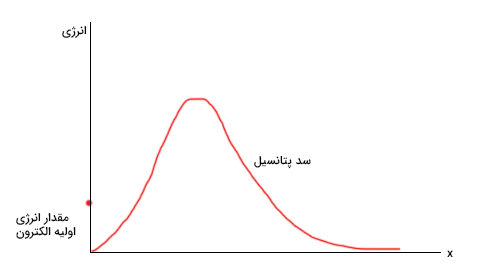
سد پتانسیل ایجاد شده توسط الکترون ممکن است پیچیده باشد و رسم شکل آن کار آسانی نخواهد بود. بنابراین، سد پتانسیل را به شکل بسیار ساده‌تری در نظر می‌گیریم. این نکته را به یاد داشته باشید که شکل سد پتانسیل هرچه باشد، فیزیک حاکم بر تونل زنی کوانتومی تغییری نخواهد کرد. همان‌طور که در تصویر زیر نشان داده شده است، پتانسیل در تمام فضا، به جز فاصله $$x=0$$ و $$x= a$$، برابر صفر است. در این فاصله، پتانسیل برابر $$u$$ خواهد بود. سد پتانسیل در این حالت شبیه پله است. همچنین، این سد پتانسیل فضا را به سه قسمت تقسیم کرده است:

1. xهای کوچک‌تر از صفر
2. xهای بین صفر و a
3. xهای بزرگ‌تر از a

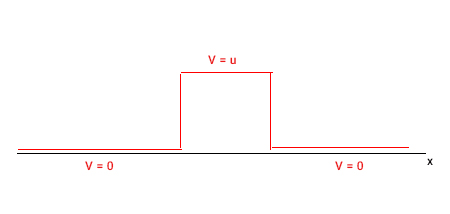
اکنون الکترونی را در سمت چپِ سد پتانسیل قرار می‌دهیم. بر طبق فیزیک کلاسیک، الکترون، تنها هنگامی می‌تواند از این سد عبور کند که انرژی اولیه آن بیشتر از ارتفاع سد پتانسیل باشد. اما فیزیک کوانتوم به این سادگی نخواهد بود. گفتیم تمام اطلاعات ذره‌ کوانتومی مانند سرعت یا مکان آن در تابع موج نسبت داده شده به آن نهفته است. همچنین، تابع موج به صورت مستقیم متناسب با تابع توزیع احتمال ذره کوانتومی خواهد بود. در فیزیک کلاسیک با اطمینان می‌گوییم الکترون در این زمان در مکان a و چند لحظه بعد در مکان b قرار دارد، اما در فیزیک کوانتوم با اطمینان نمی‌توانیم در مورد مکان الکترون صحبت کنیم. هر آنچه در مورد مکان الکترون می‌گوییم برحسب احتمالات است.

سوالی که ممکن است مطرح شود آن است که تابع موج الکترون در هر ناحیه از فضا (سه ناحیه گفته شده در مطالب بالا)‌ به چه شکل خواهد بود. برای پاسخ به این پرسش، باید معادله شرودینگر برای این الکترون را حل کنیم. در ادامه، معادله را با جزییات ریاضی کامل حل خواهیم کرد. معادله شرودینگر را برای دو حالت حل می‌شود:

1. انرژی الکترون از سد پتانسیل بیشتر باشد.
2. انرژی الکترون از سد پتانسیل کمتر باشد.

در حالت اول، نکته جدیدی وجود ندارد و الکترون از سد پتانسیل عبور خواهد کرد. حالت دوم، برای ما جالب است و تونل زنی کوانتومی برای این حالت رخ می‌دهد. بر طبق فیزیک کلاسیک، اگر انرژی الکترون از ارتفاع سد پتانسیل کمتر باشد، احتمال یافتن الکترون در سمت دیگر سد، برابر صفر است. در فیزیک کوانتوم، تابع موج الکترون را در نظر می‌گیریم. به بیان دیگر، الکترون به صورت موج در نظر گرفته می‌شود. اگر معادله شرودینگر را برای این حالت حل کنیم، متوجه خواهیم شد که تابع موج الکترون در سمت دیگر سد پتانسیل، غیرصفر است. بنابراین، الکترون با احتمال مشخصی در آنجا یافت می‌شود. به عبارت دیگر، تابع موج الکترون به داخل سد نفوذ و به سمت دیگر سد می‌رود.

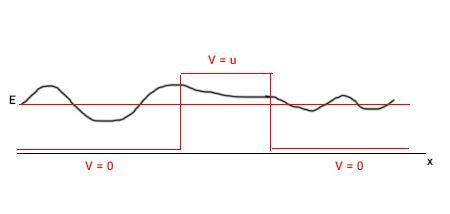
بنابراین، تونل زنی کوانتومی پدیده‌ای کاملا کوانتومی است و در فیزیک کلاسیک جایگاهی ندارد. به شکل تابع موج داخل سد پتانسیل دقت کنید. این تابع، داخل سد به صورت نمایی افت کرده است. این بدان معنا است که احتمال یافتن الکترون داخل سد و پس از آن، به صورت نمایی کاهش می‌یابد. هرچه طول سد بیشتر باشد، احتمال یافتن الکترون در سمت دیگر آن کمتر است. در مقابل، هرچه طول سد کمتر باشد، احتمال یافتن الکترون در سمت دیگر آن بیشتر خواهد بود.

آیا تونل زنی کوانتومی سریع تر از سرعت نور است ؟

به احتمال زیاد اگر به فیلم‌های علمی-تخیلی علاقه‌مند باشید، در قسمتی از فیلم می‌بینید که قهرمان داستان در یک زمان در همه‌جا حضور دارد. بدون شک، سازنده این فیلم، به فیزیک کوانتوم علاقه‌مند بوده است. فیزیک کوانتوم یکی از عجیب‌ترین نظریه‌های مطرح شده در فیزیک است. یکی از اصل‌های پایه کوانتوم می‌گوید که ویژگی‌های جسمی مشخص، مانند سرعت یا مکان‌ آن، به صورت بنیادی نامشخص هستند. به عنوان مثال، نمی‌توان گفت الکترون به طور قطع در مکان مشخصی قرار گرفته است یا با این سرعت حرکت می‌کند. به جای آن، می‌گوییم الکترون با احتمالی مشخصی در این حالت قرار دارد. هر حالت معینی، احتمال مشخصی دارد.

تا هنگامی که ذره کوانتومی با چیزی برهم‌کنش نکند، تمام حالت‌های ممکن به یک اندازه، واقعی هستند. اما باید توجه داشته باشیم که احتمال آن‌ها ممکن است یکسان نباشد. در واقع، به جای احتمال تک، توزیع احتمال داریم. این توزیع احتمال و چگونگی تغییر آن با زمان، در تابعی به نام تابع احتمال، قرار گرفته است. گاهی به کاهش احتمالِ درهم در فضا و تبدیل آن به ویژگی قابل‌اندازه‌گیری مشخص، فروپاشی تابع موج گفته می‌شود. عدم قطعیت در مکان ذره کوانتومی، سبب نتیجه بسیار عجیبی در فیزیک کوانتوم به نام رفتار دوگانه موج-ذره شد. دوبروی، نخستین کسی بود که به این نتیجه عجیب رسید.

این فیزیک‌دان، طول موجی برای ذره کوانتومی به نام طول موج دوبروی تعریف کرد. اگر مقدار این طول موج، بزرگ باشد، عدم قطعیت در تعیین مکان ذره بسیار زیاد خواهد بود. در مقابل، اگر اندازه آن کوچک باشد، عدم قطعیت در تعیین مکان ذره کم است و مکان آن را می‌توان با دقت نسبتا خوبی تعیین کرد. این مورد به خوبی برای ذرات زیراتمی و به طور تقریب برای هر چیزی صدق می‌کند. به این مثال توجه کنید. فرض کنید به هنگام خواندن این مطلب روی صندلی در اتاق خود نشسته‌اید. احتمال کوچکی وجود دارد که در مترو، تاکسی یا اتوبوس و حتی احتمال بسیار اندکی وجود دارد که در کره ماه باشید. اگر کسی شما را مشاهده کند، تابع احتمال مربوط به شما از بین خواهد رفت.

طول موج دوبروی جسم به تکانه جسم بستگی دارد. می‌دانیم تکانه برابر حاصل‌ضرب جرم ذره در سرعت حرکت آن است. هر چه تکانه ذره‌ای بیشتر باشد، طول موج دوبروی آن کوچک‌تر خواهد بود. بیان ریاضی این طول موج برابر است با:

$$\lambda = \frac { h} {p}$$

دانشمندان، ذرات کوچکی را با استفاده از انرژی گرمایی به حرکت درآوردند و طول موج دوبروی آن‌ها را اندازه گرفتند. مقدار به‌دست آمده برای این طول موج، چندین مرتبه از طول پلانک کوچک‌تر بود. شما می‌توانید هر جایی در جهان باشید، ولی با احتمال‌های مختلف.

اجازه دهید به مقیاس کوانتومی برویم و ذره‌ای مانند آلفا را در نظر بگیریم. این ذره از دو پروتون و دو نوترون تشکیل شده است. ذره آلفا به صورت تکی همان هسته هلیوم است. این ذره را به عنوان قسمتی از هسته‌های اتمی سنگین‌تر نیز می‌توان در نظر گرفت. در این حالت، ذره آلفا توسط نیروی هسته‌ای قوی، پیوند محکمی با هسته دارد. ذره آلفا را می‌توان به صورت توپی در نظر گرفت که داخل چاه پتانسیل عمیقی به دام افتاده است. توپ، داخل چاه پتانسیل به اطراف حرکت می‌کند، اما به راحتی نمی‌تواند از آن خارج شود. تنها در صورتی که انرژی جنبشی بزرگی به توپ داده شود، از چاه پتانسیل خارج می‌شود.

ذره کوانتومی هیچ شباهتی به توپ ندارد. همان‌طور که گفته شد موقعیت مکانی آن‌ها را نمی‌توان به طور دقیق مشخص کرد. بسته موجی به ذره آلفا نسبت داده می‌شود. این بسته گستره‌ای از مکان‌های محتمل را توصیف می‌کند. مقدار تابع احتمال، به طور ناگهانی در سد پتانسیل، صفر نمی‌شود. به جای آن، مقدار این تابع به صورت نمایی و با شدت زیادی افت می‌کند. گرچه، مقدار آن هیچ‌گاه به طور کامل صفر نخواهد شد، اما به سمت صفر میل می‌کند. بنابراین، ذره آلفا با احتمال بسیار کوچکی، بیرون هسته اتم نیز وجود دارد. در نتیجه، تونل زنی کوانتومی داخل هسته اتم‌ها نیز مشاهده می‌شود. هنگامی که ذره آلفا از هسته خارج می‌شود یا به اصطلاح فرار می‌کند، پرتوزایی تشعشعی رخ می‌دهد. تونل زنی کوانتومی در این فرایند نقش مهمی را ایفا می‌کند.

حالت دیگری از تونل زنی کوانتومی را نیز می‌توان در نظر گرفت. پروتون‌ها، نوترون‌ها، الکترون‌ها و ذرات آلفا می‌توانند به داخل هسته از راه همجوشی هسته‌ای، تونل بزنند. در واقع، اگر پدیده‌ای به نام تونل زنی کوانتومی وجود نداشت، ستاره‌ها نمی‌توانستند هیدروژن را با استفاده از همجوشی به هسته‌های سنگین‌تر تبدیل کنند. حتی صنعت الکترونیک، مانند ترانزیستورها، به تونل زنی کوانتومی وابسته هستند. سوالی که ممکن است مطرح شود آن است که ذره آلفا با چه سرعتی از سد پتانسیل عبور می‌کند. تا جایی که می‌دانیم این عبور به صورت آنی رخ می‌دهد. آیا این بدان معنا است که ذره آلفا با سرعتی بیشتر از سرعت نور از سد پتانسیل عبور می‌کند؟

اندازه‌گیری تجربی سرعت حرکت ذره کوانتومی از سد پتانسیل کار بسیار سختی خواهد بود، زیرا ساختن ساعتی با دقت زیاد برای اندازه‌گیری این پدیده بسیار سریع، کار بسیار سختی است. اما با استفاده از دستگاهی به نام «تداخل‌سنج لیگو» (Laser Interferometer Gravitational-Wave Observatory | LIGO)‌ می‌توان سرعت تونل زنی ذرات را محاسبه کرد. از این تداخل‌سنج برای کشف امواج گرانشی استفاده شد. در این آزمایش، نور لیزر توسط تقسیم‌کننده پرتو، به دو قسمت تقسیم می‌شود. سپس، پرتوهای جدا شده پس از طی کردن دو مسیر متفاوت، به یکدیگر می‌رسند. بسته‌های موج فوتون‌ها با یکدیگر تداخل می‌کنند. طرح تداخل آن‌ها، نسبت به طول مسیر پیموده شده بسیار حساس است.

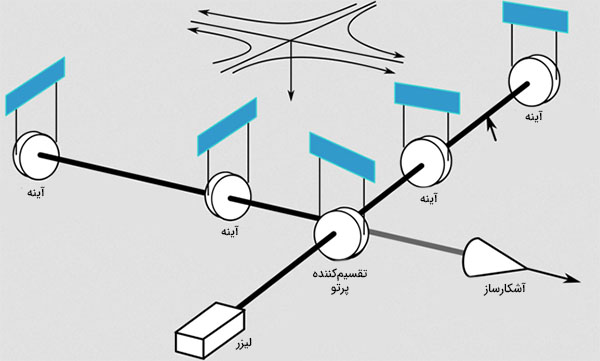
به منظور اندازه‌گیری سرعت تونل زنی کوانتومی، چیدمان تداخل‌سنج را کمی تغییر می‌دهیم. در واقع، می‌خواهیم به جای فرستادن پرتو لیزر، فوتون‌ها را به صورت تکی ارسال کنیم. همچنین، یکی از دو مسیر را با منعکس‌کننده بسیار نازکی، مسدود می‌کنیم. اگر تونل زنی کوانتومی وجود نداشت، تمام فوتون‌های رسیده به بازتاب‌کننده، منعکس می‌شدند. اما می‌دانیم تونل زنی وجود دارد. بنابراین، بسته موج فوتونی به آن سوی سد نفوذ خواهد کرد. در ۹۹٪ مواقع، فوتون منعکس می‌شود. تنها در یک درصد مواقع، فوتون در سمت دیگر سد بازتاب‌کنند‌ه یافت خواهد شد و به مسیر خود ادامه می‌دهد.

در این آزمایش، دو دسته فوتون به آشکارساز می‌رسند:

1. فوتون‌هایی که از سد بازتاب‌کننده با استفاده از تونل زنی عبور کرده‌اند.
2. فوتون‌هایی که از مسیر بدون مانع عبور می‌کنند.

اگر فوتون‌های گروه ۱ به صورت آنی از سد عبور کرده باشند، باید کمی زودتر از فوتون‌های گروه دوم به آشکارساز برسند. این تفاوت هنگامی آشکار است که بسته موج فوتون‌ها در انتها بر یکدیگر منطبق نباشند. برای این کار، مسیرهای تداخل‌سنج باید با دقت بسیار بالایی با یکدیگر برابر باشند. برای داشتن دو مسیر کاملا مساوی، باید از یکی دیگر از عجایب فیزیک کوانتوم به نام درهم‌تنیدگی کوانتومی، استفاده کنیم. برای تولید حالت‌های درهم‌تنیده، طولِ مسیرهای تداخل‌سنج باید با دقت بسیار زیادی با یکدیگر برابر و یکسان باشند. طول مسیرها را تا ظاهر شدن اثرات درهم‌تنیدگی، تنظیم می‌کنیم.

هنگامی که طول مسیرها با یکدیگر برابر شدند، هر تفاوت کوچکی در زمان طی شده توسط فوتون‌ها را می‌توانیم اندازه بگیریم. تیمی از فیزیک‌دان‌های متبحر، این آزمایش را با موفقیت انجام دادند. در این آزمایش، از سدی به ضخامت ۱/۱ میکرومتر استفاده و تاخیر زمانی تونل زنی فوتون از سد قرار گرفته در مسیر، اندازه گرفته شد. بر طبق یافته‌های این گروه، فوتون‌های تونل‌زننده کمی زودتر به آشکارساز رسیدند. بله، به نقطه‌ای رسیدیم که با فیزیک نسبیت اینشتین در تقابل است. بر طبق فیزیک نسبیت، سرعت نور، حد سرعت عالم است و هیچ چیزی سریع‌تر از نور حرکت نمی‌کند. تناقض با نسبیت تنها در اعماق فیزیک کوانتوم مشاهده شده است.

مکان هر ذره در محدوده همسایگی طول موج دوبروی آن قرار گرفته است. عدم قطعیت در مکان سبب تونل زنی کوانتومی می‌شود. فرض کنید مانعی در مسیر حرکت فوتون‌ها قرار نگرفته باشد، بی‌نظمی در مکان منجر به عدم قطعیت در زمان رسیدن فوتون می‌شود. فوتونی را در نظر بگیرید که از مسیر بدون مانعی عبور می‌کند. این فوتون می‌تواند نسبت به فوتون تونلی، زودتر برسد، زیرا بسته موج فوتون اول از گستره‌ای از مکان‌های ممکن تشکیل شده است. با قرار دادن مانع در مسیر فوتون، شکل بسته موج آن را تغییر می‌دهیم. در این حالت، تنها حالت زودتر رسیدن، انتخاب می‌شود. بنابراین، این‌گونه به نظر می‌رسد که سرعت نور افزایش یافته است.

کاربردهای تونل زنی کوانتومی چیست ؟

تونل زنی کاربردهای فراوانی در تکنولوژی، مانند فلش مموری‌ها، میکروسکوپ گتونل زنی و گسیل میدانی دارد. مهم‌ترین این کاربردها عبارت هستند از:

1. فلش مموری‌ها
2. میکروسکوپ تونل زنی
3. گسیل میدانی
4. واپاشی پرتوزایی
5. تونل زنی کوانتومی تشدیدکننده

در ادامه، در مورد هر یک از موردهای بالا توضیح می‌دهیم.

فلش مموری ها

نقش تونل زنی کوانتومی در تکنولوژی، غیرقابل‌انکار است. ترانزیستورهای اثر میدان فلز-نیمه‌هادی (Metal-Oxide-Semiconductor Fields-Effect-Transistor | MOSFET) یکی از بخش‌های مهم در میکروچیپ‌ها و کامپیوترها هستند. میکروچیپ‌ها از میلیون‌ها قطعه سیلیکون تشکیل شده‌اند. این قطعه‌های سیلیکونی در کنار یکدیگر، مدارهای مجتمع را تشکیل می‌دهند. به طور خلأصه، هر میکروچیپ، از دو قسمت تشکیل شده و مشابه کلیدی الکتریکی است:

• گیت یا دروازه کنترل
• کانال

بسته به این‌که ولتاژ الکتریکی به گیت اعمال شود یا خیر، کانال باز یا بسته خواهد بود. بنابراین، این مورد شباهت زیادی به شیر فلکه آب دارد. اندازه ولتاژ الکتریکی اعمال شده به گیت، بسیار مهم است. حالت باز یا بسته بودن گیت، به مدار، ویژگی دودویی صفر یا یک را می‌دهد.

اجازه دهید این مدار را در مقیاس فیزیکی بررسی کنیم. هنگامی که ولتاژی به دو سر گیت کنترل وارد می‌کنیم، الکترون‌ها در سطح گیت جمع می‌شوند و میدانی الکتریکی در اثر تجمع الکترون‌ها در کانال، احساس خواهد شد. میدان ایجاد شده رسانندگی کانال نیمه‌هادی را به دو صورت تغییر می‌دهد:

1. نیمه‌هادی را به رسانای خوب جریان الکتریکی تبدیل می‌کند.
2. نیمه‌هادی را عایق می‌کند. در این حالت، هیچ الکترونی از نیمه‌هادی عبور نمی‌کند.

نکته: نام اثرِ میدان برگرفته از نقش میدان، در تغییر خواص الکتریکی نیمه‌هادی است.

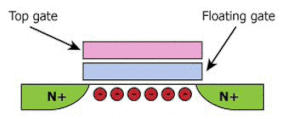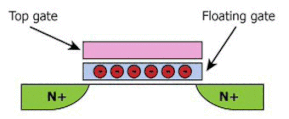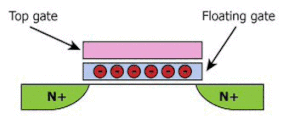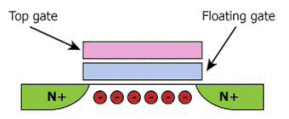
اکنون فرض کنید که الکترودِ گیت فلزی به طور مستقیم بالای کانال نیمه‌رسانا قرار می‌گرفت. هیچ تجمع الکترونی پس از اعمال ولتاژ رخ نخواهد داد، بنابراین اثر میدان مشاهده نمی‌شود. در این حالت، هر بار الکتریکی جمع‌ شده‌ای از کانال عبور خواهد کرد. این حالت را باید به گونه‌ای تغییر دهیم که بارها نزدیک کانال باشند، ولی از آن عبور نکنند. برای رسیدن به این خواسته، از لایه عایق بسیار نازکی (به طور معمول سیلیکون دی‌اکسید) استفاده می‌کنیم. شاید از خود بپرسید ارتباط کانال، گیت و ماده عایق با فلش مموری چیست. حالت صفر و یک در فلش مموری‌های با استفاده از وسیله‌ای به نام ترانزیستور گیت شناور، برقرار می‌شود. ترانزیستور گیت شناور مشابه MOSFET است، با این تفاوت که تکه‌ای فلزی یا سیلیکونی به نام گیت شناور، داخل لایه عایقی قرار گرفته می‌گیرد. چرا به آن گیت شناور گفته می‌شود؟ زیرا به جایی وصل نشده است.

عملکرد MOSFET را به یاد بیاورید. وجود یا عدم وجود بار در گیت، تعیین‌کننده باز یا بسته بود سوییچ MOSFET و در نتیجه، ایجادکننده حالت صفر و یک در مدار است. فرض کنید الکترون‌ها به گونه‌ای در گیت شناور به دام افتاده‌اند. چه اتفاقی خواهد افتاد؟ در صورتی که ولتاژ اعمال شده به مدار را قطع کنیم، اثر الکترون‌ها روی باز یا بسته بودن کانال باقی می‌ماند. در این حالت، دستگاه سوییچ نداریم، اما مموری یا حافظه داریم. وسیله می‌تواند در حالت صفر یا یک تنظیم شود و در این حالت باقی بماند. حالت دستگاه با مشاهده عبور یا عدم عبور جریان از کانال، خوانده می‌شود. در این حالت، حافظه‌ای غیرفرار داریم، یعنی با قطع ولتاژ، داده باقی خواهند ماند.

تا اینجا می‌دانیم که فلش‌ مموری‌ها چگونه کار می‌کنند. اما در نخستین مرحله‌ بارهای الکتریکی چگونه از لایه عایق عبور می‌کنند و وارد کانال می‌شوند؟ بله، تونل زنی کوانتومی دلیل اصلی عبور بارها از لایه عایق است. در واقع، این لایه همانند سد پتانسیل مقابل الکترون‌ها عمل می‌کند.

واپاشی پرتوزایی

در سال ۱۹۲۸، فردی به نام «گامو» (Gamow) تونل زنی کوانتومی را دلیل اصلی واپاشی پرتوزایی در هسته‌های اتمی دانست. گامو مشاهده کرد که ایزوتوپ‌های عناصری مانند توریوم، اورانیوم و بیسموت با تابش ذرات آلفا، فروپاشیده می‌شوند. در فرایند تابش ذره آلفا، هسته اصلی با از دست دادن دو نوترون و دو پروتون، به هسته دیگری تبدیل می‌شود. انرژی‌های جنبشی ذرات آلفای تابیده شده از ایزوتوپی مشخص، تقریبا با یکدیگر برابر هستند. اگر به تغییرات انرژی‌های جنبشی ذرات آلفای تابیده شده از ایزوتوپ‌های عناصر مختلف نگاه کنیم، کمترین انرژی در حدود ۴ مگا الکترون‌ولت و بیشترین انرژی در حدود ۹ مگا الکترون‌ولت است. بنابراین، انرژی‌های جنبشی ذرات آلفا کم‌وبیش یکسان هستند.

نیمه‌عمر ایزوتو‌پ‌های مختلف بسیار متفاوت است. به عنوان مثال، نیمه‌عمر پلونیوم-۲۱۴ برابر ۱۶۰ میکروثانیه و نیمه‌عمر اورانیوم، برابر ۴/۵ میلیارد سال است. گامو برای توضیح این تغییر، مدل جعبه کروی هسته را پیشنهاد داد. ذرات آلفا در این کره همانند ذرات آزاد بین دیواره‌های جعبه حرکت می‌کنند. سوالی که ممکن است مطرح شود آن است که نقش پتانسیل هسته‌ای قوی چیست. در فرض مدل جعبه کروی هسته، دیواره‌های کره نقش پتانسیل هسته‌ای را ایفا می‌کنند. به این نکته توجه داشته باشید که دیواره‌ها نامحدود نیستند، بنابراین، ذره هسته‌ای شانس فرار از زندان هسته‌ای را خواهد داشت.

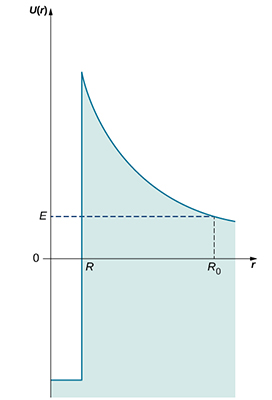
فرض کنید ذره آلفا از زندان هسته‌ای فرار کرده است، نیروی دافعه الکترواستاتیکی در بیرون جعبه کروی، ذره را از هسته دور می‌کند. عرض سد پتانسیل جداکننده ذره آلفا از محیط بیرون، به انرژی جنبشی ذره، یعنی E، بستگی دارد و به صورت زیر تعریف می‌شود:

$$L = R_0 - R$$

در رابطه فوق:

• $$R$$ برابر شعاع هسته است.
• $$R_0$$ برابر مکان ذره آلفا، بیرون سد پتانسیل است.

در نقطه $$R_0$$، انرژی جنبشی ذره باید حداقل با انرژی دافعه الکترواستاتیکی هسته مطابقت داشته باشد.

$$E =\frac{1 }{4 \pi \epsilon_0} \frac{Z e^ 2} {R _ 0}$$

در رابطه فوق، $$+ \ Ze$$ بار هسته است. با در نظر گرفتن رابطه‌های فوق، عرض سد هسته‌ای به صورت زیر نوشته می‌شود:

$$L = \frac{1 }{4 \pi \epsilon_0} \frac{Z e^ 2} {R _ 0} - R$$

با توجه به رابطه بالا، هر چه انرژی جنبشی ذره آلفا بیشتر باشد، عرض سد هسته‌ای کمتر خواهد بود. عرض سد پتانسیل، مهم‌ترین عامل در احتمال تونل زنی کوانتومی است. از این‌رو، ذرات آلفای پرانرژی با احتمال بالایی از هسته فرار می‌کنند. بنابراین، طول عمر چنین هسته‌ای بسیار کوتاه است. به این نکته توجه داشته باشید که درصد غیرخطی بودن این فرایند بسیار بالا است. در نتیجه، اگر انرژی جنبشی ذره آلفا مقدار کمی زیاد شود، احتمال تونل‌زنی بسیار زیاد و طول عمر کوتاه می‌شود. اکنون می‌توانیم دلیل طول عمر کوتاه پلونیوم و طول‌ عمر بلند اورانیوم را توضیح دهیم.

گسیل میدانی

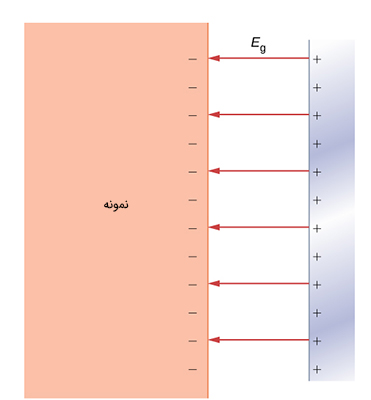
سطح رسانایی را در نظر بگیرید. اگر میدان الکتریکی بسیار قوی را به صورت عمود بر سطح رسانا بتابانیم و الکترون‌ها از این سطح خارج شوند، گسیل میدانی اتفاق افتاده است. میدان الکتریکی خارجی، سبب حرکت الکترون‌ها به سطح رسانا می‌شود و تا زمانی که میدان خارجی به اندازه کافی قوی نباشد، در سطح رسانا باقی می‌مانند. در این حالت، مقدار پتانسیل الکتریکی داخل رسانا و سطح آن ثابت است. به تصویر زیر توجه کنید. میدان الکتریکی خارجی ثابت و مقدار آن برابر $$E_g$$ است. اگر الکترونی به صورت اتفاقی خارج رسانا و در فاصله x از سطح آن قرار داشته باشد، انرژی پتانسیل به صورت زیر نوشته می‌شود:

$$U(x) = - \ e E_g x$$

در رابطه فوق، x فاصله از سطح رسانا است.

سطح رسانا را مبدأ مختصات در نظر بگیرید. انرژی پتانسیلِ الکترون‌های داخل فلز را می‌توانیم به عنوان سد انرژی پتانسیل نشان داده شده در تصویر زیر، در نظر بگیریم. در غیاب میدان الکتریکی خارجی، سد پتانسیل به سدی پله‌ای تبدیل و به صورت زیر تعریف می‌شود:

$$U ( x \leq 0) = - \ U_ 0, \ \ U(x > 0) = 0$$

اگر میدان الکتریکی خارجی بسیار قوی باشد، الکترون‌های رسانای قرار گرفته در سطح ممکن است از سطح کنده شوند و در امتداد خطوط میدان الکتریکی و در جهت مخالف آن، شتاب بگیرند. به بیان دیگر، الکترون‌های رسانا به داخل سد پتانسیل، سطح فلز، تونل زده‌اند. فرایند حاکم بر گسیل میدانی شباهت بسیاری به فرایند تابش ذرات آلفا از هسته پرتوزا دارد.

فرض کنید انرژی جنبشی الکترون برابر $$E$$ باشد، و میدان الکتریکی خارجی به صورت موضعی ثابت و مقدار آن برابر $$E_g$$ است. عرض سد پتانسیل برابر فاصله بین سطح رسانا و نقطه‌ای خارج از سطح است که در آنجا انرژی جنبشی الکترون با مقدار انرژی پتانسیل آن در میدان خارجی، مطابقت دارد. در شکل زیر، این فاصله در امتداد خط افقی خط‌چین اندازه گرفته می‌شود. عرض سد پتانسیل را به صورت زیر می‌توان نوشت:

$$L = \frac{e^{- 1} E}{E_g} = \frac{e^{-1} \phi}{E_g}$$

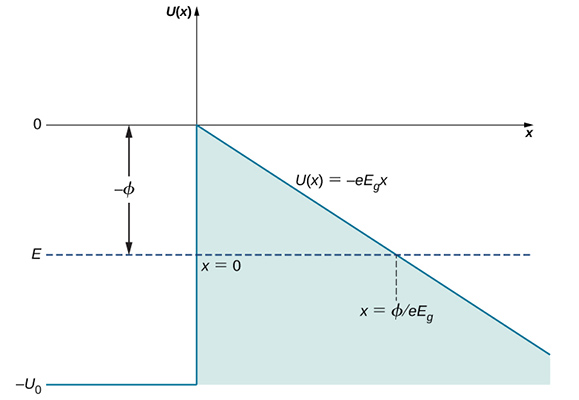
همان‌طور که در رابطه نوشته شده برای عرض چاه پتانسیل دیده می‌شود، $$L$$ به صورت معکوس با قدرت میدان الکتریکی خارجی، $$E _ g$$ متناسب است. هنگامی که قدرت میدان خارجی را افزایش می‌دهیم، شیب پتانسیل الکتریکی بیرون رسانا تندتر و در نتیجه، عرض آن کاهش می‌یابد. از این‌رو، عبور الکترونی با انرژی جنبشی مشخص از سد پتانسیل، آسان‌تر خواهد بود. الکترون‌های عبورکننده از سد، جریان عبوری را تشکیل می‌دهند (جریان تونلی الکترون). احتمال تونل زنی به صورت غیرخطی به طول سد، $$L$$ بستگی دارد و $$L$$ با تغییر شدت میدان الکتریکی خارجی تغییر می‌کند. بنابراین، جریان تونلی الکترون با تغییر شدت میدان الکتریکی خارجی در سطح، تغییر خواهد کرد.

میکروسکوپ تونل زنی روبشی

میکروسکوپ‌ها انواع مختلفی دارند:

• میکروسکوپ‌های نوری
• میکروسکوپ‌های الکترونی

الکترون‌ها در میکروسکوپ‌های الکترونی مانند ذره رفتار می‌کنند. به عنوان مثال، همانند ذره به سطح ماده برخورد می‌کنند و منعکس می‌شوند. تحلیل الکترون‌های بازتابی، اطلاعاتی را در مورد ساختار ماده موردمطالعه می‌دهد. اما الکترون‌های استفاده شده در میکروسکوپ تونلی به صورت موجی رفتار می‌کنند. بنابراین، تونل زنی کوانتومی اساس کار میکروسکوپ‌های تونلی است.

«از میکروسکوپ تونلی روبشی» (Scanning Tunneling Microscopy | STM) برای مطالعه سطح مواد مختلف، مانند طلا و گرافیت، استفاده می‌شود. این میکروسکوپ کاربرد زیادی در علم نانو دارد. یکی از قسمت‌های این میکروسکوپ، سوزنی فلزی با رسانایی بالای جریان الکتریکی و حامل تعداد زیادی الکترون است. سوزن را با استفاده از مدار الکتریکی به ماده موردمطالعه وصل و ولتاژی با اندازه مشخص بر مدار وارد می‌کنیم. جریان الکتریکی بین نمونه و سوزن برقرار می‌شود. به بیان دیگر، به دلیل برقراری ولتاژ بین نمونه و سوزن، جریان بین نمونه و سوزن به صورت موج جریان می‌یابد.

مقدار الکتریسیته ایجاد شده بین نمونه و سوزن به صورت معکوس متناسب با اندازه ولتاژ است. اگر مقدار ولتاژ اعمال شده بزرگ باشد، تعداد الکترون آزاد شده از نوک سوزن کم خواهد بود. در مقابل، اگر مقدار ولتاژ اعمال شده کوچک باشد، مقدار جریان یا تعداد الکترون‌های آزاده شده از نوک سوزن زیاد است. به طور معمول، سوزن استفاده شده در این میکروسکوپ از تنگستن ساخته می‌شود.

گفتیم STM از سوزنی بسیار تیز برای مطالعه سطح ماده موردنظر استفاده می‌کند. سوزن در فاصله خیلی نزدیک از سطح قرار می‌گیرد و ولتاژ الکتریکی بین سوزن و سطح نمونه، اعمال می‌شود. تصویر گرفته شده توسط STM حتی می‌تواند سطح را تا مقیاس اتمی نشان دهد. عملکرد STM بر پایه چند اصل است:

• تونل زنی کوانتومی: با استفاده از این اثر می‌توان سطح را مشاهده کرد.
• اثر پیزوالکتریک: با استفاده از این اثر می‌توان سطح را تا مقیاس اتمی روبش و مشاهده کرد.
• حلقه بازخورد: این حلقه جریان تونلی را کنترل و مکان سوزن و جریان را هماهنگ می‌کند.

عملکرد میکروسکوپ تونلی روبشی در تصویر زیر نشان داده شده است. تونل زنی از سطح سوزن به سطح نمونه رخ می‌دهد.

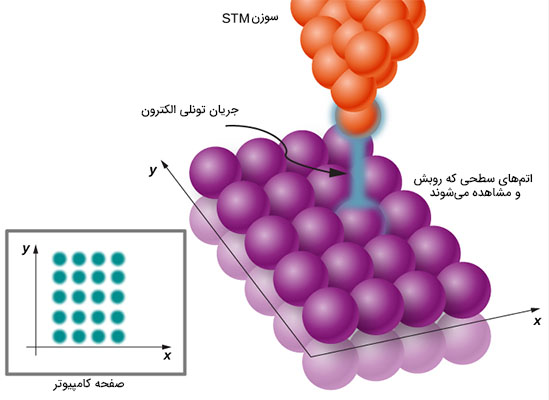
جریان تونلی هنگامی اتفاق می‌افتد که الکترون‌ها از سدی عبور کنند که به صورت کلاسیکی نمی‌توانستند از آن بگذرند. در فیزیک نیوتنی یا کلاسیک، اگر انرژی جنبشی الکترونی به اندازه کافی برای عبور از سد پتانسیل، بزرگ نباشد، از سد عبور نخواهد کرد. اما در فیزیک کوانتوم الکترون رفتار موج-ذره‌ای از خود نشان می‌دهد. موج نسبت داده شده به الکترون به هنگام برخورد به دیواره سد، ناپدید نمی‌شود، بلکه به سرعت افت می‌کند. اگر عرض سد به اندازه کافی باریک باشد، تابع احتمال ممکن است به سمت دیگر آن، گسترش یابد. احتمال یافتن الکترون در سمت دیگر سد، کوچک است. اما اگر الکترون‌های زیادی را جلوی سد پتانسیل قرار دهیم، برخی از آن‌ها به طور حتم پس از تونل زنی، در سمت دیگر دیوار سد مشاهده خواهند شد.

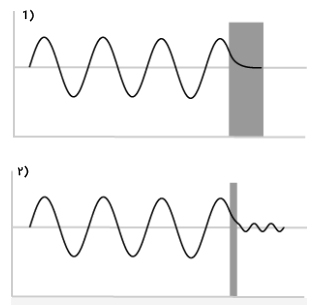
به تصویر نشان داده شده در بالا دقت کنید. در عکس شماره یک، عرض سد پتانسیل زیاد است. بنابراین، موج پس از برخورد با دیواره سد، به داخل آن نفوذ و به سرعت افت می‌کند. در واقع، موج به سمت دیگر سد نفوذ نکرده است. در مقابل، اگر عرض سد به اندازه کافی کوچک باشد، قسمتی از موج پس از افت داخل سد، به سمت دیگر آن خواهد رفت. بنابراین، تعدادی الکترون در سمت دیگر سد مشاهده خواهند شد. تصویر STM گرفته شده از نانولوله کربنی در شکل زیر نشان داده شده است. با این وسیله می‌توان سطح را در مقیاس اتمی بررسی کرد. توجه به این نکته مهم است که عکس‌های گرفته شده توسط ‌STM، خاکستری هستند و رنگ برای نشان دادن جزییات به آن اضافه می‌شود.

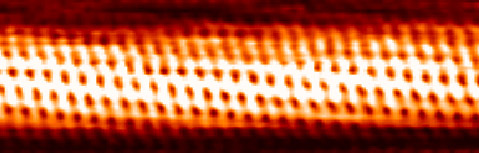
از آنجا که شدت تابع احتمال، داخل سد به شدت کاهش می‌یابد، تعداد الکترون‌های ظاهر شده در سمت دیگر سد به شدت به عرض آن بستگی دارند. اکنون این توضیحات را در مورد میکروسکوپ STM استفاده می‌کنیم. نقطه آغازِ الکترون، سوزن است یا سطح نمونه. نقطه شروع به چیدمان دستگاه وابسته خواهد بود. شکاف بین نمونه و سوزن، همان سد پتانسیل است. این شکاف ممکن است هوا، خلأ یا مایع باشد. ناحیه دوم پس از سد، سوزن یا سطح نمونه است. سوالی که ممکن است مطرح شود آن است که چگونه فاصله بین سوزن و نمونه تنظیم می‌شود. برای انجام این کار کافی است جریان عبوری از شکاف، کنترل شود.

تونل زنی کوانتومی تشدیدکننده

همان‌طور که گفته شد تونل زنی کوانتومی کاربردهای متعددی در وسایل نیمه‌هادی، مانند عناصر تشکیل دهنده مدار یا مدارهای مجتمع به کار رفته در مقیاس نانو، دارد. به عنوان مثال، دیود را می‌توان به عنوان اتصال تونلی بین دو نوع ماده نیمه‌رسانا در نظر گرفت. در این دیود تونلی، الکترون‌ها از میان سد پتانسیل تکی در محل اتصال بین نیمه‌رساناهای متفاوت، تونل می‌زنند. در نقطه اتصال، جریان تونلی الکترون به صورت غیرخطی با اختلاف پتانسیل اعمال شده در محل اتصال، تغییر خواهد کرد. اگر مقدار ولتاژ بایاس کاهش یابد، اندازه جریان تونلی به شدت کاهش می‌یابد. این رفتار هیچ شباهتی با قانون اهم ندارد، زیرا در مقیاس کوانتومی و با پدیده‌ای به نام تونل زنی کوانتومی روبرو هستیم.

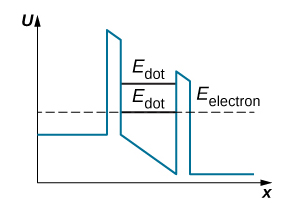
در نوع دیگری از وسایل نانوالکترونیک به نام نقطه‌های کوانتومی، از تونل زنی تشدیدی الکترون‌ها استفاده می‌شود. نقطه کوانتومی ناحیه بسیار کوچکی از نانوکریستال نیمه‌رسانایی است که روی سطح مناسبی مانند سیلیکون یا کریستال آلومینیوم آرسنید، رشد کرده است. در تصویر زیر، نقطه کوانتومی از جنس گالیم آرسنید، داخل آلومینیوم آرسنید را مشاهده می‌کنید.

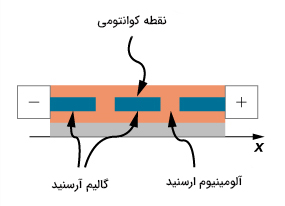
ناحیه مربوط به نقطه کوانتومی به عنوان چاه پتانسیلی با ارتفاع محدود عمل می‌کند. ذره کوانتومی محبوس در چاه پتانسیل با ارتفاع نامحدود را در نظر بگیرید. انرژی‌‌های محاسبه شده برای این ذره، گسسته هستند. به طور مشابه، انرژی ذره محبوس در چاه پتانسیلی با ارتفاع محدود نیز گسسته است. تفاوت بین پتانسیل‌های چاه و جعبه در آن است که تعداد انرژی‌های گسسته ذره کوانتومی در جعبه، نامحدود است و برای همیشه در جعبه قرار دارد. در مقابل، سطوح انرژی گسسته ذره کوانتومی محبوس در چاه پتانسیل، محدود است و این ذره می‌تواند با استفاده از تونل زنی کوانتومی به بیرون چاه برود. از این‌رو، نقطه کوانتومی گالیم آرسنیدِ قرار گرفته در آلومینیوم آرسنید، چاه پتانسیلی است که انرژی‌های الکترون در ترازهای پایین ($$E_{dot}$$، گسسته هستند.

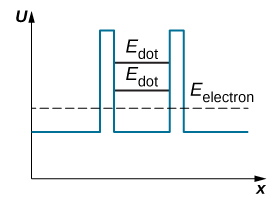
اگر انرژی الکترون، $$E_{electron}$$، در قسمت بیرونی نقطه کوانتومی با انرژی آن داخل نقطه، $$E _ { dot}$$، هم‌خوانی نداشته باشد، الکترون نمی‌تواند از داخل نقطه، تونل بزند. بنابراین، حتی اگر اختلاف پتانسیلی به نقطه کوانتومی وارد شود، هیچ جریان عبوری وجود نخواهد داشت. اگر مقدار ولتاژ‌ بایاس به گونه‌ای عوض شود که ارتفاع یکی از دیواره‌های سد پتانسیل کمتر از دیوار دیگر شود، انرژی‌های $$E _ { dot}$$ و $$E_{electron}$$ هم‌خط یا تراز می‌شوند. بنابراین جریان از نقطه کوانتومی عبور خواهد کرد.

تونل زنی کوانتومی در طبیعت

گرچه ممکن است تونل زنی کوانتومی کاربرد خاصی در زندگی روزمره نداشته باشد، این پدیده یکی از فرایندهای بنیادی در طبیعت است. بر طبق فرضیه مطرح شده توسط بسیاری از دانشمندان، تونل زنی کوانتومی دلیل اصلی گذر کیهان از حالت بدون هندسه (بدون فضا-زمان) به حالتی شد که فضا، زمان، ماده و زندگی به وجود آمد.

تونل زنی در همجوشی ستاره ای

همجوشی فرایندی است که در آن هسته‌های کوچک‌تر به یکدیگر متصل می‌شوند و هسته بزرگ‌تری در تشکیل می‌دهند. این فرایند با آزادسازی مقدار قابل‌توجهی انرژی همراه است. همجوشی داخل ستاره‌ها، همه عناصر جدول تناوبی، به جز هیدروژن، را تولید می‌کند. انرژی ستاره‌ها از همجوشی هیدروژن به هلیوم، به‌دست می‌آید.

همجوشی بیشتر از آنچه تصور می‌شود، در طبیعت رخ می‌دهد. از آنجا که همه هسته‌های اتمی بار مثبت دارند، نیروی دافعه بین آن‌ها به شدت قوی است. همچنین، انرژی جنبشی هسته‌ها به‌ ندرت بر نیروی دافعه قوی بین آن‌ها غلبه می‌کند. از این‌رو، این‌گونه به نظر می‌رسد که همجوشی هسته‌ای به راحتی اتفاق نمی‌افتد. اگر تونل زنی کوانتومی را در همجوشی هسته‌ای در نظر بگیریم، درصد هسته‌های هیدروژن که وارد این واکنش می‌شوند به میزان قابل‌توجهی افزایش خواهد یافت. بنابراین، پایداری ستاره‌ها در طول میلیون‌ها سال قابل توجیه است. اما این فرضیه از نظر علمی به طور کامل اثبات نشده است، زیرا هسته هیدروژن قبل از همجوشی با هسته دیگر، صدها برخورد رو در رو انجام می‌دهد.

تونل زنی در گیرنده های بویایی

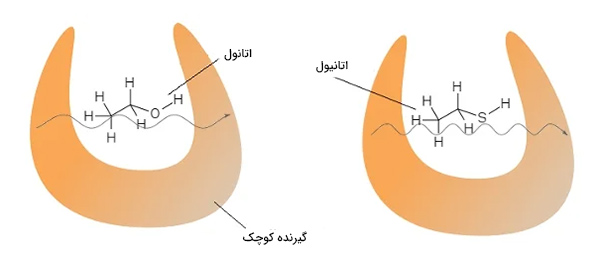
گیرنده‌های شیمیایی در بینی (۴۰۰ نوع در انسان) وجود مواد شیمیایی مختلف را با استفاده از فرایند قفل و کلید، تشخیص می‌دهند. این فرایند، شکل فیزیکی مولکول را شناسایی می‌کند. اما پژوهش‌های انجام شده در سال‌های اخیر، این نظریه را زیر سوال برده است. به عنوان مثال، دو ماده شیمیایی اتانول و اتانیول دارای شکل‌های بسیار شبیه به هم و بوهای بسیار متفاوت هستند. این نشان می‌دهد که مکانیسم شناسایی دیگری استفاده می‌شود.

بر طبق نظریه‌های جدید مطرح شده، گیرنده‌های کوچک در بخشی از فرایند شناسایی مواد شیمیایی، از تونل زنی کوانتومی استفاده می‌کنند. گیرنده‌‌ها، جریان کوچکی را به مولکول بو ارسال می‌کنند و سبب ارتعاش آن با فرکانس مشخصی می‌شوند. برای برقراری جریان الکتریکی، الکترون‌ها باید از میان شکاف نارسانای بین سلول‌های گیرنده و مولکول، تونل بزنند. در آزمایش‌های جدید انجام شده روی تونل زنی کوانتومی، از پیوندهای بزرگ هیدروژن و دوتریوم برای تسهیل واکنش‌های بویایی به محرک‌ها، استفاده شد. نتایج به‌دست آمده نشان می‌دهد انسان‌ها قادر به تشخیص مولکول‌هایی با ارتعاش کوانتومی مشخص، هستند.

اصل عدم قطعیت هایزنبرگ چیست ؟

اصل عدم قطعیت هایزنبرگ، یکی از اصول فیزیک کوانتوم است که توسط هایزنبرگ در حدود ۱۰۰ سال قبل مطرح شد. اینشتین یکی از مخالفان سرسخت این اصل بود، ولی بعدها مجبور به پذیرش آن شد. بر طبق این اصل، به طور همزمان نمی‌توانیم مکان و سرعت دقیق ذره‌ای را داشته باشیم. به بیان دیگر، دانستن همزمان متغیرهای مرتبط با یکدیگر امکان‌پذیر نیست. در اکثر موارد، اصل عدم قطعیت برای مکان و تکانه (سرعت) ذره به کار برده می‌شود.

عدم قطعیت در مکان را با $$\Delta x$$ و عدم قطعیت در تکانه را با $$\Delta p$$ نشان می‌دهیم. حاصل‌ضرب این دو به صورت زیر نوشته می‌شود:

$$\Delta x \times \Delta p \ \geq \frac{\hbar}{2}$$

$$\hbar$$ تنها یک عدد است و به ثابت پلانک مربوط می‌شود. رابطه فوق به ما می‌گوید هنگامی که عدم قطعیتِ دو ویژگی از یک ذره را با یکدیگر ضرب کنیم، نتیجه برابر یا بزرگ‌تر از عددی مشخص خواهد بود. به بیان دیگر، حاصل‌ضرب دو عدم قطعیت در یکدیگر حداقل باید برابر $$\frac {hbar} {2}$$ باشد. اما این جمله چه معنایی دارد؟ معنای آن این است که نمی‌توانیم عدم قطعیت دو کمیت را همزمان، هر چقدر که می‌خواهیم کوچک کنیم. فرض کنید $$\Delta x$$ را بسیار کوچک می‌کنیم. به بیان دیگر مکان ذره را با دقت خوبی اندازه می‌گیریم. در این حالت، برای برقرار نامساوی، مقدار $$\Delta p$$ باید بسیار بزرگ باشد. توجه به این نکته مهم است که منظور از عدم قطعیت، عدم قطعیت در اندازه‌گیری مکان یا سرعت است.

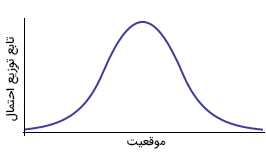
در فیزیک کلاسیک، مکان ذره را می‌توان به طور دقیق مشخص کرد، اما در فیزیک کوانتوم، مکان ذره با احتمال مشخص می‌شود. در فیزیک کوانتوم، قبل از آن‌که مکان ذره را اندازه بگیریم، تابع توزیع احتمال مربوط به ذره موردنظر را داریم. تابع احتمال نشان داده شده در تصویر زیر را در نظر بگیرید. پیک تابع نشان‌ می‌دهد که ذره با احتمال زیادی در مکان $$x$$ قرار گرفته است. بر طبق نمودار، ذره با احتمال کمتری در مکان‌های دیگر نیز می‌تواند قرار داشته باشد. عرض تابع توزیع احتمال بیان‌کننده عدم قطعیت در اندازه‌گیری مکان ذره است. ذکر این نکته مهم است که مقدار عدم قطعیت در مکان یا سرعت ذره، هیچ‌گاه صفر نمی‌شود. اگر عدم قطعیت در مکان ذره برابر صفر شود، عدم قطعیت در تکانه آن، بی‌نهایت خواهد شد. به بیان دیگر، اگر مکان ذره را به طور دقیق بدانیم، در مورد سرعت یا تکانه آن هیچ چیزی نمی‌توانیم بگوییم.

ذره‌ای را در نظر بگیرید که آزادانه در فضا حرکت می‌کند. مکان و سرعت این ذره را چگونه اندازه می‌گیریم؟ با خط‌کش؟ خیر، در مورد ذره‌ای در مقیاس کوانتومی صحبت می‌کنیم. برای اندازه‌گیری مکان این ذره، به آن نور می‌تابانیم. نور پس از برخورد به ذره، از آن منعکس می‌شود و اطلاعاتی در مورد مکان یا سرعت ذره به ما می‌دهد. هر چه اندازه ذره کوچک‌تر شود، به دنیای کوانتوم نزدیکتر می‌شویم. در مقیاس کوانتومی باید به ویژگی‌های کوانتومی نور توجه کنیم، رفتار دوگانه موج-ذره. نور هم رفتار موجی دارد هم رفتار ذره‌ای. به بیان دیگر، نور از بسته‌هایی به نام فوتون تشکیل شده است. اگر نور را به عنوان موج در نظر بگیریم، برای آن فرکانس و طول موج تعریف می‌کنیم.

اگر طول موج نور تابیده شده به ذره کوتاه باشد، اطلاعات بیشتری در مورد مکان ذره به دست خواهیم آورد. اما، به یاد داشته باشید هرچه طول موج کوچک‌تر باشد، انرژی ذره بیشتر خواهد بود. رابطه زیر را در نظر بگیرید:

$$E = \frac {hc} {\lambda }$$

در رابطه فوق:

• $$E$$ مقدار انرژی نور است.
• $$hc$$ حاصل‌ضرب دو ثابت و مقدار آن نیز ثابت است.
• $$\ lambda$$ طول موج نور است.

از آنجا که $$hc$$ ثابت است، انرژی با $$\frac {1} {\lambda}$$ متناسب است. بنابراین، اگر طول موج نور کوتاه باشد، انرژی آن زیاد و برعکس اگر طول موج بلند باشد، انرژی نور کم است. در نتیجه، اگر نوری با انرژی زیاد به ذره‌ای کوانتومی بتابد، همانند این است که به ذره ضربه محکمی وارد می‌شود. از آنجا که ضربه محکمی به ذره وارد شده است، اندازه‌گیری سرعت حرکت آن به طور دقیق امکان‌پذیر نخواهد بود. اما این توضیحِ اصل عدم قطعیت هایزنبرگ نیست. هایزنبرگ برای توضیح چرایی وقوع عدم قطعیت، این توضیح را ارائه داد. سوالی که ممکن است مطرح شود آن است که این اصل واقعا از کجا می‌آید.

اصل عدم قطعیت هایزنبرگ از کجا می آید ؟

برای پاسخ به این سوال، باید کمی وارد مبحثی از ریاضیات به نام تبدیل فوریه شویم. بسیاری از توابع ریاضی می‌توانند به توابع پایه، شکسته و برحسب آن‌ها نوشته شوند. برای درک بهتر این مفهوم، به مبحث دیگری در ریاضیات، بردارها، نگاهی می‌اندازیم. بردارها، اندازه و جهت دارند. بردار در نقطه مشخصی شروع و در نقطه مشخص دیگری تمام می‌شود. از فیزیک پایه به یاد داریم که بردارها را می‌توان برحسب مولفه‌های برداری نوشت. به عنوان مثال، بردار را می‌توان به مولفه عمودی و افقی تجزیه کرد. فرض کنید برداری با اندازه ۵ واحد داریم. این بردار را به صورت نشان داده شده در تصویر، به مولفه‌های عمودی و افقی تجزیه می‌کنیم. اندازه موله افقی آن برابر ۳ واحد و مولفه عمودی آن برابر ۴ واحد است. زاویه بین مولفه‌های افقی و عمودی برابر ۹۰ درجه است.

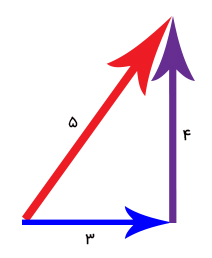
بردار فوق را به دو بردار عمودی و افقی یا بردارهای سازنده، تجزیه کردیم. اگر بردار واحد در راستای محور افقی را با $$\rightarrow$$ و بردار واحد در راستای عمودی را با $$uparrow$$ نشان دهیم، بردار نشان داده شده در تصویر را می‌توان به صورت زیر نوشت:

$$\overrightarrow{5} = 3 \rightarrow + \ \ 4 \downarrow$$

توابع ریاضی نیز مانند بردارها می‌توانند به توابع سازنده، تجزیه شوند. در حالت کلی، توابعی که به عنوان توابع پایه استفاده می‌شوند، سینوسِ فرکانس‌های مختلف هستند. همچنین، دامنه این توابع را واحد در نظر می‌گیریم. تابع موردنظر را برحسب این توابع سینوسی می‌نویسیم یا به عبارتی بسط می‌دهیم. همانند بردارها، یک تابع اصلی داریم که آن را برحسب توابع سینوسی در فرکانس‌های مختلف می‌نویسیم. توجه به این نکته مهم است که وزن هر تابع سینوسی ممکن است متفاوت با وزن تابع دیگر باشد. تابعی دلخواهی را در نظر بگیرید که آن را برحسب توابع سینوسی با دامنه واحد و فرکانس‌های مختلف می‌نویسیم. تابع موردنظر به صورتی که در تصویر نشان داده شده است، برحسب توابع سینوسی واحد نوشته می‌شود.

کاری که می‌توان انجام داد، رسم تابع جدید است. ابتدا محورهای عمودی و افقی را رسم می‌کنیم. محور افقی برحسب فرکانس‌های توابع سینوسی واحد و محور عمودی بر حسب ضریب‌های هر تابع سینوسی است. این تابع رسم شده همان تبدیل فوریه تابع اولیه است. قبل از آن‌که تبدیل فوریه را به اصل عدم قطعیت هایزنبرگ ربط دهیم، به این نکته توجه کنید. اگر گستردگی تابع اولیه در راستای محور افقی، زیاد باشد، تبدیل فوریه آن در راستای محور افقی، باریک خواهد شد. این یکی از ویژگی‌های مهم تبدیل فوریه است.

تابع $$\sin ( x)$$ را در نظر بگیرید. اگر این تابع را به توابع سازنده آن بشکنیم، به خود تابع سینوس می‌رسیم. فرکانس تابع سینوس اولیه و تابع تشکیل‌دهنده آن برابر f است. تابع $$\sin ( x)$$ در راستای محور افقی، به سمت راست یا چپ، تا بی‌نهایت گسترش یافته است. اکنون تابع تبدیل فوریه آن را رسم می‌کنیم. با توجه به تصویر نشان داده شده در ادامه، تابع سری فوریه $$\sin ( x)$$ در راستای محور افقی، بی‌نهایت باریک است. بنابراین، تبدیل فوریه، گستردگی تابع اولیه را در راستای مشخص می‌گیرد.

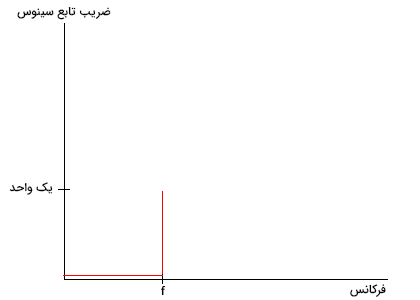
شاید از خود پرسیده باشید تبدیل فوریه و اصل عدم قطعیت هایزنبرگ، چه ربطی با یکدیگر دارند. برای پاسخ به این پرسش، به یاد بیاورید که موقعیت مکانی و تکانه ذره کوانتومی با استفاده از توزیع احتمال توصیف می‌شوند. به بیان دیگر، احتمال‌های مشخصی برای موقعیت مکانی یا تکانه ذره کوانتومی داریم که در محدوده معینی قرار گرفته‌اند. توزیع احتمال این دو کمیت در تابعی به نام تابع موج قرار می‌گیرند. به هدف نزدیک شدیم. تابع موج تکانه ذره، تبدیل فوریه تابع موج مکان ذره است. اگر تابع موج ذره گسترده باشد، اطلاعات کمی در مورد موقعیت مکانی ذره خواهیم داشت. زیرا تابع موج مکان، مقدارهای مختلفی دارد. در مقابل، تابع موج تکانه ذره، بسیار باریک است. به بیان دیگر، در مورد تکانه ذره با قطعیت بیشتری صحبت خواهیم کرد.

اصل عدم قطعیت هایزنبرگ، یکی از مهم‌ترین ویژگی‌های کیهان است. این اصل، هیچ ربطی به وسیله اندازه‌گیری یا تکنولوژی مورداستفاده به هنگام اندازه‌گیری مکان یا تکانه ندارد.

زمان تونل زنی کوانتومی

تونل زنی کوانتومی یکی از عجیب‌ترین دستاوردهای فیزیک کوانتوم است. در مطالب بالا در مورد برخی از کاربردهای مهم تونل زنی در طبیعت و در صنعت الکترونیک صحبت کردیم. تونل زنی ذرات کوانتومی از سد پتانسیل، به دلیل خاصیت موجی آن‌ها و اصل عدم قطعیت هایزنبرگ است. سوالی که در میان دانشمندان مطرح شده آن است که آیا تونل زنی، اتفاقی آنی است یا زمان بسیار کوتاهی برای وقوع آن باید در نظر گرفت. بر طبق پژوهش‌های به‌دست آمده، اندازه‌گیری زمان تونل‌ زنی، بسیار سخت و چالش‌برانگیز است. زیرا در دنیای برهم‌ریخته کوانتوم، حتی تعریف معنای زمان تونل زنی بسیار سخت خواهد بود. اما نکته مهمی در اینجا وجود دارد. تعریف‌های مختلفی برای زمان تونل زنی کوانتومی ارائه شده است و در همه آن‌ها سرعت بیش‌تر از سرعت نور، مشترک به نظر می‌رسد.

در سال ۱۹۶۲، فیزیک‌دانی به نام «توماس هارتمن» (Thomas Hartman) ادعا کرد که زمان لازم برای تونل زنی می‌تواند مستقل از ضخامت سد پتانسیل باشد. به بیان دیگر، زمان تونل زنی ذره کوانتومی از سدی به ضخامت L، برابر زمانی است که همان ذره از سدی به ضخامت $$2L$$، تونل می‌زند. بر طبق این ادعا، حرکت سریع‌تر از سرعت نور می‌تواند وجود داشته باشد. اما اینشتین هیچ‌گاه طرفدار این نظریه نبود. از نظر او، هیچ چیز در طبیعت نمی‌تواند سریع‌تر از سرعت نور، حد سرعت در عالم، حرکت کند. بر طبق نسبیت خاص اینشتنن، حرکت با سرعتی سریع‌تر از سرعت نور برابر فرستادن سیگنال به گذشته و خلق تضادهای بسیار است.

در مطالب بالا توضیح دادیم که چرا این اثر با نسبیت خاص اینشتین در تضاد نیست. پاسخ در تعریف زمان تونل زنی نهفته است. اگر مکان ذره کوانتومی به طور دقیق مشخص نباشد، چگونه و از کجا باید زمان شروع حرکت و پایان آن را مشخص کنیم؟ می‌دانیم ذره کوانتومی به صورت تابع موج توصیف می‌شود. بنابراین، زمان تونل زنی به صورت مدت زمان عبور مرکز تابع موج از نقطه‌های آغاز و پایان، تعریف می‌شود. اگر شکل تابع موج به هنگام تونل زنی تغییر کند، چه می‌توان کرد؟ در واقع، لبه پیشروی تابع موج قدیمی، به مرکز تابع موج جدید تبدیل می‌شود. برای درک بهتر این مفهوم به مثال زیر توجه کنید.

زمان عبور قطاری داخل تونل را اندازه بگیرید:

• هنگامی که مرکز قطار وارد تونل شد، کرنومتر را روشن کنید.
• هنگامی که جلوی قطار از تونل خارج شد، کرنومتر را خاموش کنید.

زمانی را که اندازه می‌گیرید با $$t_1$$ نشان دهید. به هنگام اندازه‌گیری زمان $$t_1$$، دو نقطه متفاوت از قطار در نظر گرفته شد. اکنون دو نقطه یکسان را برای اندازه‌گیری زمان عبور قطار از داخل تونل انتخاب کنید و آن را $$t_2$$ بنامید. با مقایسه زمان‌های اندازه‌گیری شده، متوجه خواهید شد که $$t_۲$$ از $$t_1$$ بزرگ‌تر است.

اکنون فرض کنید، قطار گفته شده در مثال بالا، قطار کوانتومی است و از قوانین حاکم بر فیزیک کوانتوم پیروی می‌کند. در این حالت، تنها لبه جلویی قطار از تونل عبور خواهد کرد و مابقی قطار به سمت عقب برمی‌گردد (این حالت شبیه بازتاب بخشی از موج پس از برخورد به سد پتانسیل است). بنابراین، تنها جلوی قطار را مشاهده خواهید کرد. بنابراین، اندازه‌گیری زمان عبور از تونل برای قطار کوانتومی یا تابع موج کوانتومی بسیار سخت است، زیرا مشخص کردن نقاط ابتدا و انتها بسیار سخت خواهد بود.

تا اینجا متوجه شدیم که پرسش مطرح شده در مورد زمان تونل زنی کوانتومی کمی گمراه‌کننده است. برای پاسخ به این پرسش، باید پرسش بهتری را تعریف کنیم. دو نقطه را در دو حالت در نظر بگیرید:

• حالت اول: دو نقطه توسط مانعی از یکدیگر جدا شده‌اند.
• حالت دوم: دو نقطه در خلأ قرار گرفته‌اند.

پیغامی را در هر حالت، از نقطه اول به نقطه دوم ارسال کنید و زمان رسیدن پیغام به نقطه دوم را اندازه بگیرید. آیا امکان دارد زمان رسیدن پیغام در حالت اول، سریع‌تر از زمان رسیدن آن در حالت دوم باشد؟ گروهی از پژوهشگران، به این پرسش از دیدگاه نظری پاسخ داده‌اند. این گروه، برای پاسخ به این پرسش، به جای استفاده از معادله شرودینگر، از معادله دیراک استفاده کردند. بنابراین، به هیچ تضادی در ارتباط با نسبیت خاص اینشتین نرسیدند. این گروه آزمایشی را طراحی کردند. تصور کنید پیامی را به شکل مجموعه‌ای از ذرات رمز‌نگاری، و آن را به دوست خود می‌فرستید. از آنجا که بسیار عجله دارید، با خود فکر می‌کنید پیام را در خلأ بفرستید یا از طریق مانع. آیا تونل زنی کوانتومی می‌تواند این پیام را سریع‌تر برساند؟

پاسخ به پرسش بالا به این بستگی دارد که منظور شما از رسیدنِ پیام چیست. فرض کنید منظور از رسیدن پیام به فرد دوم همان رسیدن اولین ذره به او باشد. با در نظر گرفتن این فرض، پیام ارسال شده از طریق مانع، زودتر خواهد رسید. هرچه ضخامت مانع بزرگ‌تر باشد، تفاوت در زمان رسیدن پیام نیز بیشتر خواهد بود. بر طبق نتایج به‌دست آمده توسط این گروه پژوهشی، زمان متوسط سپری شده برای ذره‌های تونل‌زننده کوتاه‌تر از زمان متوسط سپری شده برای ذرات آزاد است. اما این نتیجه تنها در مورد ذره‌های گذرنده از مانع، صدق می‌کند. در واقع، بیشتر ذره‌های برخوردکننده با مانع، از آن منعکس می‌شوند. همچنین، هرچه ضخامت مانع بزرگ‌تر شود، ذرات بیشتری بازتابیده می‌شوند و در انتها، تنها تعداد کمی ذره عبور کرده‌اند.

سوال مهم آن است که آزمایش‌های تجربی در مورد زمان تونل زنی چه می‌گویند. آزمایش‌های انجام شده در اوایل دهه ۸۰ میلادی و پس از آن، اثر هارتمن را تایید کردند. اما تفسیر نتایج به‌دست آمده بسیار مشکل بود. همانند محاسبات نظری، تعریف زمان تونل زنی یا چگونگی اندازه‌گیری آن، مشکل اصلی بود. در آزمایش تجربی فیزیکی، به ساعت بسیار دقیقی نیاز است. در سال ۲۰۲۰، پژوهشی در این مورد در مجله nature چاپ شد. در این مقاله، از محور چرخشی اسپین ذره به عنوان ساعت استفاده شد. میدان مغناطیسی دو قطبی ذره، در میدان مغناطیسی خارجی می‌چرخد. از نرخ چرخش به عنوان ساعت داخلی استفاده می‌شود.

در این آزمایش، اتم‌های فوق سرد روبیدیم به میدان لیزری تابیده شدند. این میدان در ناحیه کوچکی گسترش یافته بود. این میدان به اندازه‌ای قوی بود که اتم‌های روبیدیم به طور کامل منحرف شدند. بنابراین، مانع غیر قابل‌عبوری ایجاد شد. گرچه، برخی از ذره‌ها از مانع عبور کردند. میدان مغناطیسی لیزر، اسپین این ذره‌ها را تغییر می‌داد و هرچه مدت زمان بیشتری داخل سد باقی می‌ماندند، اسپین آن‌ها بیشتر تغییر می‌کرد. اما چه چیزی از این آزمایش به‌دست آمد؟ آیا ذره‌ها سریع‌تر از سرعت نور حرکت کردند؟ خیر. این گروه پژوهشی در واقع به دنبال راهی برای استفاده از اسپین به عنوان ساعت داخلی بودند و موفق شدند.

تونل زنی کوانتومی به زبان ریاضی

تاکنون با مفهوم تونل زنی کوانتومی و کاربردهای مختلف آن در تکنولوژی آشنا شدیم. در این بخش، این مفهوم را به زبان ریاضی توضیح می‌دهیم. برای شروع کار، سد پتانسیلی همانند آنچه در مطالب بالا گفتیم را در نظر می‌گیریم. این حالت را می‌توان شبیه حالتی دانست که الکترون به هنگام حرکت در سیم با نقصی در آن روبرو می‌شود. اگر نقص موجود در سیم منجر به تولید پتانسیلی متفاوت با به بقیه سیم شود، سد پتانسیل ایجاد می‌شود.

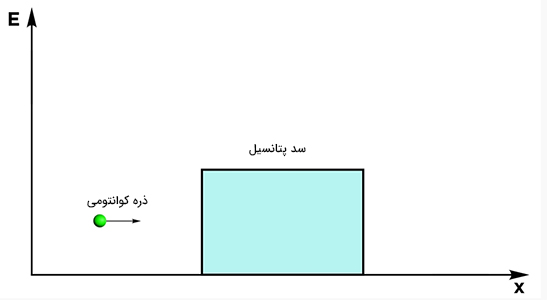
می‌دانیم که ذرات تمایل دارند در ناحیه‌هایی با پتانسیل کمتر قرار بگیرند. به عنوان مثال، اجسام به داخل نواحی با پتانسیل گرانشی کمتر سقوط می‌کنند. ذرات الکتریکی به سمت ناحیه‌هایی با پتانسیل الکتریکی کمتر، حرکت می‌کنند. فرض کنید ذره ابتدا در مکانی با پتانسیل صفر قرار دارد و انرژی آن برابر ۰/۵ است. سپس، ذره با سد پتانسیلی با ارتفاع یک برخورد می‌کند. اگر این مساله را در فیزیک کلاسیک بیان می‌کردیم، با قطعیت می‌دانستیم که ذره با این انرژی از سد پتانسیل عبور نمی‌کند و پس از برخورد با آن، در جهت مخالف منعکس می‌شود. اما مساله را در فیزیک کوانتوم مطرح کرده‌ایم. در فیزیک کوانتوم، بحث رفتار موجی-ذره‌ای ذره کوانتومی مطرح می‌شود.

برای تحلیل دقیق‌تر رفتار ذره کوانتومی به هنگام مواجه شدن با سد پتانسیل، معادله شرودینگر را حل می‌کنیم. برای راحتی کار، سیستم را یک‌بعدی در نظر می‌گیریم و معادله یک‌بعدی و مستقل از زمان شرودینگر را حل می‌کنیم:

$$- \ \frac{\hbar ^2}{2 m} \frac{\partial ^ 2 }{\partial x ^ 2} \psi (x) + V (x) \psi (x) = E \psi (x)$$

قبل از حل این معادله باید به این نکته توجه داشته باشیم که سیستم واقعی وابسته به زمان و سه‌بعدی است. گرچه، جواب‌های به‌دست آمده از معادله یک‌بعدی مستقل از زمان، تقریب خوبی برای سیستم واقعی خواهند بود. ارتفاع سد پتانسیل را برابر $$V_0$$ در نظر بگیرید. بنابراین، پتانسیل در تمام فضا به شکل زیر نوشته خواهد شد:

$$V(x) = \left\{V = 0 \ (0<x , \ x> a) , \ V = V_0 \ (0<x<a)\right\}$$

انرژی ذره کوانتومی یا کمتر از ارتفاع سد یا بیشتر از آن است. اگر کمتر باشد، به راحتی از سد می‌گذرد. اگر بیشتر باشد، پدیده تونل زنی کوانتومی رخ می‌دهد. گفتیم سد پتانسیل، فضا را به سه قسمت تقسیم می‌کند:

1. اگر $$x<0$$ باشد، مقدار پتانسیل برابر صفر است. این ناحیه را A می‌نامیم. ذره کوانتومی در این ناحیه به سد پتانسیل نزدیک می‌شود.
2. اگر $$x>a$$ باشد، مقدار پتانسیل برابر صفر است. این ناحیه را C می‌نامیم. این ناحیه بعد از سد پتانسیل قرار دارد.
3. اگر $$0$$ باشد، مقدار پتانسیل برابر $$V_0$$ است. این ناحیه را B می‌نامیم. ذره کوانتومی به داخل این ناحیه تونل می‌زند.

ابتدا، معادله شرودینگر را در قسمت‌های A و C حل می‌کنیم. مقدار انرژی پتانسیل، $$V$$، در این دو ناحیه برابر صفر است. بنابراین، در این دو ناحیه ذره آزادانه حرکت می‌کند و به عنوان ذره آزاد در نظر گرفته می‌شود. معادله شرودینگر در این دو ناحیه به شکل زیر نوشته می‌شود:

$$- \ \frac{\hbar ^2}{2 m} \frac{\partial ^ 2 }{\partial x ^ 2} \psi (x) = E \psi (x)$$

برای حل معادله فوق، دو طرف معادله را در $$- \ \frac {2m} { \hbar ^ 2}$$ ضرب می‌کنیم:

$$\frac{\partial ^ 2 }{\partial x ^ 2} \psi (x) = - \ \frac{2 m E}{\hbar ^ 2}E \psi (x)$$

کمیت $$k_0$$ را به صورت زیر تعریف می‌کنیم:

$$k _0 = \frac{\sqrt{2 m E}}{\hbar}$$

دو طرف معادله فوق را به توان دو می‌رسانیم:

$$k_0 = \frac{\sqrt{2 m E}}{\hbar}$$

با قرار دادن $$k_0 ^2$$ در معادله شرودینگر، داریم:

$$\frac{\partial ^2}{\partial x ^ 2} \psi (x) = - \ k_0 ^2 \psi ( x )$$

دو طرف معادله فوق را در یک سمت تساوی قرار می‌دهیم:

$$\frac{\partial ^2}{\partial x ^ 2} \psi (x) + \ k_0 ^2 \psi ( x ) = 0$$

به معادله دیفرانسیل درجه دوم می‌رسیم. این معادله را به طور مستقیم حل نمی‌کنیم، بلکه جواب‌های آن را حدس می‌زنیم و با قرار دادن در شرایط مرزی، آن‌ها را کامل حل می‌کنیم. دو شرایط مرزی برای این سد پتانسیل داریم.

1. شرط مرزی اول در $$x= 0$$
2. شرط مرزی دوم در $$x = a$$

تابع موج‌های دو ناحیه A و C را به صورت زیر حدس می‌زنیم:

$$\psi_A (x) = A e ^ {i k_0 x} + B e ^{ - \ i k_0 x}$$

(تابع موج ناحیه A)

$$\psi_C (x) = C e ^ {i k_0 x} + D e ^{ - \ i k_0 x}$$

(تابع موج ناحیه C)

در ادامه، معادله شرودینگر را در ناحیه B، داخل سد پتانسیل، در نظر می‌گیریم. در این ناحیه، انرژی پتانسیل برابر $$V_0$$ است.

$$$$- \ \frac{\hbar ^2}{2 m} \frac{\partial ^ 2 }{\partial x ^ 2} \psi (x) + V _ 0  \psi (x) = E \psi (x) $$$$

در این قسمت، باید به اندازه انرژی ذره کوانتومی توجه کنیم. اگر انرژی ذره کمتر از $$V_0$$ باشد، وجود ذره داخل انرژی پتانسیل غیرممکن به نظر می‌رسد. اما نباید رفتار دوگانه ذره را از یاد ببریم. هدف از نوشتن این معادلات و حل آن‌ها، پی بردن به شکل تابع موج ذره داخل سد پتانسیل است. تابع موج ذره داخل سد پتانسیل شبیه تابع موج ذره آزاد نخواهد بود. در نتیجه، نمی‌توانیم از تابع موج‌هایی شبیه $$\psi _A$$ یا $$\psi _ C$$ استفاده کرد. قبل از آن‌که شکل تابع موج در ناحیه B را حدس بزنیم، تفاوت دو تابع $$f_1 (x) = e^x + e ^ {-x}$$ و $$f_ 2 (x) = e^ {ix} + e ^ {- \ i k x}$$ را بیان می‌کنیم. تابع $$f _1 (x)$$ جمع دو تابع نمایی حقیقی و تابع $$f _ 2 (x)$$ جمع دو تابع نمایی مختلط هستند. به شکل هر یک از این دو تابع توجه کنید.

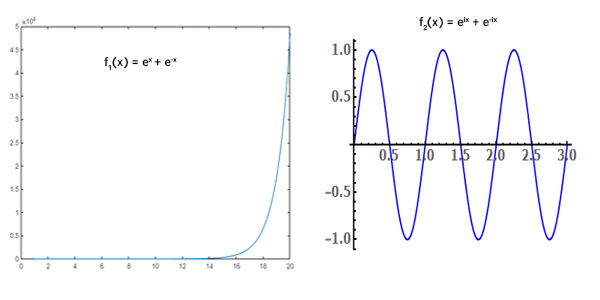
تابع $$f_2 (x)$$ همان تابع موج برای ذره آزاد است. تابع موج ذره کوانتومی در صورت عدم وجود سد پتانسیل، همانند تابع $$f_2 (x)$$ خواهد بود. در مقابل، تابع $$f_1 (x)$$ تابعی محلی است. این تابع، ناحیه باریکی را اشغال می‌کند و به سرعت متوقف می‌شود. از این تابع در ناحیه B، استفاده می‌شود. در واقع، این تابع بیان‌گر شکل ریاضی سد پتانسیل است. ذره کوانتومی با احتمال کمی به سد پتانسیل وارد می‌شود.

1. اگر انرژی ذره کمتر از ارتفاع سد پتانسیل باشد، جواب معادله شرودینگر تابع نمایی حقیقی است.
2. اگر انرژی ذره بیشتر از ارتفاع سد پتانسیل باشد، جواب معادله شرودینگر تابع نمایی مختلط است.

انرژی ذره کمتر از ارتفاع سد پتانسیل است

در این حالت، معادله شرودینگر به صورت زیر نوشته می‌شود:

$$- \ \frac{\hbar ^2}{2 m} \frac{\partial ^ 2 }{\partial x ^ 2} \psi (x) + V _ 0 \psi (x) = E \psi (x)$$

$$E \psi (x)$$ را به سمت چپ معادله می‌آوریم:

$$- \ \frac{\hbar ^2}{2 m} \frac{\partial ^ 2 }{\partial x ^ 2} \psi (x) + V _ 0 \psi (x) - E \psi (x) = 0$$

$$V _ 0 \psi (x) - E \psi (x)$$ به صورت یک جمله می‌نویسیم:

$$- \ \frac{\hbar ^2}{2 m} \frac{\partial ^ 2 }{\partial x ^ 2} \psi (x) + (V _ 0 - E) \psi (x) = 0$$

کاری که باید از اینجا به بعد انجام دهیم، شبیه حل معادله شرودینگر برای ذره آزاد است. ابتدا طرفین معادله فوق را در $$\ \frac {2m} { \hbar ^ 2}$$ ضرب می‌کنیم:

$$- \ \frac{\partial ^ 2 }{\partial x ^ 2} \psi (x) + \frac{2 m}{\hbar^ 2} (V _ 0 - E) \psi (x) = 0$$

کمیتی به نام $$k_{below}$$ به صورت زیر تعریف می‌کنیم:

$$k_{below} = \frac{\sqrt{2 m ( V_0 - E)}}{\hbar}$$

نام below برای آن انتخاب شده است که انرژی ذره کوانتومی کمتر از ارتفاع سد پتانسیل است. با قرار دادن $$k_{below}$$ در معادله شرودینگر، آن را به صورت زیر می‌نویسیم:

$$- \ \frac{\partial ^ 2 }{\partial x ^ 2} \psi (x) + k_{below} ^ 2 \psi (x) = 0$$

معادله شرودینگر به شکل معادله دیفرانسیل درجه دو درآمده و شبیه معادله ذره آزاد است. در این حالت، جواب معادله را می‌توان به صورت جمع خطی دو تابع نمایی حقیقی نوشت.

$$psi ( x) _ {below} = F e ^ {k_{below} x} + G e ^ {- k_ {below} x}$$

ذره در ناحیه B نمی‌تواند آزادانه حرکت کند، بنابراین تابع موج را به این صورت می‌نویسیم.

انرژی ذره بیشتر از ارتفاع سد پتانسیل است

این حالت بسیار شبیه حالت اول است، با این تفاوت که ثابت دیگری باید تعریف شود:

$$k_{above} = \frac{\sqrt{ 2 m ( E - V_0)}}{\hbar }$$

$$k_{above}$$ مشابه $$k_{below}$$ است، با این تفاوت که $$V_0 - E$$ fh با $$E - V _ 0$$ جایگزین می‌شود.

$$- \ \frac{\partial ^ 2 }{\partial x ^ 2} \psi (x) + k_{above} ^ 2 \psi (x) = 0$$

هنگامی که انرژی ذره از ارتفاع سد پتانسیل بیشتر باشد، تابع موج ناحیه B نیز شبیه تابع موج ناحیه‌های A و C است. زیرا ذره می‌تواند در این ناحیه نیز همانند دو ناحیه دیگر آزادانه حرکت کند و وجود سد پتانسیل تاثیری روی حرکت آن نخواهد گذاشت. جواب این معادله را به صورت زیر می‌نویسیم:

$$\psi ( x) _ {above} = H e ^ {i k_{above} x} + K e ^ {- i k_ {below} x}$$

در ادامه، تابع موج‌های نوشته شده برای هر بخش را به دو قسمت تقسیم می‌کنیم. به عنوان مثال، تابع موج نوشته شده برای ناحیه A به دو قسمت $$\psi _ {right, A} ( x) = A e ^ {ik_0 x}$$ و $$\psi _ {left, A} ( x) = B e ^ {ik_0 x}$$ تقسیم می‌شود. $$\psi _ {right, A} ( x) = A e ^ {ik_0 x}$$ و $$\psi _ {left, A} ( x) = B e ^ {ik_0 x}$$، به ترتیب قسمتی از تابع موجِ مربوط به حرکت ذره به سمت راست یا چپ در ناحیه A است. همچنین، ضریب‌های A و B نشان‌دهنده احتمال نسبی حرکت ذره به سمت راست یا چپ هستند.

تابع موج در ناحیه C را نیز به طور مشابه می‌توان به دو قسمت تقسیم کرد:

$$\psi _ {right, C} ( x) = C e ^ {ik_0 x}$$

$$\psi _ {left, C} ( x) = D e ^ {ik_0 x}$$

تابع موج در ناحیه B به دو صورت نوشته می‌شود:

1. اگر انرژی ذره از ارتفاع سد پتانسیل بیشتر باشد، تابع موج آن در ناحیه B به شکل $$\psi ( x) _ {above} = H e ^ {i k_{above} x} + K e ^ {- i k_ {below} x}$$ نوشته می‌شود. در این حالت، تابع موج را می‌توان به دو قسمت $$\psi _ {B, above, right} ( x) = H e ^ {ik_{above} x}$$ و $$\psi _ {B, above, left} ( x) = K e ^ {ik_{above} x}$$ تقسیم کرد.
2. اگر انرژی ذره از ارتفاع سد پتانسیل کمتر باشد، تابع موج آن در ناحیه B به شکل $$psi ( x) _ {below} = F e ^ {k_{below} x} + G e ^ {- k_ {below} x}$$ نوشته می‌شود. در این حالت، تابع موج را نمی‌توان به دو بخش راست و چپ تقسیم کرد، زیرا تابع موج در این حالت به صورت ترکیب خطی تابع نمایی حقیقی نوشته می‌شود و نشان‌دهنده موج رونده نیست. به بیان دیگر، ذره آزاد نیست و در ناحیه کوچکی از فضا محبوس می‌شود.

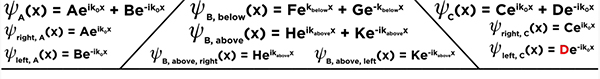
اکنون، همه چیز برای یافتن توابع موج هر ناحیه آماده است. فرض کنید ذره‌ای از سمت چپ به سد پتانسیل نزدیک می‌شود. با این فرض، ثابت D را می‌توان برابر صفر قرار داد. در واقع، هیچ موجی از سمت راست به سد پتانسیل نزدیک نمی‌شود. بنابراین $$\psi _ {left , C}$$ برابر صفر خواهد بود. ثابت‌های دیگر، مانند A و B، مقدار دارند. زیرا حرکت ذره به سمت راست در ناحیه‌های A و B و C نشان‌دهنده آن است که ذره به داخل سد نفوذ کرده است و با احتمال کمی در طرف دیگر سد یافت می‌شود.

حرکت ذره به سمت چپ در ناحیه A تنها در صورتی ممکن است که قسمتی از موج آن در برخورد به سد، منعکس شده باشد. اگر ذره به داخل سد نفوذ کند، حرکت به سمت چپ نیز در ناحیه B ممکن خواهد بود. بنابراین حرکت به سمت راست در ناحیه C تنها حرکتی است که انجام نمی‌گیرد.

اکنون ذره‌ای را در نظر بگیرید که انرژی آن کمتر از $$V _ 0$$ است. با استفاده از شرایط مرزی، ثابت‌ها را به‌دست می‌آوریم. دنبال شرایط مرزی هستیم که تابع موج و مشتق آن در آنجا پیوسته باشند. همچنین، تابع موج باید بهنجار باشد.

$$\int_{- \infty}^{\infty} \psi ^* ( x) \psi ( x ) \ dx = 1$$

در ابتدا، مرز $$x = 0$$ را بررسی می‌کنیم. این مرز بین دو ناحیه A و B قرار گرفته است. بنابراین در این ناحیه باید:

$$\psi _ A = \psi _ {B, below}$$

تساوی بالا نشان می‌دهد که تابع موج به هنگام عبور از $$x = 0$$، پیوسته است. عبارت‌های مربوط به تابع موج در ناحیه A و B را در رابطه فوق قرار می‌دهیم:

$$‌A e ^ {i k_0 x} + ‌B e ^ {- i k_0 x} = F e ^ {k_{below} x} + G e ^ {- k_{below} x}$$

در رابطه فوق، $$x$$ را برابر صفر قرار می‌دهیم و به رابطه زیر می‌رسیم:

$$A + B = F + G$$

همچنین، گفتیم مشتق تابع موج نیز باید در مرز پیوسته باشد:

$$\frac{\partial }{\partial x} \psi _ A = \frac{\partial }{\partial x} \psi _ {B, below}$$

$$‌\frac{\partial }{\partial x} (A e ^ {i k_0 x} + ‌B e ^ {- i k_0 x}) = \frac{\partial }{\partial x} (F e ^ {k_{below} x} + G e ^ {- k_{below} x} )$$

با گرفتن مشتق از رابطه فوق و قرار دادن $$x = 0$$ در آن، داریم:

$$\\ i k_0 A - i k_0 B = k_{below} F - k _ {below} G$$

در ادامه، مرز دوم، یعنی $$x = a$$، را در نظر می‌گیریم:

$$\psi_{B, below} = \psi _ {C}$$

$$Fe ^ {k_{below} x} + G e ^ {- k_{below} x} = C e^ {i k_ 0 x} + D e ^ { - i k_0 x}$$

از آنجا که ضریب D برابر صفر است، رابطه فوق به صورت زیر نوشته می‌شود:

$$Fe ^ {k_{below} x} + G e ^ {- k_{below} x} = C e^ {i k_ 0 x}$$

سپس، به جای x در معادله فوق، a قرار می‌دهیم:

$$Fe ^ {k_{below} a} + G e ^ {- k_{below} a} = C e^ {i k_ 0 a}$$

پیوستگی مشتق توابع موج در ناحیه‌های B و C را نیز در $$x = a$$ بررسی می‌کنیم.

$$\frac{\partial }{\partial x} (Fe ^ {k_{below} x} + G e ^ {- k_{below} x}) = \frac{\partial }{\partial x} (C e^ {i k_ 0 x} ) \\ k_{below} F e ^ {k_{below} a} - k_{below} G e ^ {- k_{below} a}= i k_0 C e ^ {i k_0 a}$$

بنابراین، با نوشتن شرایط مرزی برای توابع موج و مشتق‌های آن‌ها، به چهار معادله می‌رسیم. نکته مهم آن است که چهار معادله، اما پنج مجهول داریم. به‌دست آوردن این مجهول‌ها مهم نیستند، بلکه نسبت آن‌ها به یکدیگر، که به ما ضریب عبور و ضریب بازتاب را می‌دهند، مهم هستند.

تاریخچه تونل زنی کوانتومی

این پدیده، نخستین بار توسط فیزیک‌دانی به نام «هوند» (Hund) در سال ۱۹۲۷، به هنگام محاسبه انرژی حالت پایه، مشاهده شد. در همان سال، این پدیده توسط فیزیک‌دان دیگری به نام «نورهیم» (Nordheim) به هنگام مطالعه بازتاب الکترون‌ها از سطوح مختلف، مشاهده شد. چند سال بعد، اوپنهایمر با استفاده از از تونل زنی، نرخ یونش هیدروژن را به‌دست آورد.

جمع بندی

در این مطلب، در مورد تونل زنی کوانتومی و کاربردهای مختلف آن در صنعت الکترونیک و طبیعت صحبت کردیم. تونل زنی از سد پتانسیل در فیزیک کلاسیک هیچ معنایی ندارد، اما در دنیای عجیب کوانتوم، این پدیده اتفاق می‌افتد. اصل عدم قطعیت هایزنبرگ و رفتار موجی-ذره‌ای ذره کوانتومی دلیل‌های اصلی تونل زنی کوانتومی هستند.