درهم تنیدگی کوانتومی — به زبان ساده
امروزه کوانتوم به خصوص مباحث ویژهای از آن نظیر رمزنگاری و کامپیوترهای کوانتومی به بحث داغ دنیای فیزیک و تکنولوژی تبدیل شده است. در این مقاله سعی داریم تا با مفهوم «درهم تنیدگی کوانتومی» (Quantum Entanglement) به طور خیلی ساده و به دور از روابط ریاضی بپردازیم.
در یک جمله درهم تنیدگی کوانتومی را میتوان همبستگی ذرات تعریف کرد. آلبرت انیشتین درهمتنیدگی را «رفتار عجیب در فاصلهی دور» (Spooky Action at a Distance) نامید. جدا از کاربرد در همتنیدگی در تحقق یافتن فیزیکی کامپیوترهای کوانتومی، فهم و چگونگی بهرهوری از پدیده درهم تنیدگی کوانتومی در دیگر رخدادهای فیزیکی جالب توجه است. برای مثال، با استفاده از پدیده درهمتنیدگی میتوان اندازهگیری دقیقی از امواج گرانشی یا درک بهتری نسبت به خصوصیات مواد با خصوصیات عجیب (Exotic) داشت. برای اینکه با مفهوم پدیده درهمتنیدگی و رفتار شبهوار ذرات آشنا شوید با ما در ادامه این مقاله همراه باشید تا این مفهوم را از دو منظر قوانین پایستگی و «برهمنهی» (Superposition) کوانتومی بررسی کنیم.
قوانین پایستگی
قوانین پایستگی از قوانین فراگیر و عمیق علم فیزیک است. به طور مثال قانون پایستگی انرژی بیان میکند که انرژی کل یک سیستم ایزوله ثابت باقی میماند، هر چند که به فرمهای مختلف انرژی (گرمایی، مکانیکی و الکتریکی) تبدیل شود. همچنین یک سیستم میتواند مقداری انرژی با محیط اطراف خود مبادله کند، اما به هر حال مقدار کلی انرژی همیشه ثابت است.
آیا دقت کردهاید که چرا وقتی دو اسکیتباز بر روی یخ با وزن های مختلف یکدیگر را هل می دهند، شخصی که وزن کمتری دارد سریعتر از شخص دیگر حرکت می کند؟! جواب این سوال را میتوان در قانون پایستگی تکانه جستوجو کرد. اساس کار این قانون همان عبارت معروف «هر عملی عکسالعملی برابر در خلاف جهت دارد» یا قانون سوم نیوتن است. بار دیگر اسکیتباز روی یخ را تجسم کنید. دلیل چرخش سریعتر به دور خود، وقتی دستهایش را در نزدیکی خودش قرار می دهد، در قانون پایستگی تکانه زاویهای نهفته است.
قوانین پایستگی، به طور تجربی نیز اثبات و در همه جای جهان از بزرگترین مقیاسها مثل سیاهچالهها تا مقیاسهای خیلی کوچک مثل رفتار الکترون در اتمها به کار میروند.
جمع کوانتومی
تصور کنید که در یک جنگل در حال پیادهروی هستید و روبهروی خود یک دو راهی میبینید. سمت چپ محیطی ترسناک و تاریک و سمت راست محیطی زیبا و پر نور است. احتمال خیلی زیاد شما تصمیم میگیرید از مسیر سمت راست به راه خود ادامه دهید. اما اگر شما در دنیای کوانتومی زندگی میکردید میتوانستید هر دو مسیر را به طور همزمان انتخاب کنید!

برای سیستمی که توسط قوانین مکانیک کوانتومی شرح داده میشود، البته سیستمی که از نویز و تاثیرات محیط بیرون در امان و ایزوله باشد، با قوانین جذاب و شاید عجیبی روبهرو هستیم. به طور مثال برای اسپین یک الکترون نمیتوان به طور صریح اشاره کرد که اسپین آن به سمت بالا یا پایین است. اما عبارت درستتر از نقطه نظر قوانین مکانیک کوانتومی این است که بگوییم حالت اسپین الکترون به صورت بالا + پایین است.
حالتهای یک سیستم کوانتومی میتواند با هم جمع یا از هم جدا شوند. از لحاظ ریاضی، قوانین جدایی یا ترکیب حالات کوانتومی یک سیستم از قوانین جمع و تفریق برداری پیروی میکنند. لازم به ذکر است که حالت یک سیستم کوانتومی که آن را با نماد «کت» $$(|\rangle)$$ نمایش میدهند، در واقع یک بردار در فضای هیلبرت است. در فیزیک کوانتوم، کلمهای که به ترکیب شدن حالات کوانتومی اطلاق میکنند، برهمنهی (Superposition) است.
نکته مورد توجه این است که قبل از انجام عمل اندازهگیری به طور دقیق نمیتوان گفت که سیستم در کدام یک از حالات برهمنهی است. به طور مثال شما نمیتوانید الکترون را مجبور کنید در لحظهای که انتظار دارید اسپین بالا داشته باشد. بلکه الکترون در هر لحظه و در آن واحد میتواند در هر دو حالت اسپین بالا و پایین حضور داشته باشد و شما فقط با انجام عمل اندازهگیری میتوانید حالت اسپین آن را مشخص کنید. مثال دیگر همان گربه معروف شرودینگر است که تا ما در جعبه را باز نکنیم (باز کردن در جعبه مصداق اندازهگیری است) نمی توانیم مطمئن شویم که گربه زنده یا مرده است.

درهم تنیدگی کوانتومی و قانون پایستگی
درهم تنیدگی کوانتومی به این معنا است که نظریه کوانتوم نیازمند جهانهای بسیاری است. اجازه دهید دو مبحث فوق را باهم به کار برده و قانون پایستگی انرژی را به دو سیستم جفت شده کوانتومی اعمال کنیم البته با علم به این موضوع که درهم تنیدگی کوانتومی تفاوت اصلی بین فیزیک کلاسیک و کوانتوم است و چیزی به نام درهم تنیدگی در فیزیک کلاسیک وجود ندارد اما این مثال برای فهم بیشتر مفهوم درهم تنیدگی است.
تصور کنید دو جفت ذرات کوانتومی (به طور مثال اتمها) با مجموع انرژی ۱۰۰ واحد در اختیار دارید. شما به همراه دوست خود شروع به جدا کردن ذرات جفت شده میکنید. در انتهای کار شما میبینید که ذراتی با 40 واحد انرژی دارید. با استفاده از قانون پایستگی انرژی میتوان گفت که دوست شما ذراتی با تعداد 60 واحد انرژی در اختیار دارد. حتی اگر دوست شما هیچ اطلاعاتی از مقدار واحدهای انرژی که در دست دارد را به شما مخابره نکند، یا حتی دوست شما در آن طرف دیگر کهکشان باشد، شما با اندازهگیری انرژي اتمهای خود و به وسیله قانون پایستگی انرژی می توانید از تعداد واحدهای انرژی که وی در دست دارد، مطلع شوید.
حالات یک سیستم کوانتومی مانند اتمها در مثال فوق میتواند جالبتر نیز باشد. در این مثال، انرژی ذرات جفت شده را میتوان با حفظ انرژی کل (قانون پایستگی انرژی) به صورت جمع حالتهای مختلفی نوشت. به طور مثال:
[اتمهای شما 60؛ اتمهای دوست شما 40] + [اتمهای شما 30؛ اتمهای دوست شما 70] + ....
تعابیر فوق بر اساس پایستگی انرژی بیان شده است. در واقع قبل از اندازهگیری، به طور دقیق نمیتوان گفت مجموعه اتمهای شما و مجموعه اتمهای دوست شما کدام یک از حالات برهمنهی فوق است. اما با این حال، با توجه به قانون پایستگی انرژی چیزی که واضح است مجموع انرژی 100 واحدی سیستم است. خواص دو جفت اتمهایی که در اختیار شما و دوست شما است با توجه به قانون پایستگی انرژی همبسته میماند (مجموع انرژی دو جفت ذرات باید به مقدار 100 واحد باشد).
به طور مثال اگر شما با اندازهگیری روی سیستم خود (مجموعه اتمها) متوجه شوید که مقدار 70 واحد انرژی در اختیار دارید، بلافاصله میتوانید متوجه شوید که دوست شما مجموعه ذراتی با 30 واحد انرژی را در اختیار دارد. در حقیقت میتوان به نوعی مفهوم بین درهم تنیدگی را با پایستگی انرژی تعریف کرد. یعنی اگر شما اندازه انرژی کل یک سیستم را بدانید و انرژی یک سیستم را اندازهگیری کنید نسبت به انرژی سیستم دوم نیز اطلاعاتی به دست میآورید.
به عنوان مثالی دیگر از درهم تنیدگی کوانتومی جسمی به نام $$c$$ را در نظر بگیرید که میتواند در دو حالت دایرهای و مربعی موجود باشد. در نتیجه از ترکیب دو $$c$$ چهار حالت ممکن است اتفاق بیفتد: (مربع، مربع)، (دایره، دایره)، (مربع، دایره) و (دایره، مربع) که احتمال رخداد هر یک از این حالتها $$25\%$$ است. این حالتها را حالتهای مستقل میگوییم.
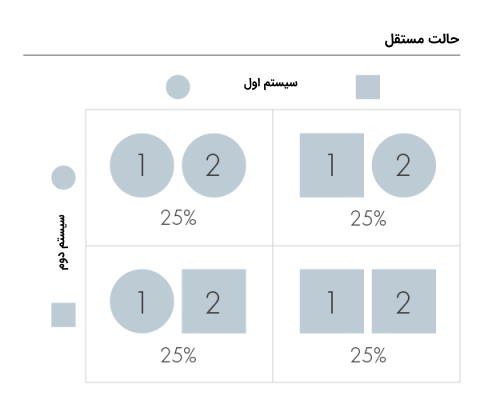
در تصویر بالا حالتها را مستقل در نظر میگیریم زیرا دانش ما در مورد یک حالت، اطلاعاتی در مورد حالت دوم ارائه نمیدهد. یعنی اگر ما بدانیم $$c$$ ابتدایی در حالت مربعی است هنوز در مورد حالت $$c$$ دوم در جهل و بیدانشی به سر میبریم. اما در صورتی که حالتها درهم تنیدگی داشته باشند موضوع کاملاً متفاوت خواهد بود.
در حالت درهم تنیده اگر $$c$$ اول دایرهای باشد، $$c$$ دوم نیز باید شکل دایرهای داشته باشد و اگر مربعی باشد حالت دوم نیز به همین صورت است. در حقیقت تعداد حالتها به دو حالت کاهش مییابد و داریم: (مربع، مربع)، (دایره، دایره).
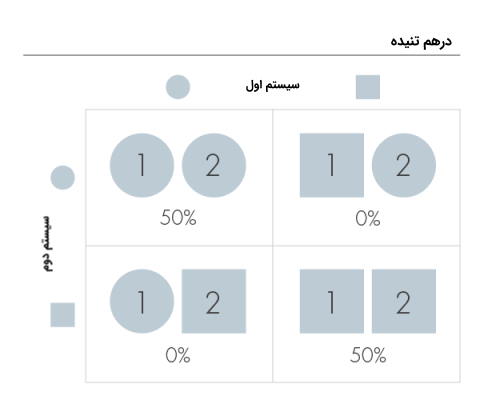
طبق تصویر بالا در حالت درهم تنیده احتمال وقوع حالت دایرهای $$50\%$$ و احتمال وقوع حالت مربعی نیز $$50\%$$ است و با علم از شکل یکی از $$c$$ها شکل یا اطلاعات در مورد حالت دوم نیز به دست میآوریم.
ورژن کوانتومی درهم تنیدگی به همین معنی است، یعنی در حالتهای کوانتومی کمبود استقلال وجود دارد و حالتهای کوانتومی به هم تنیده یا وابسته هستند. تفاوت در این است که در فیزیک کوانتوم حالتها با ابزارهای ریاضی که به آنها تابع موج میگوییم تعریف میشوند.
اگر بخواهیم مثال بالا را به صورت توابع موجی $$\psi_{\blacksquare}$$ و $$\psi_{\bullet}$$ برای حالت اول و $$\Phi_{\blacksquare}$$ و $$\Phi_{\bullet}$$ برای حالت دوم بنویسیم برای حالت مستقل و درهم تنیده داریم:
$$\text { Independent: } \Phi_{\blacksquare} \psi_{\blacksquare}+\Phi_{\blacksquare} \psi_{\bullet}+\Phi_{\bullet}\psi_{\blacksquare}+\Phi_{\bullet} \psi_{\bullet}$$
$$\text { Entangled: } \Phi_{\blacksquare} \psi_{\blacksquare}+\Phi_{\bullet} \psi_{\bullet}$$
یکی از نتایج بارز درهم تنیدگی در نظریه کوانتوم «اصل متممیت» (complementarity) است که آن را در ادامه توضیح میدهیم. برای توضیح اصل متممیت فرض کنید که اگر به حالت $$c$$ غیر از شکل هندسی ویژگی تحت عنوان رنگ نیز اضافه کنیم در نتیجه حالتهای ممکن برای $$c$$ به صورت (دایره قرمز)، (مربع قرمز)، (مربع آبی) و (دایره آبی) خواهد بود. در این حالت ما میتوانیم اطلاعاتی در مورد شکل $$c$$ به دست بیاوریم اما در این حالت تمام اطلاعات ما در مورد رنگ این حالت از بین میرود و براساس نظریه کوانتوم نمیتوانیم شکل و رنگ این حالت را به طور همزمان اندازهگیری کنیم.
بر این اساس هیچ نظریهای به طور کامل و مطلق تمام جنبههای فیزیکی یک حالت را ارائه نمیدهد و باید دیدگاههای مختلف و منحصر به فردی را در نظر گرفت که هرکدام بینشی معتبر اما جزئی پیش روی ما قرار میدهند این همان چیزی است که نیلز بور آن را به صورت ریاضی بیان کرد و به عنوان اصل متممیت شناخته میشود.
درهم تنیدگی کوانتومی به چه معنا است؟
درهم تنیدگی کوانتومی یک پدیده فیزیکی است و هنگامی اتفاق میافتد که یک جفت یا گروهی از ذرات به وجود آمده که با یکدیگر برهم کنش داشته یا فضای هندسی را با هم اشغال کنند به گونهای هستند که حالت کوانتومی هر ذره از جفت یا گروه را نتوان مستقل از حالت ذره دیگر توصیف کرد. این ویژگی حتی زمانی که ذرات با فاصله زیادی از هم جدا میشوند نیز وجود دارد. مبحث درهم تنیدگی کوانتومی در حقیقت تفاوت اصلی بین فیزیک کلاسیک و فیزیک کوانتوم است و باید گفت درهم تنیدگی ویژگی اصلی مکانیک کوانتوم است که در مکانیک کلاسیک وجود ندارد.
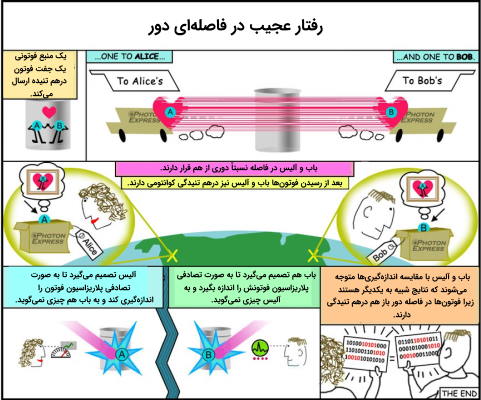
آلبرت اینشتین، بوریس پودولسکی و ناتان روزن (EPR) شرایطی که دو حالت به یکدیگر به صورت کوانتومی درهم تنیده هستند اینگونه توضیح دادند که اگر یک جفت EPR (EPR ابتدای اسامی اینشتین، پودولسکی و روزن است) شامل دو $$q$$ باشند هر یک از آنها را میتوان از لحاظ شکل و رنگ (اما نه هر دو ویژگی) اندازهگیری کرد. در این اندازهگیری اگر ما شکل یکی از جفتهای EPR را اندازهگیری کنیم درمییابیم که با احتمال یکسان میتوانند به شکل دایرهای یا مربع باشد و اگر رنگ آن را اندازهگیری کنیم میبینیم که با احتمال یکسان میتواند قرمز یا آبی باشند.

پارادوکسی که اندازهگیری EPR ایجاد میکند مربوط به زمانی است که اندازهگیری را بر روی هر دو حالت انجام دهیم. هنگامی که هر دو عضو را از نظر رنگ یا از لحاظ شکل هندسی اندازه میگیریم متوجه میشویم که نتایج همیشه مشابه یکدیگر هستند یعنی اگر در فرآیند اندازهگیری متوجه شویم که رنگ یکی از حالتها قرمز است و بعد رنگ حالت دیگر را اندازه گیری کنیم متوجه خواهیم شد که رنگ آن نیز قرمز است. همچنین اگر در اندازهگیری متوجه شویم که شکل یکی از حالتها مربع است و سپس شکل هندسی حالت دوم را اندازهگیری کنیم میبینیم که شکل حالت دوم نیز مربع است.
این در حالی است که اگر رنگ یکی از حالتها و شکل حالت دیگر را اندازهگیری کنیم متوجه میشویم که هیچ ارتباطی بین این دو اندازهگیری وجود ندارد.
طبق تئوری کوانتوم حتی اگر فاصله بین این دو اندازهگیری زیاد بوده و این دو سیستم کاملاً از هم جدا باشند و اندازهگیریها تقریباً همزمان انجام شود نتایج و مشاهدات یکسان است و مانند حالتی است که دو سیستم نزدیک هم بودهاند. در حقیقت به نظر میرسد انتخاب نوع کمیتی که مورد اندازهگیری قرار میگیرد در یک مکان بر وضعیت سیستم درهم تنیده در مکان دیگر تأثیر میگذارد. این اتفاق خارقالعاده و شبحوار در یک فاصله نسبتاً دور، تعبیری که انیشتین به کار برد، به نظر میرسد که به انتقال اطلاعات نیاز دارد و این اطلاعات باید با سرعتی منتقل شود. اما آیا سرعت انتقال این دادهها بیشتر از سرعت نور است؟
با تأمل عمیقتر این پارادوکس بیشتر حل میشود. دوباره سیستم دو حالتی را با توجه به اینکه سیستم اول قرمز اندازهگیری شده است در نظر بگیرید و بر روی سیستم دوم تمرکز کنید. اگر بخواهیم رنگ سیستم دوم را اندازه بگیریم مطمئناً قرمز خواهد بود. اما همانطور که قبلاً در هنگام توضیح اصل متممیت گفتیم، اگر اندازهگیری شکل سیستم دوم را در حالتی که میدانیم قرمز است انتخاب کنیم احتمال یافتن یک مربع یا یک دایره به صورت مساوی خواهد بود.
مثال نهایی از درهم تنیدگی را به این صورت توضیح میدهیم که اگر هر یک از جفتهای یک دستکش را درون جعبههای جداگانهای قرار دهیم و آنها را به طرف شرق و غرب کره زمین پرتاب کنیم، تعجب آور نخواهد بود که با نگاه کردن به داخل یکی از جعبهها بتوانید راست بودن یا چپ بودن جفت دیگر دستکش را تعیین کنید. به همین ترتیب در همه موارد شناخته شده همبستگی و درهم تنیدگی بین یک جفت EPR باید زمانی که اعضای آن به هم نزدیک هستند رخ داده باشد و بدین ترتیب این حالتها میتوانند بعد از جدایی نجات پیدا کنند زیرا حافظه آنها دادهها را ثبت کرده است. در حقیقت این حالتها مکمل یکدیگر هستند.
سرعت انتقال دادهها در اندازهگیری سیستمهایی که درهم تنیدگی کوانتومی دارند چه قدر است؟
تا زمانی که فردی از نتیجهای که شما کسب کردهاید مطلع نشود نمیداند که باید انتظار چه چیزی را داشته باشد. در حقیقت اطلاعات مفید زمانی به شخص منتقل میشود که از نتایج اندازهگیری شما مطلع شود و این امر در لحظهای که شما اندازهگیری را انجام میدهید رخ نمیدهد و زمانی اتفاق میافتد که نتایج را به او اعلام کنید یا خودش آنها را ببیند. در حقیقت هر پیامی که نتیجه اندازهگیری شما را فاش میکند باید به روش فیزیکی مشخصی به شخص دیگر منتقل شود و این سرعت انتقال احتمالاً کندتر از سرعت نور است.

با این حال آزمایشات و بررسیهای اخیر نشان میدهد که سرعت انتقال دادهها در درهم تنیدگی کوانتومی بیشتر از سرعت نور است که مقدار آن به عنوان یکی از مهمترین اصلهای نسبیت شناخته میشود.
در صورت علاقهمندی به مباحث مرتبط در زمینه فیزیک، آموزشهای زیر نیز به شما پیشنهاد میشوند:











بسیار روان و عالی توضیح داده شد مبحثی که تا به حال نفهمیده بودم از منابع- ممنون از زحمات
سلام.در پاسخ به سوال علیرضا چیزی که میتوانم بگویم این است همین چیزی که شما قبول کردی در مورد فروپاشی نتیجه آزمایشاتیست که در فواصل مختلف بین دو ذره درهمتنیده انجام شده.که در نهایت برای ثبت نتیجه هر آزمایش در فواصل مختلف نیاز به مخابره نتیجه اندازه گیری مشاهده گرها در دو نقطه مورد نظر است.
با سلام. آنچه من ميخواستم بدانم اينست که منشاء درهم تنيدگي کوانتومي چه زماني و توسط چه کسي مطرح شد
درباره اینکه هنوز انتقال اطلاعات در حیطه سرعت نور هست متوجه نشدم. مگر نه اینکه دو ذره درهم تنیده در دو طرف کهکشان با یک میلون سال نوری فاصله هستند و افرادی نیز جدا گانه و بی خبر از هم این ذرات رو مبینن. خب فروپاشی تابع موج ذره اول بلافاصله باعث فروپاشی ذره دوم میشه و شخصی که ذره دوم رو مشاهده میکنه میفهمه که تابع موج ذره اول هم فروپاشیده شده و شامل این خصوصیات هست بدون انتقال داده در یک ملیون سال نوری. پس چطور سرعت انتقال داده همچنان در حیطه سرعت نور هست؟
سلام در هم تنیدگی کوانتومی خیلی خیلی هیجان انگیز هست ممنونم از این آموزش خوب و بیان ساده من کاملا یاد گرفتم?✌