چاه پتانسیل (Potential Well) یا ذره در جعبه — به زبان ساده

در مکانیک کوانتومی، مسئله ذره در جعبه که به «چاه پتانسیل بی‌نهایت» (Infinite Potential Well) نیز معروف است، بیانگر وضعیت ذره آزادی بوده که در یک فضای کوچک غیر قابل نفوذ به دام افتاده، در آن حرکت می‌کند و توانایی خارج شدن از آن را ندارد. این مسئله در واقع مثالی شهودی برای درک بهتر تفاوت دو دیدگاه فیزیک کلاسیک و مکانیک کوانتومی است.

در فیزیک و مکانیک کلاسیک، ذره به دام افتاده در جعبه‌ای بزرگ، می‌تواند هر سرعتی را اختیار کند و در حالت خیلی ساده تنها یک مسیر را طی می‌کند تا انرژیش تمام شود. با کوچک شدن ابعاد جعبه تا مقیاس‌ چند نانومتر، رفتارهای کوانتومی نمود بیشتری پیدا می‌کنند. در این حالت، ذره فقط می‌تواند برخی از سطوح انرژی مثبت را اختیار و در آن سطح‌ها حرکت کند. بدین ترتیب هیچگاه نمی‌تواند انرژی صفر را داشته باشد (تراز انرژی صفر وجود ندارد) و لذا هیچگاه نمی‌تواند به حالت سکون در آید.

همچنین در حالت کوانتومی، احتمال یافتن ذره بستگی به تابع توزیع دارد که خود وابسته به ترازهای انرژی است. از طرفی ذره ممکن است در نقاط خاصی موسوم به گره فضایی، هیچگاه یافت نشود.

مسئله ذره در جعبه، یکی از مسائل مکانیک کوانتومی است که بدون نیاز به روابط پیچیده ریاضی و به صورت تحلیلی حل می‌شود. این مسئله که اساس آن، بحث کوانتیده (گسسته) بودن ترازهای انرژی است، درک مناسبی در برخورد با مسائل پیچیده‌تر و تشریح سیستم‌های اتمی و مولکولی به ما می‌دهد. با ما در ادامه این مقاله همراه باشید تا به زبانی ساده مفاهیم و روابط مربوط به‌ آن را بیان کنیم. در ابتدای امر، برای اینکه درک بهتری از مسئله داشته باشیم، به تشریح مدل یک بعدی می‌پردازیم. در انتها نیز مدل دو و سه بعدی که در واقع تعمیمی از حالت یک بعدی هستند، عنوان می‌شوند.

ذره در جعبه (چاه پتانسیل) یک بعدی

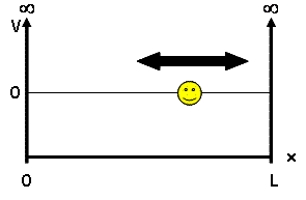
ذره‌ای را تصور کنید که در یک جعبه یک بعدی! (چاه پتانسیل ۱ بعدی) به طول $$L$$ به دام افتاده و نمی‌تواند از آن خارج شود. کف این جعبه دارای پتانسیل صفر و دیواره‌های آن به پتانسل بی‌نهایت متصل هستند (شکل 2).

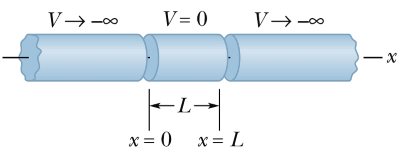
شاید تصویر زیر درک بهتری از مفهوم چاه پتانسیل یک بعدی را در ذهن شما حک کند. اگر یک سیلندر نازک (مثل سیم) نظیر یک خط را موجودی یک بعدی تصور کنیم، با تقسیم‌بندی آن به فرم شکل (۳) و با فرض اینکه تنها یک الکترون درون آن است، می‌توانیم الکترون مذکور را به دام اندازیم. علامت منفی در پتانسیل بی‌نهایت به این دلیل است که الکترون با بار منفی، جذب آن نشود.

در مقاله «معادله شرودینگر — به زبان ساده» با این معادله آشنا شدیم. با استفاده از این معادله می‌توانیم سطوح مختلف مجاز انرژی و تابع توزیع احتمال، که مربع قدر مطلق آن مکان ذره را نتیجه می‌دهد را به دست آوریم. در این مسئله نیز ابزار ما معادله شرودینگر بوده و از حل آن به اطلاعات مربوط به ذره درون چاه پتانسیل بی‌نهایت پی ‌می‌بریم.

نگران نباشید! حل این مسئله بسیار ساده بوده و کافی است به ترتیب زیر عمل کنید:

1. انرژی پتانسیل را متناسب با مسئله تعریف کنید. در اینجا داریم:

   $$V=\begin{cases}0 & 0<x<L\\\infty & Otherwise\end{cases}$$

2. با جایگذاری پتانسیل، معادله شرودینگر را می‌نویسیم. در اینجا پتانسیل درون ناحیه مد نظر ما، یعنی درون جعبه (چاه پتانسیل)، صفر است. پس داریم:

   $$\frac{-ℏ^2}{2m}\frac{d^2 ψ(x)}{dx^2}=Eψ(x)$$

3. معادله موج (در واقع همان معادله شرودینگر) را حل می‌کنیم. معمولاً پاسخ عمومی این دست از معادلات دیفرانسیل را از قبل می‌دانیم. در اینجا پاسخ معادله موج به صورت زیر است:

   $$ψ(x)=A\sin(kx)+B\cos(kx)$$

4. با استفاده شرایط مرزی در دیواره‌ها، پارامترهای موجود در تابع موج را به‌دست می‌آوریم. در اینجا شرایط مرزی متناسب با دو نقطه $$x=0$$ و $$x=L$$ ، یعنی طول جعبه (چاه پتانسیل) هستند. چرا که تابع موج در دیواره‌ها به دلیل پتانسیل بی‌نهایت آن‌ها صفر است.
5. تابع موج به دست آمده را در معادله موج شرودینگر گذاشته و $$E$$ را به دست می‌آوریم.

حل مسئله ذره در جعبه یک بعدی (چاه پتانسیل یک بعدی)

مطابق با روند فوق، معادله موج شرودینگر را متناسب با پتانسیل و شرایط مرزی مسئله مذکور حل می‌کنیم.

می‌دانیم که معادله شرودینگر به فرم زیر است:

$$\frac{-ℏ^2}{2m}\frac{d^2 ψ(x)}{dx^2}+V(x)ψ(x)=Eψ(x)$$
(1)

در مقاله «معادله شرودینگر — به زبان ساده» گفته شد که پاسخ معادله مذکور، معادله موج وابسته به ذره بوده که مربع اندازه آن، احتمال حضور ذره در آن مکان را نتیجه می‌دهد. یادآور می‌شویم که طبق رابطه دوبروی ($$\lambda=\frac{h}{p}$$) ، می‌توان به هر ذره با تکانه $$p$$ موجی با طول موج λ نسبت داد. در این مسئله ما به دنبال چگونگی رفتار ذره درون جعبه هستیم. چرا که با توجه پتانسیل تعریف شده، ذره در دیواره‌ها نمی‌تواند وجود داشته باشد. در واقع هیچ تابع موج وابسته به ذره‌ای در دیواره‌ها وجود ندارد. پس معادله شرودینگر برای ذره درون جعبه به فرم زیر در می‌آید:

$$\frac{-ℏ^2}{2m}\frac{d^2 ψ(x)}{dx^2}=Eψ(x)$$
(2)

پاسخ عمومی معادله دیفرانسیل فوق، به صورت زیر است که در آن $$A$$ و $$B$$ ثابت‌هایی هستند که از شرایط مرزی به دست می‌آیند.

$$ψ(x)=Asin(kx)+Bcos(kx)$$
(3)

شرایط مرزی در این مسئله، دو نقطه $$x=0$$ و $$x=L$$ هستند. همان طور که گفته شد، تابع موج در دیواره‌ها صفر است. شرط مرزی $$x=L$$ در اینجا کمکی به ما نمی‌کند. اما برای شرط مرزی $$x=0$$ داریم:

$$x=0 → ψ(0)=Asin(0)+Bcos(0)=0 ⇒B=0$$
(4)

برای اینکه تابع موج در دیواره $$x=0$$ صفر شود، ثابت $$B$$ باید صفر شود. پس تابع موج به صورت زیر در می‌آید:

$$ψ(x)=Asin(kx)$$
(5)

برای به دست آوردن $$k$$، به قرار زیر عمل می‌کنیم. در واقع قصد داریم با دوبار مشتق‌گیری و همانند‌سازی با معادله شرودینگر، $$k$$ یعنی بردار موج را به دست آوریم:

$$\frac{dψ(x)}{dx}=kAcos(kx)$$
(6)

$$\frac{d^2 ψ(x)}{dx^2}=-k^2 Asin(kx)$$
(7)

$$\frac{d^2 ψ(x)}{dx^2}=-k^2 ψ(x)$$
(8)

با جایگذاری در معادله شرودینگر نتیجه می‌شود:

$$\frac{-ℏ^2}{2m}(-k^2 ψ(x))=Eψ(x)$$
(9)

$$k=\sqrt{(2mE)/ℏ^2}$$
(10)

پس معادله موج وابسته به ذره به دام افتاده درون جعبه یک بعدی (چاه پتانسیل یک بعدی) به شکل زیر در می‌آید:

$$ψ(x)=Asin(\sqrt{ \left ( {(2mE)/ℏ^2 } \right ) } x)$$
(11)

توجه داشته باشید که در این روابط می‌توان از عبارت $$\hbar = \frac{h}{2\pi}$$ استفاده کرد. حال برای به دست آوردن ترازهای (سطوح) انرژی $$E$$ یک بار دیگر از شرایط مرزی استفاده می‌کنیم. استفاده از شرط $$x=0$$ در اینجا مفید نیست. چرا که کل معادله را صفر می‌کند. اما با استفاده از شرط $$x=L$$ داریم (معادله سینوسی در نقاط $$n\pi$$ صفر است):

$$x=L \rightarrow ψ(L)=Asin(ψ(x)=Asin(\sqrt{(2mE)/h^2}x)L)=0$$
(12)

$$\sqrt{(2mE)/h^2}L=n\pi$$
(13)

$$E=\frac{n^2 ℏ^2 }{2mL^2}$$
(14)

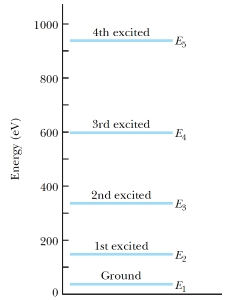
از آنجا که $$n$$ به صورت $$n=1,2,3,…$$ است، ذره هیچگاه نمی‌تواند در انرژی صفر باشد. در واقع تراز با انرژی صفر وجود نداشته و ذره همیشه مقداری انرژی جنبشی دارد. این امر طبق اصل عدم قطعیت هایزنبرگ در خصوص انرژی و زمان نیز صحیح است. چرا که طبق این اصل، اگر $$E$$ صفر باشد، ما زمان و مکان دقیق آن را می‌توانستیم مشخص کنیم. سطوح انرژی یک ذره فرضی در جعبه‌ای به طول $$L=100pm$$ در شکل (3) بر حسب الکترون ولت آورده شده است.

از معادله (13) نتیجه می‌شود که بردار موج $$k$$ برابر با ($$k=\sqrt{(2mE)/h^2}=\frac{n\pi}{L}$$) بوده و در نتیجه معادله موج به فرم ساده‌تر زیر در می‌آید:

$$\psi(x)=Asin(\frac{n\pi x}{L})$$
(15)

می‌دانیم که مربع قدر مطلق تابع موج، احتمال یافتن ذره را می‌دهد. بدیهی است که ذره در طول جعبه وجود دارد. پس احتمال حضور آن در جعبه برابر با یک است. در واقع می‌خواهیم با این کار (شرط نرمالیزاسیون) ضریب A را به دست آوریم:

$$∫_0^Lψ^2 (x)dx=1$$
(16)

$$A^2 ∫_0^Lsin^2 (nπx/L)dx=1$$
(17)

$$A=\sqrt{\frac{2}{L}}$$
(18)

در نهایت معادله موج وابسته به ذره به دام افتاده در جعبه یک بعدی به فرم زیر است:

$$\psi(x)=\sqrt{\frac{2}{L}}sin(\frac{nπx}{L})$$
(19)

نمودار تابع موج و احتمال حضور ذره

با مشخص بودن طول جعبه و با افزایش $$n$$ می‌توانیم به شکل موج وابسته به ذره در هر تراز پی ببریم. برای درک بهتر این امر، به شکل (۴) دقت کنید. این تصویر، شکل موج معادله (19) را به ازای $$n$$های متفاوت نشان می‌دهد.

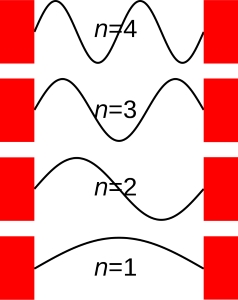
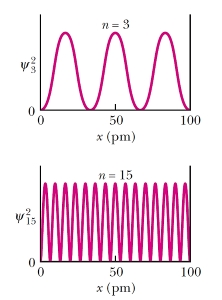
همچنین مربع قدر مطلق تابع موج که احتمال یافتن ذره را نتیجه می‌دهد برای $$n$$های متفاوت، به شکل زیر است. این نمودارها برای جعبه فرضی به طول $$L=100pm$$ رسم شده‌اند.

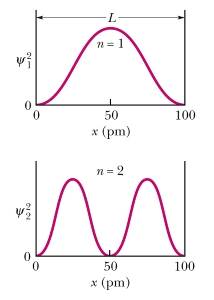
از  معادله (19) نتیجه می‌شود که با افزایش $$n$$، در واقع با افزایش انرژی، تعداد گره‌های فضایی یعنی مکان‌هایی که احتمال حضور ذره صفر است، افزایش می‌یابد. توجه داشته باشید در $$n$$های خیلی بزرگ، سطوح انرژی به یکدیگر نزدیک شده و همپوشانی می‌کنند و به صورت یک طیف پیوسته به نظر می‌آیند. در این حالت ذره شبیه به یک ذره آزاد رفتار کرده و می‌تواند هر انرژیی را اختیار کند. در انرژی‌های خیلی بالا می‌توان از قوانین مکانیک کلاسیکی استفاده کرد، چرا که ذره، رفتاری همچون موج پیوسته دارد. ذره در جعبه (چاه پتانسیل) می‌تواند مثالی از بحث دوگانگی موج – ذره باشد.

مولفه زمانی

در مقاله «معادله شرودینگر — به زبان ساده» دیدیم که اگر پتانسیل، ثابت و وابستگی زمانی نداشته باشد، می‌توانیم تابع موج ψ را به صورت حاصل‌ضرب قسمت مکانی و زمانی از روش جداسازی متغیر‌ها، یعنی به فرم زیر بنویسیم:

$$Ψ(x,t)=u(x)T(t)$$
(20)

همچنین دیدیم که با جداسازی متغیرها، قسمت زمانی معادله شرودینگر به فرم زیر در ‌می‌آید:

$$\begin{equation*} i\hbar\frac{\partial T}{\partial t} =ET \end{equation*}$$
(21)

پاسخ معادله دیفرانسیل فوق، به فرم ساده زیر است:

$$\large Ln(T)=\frac{-iEt}{\hbar} \rightarrow T=e^{\frac{-iEt}{\hbar}}$$
(22)

در بخش قبل، تابع موجی که به دست آوردیم (معادله 19) فقط قسمت مکانی را شامل می‌شد و نمودار‌های آن هیچ اطلاعاتی را در خصوص زمان به ما نمی‌دادند. طبق موارد گفته شده در بالا فرم کلی (مکانی و زمانی) معادله موج وابسته به ذره به صورت زیر در می‌آید:

$$\large Ψ(x,t)=\psi(x)e^{\frac{-iEt}{\hbar}}$$
(23)

دیدیم که انرژی به دست آمده وابسته به عدد $$n$$، یعنی کوانتیده است. انرژی به دست آمده ($$E=(n^2 ℏ^2)/(2mL^2 )$$) را می‌توانیم به صورت ($$E_{n}=n^{2}E_{1}$$) بنویسیم. پس معادله موج نهایی وابسته به ذره‌ای که در یک چاه پتانسیل بی‌نهایت به دام افتاده، از معادله‌های (19)، (22) و (23) به فرم زیر در‌ می‌آید:

$$\large Ψ(x,t)=\sum_n^∞ψ_n (x)e^{(-iEt)/ℏ}=\sqrt{\frac{2}{a}} \sum_n^∞sin⁡(\frac{n\pi x}{a})e^{(-i n^2 E_1 t)/ℏ}$$
(24)

جعبه با ابعاد بالاتر

حال فرض کنید که ذره در جعبه‌ای دو بعدی (چاه پتانسیل دو بعدی) به دام افتاده باشد. در این صورت ذره می‌تواند در دو راستای $$L_{x}$$ و $$L_{y}$$ حرکت کند. حرکت ذره در هر کدام از راستاهای $$L_{x}$$ و $$L_{y}$$ مشابه ذره در جعبه یک بعدی است. در واقع جعبه با ابعاد بالاتر تنها تعمیمی از حالت یک بعدی است. برای چاه پتانسیل دو بعدی، بردار موج $$k$$ به صورت زیر است:

$$k_{n_{x},n_{y}}=k_{n_{x}}x ̂+k_{n_{y}}y ̂=\frac{n_{x}\pi}{L_{x}}x ̂+\frac{n_{y}\pi}{L_{y}}y ̂$$

همچنین ترازهای انرژی و معادله موج به فرم زیر است:

$$E_{n_{x},n_{y}}=\frac{\hbar^{2}k_{n_{x},n_{y}}^2}{2m}$$

$$Ψ_{n_{x},n_{y}}=\psi_{n_{x}}(x,t,L_{x})\psi_{n_{y}}(y,t,L_{y})$$

شکل زیر تصویر تابع موج ذره‌ای به دام افتاده در چاه پتانسیل دو بعدی است که به ازای مقادیر $$n_{x}=4$$ و $$n_{y}=4$$ رسم شده است.

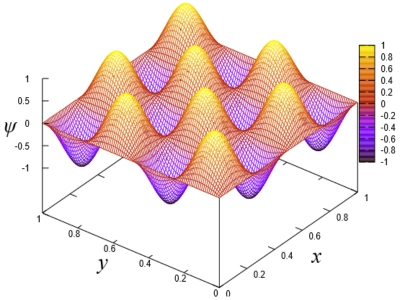
برای حالت ۳ بعدی نیز داریم:

$$k_{n_{x},n_{y}}=k_{n_{x}}x ̂+k_{n_{y}}y ̂+k_{n_{z}}z ̂=\frac{n_{x}\pi}{L_{x}}x ̂+\frac{n_{y}\pi}{L_{y}}y ̂++\frac{n_{z}\pi}{L_{z}}z ̂$$

$$E_{n_{x},n_{y},n_{z}}=\frac{\hbar^{2}k_{n_{x},n_{y},n_{z}}^2}{2m}$$

$$Ψ_{n_{x},n_{y},n_{z}}=\psi_{n_{x}}(x,t,L_{x})\psi_{n_{y}}(y,t,L_{y})\psi_{n_{z}}(z,t,L_{z})$$

مطلب فوق را می‌توان برای چاه پتانسیل $$n$$ بعدی نیز تعمیم داد. البته اگر در دنیایی با ابعاد بالاتر وجود داشته باشند.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک و ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های فیزیک
• آموزش مکانیک کوانتومی ۱
• مجموعه آموزش‌های ریاضیات
• عدم قطعیت هایزنبرگ — به زبان ساده
• کوانتوم — به زبان ساده
• درهم تنیدگی کوانتومی — به زبان ساده

^^